关于中学二次函数的解题策略

田 星 赵院娥

(延安大学数学与计算机科学学院，陕西 延安 716000)

函数的思想与方法的学习贯穿于整个中学数学教与学，其中，二次函数有着基础性的地位和作用，是学习其他函数知识的基石。并且以二次函数知识为主的综合性题目是中考的热点考题，在高中函数学习中也有重要的基础作用。本文就中学中有关二次函数的解题方法提几点有效策略。

一、中学生解决二次函数问题时的困难分析

(一)对于初中生来说，二次函数是初中学习中的重点与难点，初中生的思维发展水平限制了其对函数抽象性的理解，学生对于函数的概念并不理解，对于自变量与因变量之间的关系还处于疑惑阶段，只会死记硬背公式，定义也并不理解a，b，c的真实含义与三者之间的联系，因此在做题时便会遇到以下几个困难：

第一，学生很难准确找到自变量的取值范围，特别是隐含在题目中的限制条件；第二，在解决有关实际问题时，学生往往找不到题中等量关系不会建立数学模型；第三，对于数形结合，分类讨论等解题方法掌握不到位，找不到做题的最优解法。

(二)对于高中生来说，二次函数在高中函数学习中有着基础性的地位，是其他函数学习的基石，在考察中知识点的考查也越来越灵活，出题形式主要以综合试题为主。难度提升较为明显，对学生数学思维以及函数思想的要求也更高。二次函数在高中教学中要求学生通过观察、类比、归纳、分析、综合来建立严密的数学概念，掌握数学思想及方法，从而解决综合性问题。

二、中学解二次函数相关题型的几种方法

(一)数形结合法

数学本就是研究空间几何与数量关系的一门学科，在学习时数与形本就不可分。在解题时将待解决问题转化为与之等价的图形问题，不仅使问题直观化从而变得简单明了，而且可以加深学生对问题实质的理解。运用适当的数学思想及方法解决相关题型可消除学生解题障碍，提高学生解题兴趣。例如，二次函数中最值问题、单调性问题、求不等式解集等问题。

例1关于x的方程x2+2kx+3k=0的两根都在-1和3之间，求k的取值范围。

分析：由图像观察可知 令f(x)=x2+2kx+3k，

对应二次函数图像与横轴交点的坐标即f(x)=0的解，

要使符合已知条件，即需

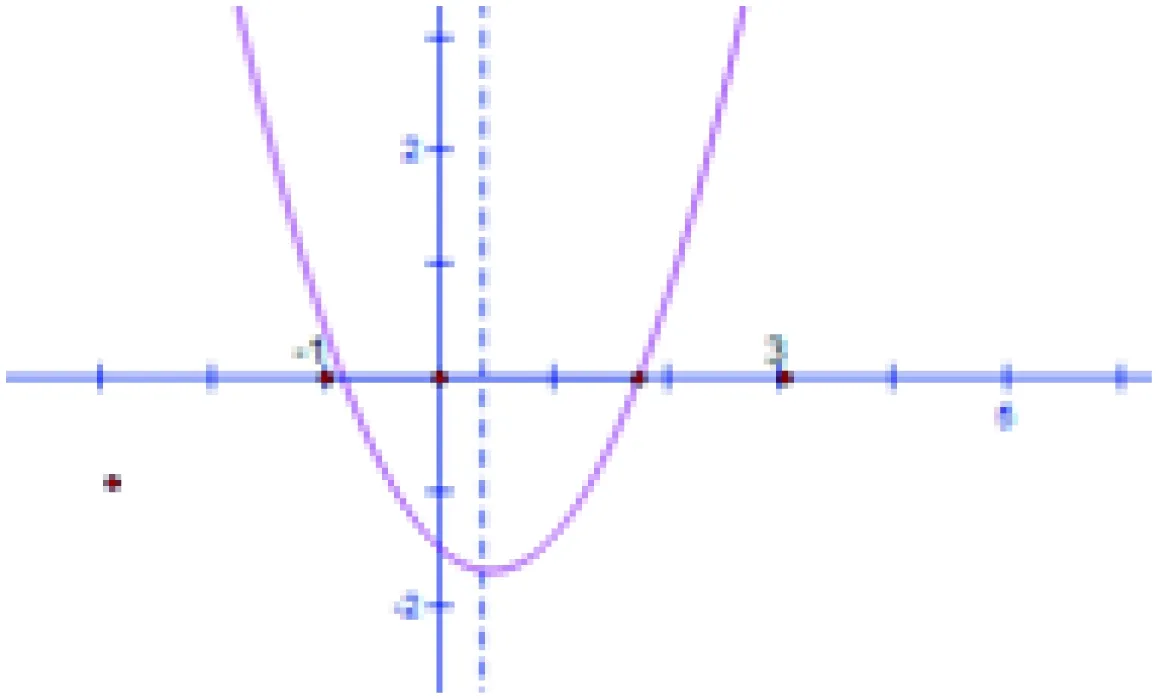
(二)转化法

应用转化法解二次函数题型时主要是将实际问题建立数学模型寻找等量关系，从而利用数学知识解答。不仅有利于解题，也有利于消除各学段学生对于二次函数学习时的障碍。

(三)分类讨论

分类讨论，解决问题时有关逻辑思维的数学思想，也是一种数学解题方法。其基本步骤“化整为零，各个击破，再积零为整”。是函数与其它知识点的综合考察时解题常用的一种方法。

例2解关于x的不等式x2-(a+a2)x+a3>0。

解：原不等式可化为(x-a)(x-a2)>0。

(1)a1或a<0)时，原二次不等式的解集为：{x│xa2}；

(2)当a>a2(0a或x

(3)当a=a2(a=0，a=1)时，原二次不等式的解集为：{x│x∈R且x≠a}.

注：因为a与a2大小不确定，所以需要讨论aa2，a=a2三种情况。

三、小结

二次函数知识的学习在初中或者高中都占据重要地位，因此探究二次函数的教学与解题是很有必要的，本文就常见几种解二次函数相关题型的方法做以阐述，希望可以帮助学生在解题时消除障碍，轻松作答。