冻土水力传导系数的理论模型研究

汤 瑞，周国庆，王建州，赵光思，焦 威



冻土水力传导系数的理论模型研究

汤 瑞，周国庆※，王建州，赵光思，焦 威

（中国矿业大学深部岩土力学与地下工程国家重点实验室，徐州 221008）

冻土水力传导系数多采用经验公式来描述，其结果缺少理论依据。该文从冰水界面水膜热力学理论出发，对克拉贝隆方程进行修正，得到孔隙水冻结温度与孔隙半径的关系式。基于此，结合毛细管束理论和土壤冻结特征曲线（SFCC），给出预测冻土水力传导系数的理论模型，并与前人的实测值和经验公式进行对比分析。结果表明：孔隙冻结温度随着孔隙半径的减小而下降，且温度下降速率也随之逐渐增大；考虑未冻孔隙水和未冻水膜作为水分的迁移通道，该模型计算值与试验结果具有很好吻合度，且优于经验公式，验证该模型的合理性；最后指出SFCC的拟合效果会影响该模型的预测结果。

冻土；水力传导系数；模型；孔隙大小；冻结温度；SFCC

0 引 言

全球陆地面积的70%分布着冻土，而中国多年和季节性冻土区总面积约占全国面积的75%[1]。随着中国重大工程的建设，如青藏铁路、输油管线、输配电等多年冻土及季节冻土区交通运输、水利电力、信息通讯、能源动力、民用工业建筑等大量冻土工程建设迅速发展，这些冻土工程建设势必受到冻土区土体冻胀的影响。而冻胀主要是水力梯度下的直接水分迁移和温度梯度等驱动下的水分间接迁移导致的冰分凝的宏观表现。冻土水力传导系数是影响未冻水迁移的主要因素之一。同时，在大量冻胀方程中，如水热耦合方程[2-4]、水热盐耦合方程[5-6]、水热力耦合方程[7-9]和水热盐力耦合方程[10-12]，从这些耦合方程中可知冻土水力传导系数是一项重要的模型参数。

对于冻土水力传导系数的研究国内外的学者做了大量的工作，并取得一定的成果。主要集中在两个方面：一是，通过试验装置直接测得冻土的水力传导系数[13-15]，如Watanabe等[16]实测在0 ℃附近处未冻水含量和冻土水力传导系数，结果表明当温度低于−0.5 ℃时，此时冻土不具有渗透性；同时测定了饱和冻土和非饱和未冻土的水力传导系数，并认为在相同含水量下两者的水力传导系数一致[17]；二是，采用间接的方法获得水力传导系数，并分为两类，一类是认为冻土的水力传导系数是仅关于温度的函数[18]，或是根据未冻土渗透系数预测公式，类比得到了冻土水力传导系数关于含冰量、含水量的函数[19]，另一类如Weigert等[20]通过分析冻结过程中水分分布间接估计冻土水力传导系数。但不管采用哪种方式得到的结果都不具有普适性，同时，预测方法的经验系数并没有明确的物理含义，也没有系数的确定步骤。所以采用经验公式得到的预测值，其合理性值得商榷。

鉴于冻土水力传导系数的理论研究较少，本文从土颗粒表面冰水界面水膜热力学理论出发，得到孔隙水冻结温度的表达形式。同时，结合毛细管束理论和SFCC给出预测冻土水力传导系数的理论模型。从理论上建立冻土水力传导系数与温度和未冻水含量之间的理论模型，可为冻胀模型研究提供重要的模型参数，亦可为寒区工程防冻胀问题提供参考和依据。

1 构建理论模型

1.1 孔隙冻结温度

针对正冻土冻结温度的研究，大量的学者都已验证了克拉贝隆方程的合理性。但该方程起初是以冰水溶液为研究对象，并认为冰和水的自由能仅受到温度和压力的影响。但在真实土体中孔隙水还受到土颗粒的吸力，这会导致孔隙水自由能下降，从而影响到孔隙水的冻结温度。基于此，周扬等[21]、胡坤[22]引入等效水压力对克拉贝隆方程进行修正，即

在冻结过程中不断变化，其中当180°时，冰点下降值最大。为了方便得到孔隙冻结温度随孔隙半径的变化，取180°，由公式（4）计算得图1。

图1 孔隙冻结温度与孔隙半径关系

从图1可以看出：孔隙冻结温度与半径存在依次对应，同时孔隙冻结温度随着半径减小而下降；孔隙半径在减小到10-6m时，孔隙冻结温度发生明显的变化，此时下降率开始明显增加。

1.2 基于毛细管束理论下未冻水体积含量

土体内部存在大小不一的孔隙，并被水和空气所占据。对于饱和未冻土，如图2a所示，为了方便研究未冻土的水力传导系数，前人假设土体中存在大小不一的毛细管束（如图2b所示），同时水分在毛细管中迁移。对于冻土，Stähli等[26]认为在冻土中孔隙被三相介质（空气、未冻水和冰）占据，其中未冻水存在于小孔隙中，空气存在于大孔隙中，而冰介于两者之间，并得到非饱和冻土的毛细管束模型。结合公式（4）可知：在冻结过程中，冰最先出现在孔隙半径较大的毛细管中。随着冻结温度不断的下降，孔隙水按照孔径从大到小依次相变成冰。换言之，在任何一个冻结温度下，都存在一个临界半径r，当毛细管孔径半径大于临界半径r，毛细管发生冻结；反之，毛细管未发生冻结。如图2c所示。

注：r为毛细管管径，ra为临界半径。

基于上述分析，假设冰为圆柱形并对称分布在毛细管中，管中水膜厚度处处相等，此时，未冻水含量包括以下两个部分：一是冻结孔隙中的未冻水膜，二是来自于未冻结孔隙的未冻水。故未冻水体积可表示为

式中V(r)表示半径为r的毛细管中未冻水的体积，N代表土体中毛细管的总数量；f(r)为土体中孔隙半径的概率密度函数；lr为实际的毛细管道的长度，m；如图3所示，并满足lr=ζ×l，其中l为直毛细管的长度，m；ζ为弯曲度（ζ≥1）。

在公式（5）中，右式中第一项表示未冻结毛细管中未冻水的体积含量，第二项为冻结毛细管中的未冻水膜的体积含量。假设研究的土体单元具有规则的形状如圆柱体或立方体，因此，土体单元的体积可以表示为

式中为土体试样的底面积，m2；为土体试样的高度，即为直毛细管的长度。利用公式（5）和公式（6），未冻水的体积含量可表示为

式7中，当土体的初始含水量确定时，r是定值；仅有r是随着冻结温度的下降而变化。将公式7对r求导得

1.3 基于毛细管束理论下冻土水力传导系数

同时毛细管断面上的速度分布满足边界条件，即在管壁处速度为零，得到毛细管中速度分布为

根据泊肃叶定律[27]，在半径为的单管管中，未冻水流量可以表示为

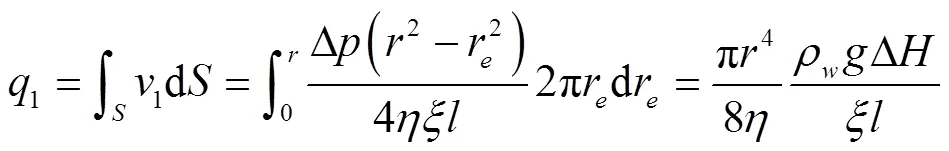
注：re为沿管径方向上的位置，v为流速，η为动力黏滞系数，τ为黏滞力。下同。

2）当r≤r<r时，毛细管中处于冻结状态，此时毛细管中存在冰和未冻水膜。由于在冰表面和管壁处流速为零，所以在半径-到中，存在一个半径1，在此处流速达到最大。故将未冻水膜划分为两个区域，如图5所示。

图5 冻结毛细管中流速分布

同理，流体满足力学平衡和边界条件（即，在冰水交界处和管壁处流速为零），故不同区域下流速分布的表达式分别为

式中2-1、2-2分别为图5区域1和2的流速分布。由于毛细管中流速是连续分布函数，故在1处2-1=2-2，故流速最大的位置为

在公式（15）中，右边第一项可以表示未冻土的总流量，第二项代表由于冰的生成而减小的流量。根据达西定律[27]，冻土的水力传导系数为

同理，在公式（16）中，右边第一项代表未冻土的水力传导系数，第二项表示是由于冰而导致水力传导系数下降值。可以看出该表达式能够表征冻土水力传导系数随温度的下降而减小的现象，且能够描述水力传导系数减小的过程。对公式（16）求导得

1.4 冻土水力传导系数预测模型

由于孔径的概率密度函数颇为复杂，极难用具体的数学形式来表述。为了规避该函数，利用公式（8）和公式（17），得到冻土水力传导系数与未冻水之间的关系

由公式（4）可知：r和关于温度的函数。为了计算推导方便，将上式简化为

对公式（19）从min到积分，可以得出冻土的水力传导系数。当积分上限温度min时，表明冻土中所有的毛细管都被冻结，此时冻土的水力传导系数为零。因此，冻水的水力传导系数表示为

式中T为参考温度，K；k为参考温度下冻土的水力传导系数，m/s。

2 本模型参数确定步骤

本模型需要的参数包括：最大孔隙的冻结温度max、最小孔隙的冻结温度min、未冻水含量关于温度的函数θ()、参考温度T和参考温度下的水力传导系数k，共计5个参数。其中参数取值如下：

1）θ()可通过对SFCC拟合得到；

2）对于max和min都是关于孔隙半径的函数，根据公式（4）可以获得。而最大和最小孔径需通过压汞试验确定。同时由于孔径概率密度存在差异，即使当大孔径发生冻结后，由于所占比重小，对水力传导系数影响不大。所以应该存在孔径阈值，当小于该阈值时冻土的水力传导系数会发生首次明显的变化。将孔径阈值所对应的温度近似定义为max。为了简化对max的确定过程，可通过SFCC的拟合公式获得：当未冻水含量等于初始含水量时，所得的温度即为max，并认为在0℃到max范围内未冻水含量不发生变化，水力传导系数也不发生变化。由1.2节内容可知：当纳米级的孔隙发生冻结时，较大孔隙都应发生冻结。而土体最小孔隙为纳米级，从图1中可以看出：纳米级的孔隙所对应的冻结温度为−45 ℃左右，即是min；

3）T和k可通过渗透试验获得。

3 验证与讨论

3.1 常用经验公式

Tarnawski等[28]提出冻土水力传导系数的预测公式，表达式如下：

式中k为饱和条件下未冻土的水力传导系数，m·s-1；为未冻水体积含量；饱和含水率；d为几何平均粒径；为几何方差；m、m和m分别为黏粒、粉粒和沙粒的质量分数；d、d和d分别为黏粒、粉粒和沙粒的粒径分布界限，其值分别为0.001、0.026和1.025 mm。

Fowler等[29]在O’Neill等[30]的基础上给出了预测冻土水力传导系数的经验公式

然而，Lundin[31]认为冰的产生是导致冻土水力传导系数下降的原因，冻土的水力传导系数应等于同等液量下未冻土的水力传导系数乘以与含冰量有关的阻抗因子，并给出了相应的预测公式

3.2 算例分析

根据文献[32]，试样为青藏粉质黏土，其基本物理参数见表1所示。

表1 青藏粉质黏土的基本物理参数

7） 本模型参数

张虎等[32]通过试验得到冻结特征曲线，并根据实测数据拟合得到未冻水与温度之间关系，如图6所示。在图6中，实测数据点分布在−0.3～−5 ℃之间，温度为0 ℃时对应试样的初始含水量，而阴影面积为未冻水的“黑盒子”，该范围内未冻水的变化是未知的。

图6 部分拟合的SFCC

根据第2节内容，确定本模型参数，取-0.3℃为参考温度。本模型具体计算参数见表2。并根据已有的拟合公式得到完整的冻结特征曲线，如图7所示。

表2 本模型计算参数

注：θuw为未冻水含量，T为土体温度。下同。

Note: θuwis the unfrozen water content, T is the soil temperature. The same as below.

注：Tmax为最大孔隙的冻结温度。

2）结果分析

将上述3中预测公式计算结果和本文理论模型以及实测数据相互对比，如图8所示。

图8 水力传导系数模型与经验公式和实测值比较

从图8中可以看出：由4种方法所预测的冻土水力传导系数随温度变化的趋势基本一致，且都满足随温度的下降而减小的规律。但通过Tarnawski公式[28]和Lundin公式[31]所得的预测值与实际观测值存在较大的偏差，偏差量甚至超过4个数量级。仅本模型和Fowler公式[29]表现良好，当温度低于−0.4 ℃时，Fowler公式[29]所得的预测值要更加接近实测值，但该预测公式中存在经验系数，其值往往是从某一范围中任意确定，并没有明确的物理意义和取值步骤，其预测值的可靠性值得商榷。而本模型的计算值大多接近实际观测值，仅在0～−0.0357 ℃范围内存在差异，但曲线整体逼近实测值。同时，本模型中所有参数都要明确的物理意义，故优于其他的经验公式。

4 结 论

本文建立了冻土水力传导系数的理论模型，并和前人的试验数据以及常用的经验公式进行对比分析，研究表明：

1）本模型计算结果和试验结果有很好的吻合度，验证本模型的合理性，且本模型不存在经验系数，要优于其他的经验公式，具有普适性。故本模型建议采用SFCC来计算冻土水力传导系数的观点。

2）将毛细管束运用到冻土中，考虑未冻水膜和孔隙水两个迁移路径，能够很好的揭示水分迁移过程。在基于水膜热力学理论，考虑土颗粒吸力对未冻水膜化学式能的影响，得到修正后的克拉贝隆方程，使得孔隙冻结温度的表达式更加合理。其中，孔隙冻结温度随着孔隙半径的减小而下降。

3）本模型是基于准稳态过程而提出的，由于在0 ℃附近冻土处于剧烈的相变阶段，为了减弱该影响，所以不能采用部分SFCC，应使用更加精确完整的SFCC。

[1] 周幼吾，郭东信，邱国庆，等. 中国冻土[M]. 北京：科学出版社，2000.

[2] Harlan R L. Analysis of coupled heat-fluid transport in partially frozen soil[J]. Water Resource Research, 1973, 9(5): 1314－1323.

[3] 汪仁和，李栋伟.正冻土中水热耦合数学模型及有限元数值模拟[J]. 煤炭学报，2006(6)：757－760.

Wang Renhe, Li Dongwei. Moisture-temperature coupling mathematical model in freezing soil and finite element numerical simulation[J]. Journal of China Coal Society, 2006(6): 757－760. (in Chinese with English abstract)

[4] Wu Daoyong, Lai Yuanming, Zhang Mingyi. Heat and mass transfer effects of ice growth mechanisms in a fully saturated soil[J]. International Journal of Heat and Mass transfer, 2015, 86(1): 699－709.

[5] 黄兴法，曾德超，练国平.土壤水热盐运动模型的建立与初步验证[J]. 农业工程学报，1997，13(3)：37－41.

Huang Xingfa, Zeng Dechao, Lian Guoping. A numerical model for coupling movement of water heat and salt in soil under the conditions of frozen, unfrozen, saturated and unsaturated[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1997, 13(3): 37－41. (in Chinese with English abstract)

[6] Padilla F, Villeneuve J P. Modeling and experimental studies of frost heave including solute effects[J]. Cold Regions Science and Technology, 1992, 20(2): 183－194.

[7] 刘月，王正中，王羿，等. 考虑水分迁移及相变对温度场影响的渠道冻胀模型[J]. 农业工程学报，2016，32(17)：83－88.

Liu Yue, Wang Zhengzhong, Wang Yi, et al. Frost heave model of canal considering influence of moisture migration and phase transformation on temperature field[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(17): 83－88. (in Chinese with English abstract)

[8] Liu Zhen, Yu Xiong. Coupled thermo-hydro-mechanical model for porous materials under frost action: Theory and implementation[J]. Acta Geotechnica, 2011, 6(2): 51－65.

[9] Zhou Jiazuo, Li Dongqing. Numerical analysis of coupled water, heat and stress in saturated freezing soil[J]. Cold Regions Science and Technology, 2012, 72(3): 43－47.

[10] Wu Daoyong, Lai Yuanming, Zhang Mingyi. Thermo- hydro-salt-mechanical coupled model for saturated porous media based on crystallization kinetics[J]. Cold Regions Science and Technology, 2017, 133(1): 94－107.

[11] 冯瑞玲，蔡晓宇，吴立坚，等.硫酸盐渍土水-盐-热-力四场耦合理论模型[J]. 中国公路学报，2017，30(2)：1－10，40.

Feng Ruiling, Cai Xiaoyu, Wu Lijian,et al. Theoretical model on coupling process of moisture-salt-heat-stress field in sulfate salty soil[J]. China Journal of Highway and Transport, 2017, 30(2): 1－10, 40. (in Chinese with English abstract)

[12] 牛玺荣. 硫酸盐渍土地区路基水、热、盐、力四场耦合机理及数值模拟研究[D]. 西安：长安大学，2006.

Niu Xirong. The Study and Numerical Simulation on Moisture-Heat-Salt-Stress Coupled Mechanism in the Sulphate Saline Soil Subgrade[D]. Xi'an: Chang'an University, 2006. (in Chinese with English abstract)

[13] Burt T P, Williams P J. Measurement of hydraulic conductivity of frozen soils[J]. Canadian Geotechnical Journal, 1974, 11(4): 647－650.

[14] Burt T P, Williams P J. Hydraulic conductivity in frozen soils[J]. Earth Surface Processes, 1976, 1(4): 349－360.

[15] Horiguchi K, Miller R D. Hydraulic conductivity functions of frozen materials[C]//Proc. 4th Int. Conf. Permafrost, National Academy Press, Washington D C, 1983: 504－508.

[16] Watanabe Kunio, Osada Yurie. Simultaneous measurement of unfrozen water content and hydraulic conductivity of partially frozen soil near 0 °C[J]. Cold Regions Science and Technology, 2017, 142(10): 79－84.

[17] Watanabe Kunio, Osada Yurie. Comparison of hydraulic conductivity in frozen saturated and unfrozen unsaturated soils[J]. Vadose Zone Journal, 2016, 15(5): 1－7.

[18] Nixon J F D. Discrete ice lens theory for frost heave in soils[J]. Canadian Geotechnical Journal, 1991, 28(6): 843－859.

[19] Taylor G S, Luthin J N. A model for coupled heat and moisture transfer during soil freezing[J]. Canadian Geotechnical Journal, 1978, 15(4): 548－555.

[20] Weigert A, Schmidt J. Water transport under winter conditions[J]. Catena, 2005, 64(2): 193－208.

[21] 周扬，周国庆，周金生，等. 饱和土冻结透镜体生长过程水热耦合分析[J]. 岩土工程学报，2010，32(4)：578－585.

Zhou Yang, Zhou Guoqing, Zhou Jinsheng, et al. Ice lens growth process involving coupled moisture and heat transfer during freezing of saturated soil[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(4): 578－585. (in Chinese with English abstract)

[22] 胡坤. 冻土水热耦合分离冰冻胀模型的发展[D]. 徐州：中国矿业大学，2011.

Hu Kun. Development of Separated Ice Model Coupled Heat and Moisture Transfer in Freezing Soils[D]. Xuzhou: China University of Mining and Technology, 2011. (in Chinese with English abstract)

[23] Scherer G W. Crystallization in pores[J]. Cement and Concrete Research, 1999, 29(8): 1347－1358.

[24] Israelachvili J N. Intermolecular and Surface Forces-intermolecular and Surface Forces[M]. London: Academic Press, 1991.

[25] Dash J G, Fu H, Wettlaufer J S. The premelting of ice and its environmental consequences[J]. Report on Progress in Physics, 1995, 58(1): 115－167.

[26] Stähli M, Jansson P E, Lundin L C. Soil moisture redistribution and infiltration in frozen sandy soils[J]. Water Resources Research, 1999, 35(1): 95－103.

[27] 李广信. 高等土力学[M]. 北京：清华大学出版社，2011.

[28] Tarnawski V R, Wagner B. On the prediction of hydraulic conductivity of frozen soils[J]. Canadian Geotechnical Journal, 1996, 33(1): 176－180.

[29] Fowler A C, Krantz W B. A generalized secondary frost heave model[J]. SIAM Journal on Applied Mathematics. 1994, 54(6): 1650－1675.

[30] O’Neill K. The physics of mathematical frost heave models: A review[J]. Cold Regions Science and Technology, 1983, 6(3): 275－291.

[31] Lundin L C. Hydraulic properties in an operational model of frozen soil[J]. Journal of Hydrology, 1990, 118(4): 289－310.

[32] 张虎，张建明，张致龙，等. 冻结状态青藏粉质黏土的渗透系数测量研究[J]. 岩土工程学报，2016，38(6)：1030－1035.

Zhang Hu, Zhang Jianming, Zhang Zhilong, et al. Measurement of hydraulic conductivity of Qinghai-Tibet Plateau silty clay under subfreezing temperatures[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(6): 1030－1035. (in Chinese with English abstract)

[33] Brooks R H, Corey A T. Properties of porous media affecting fluid flow[J]. Journal of the Irrigation and Drainage Division, 1966, 92(2): 61－90.

Research on theoretical model for hydraulic conductivity in frozen soils

Tang Rui, Zhou Guoqing※, Wang Jianzhou, Zhao Guangsi, Jiao Wei

(,221008)

The hydraulic conductivity of frozen soil is not only one of the main factors affecting the speed of moisture migration, but also an important model parameter in a large number of frost heave models. However, the study of the hydraulic conductivity for frozen soil is often described by empirical formulas. The calculation results lack a theoretical basis, and the predicted values of different empirical formulas often have enormous deviations. Therefore, it is debatable to use the empirical formula to predict the hydraulic conductivity coefficient of frozen soil. In order to reveal the process of moisture migration, according to the theory of water film thermodynamics at the ice-water interface, this paper points out that the water flow can be regarded as the Darcy flow under the equivalent pressure control in frozen soil. On this basis, the expression of pore water freezing temperature and pore radius is obtained. The capillary bundle theory is applied to the frozen soil and combined with the soil frozen characteristic curve to give a theoretical model for predicting the hydraulic conductivity of frozen soil, Meanwhile, the function of pore radius probability density is eliminated to make this proposed model convenience to calculate and use. The calculated values of this model are compared with the experimental data and empirical formulas of the predecessors. The results show that the pore freezing temperature decreases with the decrease of pore radius, and the temperature drop rate also increases. The freezing temperature reduction rate is significantly accelerated especially when the pore radius is less than 10-6m. Considering the unfrozen pore water and the unfrozen water film as the migration channel of moisture, in general, the calculated values of this model agree well with the experimental results and are better than the empirical formula, which proves the rationality of the model. The predicted values of the hydraulic conductivity of frozen soil obtained by three empirical formulas are even different by four orders of magnitude for Qinghai-Tibet silty clay. Although the predicted value obtained by the Fowler formula is closer to the measured value, there is an empirical coefficient in the prediction formula. For the empirical coefficient is often arbitrarily determined in a certain range, and it is no clear physical meaning and calculation procedure, which leads to the reliability of the predicted value from the empirical formula is debatable. At the same time, the power function is used to fit the soil frozen characteristic curve (SFCC) in this model, which tends to infinity near 0 ℃. In order to ensure the continuity of the function of the SFCC, the piecewise function is used to describe the soil frozen characteristic curve, but the deviation of the calculated and measured values of the model within 0−-0.035 7 ℃. Because the model is based on a quasi-steady state process, and the frozen soil is in the stage of intense phase change near 0 ℃. Thus, this paper pointed out that the fitting formula of the soil frozen characteristic curve is very important to this model for reducing this deviation near 0 ℃.

frozen soils; hydraulic conductivity; models; pore size; freezing temperature; SFCC

汤 瑞，周国庆，王建州，赵光思，焦 威. 冻土水力传导系数的理论模型研究[J]. 农业工程学报，2019，35(4)：138－144. doi：10.11975/j.issn.1002-6819.2019.04.017 http://www.tcsae.org

Tang Rui, Zhou Guoqing, Wang Jianzhou, Zhao Guangsi, Jiao Wei. Research on theoretical model for hydraulic conductivity in frozen soils[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(4): 138－144. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.04.017 http://www.tcsae.org

2018-07-31

2019-02-19

国家自然科学基金面上项目（NO.41672343，NO.41772338）；国家自然基金（NO.51204164）

汤 瑞，博士生，从事冻土物理学及寒区工程等方面研究。 Email：tangrui19920210@163.com

周国庆，教授，博士生导师，从事冻土物理学、力学与工程方面研究。Email：gqz@cumt.edu.cn

10.11975/j.issn.1002-6819.2019.04.017

S152; TU47

A

1002-6819(2019)-04-0138-07