基于异质网络的蜂拥控制研究
张金春,丛 凯,王帅磊
(海军航空大学, 山东 烟台 264001)
蜂拥行为是指蜂群、鱼群、鸟群等生物群体利用简单的几条规则和环境信息,通过个体之间的相互影响,最终形成稳定有秩序的群体运动[1-7]。1987年,Reynolds[8]提出了具有代表性的蜂拥控制三条规则:分离、聚合和速度匹配。后来,Olfati-Saber[9]也对蜂拥控制算法改进和优化。现在,蜂拥控制已经在无线传感器网络、机器人编队、无人机等各领域应用。1995年,Vicsek等[10]提出了均质感知模型:在二维平面上,存在一群初始位置随机分布的质点,它们的运动速率相同但是运动方向随机分布,并且感知半径相同。因为质点的感知半径相同,所以称为均质感知模型。对于任意一个质点,它下一时刻的运动方向受到其感知半径内其他质点的运动影响。
在实际生活中,很多智能体系统应该是异质的,即智能体的影响半径各不相同。比如在生物群体中因为年龄和权威等个体差异使得每个个体对其他个体的影响能力各不相同。近年关于异质多智能体的研究中,文献[11]在“跟随者-领导者”的框架下,分别针对有外界干扰和存在多个虚拟领导者的情况,在异质多智能体系统中研究如何设计不同的控制策略使跟随者能够很好地跟踪领导者。文献[12]研究了异质多智能体系统的分组一致性,推导出了异质多智能体系统实现分组一致性的充分条件。文献[13]研究了混合类型多智能体组成的异质多智能体系统的组一致性问题,得出了通信延迟与分组一致性无关的结论。本文主要研究当智能体系统异质时,异质性的强弱对于多智能体系统最终蜂拥状态的影响。
1 蜂拥控制
1.1 预备知识
在二维平面上,假设存在n个智能体,全部视为质点。第i个智能体的运动方程为:
(1)
其中:qi∈Rn为第i个智能体的位置;pi∈Rn为速度;ui∈Rn为加速度,也就是控制输入。
对于智能体i,在任意时刻t,将它感知半径内的所有智能体的集合记为Ni(t)={j|||qi-qj||≤r2,j∈N且j≠i},其中,||·||为欧几里得范数,r为感知半径,称Ni(t)为智能体i的邻居。把智能体i视为节点,将它与其他能感知到的节点用无向边连接,则由系统内所有节点和无向边组成的网络构成了一个无向图G(t)。其邻接矩阵为A(G(t))=[aij(t)],其中
(2)
幂律分布最早由Zipf发现,他发现英文单词的出现频率与其序号的常数次幂存在反比关系:
P(r)=r-α
(3)
本研究中,智能体的影响半径服从幂律分布。
1.2 传统蜂拥控制模型
1986年,Reynolds[9]提出了一种蜂拥控制模型,并提出了三条规则:分离、聚合、速度匹配。根据Reynolds提出的模型,Olfati-Saber[10]提出了如下控制输入算法:
(4)
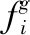
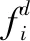
▽qiψα(|||qij-qγij||σ)
(5)
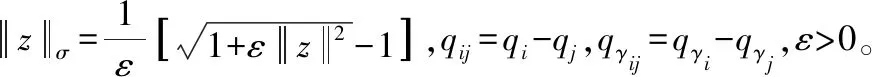
φα(z)=ρh(z/rα)·φ(z-dα)
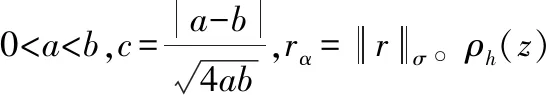
(6)
控制输入ui的具体形式为:
hi[c1(qγ-qi)+c2(pγ-pi)+uγ]
(7)
这里,hi可以用来描述智能体i是否拥有领导者的引导信息。当hi=1时,智能体i为信息智能体,当hi=0时,智能体为自由智能体。
人工势函数ψα(z)满足:① 当||qij||σ→0时,ψα为最大值;② 当||qij||σ趋近于某一期望值时,ψα为最小值;③ 当||qij||σ≥||r||σ时,ψα恒为很小的正常数。人工势函数ψα如图1所示。
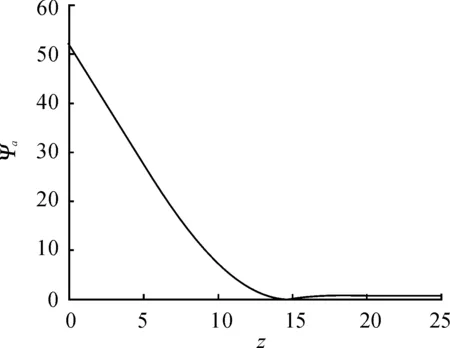
图1 人工势函数
1.3 影响半径服从幂律分布的蜂拥控制算法
在Reynold和Olfati-Saber等提出的蜂拥控制算法中,ri表示的是智能体的感知半径,即智能体i能够感知到感知半径ri内的其他邻居的位置信息和速度信息,影响自己的控制输入。但是在智能体系统异质时,感知半径的概念无法表达智能体的影响能力,所以本文将ri重新定义为智能体i的影响半径,即智能体i能够将自己的位置信息和速度信息传递给影响半径ri内的其他智能体。当智能体系统均质时,感知半径和影响半径的意义相同,但是当智能体系统异质时,感知半径和影响半径的不同会对结果产生不同的影响,所以要对控制输入进行改造。
当智能体系统异质时,智能体i是否能够接收到智能体j的信息取决于智能体j的影响半径,所以新的邻居定义如下:
且j≠i}
新的邻接矩阵定义如下:
(8)
当智能体系统均质时,邻接矩阵是对称阵;当智能体系统异质时,因为影响半径不相同,所以邻接矩阵不是对称阵。
除了邻居和邻接矩阵,异质网络对于势能函数也会产生影响。对于碰撞函数式(6),因为影响半径不同,所以自变量应该替换为z/||rj||σ,而不是z/||r||σ。
最后,因为本文主要研究在异质网络下多智能体系统的自主演化行为,所以本文不研究带有领导者的蜂拥控制输入,因为领导者具有全局信息,所以无论初始分布如何,最终肯定能够形成稳定的蜂拥行为。在对邻居、邻接矩阵和碰撞函数进行改造以后,新的控制输入如下:
其中,c3为系数,主要影响智能体之间的分离聚合作用,c3=0.25。
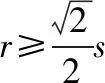
其中,xmin为系数,用以保证ri>d。
当幂律指数变化时,生成的智能体影响半径分布也会发生变化。图2是当s=55时不同幂律指数对应的影响半径分布图。
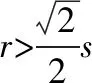
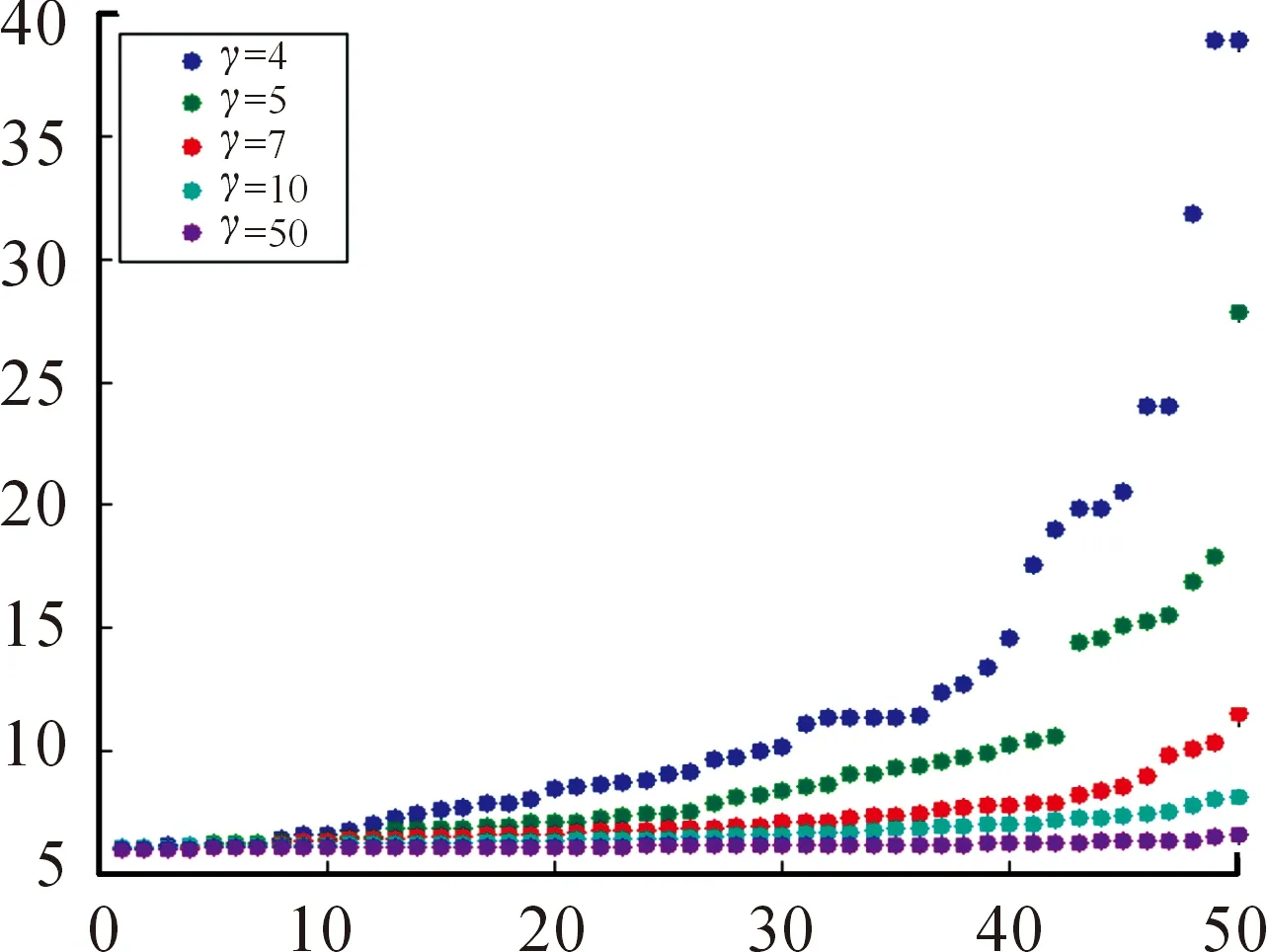
图2 不同幂律指数下的影响半径分布
2 仿真结果与分析
本研究模仿了50个智能体在二维平面中的运动情况。参数分别设置为:智能体初始速度为[-1,1]和[-1,1],初始分布范围为[0,55]和[0,55],智能体最小影响半径xmin=6,智能体间期望距离d=5,σ范数的参数ε=0.1,式(8)中参数h=0.9,φ(z)中a=1,b=2,控制输入中c1=0.1,c2=0.9,c3=0.25,程序运行步数loop=300。为了更好地体现不同影响半径下智能体之间的相互影响,本文不要求智能体的初始分布必须为初始连通。通过计算机数值仿真验证当幂律系数分别等于γ1=4,γ2=5,γ3=7,γ4=10,γ5=50对智能体系统蜂拥状态好坏和收敛速度的影响。
首先本文对γ1=4时的智能体系统进行了数值仿真,研究系统随程序运行时的演化过程。
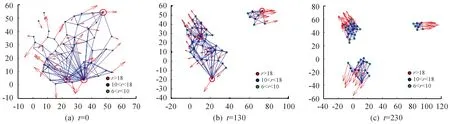
图3(a)是智能体的初始分布图。从图中可以看出智能体的速度是随机分布的,网络的连通性也不强,其中有3个影响半径r>18的智能体,因为影响半径较大的原因,所以它们对其他智能体的运动有较强的引导作用,它们可以充当“中心智能体”的作用。当t=50时,可以看出所有影响半径较小的智能体都受到几个影响半径较大的智能体的影响,向中心智能体运动。当t=100和t=150时,智能体已经基本完成了Reynolds提出的三条规则中的分离聚合作用,开始按照同一方向开始运动。当t=300时,所有智能体已经形成了稳定的α-晶格结构,并且在几个中心智能体的影响下按照同一方向进行运动,形成了稳定的蜂拥状态。
通过对上图的分析可知,当幂律指数较小时,智能体系统中存在极少数影响半径极大的智能体,它们可以充当“中心智能体”甚至“领导者”的作用,它们的速度和位置会对其他影响半径较小的智能体产生决定性的作用,最终蜂拥状态的好坏取决于极少数中心智能体的初始分布状态。
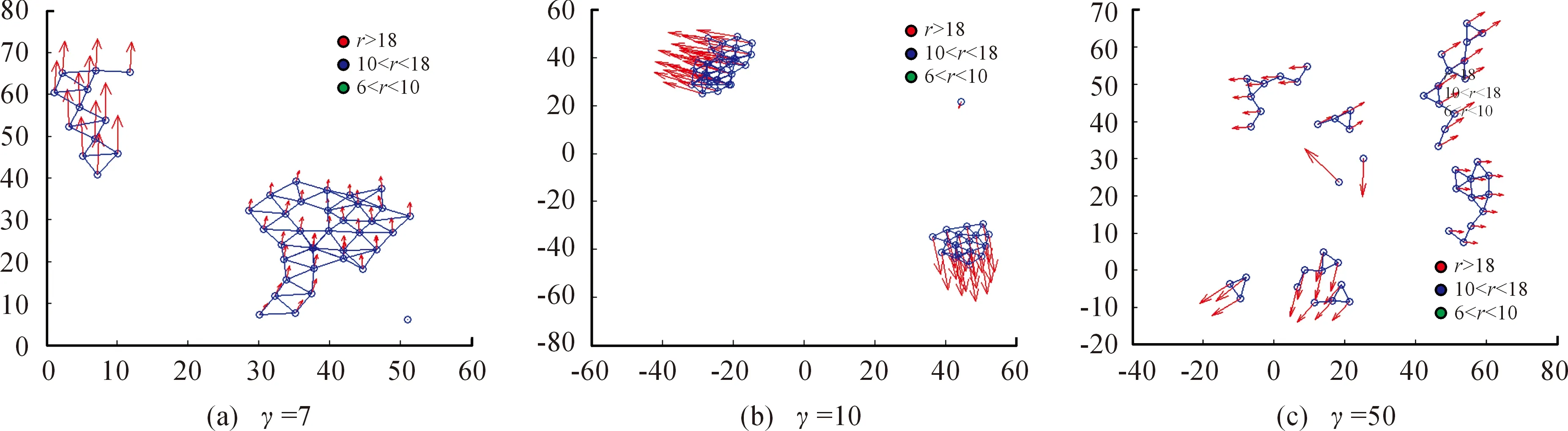
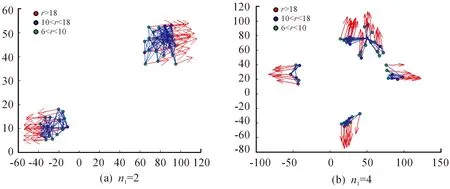
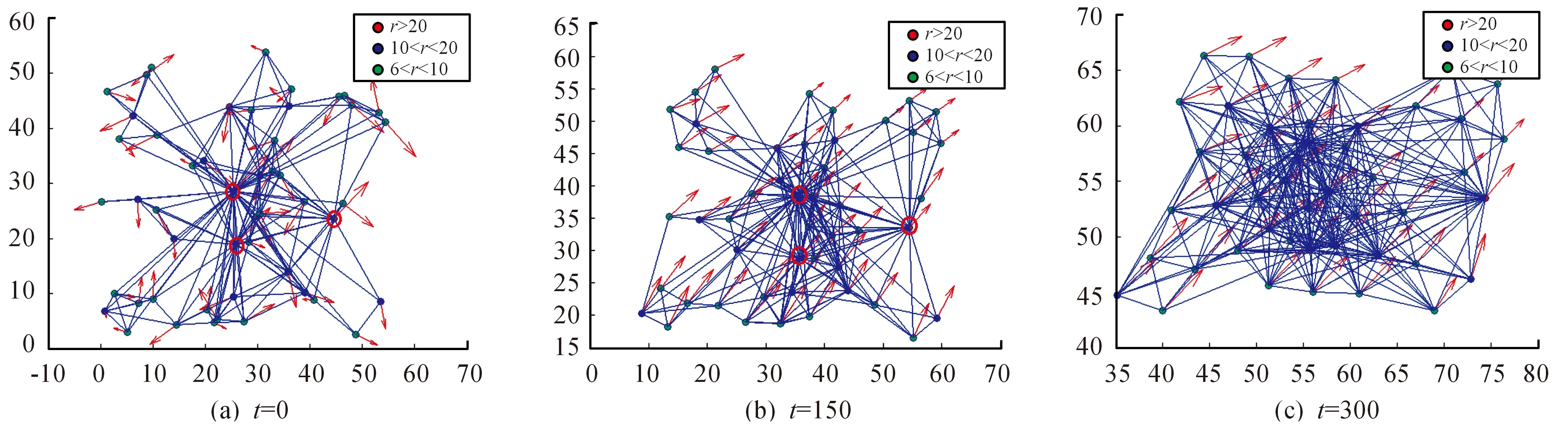
下面比较当幂律指数分别取γ1=4,γ2=5,γ3=7,γ4=10,γ5=50时对智能体系统的影响,每种情况分别取10次实验数据取平均值。本文采用最大簇系数S来判断蜂拥状态的好坏,S为智能体节点网络中所有连通子图中最大连通子图的智能体个数与所有智能体个数的比值,0 从图4可以看出,当幂律指数较小时,智能体系统的初始最大簇系数比较大,这是因为系统中存在少数中心智能体,以这些中心智能体为节点更容易形成连通网络;相反当幂律指数较小时,所有智能体的影响半径都比较小,所以很难形成节点很多的连通网络。 随着程序运行,可以看出幂律指数较小的最大簇系数增长更快,这是因为中心智能体影响半径更大,更容易影响其他智能体。并且可以明显看出,幂律指数不同会对最后的最大簇系数产生很大的影响:当γ1=4,γ2=5,γ3=7,γ4=10,γ5=50时,s1=0.97,s2=0.844,s3=0.742,s4=0.624,s5=0.364。当幂律指数较小时,最大簇系数很大,收敛时间也更短,系统的蜂拥状态也更好;当幂律指数较大时,最大簇系数很小,收敛时间更长。这说明当系统的异质性很强时,多数智能体在极少部分中心智能体的带领下,更容易形成整体的蜂拥状态;随着异质性逐渐减弱,智能体变得更加均质,在运动过程中容易受到部分影响半径较大的智能体的影响,形成“分块”或者“分离”现象,如图5所示。从图5能够看出,随着异质性减弱,影响半径越来越小,导致智能体的分离现象也更加明显。 根据前面的数值仿真可知,当系统异质性很强时,智能体的运动主要受到极少部分中心智能体的影响,最终蜂拥状态的好坏取决于中心智能体的运动状态。接下来本文重点研究,在系统的异质性很强的条件下,中心智能体的运动状态对智能体系统运动的影响,以及能否通过对极少部分的中心智能体施加控制,达到对整个智能体系统进行控制,最终形成统一的蜂拥运动。为了保证系统的异质性,接下来研究的内容中幂律指数γ=4。 为了对智能体进行分类,本文设定影响半径r>20的智能体称为控制智能体,影响半径6≤r≤20的智能体称为一般智能体。在运动过程中,设控制智能体保持匀速直线运动,则对于控制智能体来说ui=0,对所有智能体来说,控制输入为: 图5 不同幂律指数对应的分离现象 图6 n1=3时不同时刻智能体分布 通过上面分析可知,在异质性较强的智能体系统中,极少数影响半径很大的控制智能体的运动状态可以影响其他所有智能体的运动,当这些控制智能体的运动方向不相同时,会对其影响半径之内的其他智能体产生影响,最终会形成稳定的分块式的蜂拥运动,并且影响半径越大,形成的分块也越大。接下来本文研究能否通过控制极少数中心智能体,让它们按照同一方向运动,进而达到控制所有智能体的运动,最终形成稳定的蜂拥运动。设所有影响半径r>20的控制智能体的速度都为(1,1),控制输入ui=0,则所有控制智能体都按照同一速度进行匀速直线运动。 从图8可以看出,t=0时,智能体的初始分布比较散乱;t=100时,所有智能体都能达到同一运动方向;t=300时,能够形成比较紧凑的α-晶体结构。这样就说明了在异质性较强的智能体系统中,即使初始分布随机性很强,但是通过控制极少数控制智能体按照同一方向运动,就可以牵制绝大多数其他智能体,最终形成稳定的蜂拥运动。 图7 n1=2,4时形成的分块式的蜂拥运动 图8 同一方向运动时的智能体蜂拥运动图 1) 本研究提出了基于异质网络的蜂拥控制算法。 2) 对势能函数进行了改造,并且通过数值仿真证明了异质性较强的智能体系统更容易达到蜂拥状态,并且证明了可以通过控制极少数影响半径较大的智能体控制整个智能体系统,使其达到预定的蜂拥状态。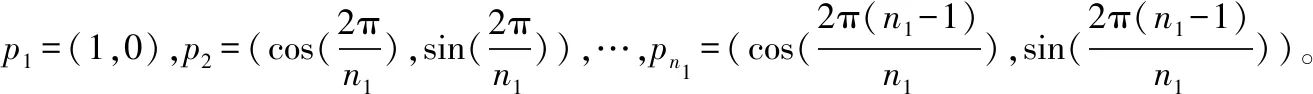
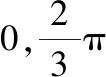
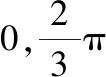
3 结论

