基于改进Huber-M的组合导航鲁棒滤波算法

王进达,鲁 浩,程海彬,李群生

(中航工业空空导弹研究院， 河南 洛阳 471009)

提高SINS/GNSS紧组合导航系统的鲁棒性是当前导航领域的研究热点[1]。在紧组合的弹载应用中，大过载、高机动以及卫星缺失等复杂条件经常出现，这使得紧组合必须具备很好的鲁棒特性和状态跟踪特性。

目前提高组合导航滤波器鲁棒性的方法主要集中在线性/非线性滤波算法框架内进行时间更新或量测更新的改进。如H∞滤波器[2]、自适应滤波器[3-4]和抗差Kalman滤波器[5]，其中H∞滤波器是基于放宽噪声容限来对未知噪声进行范围估计，自适应滤波器是直接将未知噪声统计量作为状态量进行估计的，抗差Kalman是在传统Kalman基础上对未知噪声方差矩阵进行等效替换。三者是鲁棒线性滤波框架的代表。非线性滤波框架内的鲁棒改进更是广泛，基于贝叶斯理论基础的容积卡尔曼滤波、粒子滤波、扩展卡尔曼滤波以及无迹卡尔曼滤波等[6]，其中容积卡尔曼算法(Cubature Kalman Filters，CKF)是较新的非线性滤波算法。

基于鲁棒滤波器的改进，目前应用较多的是在CKF框架内引入强跟踪机制(Strong Tracking Filters, STF)，并在此基础上进行多种简化[7-10]。而传统STF的关键是如何准确地确定渐消因子，并且渐消因子的引入条件具有一定的随机性，导致滤波结果不够稳定，出现误判概率过高的现象[11]。而引入Huber-M估计[12]虽然能够解决这个问题，但是目前大多数基于Huber-M估计的鲁棒滤波算法应用在目标跟踪领域中[13-15]，在导航领域应用较少。

GNSS/SINS紧组合导航系统在高动态条件下其非线性特性表现明显，此时采用线性框架下的鲁棒滤波器已不再适用。因此，本文提出一种基于改进Huber-M估计的CKF导航算法。对Huber-M估计进行改进，应用于非线性的导航系统观测方程，不进行线性近似，保持了CKF在方差传递过程中原有的精度；其次，并不直接通过Huber条件下的最小二乘迭代得到状态估计，而是利用Huber估计出新的量测噪声方差矩阵对一步预测协方差矩阵进行二次正交化处理，既能提高系统鲁棒性，又可避免噪声方差矩阵的变化可能导致的模型不确定性；最后引入强跟踪机制，采用模糊推理方式计算弱化因子，保证量测噪声统计特性发生突变或状态突变时，系统滤波器仍能够对导航系统姿态误差实现良好跟踪。

1 基于改进Huber-M估计的容积卡尔曼滤波

1.1 Huber-M估计与强跟踪机制的统一

关于状态量xk和m维观测量yk建立非线性系统模型如下：

(1)

式(1)中，f(·)和h(·)分别为非线性状态函数和量测函数；vk和wk分别为状态噪声和量测噪声，其方差矩阵分别为Qk和Rk。

广义M估计的Huber代价函数的定义如下：

(2)

式(2)中，ρ(υi)为关于υi的任意函数；υi为观测残差。由此可以得到式(2)的解为：

(3)

式(3)中，φ(υi)=(ρ(υi))′，影响函数为ψ(υi)=φ(υi)/υi。

构造Huber条件下的回归模型，假设状态一步预测残差为δxk+1/k，于是有

(4)

根据Huber原理和式(2)定义新的残差及代价函数，如式(5)、式(6)所示：

(5)

(6)

(7)

从式(7)可以看出，Huber-M估计的关键是构造伪观测值或重新构造观测噪声方差矩阵，将原非线性观测值截断，从而定义修正后的残差。这样做的好处是能够自适应地对不同大小的残差配以权重，减小量测异常的影响。引入正交原理来使得滤波器输出的残差序列处处正交，能够进一步减小观测噪声方差矩阵的变化对状态方程的影响。

在SINS/GNSS紧组合数学模型中，由于量测方程的非线性特性，采用线性滤波框架下的强跟踪机制会造成系统模型失配，导致滤波迭代的不稳定，因此需要避免对观测方程进行线性化。强跟踪算法中渐消因子的计算如下：

λk=max(1,λ0)

(8)

(9)

(10)

(11)

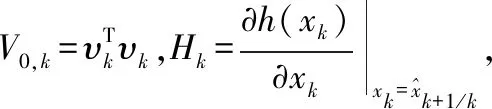
(12)

(13)

1.2 弱化因子的求解

在式(10)、式(11)中β′>1为弱化因子，取值通常靠经验选取，其作用是使状态估计值更加平滑，但取值过大，会明显增加量测噪声矩阵对渐消因子选取的影响，人为地调节弱化因子不仅降低了对动态条件下状态平滑的作用，还增加了滤波发散的风险。对此，本文采用模糊逻辑对弱化因子的取值进行改进，在强跟踪原理的基础上，建立模糊规则，从而避免人为因素的影响。

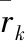
(14)

(15)

式(14)中，υk,i为新息第i个分量。输入输出采用平滑度更好的高斯型隶属函数，如图1所示。

图1 输入输出的高斯型隶属函数

设定该模糊系统的模糊子集合为{A,B,C}={Z(0),S(小),L(大)}，则根据T-S模型可制定模糊规则如表1所示。

表1 模糊规则

根据表1的模糊规则，可采用重心法进行解模糊求出弱化因子。

1.3 改进的Huber-M STCKF算法步骤

通过1.1节～1.2节的分析和计算，可以得到基于改进Huber-M估计的强跟踪容积卡尔曼滤波算法步骤如下。

步骤1：时间更新，计算容积卡尔曼滤波的容积点[17]；

步骤3：根据模糊原理得出弱化因子，求渐消因子λk+1；

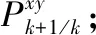
步骤7：计算滤波增益、状态估计值与预测方差。

2 基于伪距-伪距率差的紧组合模型

设定组合导航系统的状态方程如下：

(16)

式(16)中，X=[φxφyφzδVEδVNδVUδLδλδhΔtdΔtv]T，各状态量依次为失准角、速度误差、位置误差、接收机钟差和钟漂。系统状态矩阵的定义如下：

(17)

式(17)中，Fij(i,j=1,2,3)的具体定义可参见文献[16]，FG为GNSS误差方程的状态驱动矩阵。

由于接收机钟差的时间导数为钟漂项，那么采用钟差项δtd和钟漂项δtv作为状态量的GNSS误差方程为：

(18)

式(18)中，Tc为相关时间系数；ωd、ωv分别为噪声项。因此有

量测模型为：

下面推导包括伪距和伪距率差的非线性观测方程，假设惯导给出的ECEF系下的导航系统位置为(xI,yI,zI)，卫星定位组件共跟踪k颗卫星，其中第i颗卫星在ECEF系下的位置是(xSi,ySi,zSi)，则相应于惯导给出的导航系统位置到第i颗卫星的伪距观测差为：

(19)

式(19)中，(δx,δy,δz)为惯导给出的导航系统在地球坐标系中的位置误差。其与状态量中的位置参数之间的关系为：

(20)

那么式(20)减去第i颗卫星观测到的伪距值，可以得到关于伪距差的非线性模型为:

δρi=ρIi-ρGi=

(21)

式(21)中，ρ为卫星与接收机之间的理想伪距；w1i为观测噪声。

式(20)与式(21)组成GNSS/SINS紧组合导航系统的双差非线性量测模型。

3 仿真验证

本文导航坐标系采用东-北-天当地地理坐标系。假设导航系统初始位置为北纬34.2°，东经108.9°，高度380 m；初始速度为340 m/s。传感器采样周期为0.01 s，滤波周期0.1 s；陀螺常值漂移为3°/h，加速度常值误差为0.1 mg，GNSS随机伪距率误差为0.05 m/s，进行165 s的仿真时间，飞行轨迹包括加速、爬升、转弯等机动过程，如图2所示。

无量测异常条件下，常用的滤波算法能够保持较好的导航精度，因此本文只考虑有量测异常情况下所提出算法的导航精度和鲁棒特性。选用传统KF(Kalman Filter)算法、ACKF(Adaptive Cubature Kalman Filter)算法和本文提出的Huber-STCKF三种方法的导航结果进行对比。设置量测异常，在t=80～120 s设置量测噪声方差为初始状态的1.2倍，并将其设置为状态突变。

图2 导航系统运动轨迹

考虑三种方法的导航精度，其三种方法的姿态误差角与速度误差分别如图3、图4所示。

图3 量测异常条件下3种方法的姿态误差角对比

图4 量测异常条件下3种方法的速度误差对比

从图3可以看出，当出现量测异常时，3种方法x和y向失准角估计值在量测异常后能够保持稳定，而z轴失准角除本文方法外的两种方法均出现了不同程度的发散现象，滤波器此时无法保证稳态精度。导致这种现象的原因是前两种方法对量测异常过于敏感，导致在滤波估计过程中增益矩阵跟随异常值发生突变，使得滤波器对状态量无法保持收敛，而本文提出的方法因为强跟踪机制的引入使得系统同时能够保证滤波新息的正交化，也就是说能够最大限度的提取异常量测量中的有用信息并进行滤波更新，具有较高的鲁棒性能。

同样，在图4的速度误差估计也能够看出，东向和天向的速度误差相差不大，而北向速度误差则在量测异常时出现不同程度的发散现象。说明速度分量在系统模型中三种方法的非线性度相似，而北向速度误差在量测异常时导致模型非线性特性增强，导致AKF和KF方法均出现精度下降现象，而本文的Huber-M STCKF则能够较好地保持导航精度。

对该条件进行50次蒙特卡罗仿真，对比三种方法的失准角和速度误差大小，如表2所示。可以明显看出，本文提出的鲁棒估计算法导航精度均高于ACKF和KF算法。

表2 本文方法与其他方法的估计误差比较

总的来说，量测异常的出现导致三种算法对姿态误差的估计精度都会有所下降，但本文提出的方法能够较好地保持估计精度。这是由于在量测异常发生时，由Huber-M估计出的噪声方差矩阵发生同步变化，并且强跟踪机制的引入能够对量测信息突变保持较高的鲁棒性能。

4 结论

基于改进Huber-M估计的容积卡尔曼滤波导航算法(Huber-STCKF)通过将Huber-M估计应用于非线性的导航系统观测方程，避免了非线性模型的线性化；引入强跟踪机制，利用新的量测噪声方差矩阵对一步预测协方差矩阵进行正交化处理，采用模糊推理方式计算弱化因子，提高了系统的鲁棒性。通过仿真验证，与传统卡尔曼滤波算法(KF)和自适应容积卡尔曼滤波算法(CKF)进行对比，新的算法在量测异常条件下具有更好的鲁棒性、更高估计精度，能够对导航系统姿态误差实现良好的跟踪性。