动车组车辆车下悬吊设备线路振动特征分析

杨 军

(中国铁路北京局集团有限公司车辆处，100860，北京//高级工程师)

0 引言

铁道车辆多体动力学系统会存在刚柔耦合振动，比较典型的是车体的结构振动及其与其它连接结构的耦合作用。高速列车弹性振动最突出的例子就是动车组车体的低频弹性振动和高频结构噪声，其中车体低频弹性振动主要是与车下设备的耦合振动。国内外很多学者对此展开了研究，文献[1]考虑了车体的弹性，计算了车体的动态响应。文献[2]通过考虑车体弹性，计算了弹性车体对于旅客舒适度的影响。文献[3]建立了客车垂向振动模型，计算了客车系统幅频特性曲线；对有和无动力吸振器的客车系统进行了随机振动分析，分析结果表明，动力吸振器能够抑制车体某些频率成分，适当增大吸振器质量、刚度和阻尼可以达到良好的减振效果。文献[4]考虑车体弹性响应后，将车体考虑为等截面欧拉梁，二系悬挂考虑为半主动悬挂；考虑车体的一阶和二阶弹性模态，车体一阶弯曲自振频率应避开构架的浮沉自振频率，由于车体弹性的影响，车体端部振动大于车体中部。文献[5]采用刚柔耦合模型计算了动车组垂向传递规律。文献[6]采用动力吸振器来抑制车体的弹性振动，优化设计的动力吸振器可以有效控制车体弹性振动，而且动力吸振器的质量越大，减振性能越好；当动力吸振器的质量为1 000 kg、车体垂向一阶弯曲频率低至6.5 Hz时，对于时速达250 km的高速客车仍可实现优良的运行品质。文献[7—8]研究了采用压电元件后的车体弹性振动。文献[9]考虑车体弹性，建立车辆轨道耦合垂向模型，计算了车体弹性振动动力学响应及悬挂设计时考虑的因素。文献[10]计算和比较分析了考虑车下设备和未考虑车下设备时的车体模态。文献[11—12]采用刚柔耦合模型计算了车体弹性振动对于车下设备振动的影响。

本文首先介绍了车下悬吊设备的质量调谐吸振理论，随后通过国内某高速动车组实测数据，分析了正常线路和蛇形激励线路两种工况下的动车组车下设备的振动状况，以及运行速度和运营里程对车下悬吊设备的影响。

1 高速动车组车辆车下悬吊设备质量调谐吸振理论

1.1 车下悬吊设备

目前常见的车下设备主要包括高频磁致振动设备、旋转件设备、大质量设备和其他无源设备几类，如图1所示。

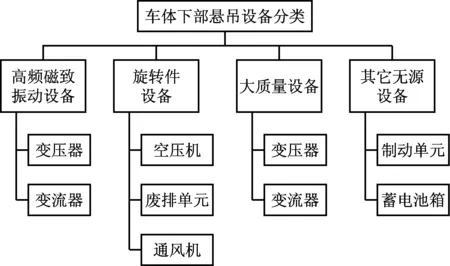
图1 动车组车下悬吊设备分类

1.2 质量调谐吸振理论

根据弹性梁车体模型与设备垂向耦合振动关系，结合弹性系统的动力消振的力学模型，将车体与设备耦合振动模型简化为弹性体和离散质量构成的混合动力学系统，如图2所示。可以应用动力吸振理论来匹配车下设备和弹性车体的模态，以最大程度抑制车体的弹性振动，提高车体的弹性模态。

图2 车体与设备耦合振动模型

JACQUOT R G用模态分析、模态截断和模态综合法给出一般弹性构件动力吸振的近似解法。对于均直弹性梁而言，如果只考虑它的第一主振型，相当于求解主质量为M的单自由度振动系统受集中力激励时的动力吸振问题。均直梁的动力吸振采用离散振动系统幅频特性方法，用模态截断法和模态综合法可导出全系统的运动方程，进而可得广义坐标x1对广义力的动力放大系数，那么安装动力吸振器后，动力放大系数等于主质量为M的单自由度系统动力吸振的动力放大系数。式(1)为主质量计算公式。

(1)

式中：

M——弹性车体质量；

ρ——单位长度密度；

A——车体截面面积；

l——车体长度；

Y1(a)——弹性梁第一阶振型函数。

式(1)表明，若将动力吸振器安装在车体振动幅值最大位置，则可使其主质量M最小。相对于确定的吸振器质量m，质量比μ=m/M将取得最大值，因此能获得最好的吸振效果。式(2)为均直梁动力吸振器的最优悬挂频率比计算公式。

(2)

式中：

fopt——设备最优悬挂频率比(车体一阶弯曲频率)。

根据均直梁的自由振动微分方程可推导其振型函数，结合自由梁的边界约束条件，可得其频率方程及固有频率方程。

自由梁固有频率方程：

λi=(2n+1)π/2

(3)

根据自由梁的振动微分方程，可得弹性均直梁的振型函数为：

Yi(x)=coshβix+cosβix-A(sinhβix+sinβix)

(4)

其中，A=(coshλix-cosλix)/(sinhλix-sinλix),βi=λi/l

式中：

βi——为阵型系数。

1.3 吊挂刚度设计准则

在动车组车下设备吊挂刚度设计中，主要将设备分为A、B、C三类，三类设备设计采用不同的设计准则，具体分类如下：

(1)A类设备：为有源设备，垂向悬挂频率为7 Hz左右，基于隔振理论设计。横向悬挂频率为垂向的0.5～0.7倍左右，纵向悬挂频率为垂向的3倍左右。

(2)B类设备：为无源大质量设备，垂向悬挂频率为9 Hz左右，基于质量调谐吸振理论设计，采用动力学和有限元优化。横向悬挂频率为垂向的0.7～1.0倍左右，纵向悬挂频率为垂向的3倍左右。

(3)C类设备：为无源小质量设备，垂向悬挂频率为10～11 Hz左右，基于垂向简化梁模型的动力吸振理论设计，并考虑连接可靠性。横向悬挂频率为垂向的0.7～1.0倍左右，纵向悬挂频率为垂向的3倍左右。

2 试验过程

基于350 km/h动车组线路长期服役动力学性能跟踪试验，分析车下设备振动特征。给出不同转向架运动状态下的设备、车体的横向、垂向加速度，分析其频谱组成，并对振动源进行分析。

列车持续以350 km/h最高速度运行，车轮磨耗里程约为20万km。构架加速度采样频率为2 kHz，选用带通滤波器对构架加速度振动频率进行0.5～12.0 Hz的滤波。车下设备加速度数据采样频率为1 kH，选用带通滤波器对车下设备加速度振动频率进行0.1～200.0 Hz的滤波。

选取设备有、无显著弹性振动时段数据进行分析，分析局部时段内的设备与车体连接处的车体测点、设备测点的横向、垂向振动加速度，对比时域、频域信号特征，总结设备的线路振动动态响应特征。

分析典型车下设备部件辅助变流器等设备的线路振动特征，给出对应路段的转向架横向稳定性分析结果。主要分析设备、车体在有、无蛇形激励振动时的时域和频谱特征。

3 试验结果分析

为了探究车体弹性振动对于车下设备振动的影响，分别截取了正常路段和弹性振动显著路段数据，分别对比了构架振动响应、车下设备振动响应，以及车速和线路对车下设备振动特性的影响。

3.1 构架振动响应

图3和图4中分别为正常路段和蛇形激励路段构架端部横向加速度时域图和频域图。

a) 时域图

b) 频域图

a) 时域图

b) 频域图

由图3、图4可见，时域图中，正常路段构架横向加速度较小，最大值为0.2g；蛇形激励路段构架出现明显的谐波振动，构架横向加速度最大值为0.4g左右。通过频域图可以看出，正常路段构架横向加速度振动值较小，在一个较宽的频带上；而弹性显著路段构架横向振动主频为7.4 Hz，横向加速度振动幅值为0.2g。

3.2 车下设备振动频响分析

在振动水平正常时段，选取振动水平较低时段数据进行分析，如图5、图6所示。选取变流器数据进行分析：设备横向、垂向加速度振动幅值为0.2g，并且横向、垂向振动水平相同；车体横向、垂向加速度振动幅值为0.05g，并且横向、垂向振动水平相同。由分析可知，设备振动显著大于车体振动；设备频域振动特征主要为高频磁致振动，频域波形显示主频为100 Hz；设备15 Hz以上的高频振动均未传递至车体，即弹性元件有效隔离了设备激扰向车体的传递；主频0.6 Hz、1.6 Hz对应车体刚体模态；辅助变流器的垂向悬挂模态对应的主频约为8.8 Hz，车体结构模态对应的主频约为9.2 Hz，附近频带较宽。

a)横向振动

b)垂向振动

a)横向振动

b)垂向振动

选取转向架蛇行激励时段数据进行分析，如图7、图8所示。设备横向、垂向加速度幅值约为0.3g和0.2g，即弹性振动时其横向振动水平大于垂向振动水平；车体横向、垂向加速度幅值均约为0.1g；转向架蛇行激励时段，对应的弹性振动幅值显著大于刚体运动幅值；设备频域振动特征主要为高频磁致振动，设备15 Hz以上的高频振动均未传递至车体，即弹性元件有效隔离了设备激扰向车体的传递；主频0.6 Hz、1.6 Hz对应车体刚体模态；转向架蛇行激励时段，辅助变流器和车体耦合振动频率为7.6 Hz；设备和车体振动相位基本相同。

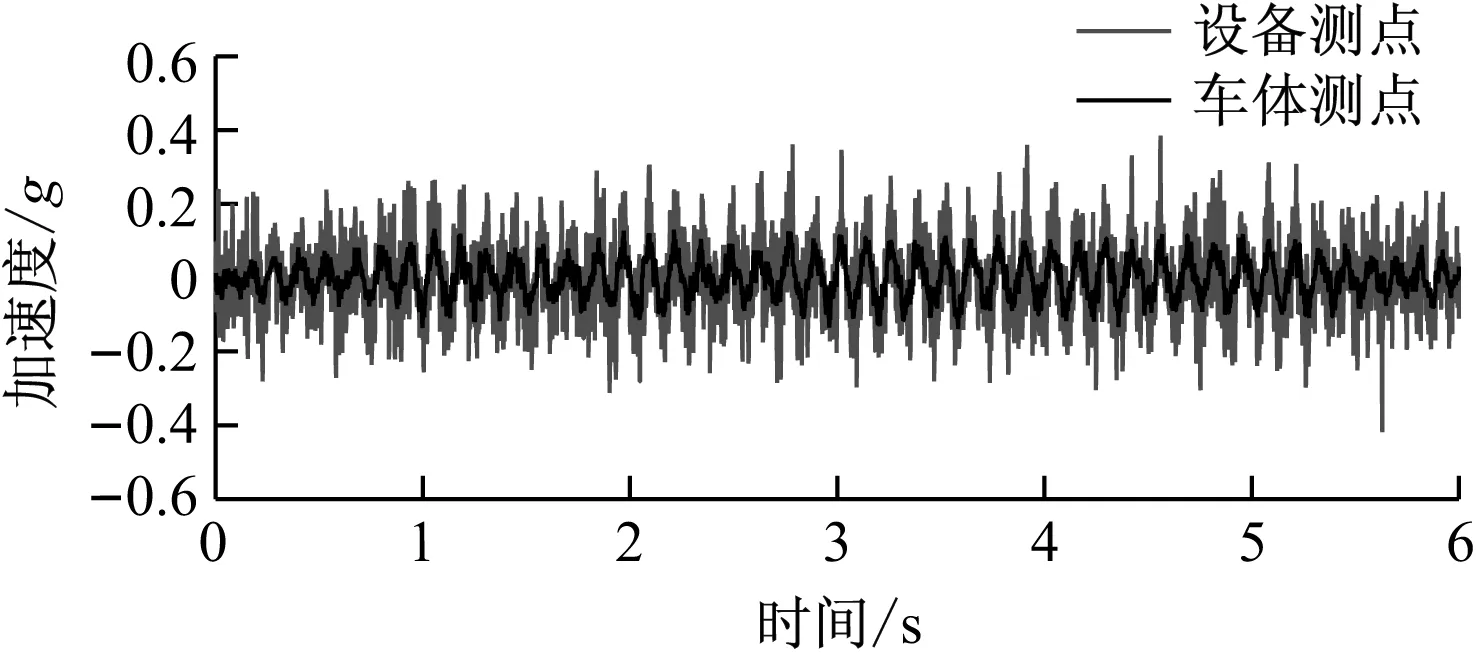
a)横向振动

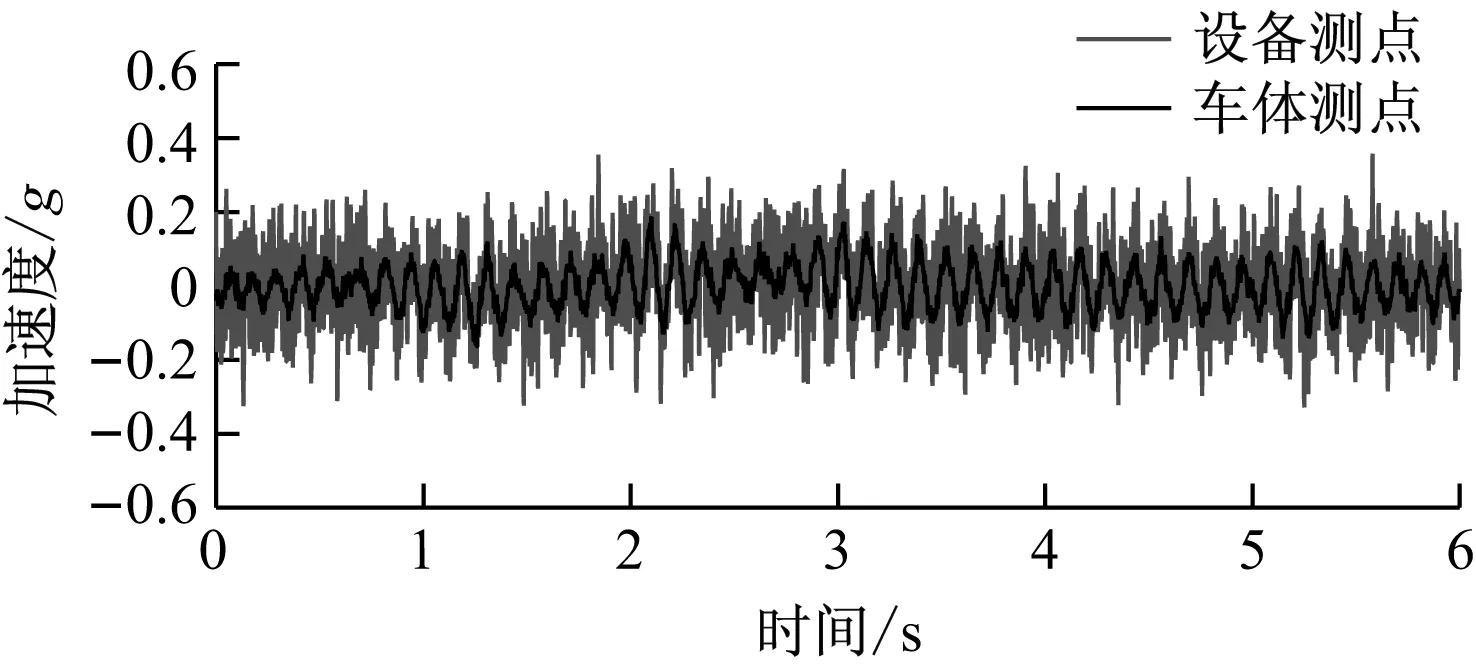
b)垂向振动

a)横向振动

b)垂向振动

3.3 列车运行速度对车下设备振动的影响

列车运行速度对车下设备振动的影响如图9所示。车体与车下设备(枕梁、车体底架、裙板、车下设备等)振动数据显示，当列车运行速度在380 km/h及其以上时，车体与车下设备的振动水平高于350 km/h时的振动水平。当速度为350 km/h时，其横向振动加速度小于300 km/h和380 km/h的。垂向加速度随着速度的增大不断增大。

3.4 线路对车下设备振动的影响

车体变流器吊挂点在不同线路上的振动加速度如图10所示。

a)牵引变流器前左上方车体横向加速度

b)牵引变流器前左上方车体垂向加速度

a)车体变流器吊挂点横向加速度

b)车体变流器吊挂点垂向加速度

由图10可见，在线路1横向振动加速度量级约为0.20～0.25g，线路2横向振动加速度量级为0.25g，线路3的横向振动加速度量级为0.18g。列车在线路3上的振动状态好于在线路1和线路2上的。列车在线路1和线路2上的横向振动加速度数据离散性大，轴箱在哈大线上的横向振动加速度比在大西线和郑徐线大上的大。在线路3上，横向振动加速度数据较为集中，但相对来说在线路2上时振动加速度最大。

4 结论

本文通过对高速动车组车体和车下设备耦合振动理论分析，对试验数据进行分析，可以得出以下结论：

(1)在正常路段，构架横向振动加速度振动幅值较小，在一个较宽的频带上；而在蛇形激励路段，构架横向振动主频为7.4 Hz，横向振动加速度振动幅值为0.2 g。

(2)在振动水平正常时段，设备振动显著大于车体；设备频域振动特征主要为高频磁致振动；设备15 Hz以上的高频振动均未传递至车体。转向架蛇行激励时段，辅助变流器和车体耦合振动频率为7.6 Hz，设备和车体振动相位基本相同。

(3)随着运营速度增大，车下设备振动逐渐增强。

(4)在不同线路上，车下设备振动状态不同，线路3上好于线路1和线路2。