基于平衡抛射原理的火箭筒内弹道仿真研究

边朝阳，姚养无，刘 怡

(中北大学 机电工程学院，山西 太原 030051)

现代战争要求地面部队有一定的防空、反坦克及打击坚固目标的能力，一次性使用的各类单兵火箭武器具有体积小、质量轻、便于携带和使用，并且具备破甲、攻坚、杀伤和燃烧多种功能，能够有效对付战场上的坦克、装甲车辆和野战工事等目标，使其成为许多国家陆军常规武器中不占编制的标准配备[1]。传统单兵火箭武器发射时易产生的发射冲击波、后抛堵片、高温燃气射流及射流吹起的沙砾等对射手安全构成威胁[2]。因此一种具有“有限空间内发射”能力的单兵火箭武器应运而生，它采用了平衡抛射原理，在发射时具有微光、微声和微焰(烟)等“三微”特征，且后坐力与后喷危险界限小，是未来单兵火箭武器的发展方向[3]。因此，研究平衡抛射火箭武器的内弹道特性并进行验证试验，可为平衡抛射原理的应用推广提供理论指导。

1 平衡抛射火箭武器的工作原理

某型单兵火箭武器采用平衡抛射原理，也称戴维斯原理，是利用发射时向后抛出与火箭弹同样质量的配重体抵消后坐力，使发射管不产生后坐运动的一种发射原理。整个发射系统由火箭弹、平衡体、前/后活塞(以火箭弹飞出方向为前，下同)、前/后变形环、高强度玻璃钢发射筒和击发传火机构等部件组成，是一种全封闭式平衡抛射装置，如图1所示[4]。

发射时首先打开保险，扣动扳机后击针击发底火，底火产生的燃气通过传火管进入发射筒中间位置的发射药管，被点燃的发射药在筒内瞬间燃烧产生高温高压燃气，前/后活塞受高温高压燃气影响瞬间产生微小形变而与筒壁紧密贴合保证气密性，同时燃气压力继续升高，超过药管的抗拉强度后药管从中间断开。然后前/后活塞在燃气作用下分别推动弹丸和平衡体向前、后筒口运动。同时到达筒口后前/后活塞冲击前/后变形环，前/后活塞的运动瞬间停止，火箭弹和平衡体靠惯性与前后活塞脱离后继续飞行，火箭弹最终飞向目标。由于平衡体由一定数量的薄塑料片组成，被抛出后，在空气阻力作用下，速度急剧下降，很快落地，保证筒口后方的人员不受伤害。

在整个发射过程中由于火药燃气被密封在筒内，所以实现了“三微”发射的要求。同时火箭弹和平衡体的质量和在筒内的行程相同，发射时的后坐力可以忽略不计。

2 建立内弹道模型

2.1 内弹道时期划分

根据平衡抛射火箭武器的工作原理，将其内弹道过程划分为两个时期。

1)定容燃烧时期。该时期从击发底火开始到发射药管断裂结束。燃烧室为前/后活塞之间的空腔区域，由于发射药管未断开，燃烧室容积不变，发射药定容燃烧。

2)变容燃烧时期。该时期从发射药管断裂开始到前后活塞停止运动结束。燃烧室随着活塞的前后移动逐渐变大，发射药持续燃烧到燃烧完全。活塞停止运动后火箭弹和平衡体与发射筒脱离。

2.2 假设条件

该火箭武器的发射过程和枪炮既有相同点也有不同之处。相同点：都是采用击针击发底火，靠点火能量点燃发射药，其采用的发射药类似榴弹发射器的圆片薄火药；都经历了定容燃烧阶段和变容燃烧阶段。不同点：相比普通炮弹，它没有弹带，即没有弹带嵌入膛线的过程和位移；装填密度远比枪炮类武器低；前后活塞到达筒口时瞬间停止运动，火箭弹和平衡体的惯性使其与前/后活塞连接处在瞬间撕裂而断开。

合理的假设使发射过程成为一个理想化的模型，简化计算的同时使计算结果接近试验数值。因此，对平衡抛射火箭武器的内弹道过程做出如下假设：

1)火药燃烧遵循几何燃烧规律。

2)药粒均在平均压力下燃烧，且遵循燃烧速度定律。

3)用系数φ来修正其他一些次要功。

4)筒内压力达到p0时，发射药管瞬间断裂，忽略固定杆对前后活塞的约束力。

5)火药燃气服从诺贝尔-阿贝尔状态方程。

6)采用增大热比κ或减小火药力f来对内膛表面热量散失进行间接修正。

7)单位质量火药燃烧所放出的能量及生成的燃气温度都是定值，在以后膨胀做功过程中，燃气组分变化不予计及，因此虽然燃气温度因膨胀而下降，但火药力f、余容α以及比热比κ等均视为常数。

8)整个内弹道过程中，前后活塞与筒壁之间不产生漏气现象。

9)火箭弹和平衡体与前后活塞连接处断裂时对火箭弹和平衡体的出筒口速度的影响忽略不计。

2.3 药形系数的计算

该火箭武器的发射药采用圆片薄火药，直径为2r，厚度为2e1，已燃厚度为e，药粒起始体积为

V1=2πr2e1.

(1)

药粒燃去体积为

V=V1-2π(r-e)2(e1-e).

(2)

令a=e1/r，Z=e/e1，根据火药几何燃烧定律[5]代入整理得：

ψ=χZ(1+λZ+μZ2),

(3)

2.4 定容、变容燃烧时期气态方程

2.4.1 定容燃烧时期气态方程

定容燃烧时期，燃烧容积不变，火药气体没有做功，且时间极短，忽略掉热散失后，此时的火药气体状态方程可表示为

(4)

式中：在筒内燃气压力达到启动压力p0时的ψ值为ψ0，在这一时期0≤ψ≤ψ0<1；ρp为火药密度；α为火药气体余容；f为火药力；Δ为火药装填密度。

在筒内达到启动压力时，pψ=p0，开始变容燃烧阶段。

2.4.2 变容燃烧时期气态方程

火箭弹和平衡体开始运动后，燃烧容积不断增加，设火箭弹和平衡体移动的距离为l1和l2，建立此时的变容状态方程如下：

(5)

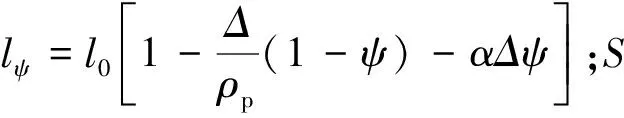
2.5 建立内弹道方程组

根据上述假设，可将内弹道方程组[5]归纳如下：

1)形状函数

ψ=χZ(1+λZ+μZ2).

(6)

2)燃速方程

(7)

式中：u1为火药燃速系数；e1为1/2火药起始厚度，即弧厚；Ik为火药气体压力全冲量；n为燃速指数。

3)运动方程

用平均压力p和次要功系数φ表示的运动方程

(8)

式中：m1、v1分别为火箭弹的质量、速度；m2、v2分别为平衡体的质量、速度；p为火药气体平均压力；t为运动时间。

4)弹丸速度与行程关系式

(9)

2.6 模型求解

该计算采用四阶龙格-库塔法对式(1)～(9)进行数值求解，运用MATLAB编写计算程序，得到内弹道的相关曲线，如图2所示。

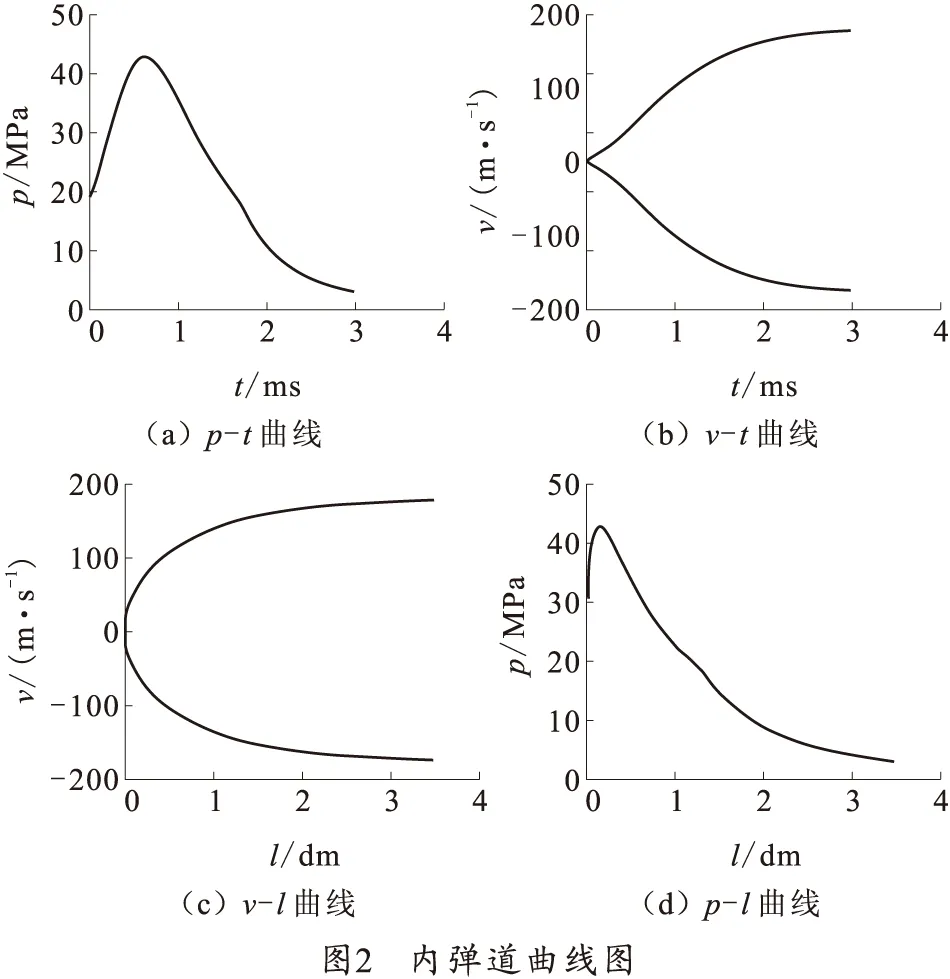
从图2中可以看出，在0.636 ms时，膛压达到最大值42.628 MPa，此后膛压逐渐下降，在3 ms火箭弹离开筒口，出筒口速度为175.22 m/s，膛内此时压力为2.683 MPa。由于火箭弹与平衡体的质量和行程相同，故在数值模拟中，其速度大小相等、方向相反。

3 火箭弹初速与最大膛压测试

弹丸在飞出筒口时，其后部连接的变形环被强制制动，弹丸与前活塞连接处在断裂瞬间对弹丸速度会产生一定的影响，因此火箭弹初速测试时要测出弹丸与前活塞连接处断裂前后的速度v1、v2，即筒内测速和筒外测速。本试验采用线圈测速法[6]，在弹丸尾部装一个永磁环，发射筒口布置一组感应线圈，筒口前部也布置一组线圈,如图3所示。弹丸通过线圈时会产生感应信号，记录下每组线圈的时间差。

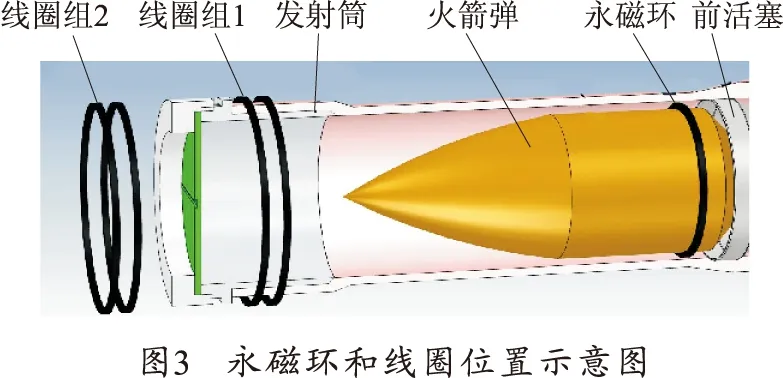
弹丸速度的计算表达式为

(10)

式中：L1，L2分别为线圈组1、2的距离；t1，t2分别为弹丸穿过线圈组1、2的时间。

在试验中随机抽取5具火箭筒，测得最大膛压值(铜柱测压法[7])及误差，如表1所示；测得火箭弹筒口速度v1、v2及误差，如表2所示。

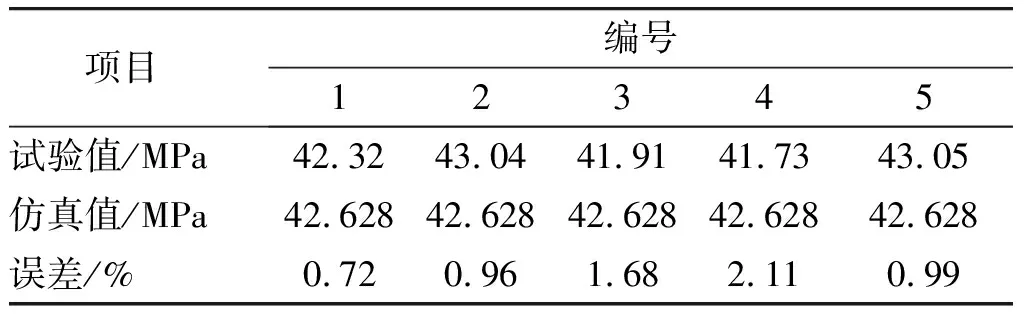
表1 最大膛压及误差表

注：误差=|试验值-仿真值|÷仿真值×100%.

表2 火箭弹筒口速度及误差表

注：误差=|速度v1-仿真值|÷仿真值×100%.

从表2中可以看出，速度v1比速度v2的值均稍微大一些，说明弹丸与前活塞连接处在断裂的瞬间造成了一定的能量损失，但从数值上来说速度值变化的非常小，验证了基本假设9；弹丸初速(即v1)与仿真值的误差在3%之内，表明仿真和试验的吻合性较好，证明了仿真模型的正确性。

4 结束语

笔者详细介绍了采用平衡抛射原理的火箭武器工作过程，对比了与普通枪炮武器的异同点，提出合理的假设条件，根据经典内弹道理论建立了仿真模型并使用MATLAB软件进行数值计算。通过试验数据验证所建立的内弹道模型和基本假设条件的正确性，为平衡抛射原理的推广应用提供了理论指导。