江淮地区老黏土的液限和塑限相关性分析
葛明洋, 吕锦伟
(安徽省水利水电勘测设计院,安徽 蚌埠 233000)
老黏土是江淮丘陵(岗地)区域最常见的土类之一,其液限是指黏性土从塑性状态到液性状态的界限含水率,塑限是从半固态到塑性状态的界限含水率,两者均能反映黏性土物理特性,是计算塑性指数、液性指数的直接指标,其大小受土粒组成、矿物成分、表面电荷强度及比表面积等因素影响。土工试验规范中测定塑限的方法有搓滚法和液塑限联合测定法,测定液限的方法有蝶式液限仪和液塑限联合测定法[2]。国内诸多研究表明,在一定范围内塑限和液限之间具有相关性,但地域特征显著[3]。本文针对江淮地区老黏土,以引江济淮工程江淮沟通段土工试验为例,尝试建立液限和塑限的线性相关模型,用以估算界限含水率和检验土工试验的准确性。
1 建立线性回归方程
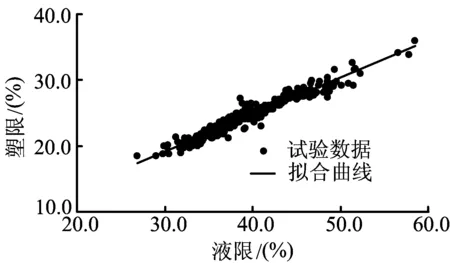
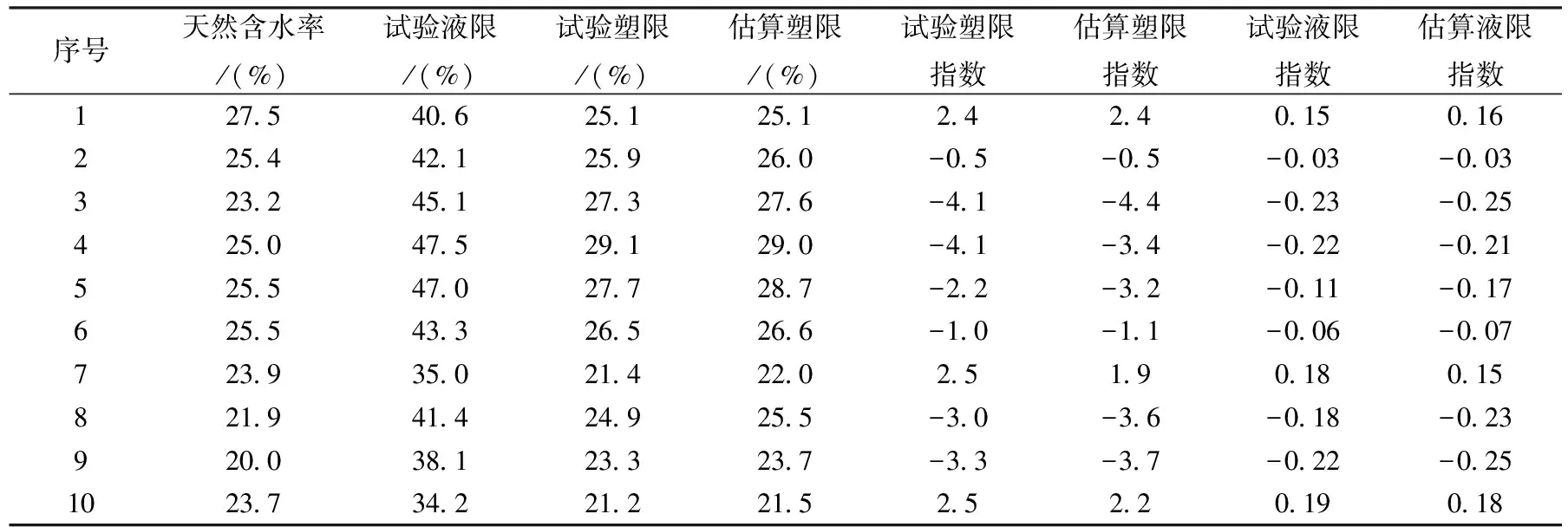
依据我院完成的引江济淮工程(安徽段)工程地质勘察报告[4],在江淮沟通段随机选取不同深度老黏土液限和塑限测试数据383组,由于篇幅限制仅给出数据12组如表1所列。界限含水率测试方法依据文[2],土类定名按水利工程定名,其中液限和塑限的取值范围分别为26.9 表1 引江济淮工程江淮沟通段老黏土液限和塑限部分试验数据 注:本表及下文数据及公式中涉及液限、塑限和天然含水率单位均为%。 若以液限值为X轴,塑限值为Y轴,试绘制了液限与塑限相关性拟合图1所示。图中反映除个别数据较离散,绝大多数实验数据具有相关性,即随着液限的增大,塑限呈线性增长,反之随着塑限的增大,液限亦呈线性增长,这里仅讨论已知塑限求液限的线性方程,塑限的求解过程同理可得。 图1 江淮地区老黏土液限和塑限相关性 令液限wL=x,塑限wp=y,依据一元线性回归方程:y=bx+a+ε,其中ε~N(0,σ2)为随机误差,是不可控制的。a和b为线性回归系数,具体公式[5]如下: (1) (2) 为验证上述回归方程是否合理,我们可以通过数理统计中F检验和t检验两种常用的方法检验其显著性,再比较实例加以验证。 表2 F检验计算值表 当置信水平α=0.01,样本数量为无穷大时,查F分布表可知,F0.01(1,∞)=6.64<5540.31,所以可以说明上述回归方程高度显著。 表3 t检验计算值表 计算结果t=74.64>2.58,假设被拒绝,b=0不成立,回归方程在置信水平α=0.01时具有显著性。 已知试验液限,利用所得回归方程求估算塑限、估算塑性指数及估算液性指数如表4所列。与试验数据进行对比分析,由于篇幅有限仅列举十组随机数据。 由表4可得,试验塑限与估算塑限的差值在-0.6~0.1范围内,试验塑性指数与估算塑性指数的差值在-0.7~0.6范围内,试验液性指数与估算液性指数的差值在-0.01~0.06范围内,并不影响老黏土的土类命名及塑性状态判别,差值均在可接受范围内,上述线性回归方程可以估算塑限值,或者为土工试验的准确性检验提供参考。 表4 老黏土物理性质指标计算结果比较 江淮地区老黏土液限和塑限呈线性增长关系,即随着液限的增大,塑限呈线性增长。液限和塑限的线性回归方程为wp=0.56wL+2.36,反之亦然,所得线性回归方程经检验具有显著性。利用所得线性回归方程可以在已知液限时估算塑限值,亦可为土工试验的准确性检验提供参考。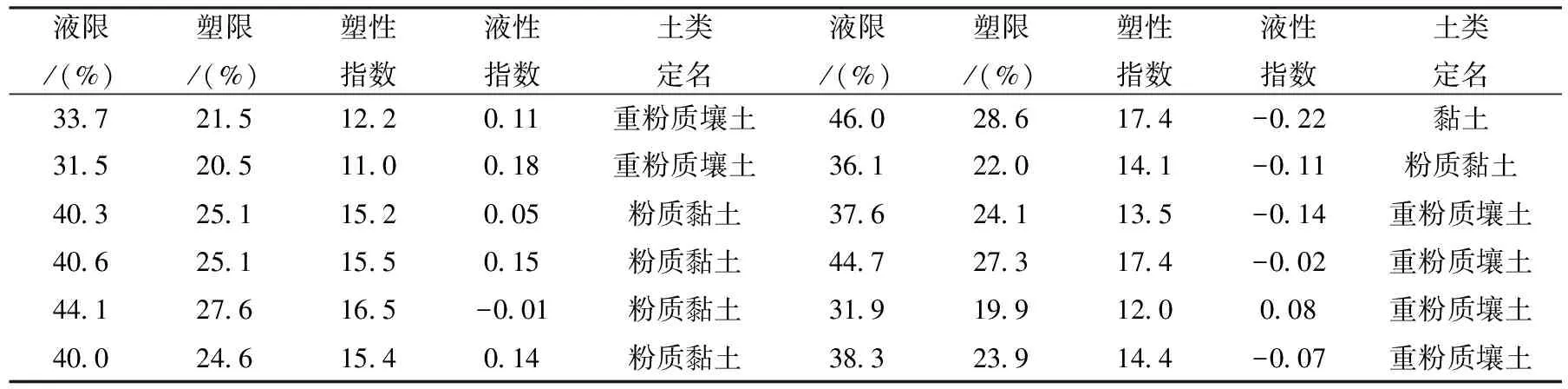
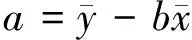
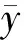
2 显著性检验
2.1 F检验
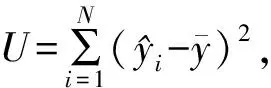

2.2 t检验
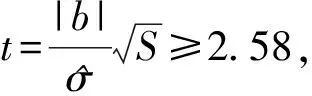

2.3 实例比较
3 结 论

