基于大数据分析的台风灾害经济风险评估

伍俊杰，黄 浩，潘 晨

(1.广东海洋大学数学与计算机学院，广东 湛江 524088；2.广东海洋大学海洋与气象学院，广东 湛江 524088)

台风灾害是广东省最主要的自然灾害之一，其引发的风暴潮及洪涝和山体滑波等灾害对社会基础设施和生命财产造成巨大的损害。

台风灾害评估是防灾减灾的关键，但由于台风的复杂性，其经济损失预测一直是一个难题。我国学者在致灾因子和灾情结合评估研究采用数理统计方法[1- 2]和模糊数学方法[3]。台风是一个涉及大量资料运算的自然界现象，因此，引入大数据分析技术有助于掌握台风的动态。本文尝试以大数据分析数据挖掘方法，利用多维度多角度的数据寻找关联性，从看似琐碎不相关的数据集合中挖掘对模型优化有用的因子，并使用机器学习中具有自我反馈学习的预测模型对最终结果进行预测。最后，基于这个预测模型再运用气象灾害风险管理的方法做出台风经济风险的统计和预测。

本文对台风的经济风险解读基于灾害学领域的观点，即自然灾害事件(包括量级、时间、场地等要素)发生的可能性以及由其造成后果的严重程度。对台风灾害有可能带来的经济损失以及此损失的可能性做出估计。

1 背景及相关技术介绍

1.1 背景

1945—2015年期间，共计216个台风直接登录广东省，其中低压强登陆有27个，热带风暴级别和以上级别的共计189个，省内各沿海城市登陆数据如图1所示。

图1 登陆广东省沿海城市台风数量(1945—2015)

由图1可知，广东省湛江市是历年台风登陆数目最多的城市，也是受台风灾害冲击最为惨烈的城市，而且其他数据表明到目前为止登陆广东省的最强台风Rammasun(17+级，62m/s，910hPa)也正是登陆自湛江市徐闻县龙塘镇，可见湛江市在防灾减灾形势十分严峻。

1.2 相关技术

1.2.1 BP神经网络的原理

BP(Back Propagation)神经网络模型是一种按误差逆传播算法训练的多层前馈网络[4]，通过最速下降法，反向传播来不断调整网络的权值和阈值使得网络的总误差最小[5]。模型拓扑结构有输入层、隐藏层和输出层组成。第j个神经元的净输入值Sj见式(1)。

(1)

式中，wji—神经元i与第j个神经元的权值；xi—分别输入层神经元的输入；bj为阈值。

模型运算结构如图2所示。图2中，f(x)—传递函数；yi—第j个神经元的输出。

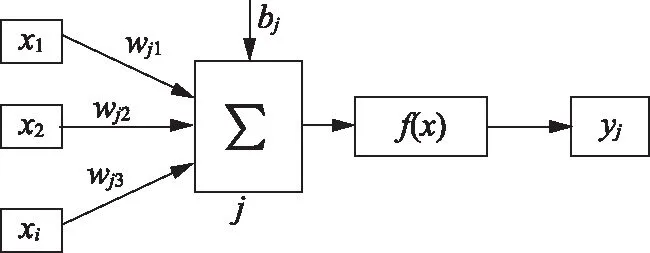
图2 BP神经元

当正向传播完成后需要反向传播，即通过累计误差去调整网络中的权值wji，使总误差减少。关于BP神经网络更详细的算法可参考文献[6]。

1.2.2 LS-SVM的原理

LS-SVM是建立在在SVM基础上的改进，LS-SVM从机器学习损失函数上做出改进，在优化问题中优化目标的损失函数为误差的平方，同时LS-SVM约束条件将SVM中采用的不等式变为等式[7]。并且LS-SVM引用了核函数，最后只需通过对线性方程组的求解实现二次规划问题的化简，通过降低求解难度的方式，大大提高运算速度并且能够保证最后结果有较高的精度[8]，更详细的算法过程可参考文献[9]，最后可得到非线性方程(2)：

(2)

式中，K(x,xi)—核函数，K(xi，xj)=φ(xi)·φ(xj)。

2 大数据分析技术与预测

2.1 大数据转换过程

大数据的数据转换过程可分为各类型不同数据的前提收集、中期对各类型数据的压缩和分析及最后结果的输出，如图3所示。

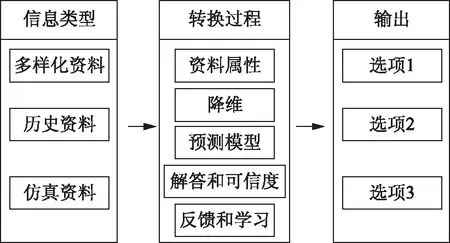
图3 大数据的转换过程

由于大数据对一些图像、音像等多样化数据的量化提取技术尚未成熟和广泛运用，本文对图3中的信息类型仅局限于数字文本资料，转换过程基本一致，但最后输出本文的数据只有直接经济损失这一个选项。

2.2 数据降维

大数据在数据维度上具有广泛性，尽管前期对数据选取已经作了筛选，但大量基于时间序列的数据在各维度上仍然可能存在较严重的线性相关性。大数据中，最常用的数据降维方式是通过压缩数据的线性关系已达到高维度数据最终向低维度映射的目的，减少计算资源的耗费与提高运算速度[10]。由于大数据的数据多元，因此，维度可以无限大，本文只选取了部分相关的数据维度作出筛选分析，见表1。

表1 广东省台风数据因子选取

数据在以上维度的数值，经标准化处理后利用机器学习中的降维方法，主成分分析法对多维度数据进行降维，主成分分析的降维方法在对数据特征压缩原理上是基于一个协方差矩阵进行的，因此可以大大减少因子间的线性相关性。大数据的维度在量纲上存在差异，在降维前应进行标准化处理和中心化处理，数据降维后可发现前6个主成分的贡献率在90%以上，因此选取这6个主成分作为后期预测模型的因子输入，降维结果的时间序列分布如图4所示。

图4 降维结果时间序列分布

2.3 直接经济预测

台风灾害造成的直接经济损失受大数据多维度的数据影响，但由于某些影响因素具有很强的随机性，因此预测难度非常大，如果沿用一般的多元线性回归方法有可能会导致精度非常低。本文在对台风于广东省的直接经济损失预测将结合大数据中的反馈学习和模型自我调节优化的特点和要求，将运用机器学习中的两种算法，BP神经网络和LS-SVM(最小二乘支持向量机)对数据进行预测，并从精度和效率上评价这两种算法在大数据预测中的效果。针对数据中每10次台风数据给出两个预测值，即以前10次台风数据作为训练集以预测下两次的经济损失。原始数据是已经进行降维后得到的6个主成分。

2.3.1 利用BP神经网络预测

由降维后的6个主成分作为BP神经网络的输入层，每次台风的直接经济损失数据作为BP神经网络的输出层，通过样本数据对网络进行训练，最后得到直接经济损失的预测值，Matlab中就有相应的神经网络工具箱可以进行对数据的训练和仿真。本文采取预测点的前10组样本数据作为训练集来对往后2次台风的直接经济损失进行预测，以此类推，通过训练样本的每两组地向后移动，形成适用于后两次数据点预测的神经网络，即最新权值，完成后样本数据集两次台风直接经济损失预测。由于数据库准备前期已经对数据进行了归一化处理，不需要再对数据进行归一化处理去除量纲。利用广东省1985—2015年台风登陆的数据样本，每10组作为训练集，预测往后2次的经济损失，样本窗口每两次向后推移，预测点也将同时向后推移，直到得到往后所有点的预测结果。将预测所得结果与相应台风序号的实际数据做比较，如图5所示。

图5 利用BP神经网络法预测结果

2.3.2 利用LS-SVM预测

利用LS-SVM进行预测时，将由降维后的6个主成分作为影响因子的输入，每次台风的直接经济损失数据作为输出。运用Matlab中的LS-SVM工具箱对样本数据进行训练和最后结果预测。

本文将选定高斯径向基函数作为LS-SVM的核函数，因为它的应用范围最为广泛并直接反映了两个数据的距离。另外在选定核函数之后，LS-SVM模型还需对超参数γ(对应惩罚因子C，决定训练误差)和核参数σ^2(决定样本的分布和范围，与方差成反比)，以上两个参数的选取须在合理的范围内选取，γ太高容易造成过度拟合[11]，在工具中有一个函数Gridsearch可以在一定的范围内进行参数寻优，以找到较为适合的参数值。同理，对数据中每10组作为训练集，得到最新的训练网络，以此预测往后2次的经济损失，然后按照预测点的推移，训练样本随之转移，最后完成全部经济损失值的预测结果并与实际值进行对比，结果如图6所示。

图6 利用LS-SVM法预测结果

2.3.3 两种预测方法结果对比分析

(1)运算速度：从算法原理出发，由于人工神经网络因本身传递函数具有非线性映射以及算法收敛比较慢的特征，而LS-SVM则在算法中直接采用核函数代替高维特征空间中的内积计算问题并通过对线性方程组的求解实现二次规划问题的化简，这样能够显著提高模型的训练速度，在对台风灾害直接经济损失的预测实验中，实际情况明显低说明两种算法在运算速度上的优劣，因为本实验中BP神经网络在前后推移中一共用了大约15s，而LS-SVM则只用了1s左右，并且两个算法在编程上的结构也是类似的，都用到了for循环来进行训练集的推移。

(2)精度分析：在精度对比时，本文将引入绝对百分比误差(Absolute Percentage Error)概念，即表2中的APE，对两种算法的预测精度进行量化，最后结果见表2。

(3)

式中，Y—实际值；Y′—预测值。

表2 结果对比 单位：亿元

由表2可得，BP神经网络绝对误差小于50%的数目为19个，而LS-SVM算法预测得到的结果中绝对误差低于50%的数目为25个，要高于BP神经网络法预测得到的结果。因此，在精度上也可以认为LS-SVM广东省台风灾害的直接经济损失预测上在大多数点的准确率要高于BP神经网络，尽管一些点上LS-SVM法的预测值误差会高于BP神经网络法的预测值误差，并且有个别点也会出现误差爆炸的情况，当出现误差爆炸时，可以认为模型预测已经没有意义，但到底是什么原因导致模型预测出现误差爆炸的情况是今后需要发展和模型改进的方向之一。

因此，在台风灾害直接经济损失预测中，从预测值准确率上LS-SVM的预测精度会稍高于BP神经网络法，但从运算速度上，LS-SVM模型通过核函数在非线性函数与线性函数的巧妙转化，使得LS-SVM法在运算速度上要大大高语BP神经网络法，LS-SVM更适合语解决大规模数据计算问题，在台风大数据分析中，数据规模非常庞大。经比较，相比BP神经网络法，选用LS-SVM法进行数据预测会更有效率，并且更节省计算机运算占用的内存，减少不必要资源浪费。

3 结语

本文对台风灾害的经济风险的大数据分析过程作了介绍，包括前期的数据抓取、转换和清洗、多维度数据的压缩降维和利用预测模型对数据进行预测，分析和反馈学习，不断提高数据预测的计算精度。并且就台风经济损失数据，利用机器学习中的两种用于回归预测的常用算法作出模拟作为一次实验，最后从运算速度和精度上对两种模型于台风大数据中的应用作出分析与评价。

基于台风灾害直接经济损失的预测对BP网络和LS-SVM比较分析得出在大数据预测过程中LS-SVM更为适合。但预测结果仅仅局限于某个预测值，而不是预测值的置信区间，这是今后研究和改进的方向之一，在实际应用中往往后者会具有更大的参考价值。