山间河谷盆地潜水层地下水位动态变化预测

任焕莲

(长治市水文水资源勘测分局，山西 长治 030001)

潜水含水层地下水位动态深受气候、水文、地理地质条件限制，不仅与降水多少、降雨强度，气温、日照、蒸发有关，且与埋藏条件等诸多因素有关，这些因素之间又有着错综复杂的关系，因此，运用结构性的因果分析模型往往较困难。应用时序分析法的季节周期-ARMA组合模型，根据潜水层水位观测资料，提取和分析历史资料本身所蕴含的信息，找出其规律并利用这些规律，达到预报未来的目的，给地下水动态预报分析带来极大便利，且该方法易于掌握和应用推广[1]。

近30多年来，时序分析理论已广泛用于地下水资源评价、预报和管理，并有大量的著述。常用的时序模型有灰色时序组合模型、RBF神经网络、小波随机耦合模型、灰色马尔柯夫链模型、时间序列分析模型等[2- 10]。随着计算机技术的广泛应用，发展了多种模型，例AR、MA、ARMA、ARIMA、乘积型季节性模型、门限模型等，这些模型应用灵活方便且具有较高的模拟精度。

本文应用季节周期组合分析法对长治市山间河谷盆地地下水水位动态进行分析，揭示了该区地下水动态变化规律，提供了较为准确的地下水位动态模拟和预报数据，为长治盆地地下水合理开采和科学管理提供依据。

1 季节周期组合模型原理

潜水层水位动态变化的不确定因素较多，水位变化既有周期性也有随机性，本文用一定的周期和随机模型分析其变化过程。平稳时间序列基本形式是xt=μt+yt，通常称μt为序列的确定性部分，yt称为零均值的平稳随机部分。ARIMA模型是采取一些办法剔除μt部分的作用，季节周期-组合模型不仅要将趋势性和周期性分量分离出来，而且要给出μt的具体表达式，因此建立起既有确定性又有随机性部分的组合模型，由这两部分组合来共同描述某些类型的非平稳过程，可以达到令人满意的结果[11]。

1.1 建立组合模型的方法[11]

选用最小二乘法按照某类函数拟合数据序列的确定性部分，从低阶开始，逐渐增加阶数，直到模型无明显改进为止。然后对消除了确定趋势的残量序列建立适宜的ARMA(n，m)模型。最后，用前述得到的两部分参数估值作为初值，对确定部分和ARMA部分的所有参数，用非线性最小二乘法重新估计，得出组合模型的最终估计。

针对某些时间序列，不仅含指数趋势，而且还呈现出某种规律的周期性起伏，则可用如下形式的组合模型去拟合。

(1)

式中，{yt}—ARMA(n，m)序列；L—序列所含有的指数趋势项的项数；K—周期趋势项的项数；φ—基频，弧度/s，(由数据的物理性质决定)；Bj和rj—表示周期趋势的振幅和相位；ebjt—控制周期振荡的增长或衰减趋势。

地下水埋深时间序列数据不仅受降水强度、大小影响，而且与气温，地理条件及岩性、水位埋深厚度有关。周期趋势不一定是对称的。为此将式(1)改为如下形式。

(2)

式中，‖·‖—时间t除以周期长度s的小数部分，0≤‖t/s‖≤1，d为指数。显然当d=1时，式(2)和式(1)是等价的；当d<1时，式(2)表达的周期趋势为上升较下降快；但当d>1时，式(2)表达的周期趋势为上升较下降慢。

1.2 组合模型建模的具体步骤

首先拟合线性或指数趋势，然后逐个增添周期趋势项，最后对残差序列{yt}建立ARMA模型。各个分模型参数估计出来后，再以它们作为初值，对整个组合模型统一进行参数估计。尽管模型待估计参数个数较多，借用DPS7.05数据处理系统来实现序列分析与拟合，估计过程借助计算机反复使用非线性最小二乘法。

建立模型的过程即是从已知序列(观测值)(xt)(t=1、2、3…、n)中提取各分量的过程，提取的顺序为：趋势分量、周期分量和随机分量。一旦建立了各分量的数学模型后，再将其线性叠加，就得到了式(2)形式的地下水位埋深预测模型。

2 季节周期-ARMA组合模型对地下水位埋深的实证分析

长治盆地潜水层地下水相对丰富，开发利用程度比较高，对长治市的国民经济建设起着重要作用。本次研究选取长治盆地多个具有代表性地下水潜水层长期观测井进行分析预报，限于篇幅，本文仅以长治盆地东部南关地下水观测井为例，用该观测井1994—2011年月平均地下水位动态资料，建立地下水动态时间序列季节周期组合模型并对模型进行分析。

2.1 模型参数识别

首先提取趋势项分量和周期项分量，剩余进行自回归模型识别，得到各分量参数，模型阶数的确定，本文采用了AIC准则[12- 13]。将趋势分量、周期分量和随机分量叠加，得到地下水水位埋深预测模型，即组合方程：y=x0t+x1t+x2t+…+xnt+X(t)。各分量参数见表1，各分量计算公式如下：

时间序列趋势方程：x0t=6.76849×EXP(-0.01233t)

表1 各分量参数及T检验值

序列的第1个周期方程：

x1t=-2.68196×EXP(-0.02176t)×sin{2×3.14159×‖t/36.0‖^(0.43277)+3.907423}

序列的第2个周期方程：

x2t=902.78898×EXP(-0.07717t)×sin{2×3.14159×‖t/96.0‖^(7.04084)+6.3098}

序列的第3个周期方程：

x3t=0.78718×EXP(0.00124t)×sin{2×3.14159×‖t/156.0‖^(2.27318)+5.711756}

序列的第4个周期方程：

x4t=0.22397×EXP(-0.01189t)×sin{2×3.14159×‖t/12.0‖^(1.29295)+4.778517}

序列的第5个周期方程

x5t=-27.91849×EXP(-0.13802t)×sin{2×3.14159×‖t/9.0‖^(20.12089)+1.273318}

序列的自回归滑动平均模型为ARMA(3，3)：

X(t)=1.1699-0.044958X(t-1)+0.010247X(t-2)+0.018617X(t-3)-1.251609E(t-1)-0.831299E(t-2)-0.288085E(t-3)+e(t)

模型的残差平方和ss=7.0252，残差标准差=0.1938，AIC=-41.0890，相关系数R=0.99778，拟合度c=99.56%。

2.2 对所建模型进行精度检验

潜水层地下水位动态变化时序组合模型建立后，模型精度是否满足，需要对建立的模型进行检验。对潜水层观测井的地下水动态变化时间序列模型的预测值与实测值进行对比，拟合结果如图1所示。

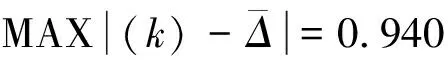
图1 计算值和实测值拟合曲线

(2)事后检验，即对已建立的模拟模型用于预报前进行精度检验，本文用未参加建模的2012年水位埋深资料进行后验预报检验。t取n+1～n+12时(n取216)，可得到各月水位埋深预测值。其后验预测结果见表2和图2。

模型拟合平均误差εavg=5.36%，预测精度达94.64%。从图2和表2看出该模型预测精度也较高，其最大绝对误差0.16m，最小达到了0.03m，相对误差均小于9%，满足精度要求，该模型可应用于预报未来地下水水位。从图2中知，预测时在峰值处拟合稍差，这是因峰值往往对应着随机因素的突变，由此产生模型预报误差。

图2 后验预测拟合曲线

图3 2013—2024年预报水位埋深曲线

2.3 预测预报

模型在进行实际预报前需进行反复调参，直到满足精度要求。现依据经过精度检验了上述预报模型，预报长观井2013—2024年各月地下水位埋深。水位预报值和曲线分别见表3和图3。

表2 后验预测误差

表3 2013—2024年逐月预报水位埋深值 单位：m

3 结论及建议

(1)建立的潜水层水位动态季节周期-ARMA组合模型，拟合精度和预测精度均较高，模型反映出了盆地潜水层水位变化的趋势性、周期性和随机性，提示该区域水位动态变化规律，是一种较好的模拟预测模型，可以为该区域地下水资源合理开发和规划提供可靠依据。

(2)对模型周期项分析，该区水位动态有5个主要周期成分，即存在13年、8年、3年周期成分，间接反映了多年气候变化，另有2个小周期1年及9个月，反映了一年内降水的季节性周期变化。

(3)用实测资料建模是用系统过去的规律对未来进行预测，当某些因素在未来时刻有较大变化时，模型预报误差将增大，为此模型不足之处，是今后时序预测分析方法改进方向，使季节周期-ARMA组合模型的应用前景更加广阔[15]。