水库移民城市楼房安置的社会适应性评价分析

张 丹，王 丹，李贵博，姚凯文

(华北电力大学可再生能源学院，北京 102206)

1 研究背景

随着我国农村城镇化发展以及人多地少的矛盾，政府机构在充分尊重移民的意愿上进行了新的探索和试验，各种新型移民安置方式应运而生，在非农安置模式下的农村水库移民将会面临更多生产、生活和心理上的困难。

城市楼房安置模式是指由政府统一在城镇修建楼房，成立社区，移民自愿按照成本价购买社区住房进行安置，云南青山嘴水库在进行移民安置时首次采用了该种安置模式。随着移民搬迁进新建的栗子园社区，其生活方式、生产模式和居住环境与搬迁之前完全不同，各种关于搬迁、安置和恢复的问题和矛盾也随之产生，因此有必要对青山嘴水库移民的社会适应性进行评价和分析。

从对水库移民社会适应性的整体研究状况看，学者们的研究范围集中在以农业为主的传统安置方式，对于新型农村水库移民安置方式的社会适应性评价较少，且现有研究成果多数是调研后进行思辨讨论和定性描述，理论验证过程和评价系统不强。本文研究方向是在目前研究现状的基础上，针对城市楼房安置的水库移民以及加强理论评价系统继续研究其社会适应性。

2 青山嘴水库城市楼房安置评价指标体系构建

2.1 社会适应性内容

对于城市楼房安置的水库移民来说，搬迁后的生产生活等多方面发生了巨大变化，需要逐渐适应，主要体现在以下几个方面，见表1。

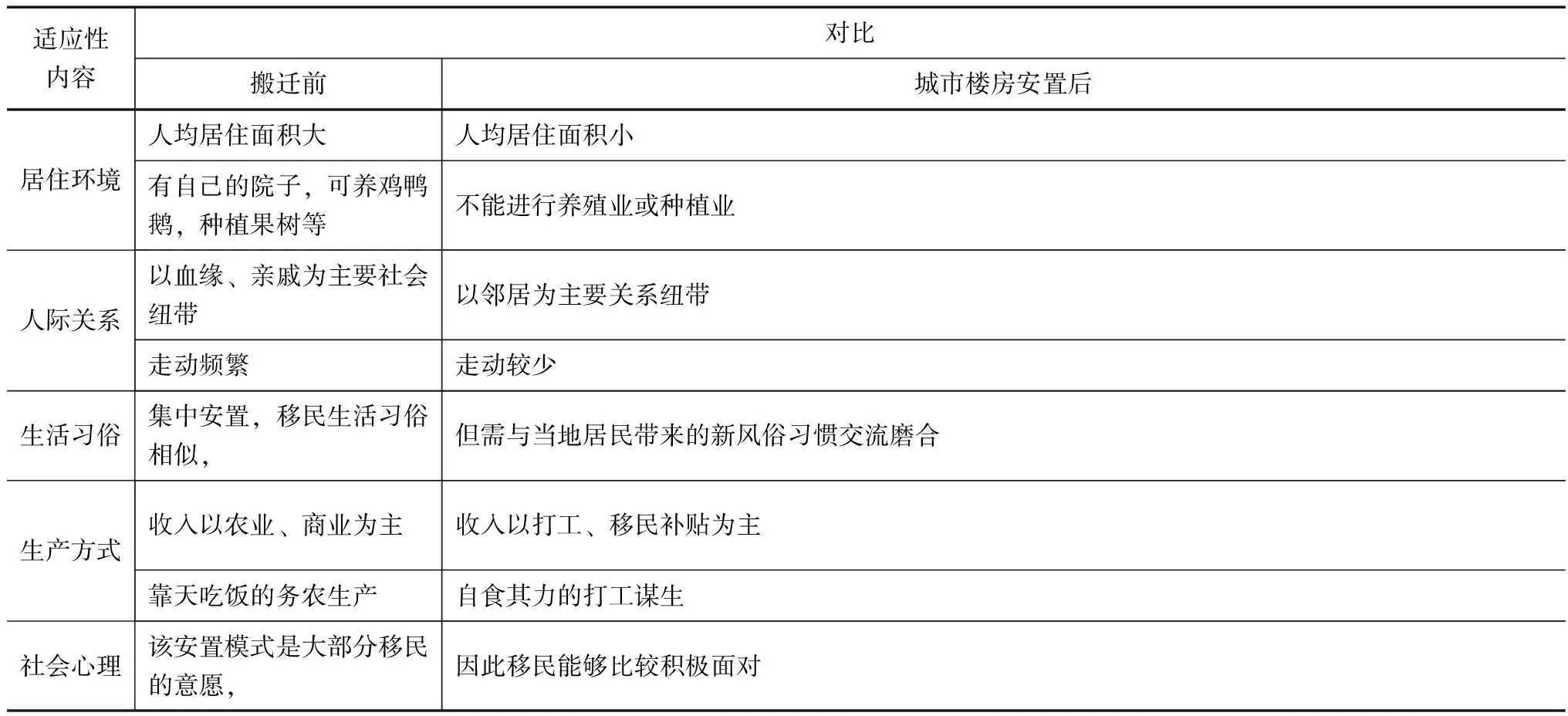
表1 水库移民城市楼房安置搬迁前后的变化对比表

2.2 评价指标体系的建立

根据前文有关社会适应性的内容阐述，选取其中差异最大的经济适应性、生活适应性以及人际关系适应性3个维度进行纵向分析。在单个维度的条件下，需要进行数据的调查与计算分析，如图1所示。

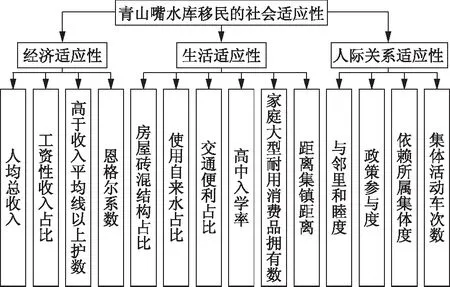
图1 水库移民城市楼房安置的社会适应性评价指标体系

3 水库移民城市楼房安置社会适应性评价的模糊物元模型

3.1 模糊物元分析方法

3.1.1 模糊物元与复合模糊物元

物元是指用“事物、特征、量值”来分析和计算以达到描述事物的基本元。如果其中的量值具有模糊性，使用有序三元组“事物、特征、模糊量值”作为描述事物的基本元，则该物元就称为模糊物元，记为：

(1)

若以R表示为模糊物元，则物元矩阵可以表示为R=(M，C，μ(x))，记为：

(2)

式中，M—事件；C—事物所具有的特征；μ(x)—与事物特征C相应量值x的隶属度，即模糊量值。

对于具体的事物，其模糊量值为具体的数值，本文研究的模糊量值为具体的数值，直接用量值Xji表示，这种复合物元，称为m个事物n维的复合物元，则有：

(3)

式中，Rmn—m事物n维复合物元；Xji—第j个事物的第i个特征相应的量值Xji。

3.1.2 从优隶属度矩阵

优隶属度指各单项指标相应的模糊值从属于标准方案各对应评价指标相应的模糊量值隶属程度。各评价指标特征值对于方案评价来说，有的是越大越优，有的是越小越优，因此，对于不同的隶属度分别采用不同的计算公式。

计算隶属度的公式有很多，为了更充分地反映社会适应性评价各指标的相对性，采用如下形式：

越大越优型：

(4)

越小越优型：

(5)

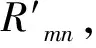
(6)

3.1.3 建立标准模糊物元和差平方模糊物元

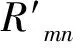
若以Δij=(μ0j-μij)2(i=1， 2， …,n;j=1， 2， …,m)

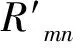
(7)

3.1.4 欧氏贴合度和综合评价

贴近度是指被评价样品与标准样品两者互相接近的程度，其值越大表示两者越接近，反之则相离较远，从而就可以根据贴近度的大小来对各事物的优劣进行排序，也可以根据标准值的贴近度进行类别划分。

考虑到本课题移民社会适应性的具体评价意义，采用欧氏贴近度ρHj作为评价标准，采用M(·，+)模式，即采用先乘后加的运算模式来计算和构建贴近度复合模糊物元RρH：

(8)

(9)

式中，wi—第i个特征指标的权重值，Δij—第j个事物的第i个特征的差平方复合模糊物元。

3.2 熵权法确定指标权重法

目前在实际评价应用中，常用的定权方法很多，有专家评分法、层次分析法(AHP)等主观赋权法，但是这些方法确定的权重会受主观性影响较大。本文为避免主观因素造成评价结果的偏差，引入熵值法确定权重系数。在信息系统中的信息熵是信息无序度的度量，信息熵越大，信息的无序度越高，反之亦然，故可用信息熵来评价所获系统信息的有序度及其效用。

本文由熵权评价指标值构成的判断矩阵来确定指标权重，能够尽量消除各指标权重计算的人为主观的干扰，使评价结果更加符合实际。计算步骤如下：

(1)构建m个事物n个评价指标的判断矩阵R：

Rmn=(xij)(m×n)(i=1，2，…n;j=1，2，…m)

(10)

(2)将判断矩阵归一化处理，利用以下公式得到归一化判断矩阵B：

(11)

式中，xmax、xmin—同一指标下不同事物中最满意者或者最不满意者，(越小越满意或越大越满意)。

(3)根据熵的定义，m个评价事物n个评价指标，可以确定评价指标的熵为：

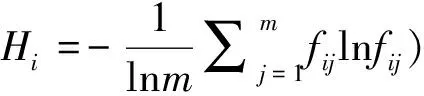
(12)

(13)

(4)计算评价指标的熵权W：

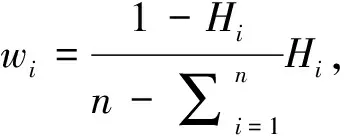
W=(wi)1×n

(14)

4 计算结果与分析

4.1 数据来源

笔者连续跟踪青山嘴水库移民样本户从2006—2015年经历的搬迁安置前可行性研究、搬迁安置动员、搬迁安置开始、搬迁安置进行中以及后期扶持的各个阶段，对各项指标进行抽样入户调查，再结合青山嘴水库移民的实际情况，确定以2006—2015年度选取典型年调查的数据进行横向分析。因此，本文采用的数据具有可靠性和可操作性，各项评价指标值见表1。

4.2 评价结果

根据上述方法，将原始数据归一化处理得到判断矩阵B；根据式(12)、(13)计算判断矩阵B的熵H；将该熵H分为整体与单维度两个方面，利用式(14)分别计算评价指标的熵权；最后，根据式(9)和式(10)计算欧氏贴近度复合模糊物元矩阵得到：

表1 青山嘴水库移民的社会适应性指标量统计表

根据计算结果，可作出青山嘴水库移民社会适应性历年欧氏贴近度折线图如2所示。

图2 青山嘴水库移民社会适应性历年欧氏贴近度折线图

4.3 分析与建议

4.3.1 评价分析

通过建模计算结果说明以及图2的趋势图看出，城市楼房安置下水库移民适应当地社会是一个必要和缓慢的过程，是重建有效的社区和新的社会结构必不可少的过程，青山嘴水库移民在2009年搬迁结束后的社会适应性欧氏贴近度才达到61%，通过几年的发展，移民在青山嘴水库栗子园社区安置点的适应程度逐年增加，已经在慢慢适应当地的生产生活。

通过单维度建模计算可以看出，移民的经济适应性、生活适应性、人际关系适应性的欧式贴近度都逐年增加，但总体趋势不同。①水库移民的经济适应性总体呈线性相关，适应性逐年增加，表示移民的经济水平逐年提高，移民收入逐年提高。②水库移民的生活适应性从2007年开始到2009年急剧增加，说明当时移民的生活发生巨大的改变，需要迅速调整生活方式来适应新的社区生活。2010年之后生活适应性增加速度变缓，可以看出移民还在进行调整和适应城市生活。③水库移民的人际关系适应性从一开始较高，当时移民还未搬迁，人际交往网络还未破坏，到搬迁时达到最低，但随着移民安置后不断适应当地的环境，人际关系适应度逐渐增加。

4.3.2 建议

通过本文的研究和评价，为让移民在安置点能够尽快适应当地的生产生活，提出以下几点建议：

(1)对移民正确的思想引导

农村水库移民一般生活水平较低，思想单纯而传统，故土难离的观念根深蒂固。由于未来生活的不确定，农村水库移民的思维心态从相对稳定变为相对不稳定。因此，要对移民的思想进行正确引导，让他们有“安全感”。政府部门需要积极引导移民，鼓励移民利用各种途径勤劳致富，同时加大宣传力度，使水库移民能够明确看到未来的生活将优于现在，那么水库移民的心态随着搬迁后生产生活的稳定而能够较快的重新稳定。

(2)保障移民的公众参与和协商权益

移民安置的主体是移民群众，移民的参与是移民安置过程中的重要内容。政府和设计单位在制定移民安置政策、计划编制和实施阶段，已经十分重视移民的参与和协商，保障移民的参与权。在移民搬迁进入社区后更要保障移民的公众参与和协商权益，充分调动移民的主观能动性，让他们在城市社区有主人翁的心态去积极发展自身经济，主动融入当地城市生活，转变自己的思想和习惯。

(3)让移民能够稳定就业

政府已经通过一系列的措施让移民能够就业，保障了移民的基本生活来源，但是移民多数就业的工作类型为临时工，工作的稳定性不能得到保障，所以当地政府应该结合地域经济发展，因地制宜，量身定做，在移民中积极扶持发展产业项目，让移民相比于搬迁之前有更多的致富渠道和资源，逐渐摆脱贫困，对未来的生活充满斗志和美好的愿景。

(4)鼓励和促进移民与城市居民良性交往

城市楼房安置的最终目的就是让移民能够在城市居住下来，与城市居民能够共同致富，完全融入当地社会的一切事务中。政府应该鼓励和促进移民与城市居民进行良性交往，在经济、政治、文化等方面进行融合。要对移民和城市

居民一视同仁。在移民搬迁过程中，不应享有特权，而是平等权。同时多制造一些社区联谊文化活动，让移民与当地城市居民和睦相处、健康发展。

5 结论

根据实地调查，目前青山嘴水库移民安置区的房屋建设和基础设施建设已完成，移民已经搬入新居，移民对目前的生活总体满意，正逐渐适应当地的生产生活，经济水平也在不断提高。通过将模糊物元模型运用在水库移民的社会适应性评价上，从定量的角度更加有效地反映了城市楼房安置水库移民的社会适应性现状，同时也帮助政府在对新型移民安置方式的探索和尝试上提供了新的思路。从评价结果看，本方法的评价结果较为客观，城市楼房安置下水库移民适应当地社会是一个必要和缓慢的过程，是重建有效的社区和新的社会结构必不可少的过程。