齿轮转动惯量对电动汽车传动系统振动特性的影响分析
刘海妹,陈云飞
(1.常州工学院航空与机械工程学院/飞行学院,江苏 常州 213032; 2.中达电子(江苏)有限公司,江苏 苏州 215200)
分布式驱动电动汽车将驱动电动机直接安装在驱动轮内或驱动轮附近,车轮由单个驱动电机驱动[1]。由于结构发生了变化,分布式电动汽车的扭转振动响应有别于传动内燃机汽车和集中式驱动电动汽车,因此,减速器的齿间问题对传动系统扭转振动的影响一直是研究热点。
目前国内关于减速器对传动系统扭转振动的影响在多方面开展了研究并运用了多种方法。文献[2]综述了近20年来齿轮振动噪声的研究现状和发展趋势。文献[3]建立了齿轮副三维空间弯曲-扭转-轴向耦合的非线性动力学模型,分析了齿面摩擦对齿轮副周期振动的影响规律。文献[4]通过Solidworks建立了行星齿轮减速器的实体模型,选取减速器的传动系统机构及集成箱体机构,进行了有限元模态分析。文献[5]以Hyper Works软件为平台,建立了某汽车减速器上箱体的有限元模型,并使用RADIOSS求解器进行了模态分析和频率响应分析。
本文拟建立分布式驱动电动汽车传动系统的集中质量模型,计算不同减速器齿轮转动惯量的分布式驱动电动汽车传动系统的振动特性,分析比较不同的减速器转动惯量对传动系统固有特性的影响,总结减速器转动惯量对传动系统固有特性的影响规律。
1 建立传动系统数学模型
某分布式驱动电动汽车传动系统示意图如图1所示,轮边单机驱动,经减速器增扭减速,通过驱动半轴将驱动力传动给车轮。
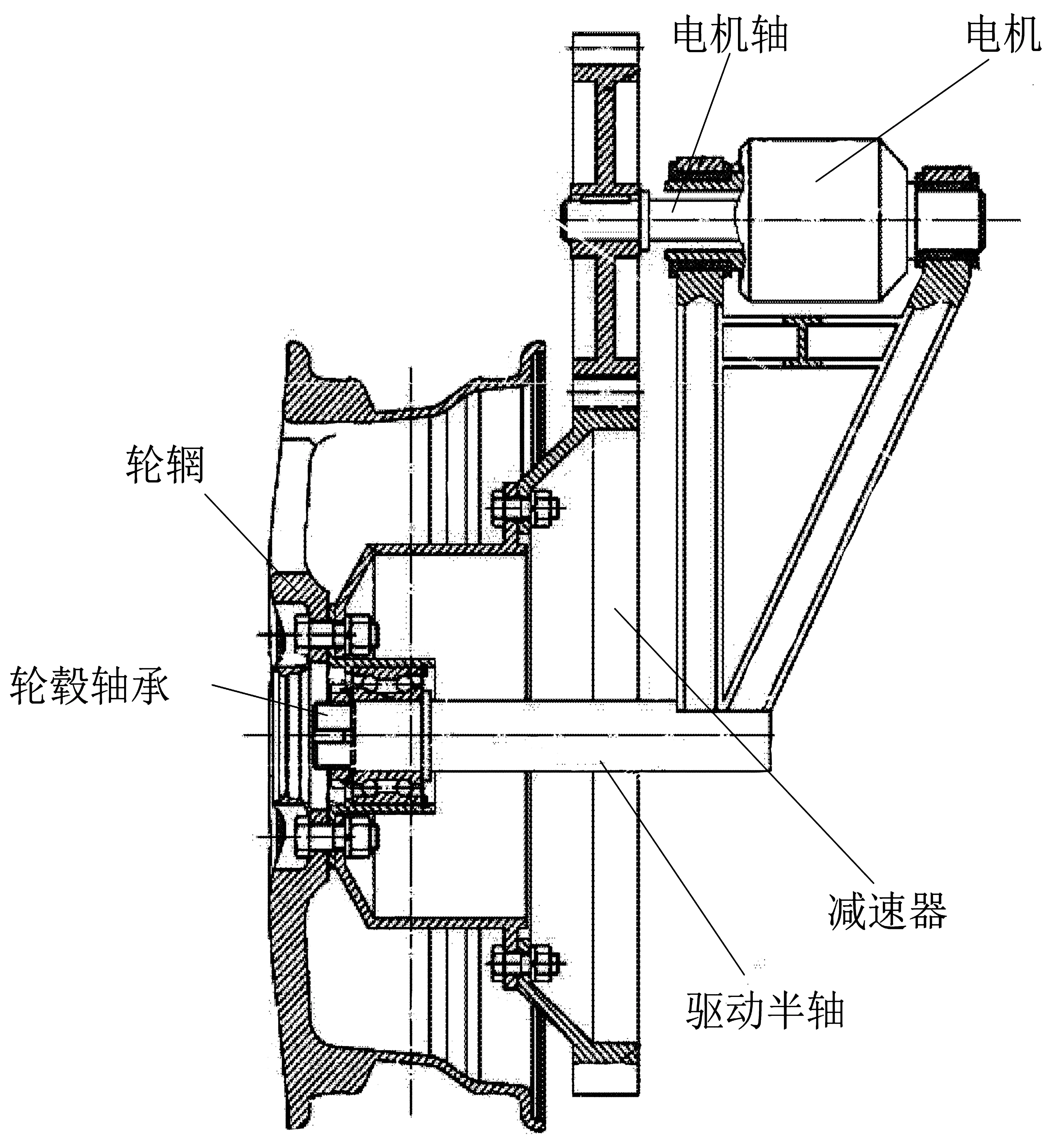
图1 轮边电机驱动-传动系统示意图
采用集中质量法将分布式驱动电动汽车传动系统简化为有限自由度的模型,简化规则如下:1)齿轮均简化为只有转动惯量的当量圆盘;2)忽略系统的阻尼[6];3)忽略轮胎、齿轮副非线性特性。
1.1 减速器模型的简化
忽略齿轮系统的非线性特性,按照能量守恒的原则,将减速器的输入端与输出端转动惯量等效为惯量盘[7]。对于减速器的齿轮啮合方面,由于齿轮间的连接刚度和啮合刚度都很大(数量级在107),因此,将齿轮啮合近似看成刚性啮合,只对转动惯量进行等效。图2为某电动汽车减速器齿轮等效简图。

图2 减速器转动惯量等效简图
建模时遵循动势能守恒的原则,将输出轴上的齿轮转动惯量等效至输入轴上,等效原则公式[8]:
(1)
式中:JA、JB为主动轮和从动轮转动惯量;θa1、θa2为主动轮转动角度和从动轮转动角度。
1.2 电机的简化
电机转子的转动惯量较大,抗扭转能力强,将其简化为惯量盘。电机轴为一个阶梯轴,扭转变形较大而转动惯量较小,考虑为弹性轴。
1.3 半轴的简化
半轴为细长轴,由于细长轴的刚性较差,抗扭转变形能力弱,转动惯量小,考虑为无质量的弹性轴。
1.4 轮胎和车身的简化
忽略轮胎非线性特性,将车轮简化为一个惯量盘,并通过等效弹簧与整车平移质量等效惯量相连接[9]。
1.5 传动系统自由振动数学模型
多自由度系统的固有特性主要是指固有频率和主振型,固有特性通过求解无阻尼振动方程得到,无阻尼振动方程为[10]
J{θ′′}+K{θ}=0。
(2)
根据上述简化规则,建立分布式驱动电动汽车传动系统集中质量模型,如图3所示。

图3 传动系统集中质量模型
根据自由振动系统运动微分方程(2),得出分布式电动汽车传动系统数学模型:
(3)
式中:Ji表示各当量圆盘转动惯量;Ki表示各轴段扭转刚度;K2/i表示从输出轴扭转刚度等效到输入轴后的扭转刚度;θ2/i表示从输出轴扭转角度等效到输入轴后的扭转角度。
2 计算传动系统振动特性
物体做自由振动时,其运动特性随时间按正弦或余弦规律变化,振动的频率与初始条件无关,仅与系统的固有特性有关。固有特性由式(3)计算得出,无阻尼自由振动方程的解为
{θ}={φ}sin(ωt+θ)。
(4)
将式(4)带入式(3)中,解得
([K]-ω2[M]){φ}={0}。
(5)
若{φ}有非零解,则上式中{φ}的系数行列式解为零,即:
det([K]-ω2[M])=0。
(6)
由于无阻尼振动方程为齐次方程,主振型{φ}结果不唯一,需要对结果进行归一化处理[11-12]。
系统振动方程的通解为
{θ}{φa}sin(ω1t+a)+{φb}sin(ω2t+a)+{φc}sin(ω3t+a)+{φd}sin(ω4t+a)。
(7)
2.1 刚度、转动惯量的数据选取
本文选取的传动系统转动惯量与刚度如表1所示。

表1 传动系统转动惯量与刚度
根据已有模型和台架试验参数,选取了3组减速机参数[13-15],假设3组齿轮副分别为S1、S2、S3,选取尺寸如表2所示。

表2 减速器转动惯量 kg·m2
根据式(1)计算得出等效转动惯量JD1、JD2、JD3。
2.2 固有特性的计算
将各部分转动惯量及刚度带入式(3)并结合系统振动方程通解,得到3组固有频率ω及主振型如表3、表4、表5所示。

表3 S1传动系统固有频率及主振型
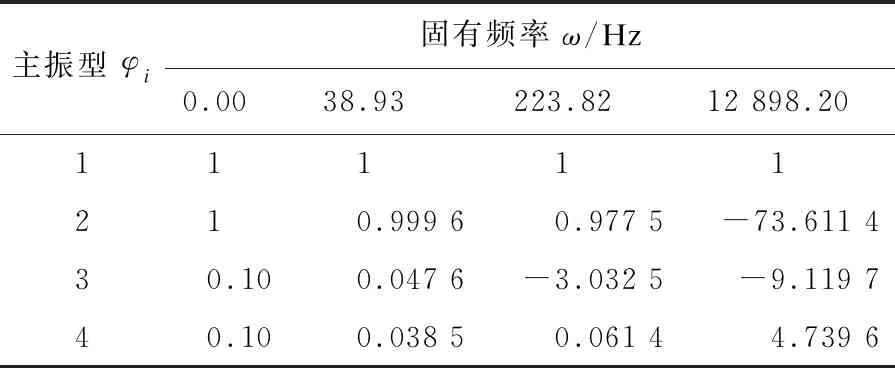
表4 S2传动系统固有频率及主振型
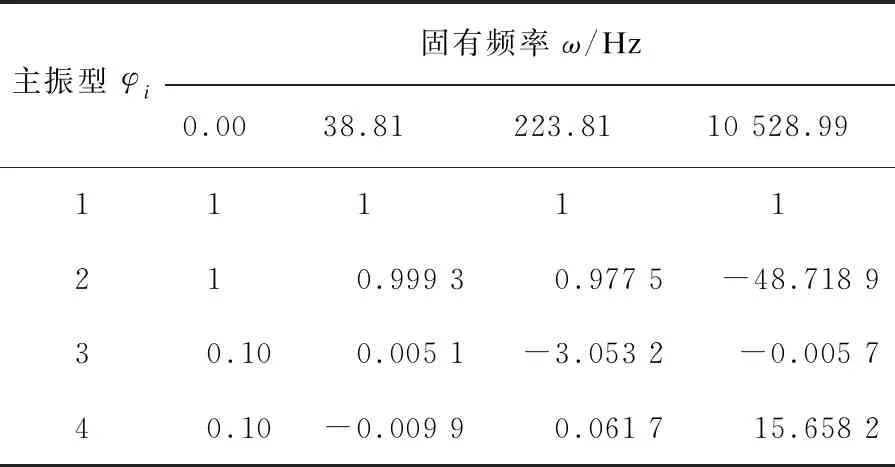
表5 S3传动系统固有频率及主振型
表中ω为固有频率,i对应第i个自由度。由表可以看出由于尺寸变化整车平移质量的固有频率会有10%~20%变化,并且变化规律不随减速器等效转动惯量的增大而增大。
3 传动系统扭转角响应
将固有频率ω及主振型{φ}带入式(7),利用Matlab进行分析计算,并绘制转角时域图,分析比较不同减速器转动惯量对转角响应变化趋势的影响。
图4、图5、图6和图7为0~10 s传动系统各部分转角响应曲线。分析图片可知,由于减速器尺寸不同,传动系统各部分转角幅值和非线性特性有所变化。
图8、图9、图10和图11为0~0.01 s传动系统各部分转角响应曲线。分析该组图得出,传动系统振动频率发生变化,记录并分析幅值频率变化如表6、7所示。
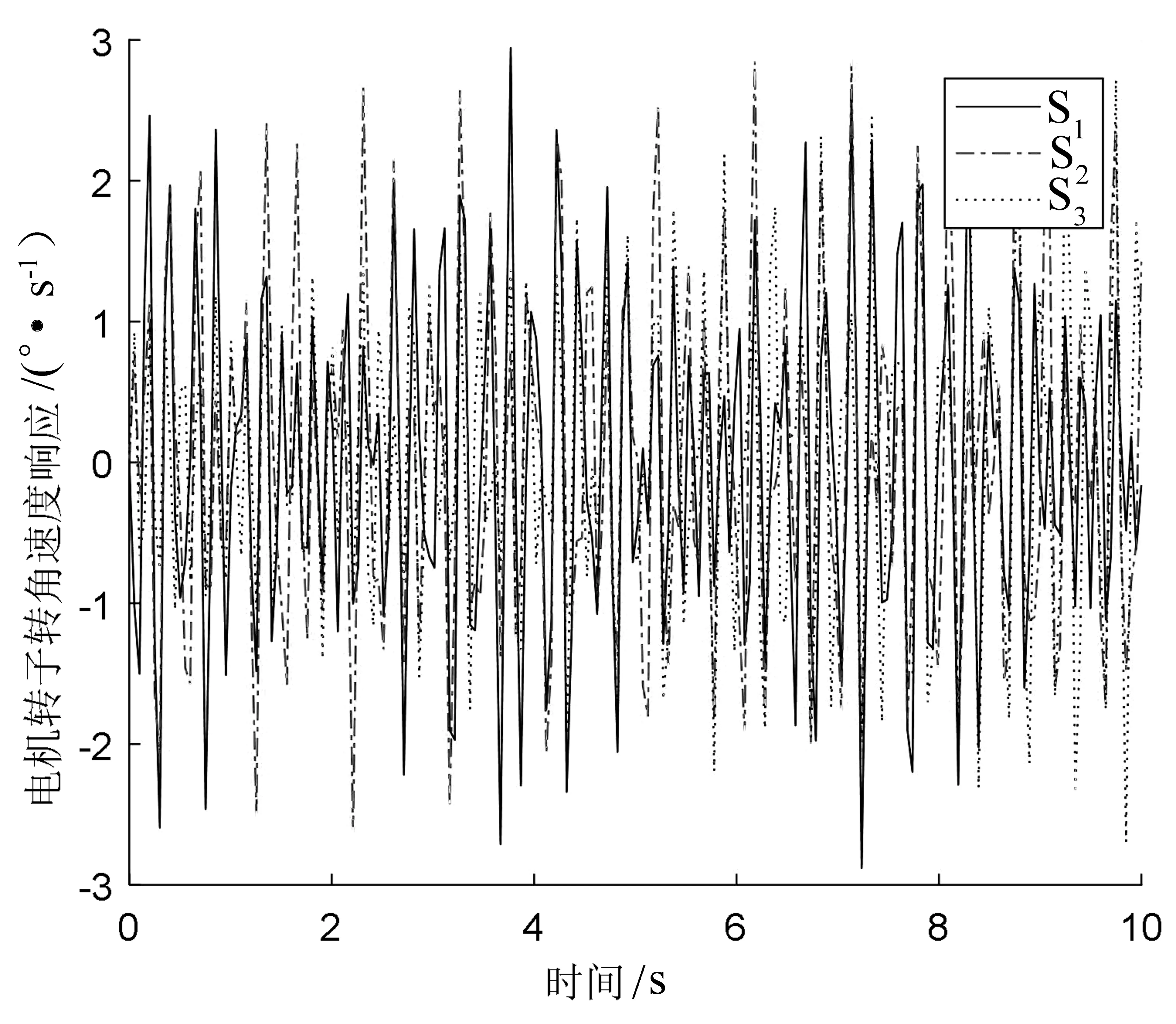
图4 电机转角时域响应(0~10 s)

图5 减速器转角时域响应(0~10 s)

图6 车轮转角时域响应(0~10 s)

图7 整车平移质量转角时域响应(0~10 s)

图8 电机转角时域响应

图9 减速器转角时域响应

图10 车轮转角时域响应

图11 整车平移质量转角时域响应
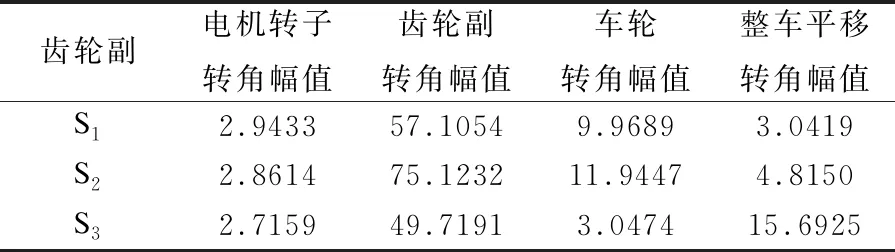
表6 幅值比较 (°)

表7 频率比较 Hz
4 结论
对电动车传动系统中不同减速器尺寸的模型求解得到的固有特性进行了分析和比较,结果表明:
1) 传动系统减速器尺寸的不同,会影响系统振动特性且为非线性特性。
2) 由于减速器尺寸不同,传动系统中各部分转动幅度受到影响,对扭转刚度、强度提出了不同要求。除此以外,传动系统中大部分角频率有微小变动,只有整车平移转角转动角频率变动较大。
3) 减速器传动比过大或过小,都会增加系统中某部分的振动。因此,在选取减速器时,需根据需要选择合适的传动比。
4) 在今后的研究中,对不同固有频率对系统扭转振动影响进行探讨。

