基于局部哈希学习的大面阵CCD航拍图像匹配方法

陈苏婷，郭子烨，张艳艳

(南京信息工程大学 江苏省气象探测与信息处理重点实验室,江苏 南京 210044)

引言

大面阵CCD数字成像技术以其几何性能好、对平台稳定度要求较低、应用处理便捷等优点[1]，已逐渐成为获取对地观测信息数据来源的主要途径，随着航拍影像成像技术和计算机技术的高速发展，超高分辨率CCD航拍相机相继问世。随着大面阵CCD图像的数据量剧增，如何实现快速有效的特征点匹配是近年来CCD图像处理技术的研究热点。为实现航拍影像的特征点匹配，首先需采用特征检测算法提取特征点并构建特征描述子；在此基础上，根据相似性度量实现匹配。其中，特征描述子构建是实现快速匹配的关键[1-5]。针对特征描述子构建，文献[6]提出将SIFT(scale-invariant feature transform)[7]与KDES-G(gradient kernel descriptor)特征[8]进行级联融合获取联合向量，以提高特征描述子的鲁棒性。SURF(speed up robust features)算法[9]针对SIFT算子实时性不高、并且对于边缘光滑目标的特征点提取能力较弱等问题，通过使用Hessian矩阵检测特征值可精确定位特征点。上述基于浮点型的特征描述子匹配准确率较高，但过高的计算复杂度不适合海量高分辨率航拍影像的实时匹配。为此，二值型特征描述子如BRIEF(binary robust independent elementary features)算子[10]则可大大降低特征描述向量的维度。ORB(oriented FAST and rotated BRIEF)算法[11]则将FAST(features from accelenated segment test)特征点的检测方法[12]与BRIEF特征描述子结合，进一步提高匹配速度，但也导致了匹配准确率大大降低。

相对手工设计的特征描述子，近期在机器学习的研究热潮推动下，基于学习方法构建的特征描述子正成为值得期待的探索研究方向，其中，哈希学习作为机器学习领域的研究热点，得到国内外研究学者的高度关注[13-15]。然而，哈希学习目前主要用于整幅图像的信息检索，无法直接应用于海量高分辨率航拍图像的特征匹配。

针对上述图像匹配中存在的计算复杂度和匹配速度间的矛盾，本文提出了局部多特征哈希(LMFH)匹配算法，通过局部匹配区域构建、局部哈希学习方法、目标函数构建及参数优化等关键问题研究，实现了航拍影像特征点的高效匹配，为航拍影像快速匹配实现提供新思路，对超高分辨率航拍影像数据处理及应用领域具有重要意义。

1 CCD航拍图像匹配方法

本文提出的LMFH匹配算法分为3部分：局部多特征描述子构建、哈希学习算法和哈希匹配算法，算法流程如图1所示。首先对获取的CCD航拍图像进行特征点检测，构建局部多特征描述子；针对该特征描述子，提出了LMFH算法构建局部哈希学习函数；将该函数获得的二进制哈希代码映射到汉明距离，实现快速哈希匹配。

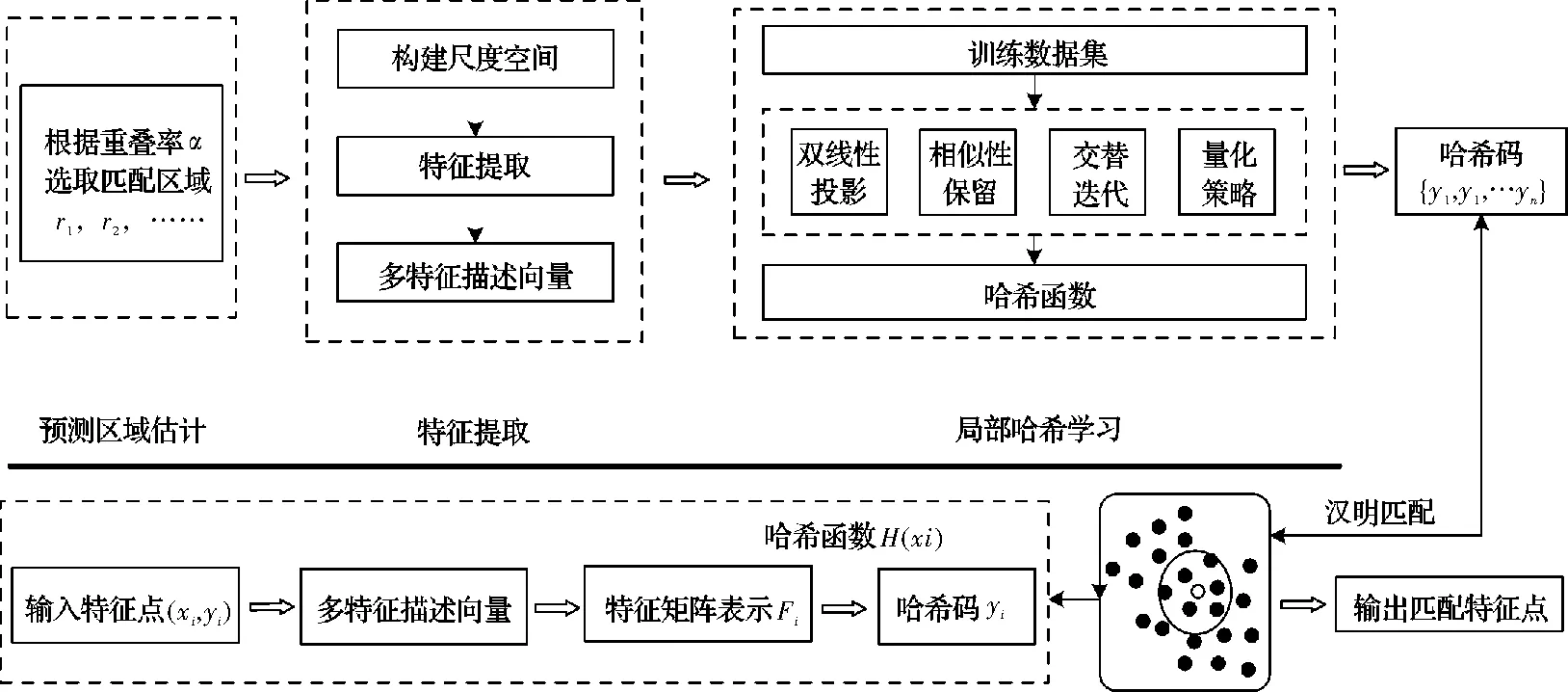
图1 大面阵CCD图像特征点匹配方案Fig.1 Feature points matching scheme of large array CDD aerial images

2 基于局部多特征的CCD航拍图像哈希匹配

2.1 局部多特征描述子

一般来说，待匹配的两幅航拍图像之间重叠度较高，为减少计算复杂度，提出了基于预测区域的特征描述子构建方法。

首先，根据航拍图像重叠率估计预测区域；然后，通过构建尺度空间金字塔，在每个尺度图像上，采用FAST算法[12]进行兴趣点检测，使得检测到的角点具有尺度不变性；对提取到的特征点，以特征点为中心选取邻域，确定特征点的主方向，并将中心邻域旋转至主方向上，以实现特征的旋转不变性；在邻域内，提取多种特征信息，包括：梯度特征、平均强度特征、方向特征和局部纹理特征，组合多种特征，得到高维特征点描述向量fi∈RD。

2.2 局部多特征哈希学习

LMFH算法的主要任务是学习特征描述子的二元表示。首先，特征向量fi表示成矩阵形式Fi；然后采用双线性投影矩阵Θ1、Θ2定义哈希方程H(Fi)；为保留特征点的相似性关系，定义相似性标签，并根据标签信息构建目标优化函数，实现哈希函数参数的获取；最后，使用交替迭代算法学习映射矩阵{Θ1、Θ2}，实现框图如图2所示。针对图2，本文提出的局部哈希学习算法的具体实现流程如表1所示。

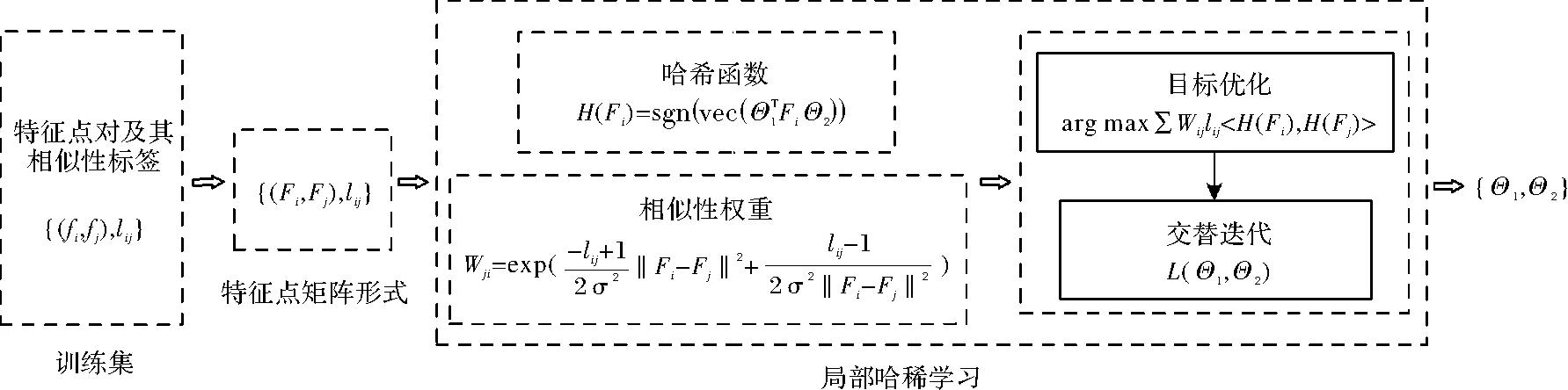
图2 多特征哈希学习方法Fig.2 Multiple features hash learning method

算法:LMFH哈希函数学习算法输入:训练特征点集{F1,F2,…,FN}。输出:双线性投影矩阵Θ1、Θ21) 预处理:中心化数据集fi←1NNj=1fj),i=1,…,N;2) 将所有的特征向量fi转换为矩阵形式Fi,i=1,…,N;3) 构建局部特征点对的集合P,获取特征点对间的标签信息lij;4) 计算相似性权重Wij;5) 初始化投影矩阵Θ1、Θ2;6) 选代以下过程;7) Θ1←M1(Θ1);8) Θ2←M2(Θ2);9) 目标函数L(Θ1,Θ2)收敛;10) 返回投影矩阵Θ1、Θ2。

2.3 快速哈希匹配

通过哈希函数构建，高维特征向量会被映射到紧凑的二进制哈希编码。匹配之前，通过构建汉明查找表来建立哈希编码和特征点信息间的索引。匹配阶段，在待匹配图像上根据汉明距离寻找对应匹配点，实现图像快速匹配，如图3所示。

图3 基于汉明查找表的航拍图像特征匹配Fig.3 Aerial image feature matching based on Hamming lookup table

3 实验结果与分析

从实拍的UAV航拍图像[16]中选取3组航拍图像做对比实验，实验结果如图4所示。用提出的LMFH算法和经典的ORB[7]、BRIEF[6]和SURF[5]算法作重复率、匹配准确率、匹配时间方面的比较。

图4 分组的航拍图像匹配结果比较Fig.4 Comparison of matching results of aerial images in group

3.1 重复率比较

重复率表示每组图像之间对应的特征点数量与经过特征点检测算法后得到的较少特征点数量之比，定义如下：

(1)

不同算法的3组航拍图像重复率对比结果如表2所示。

表2 重复率比较Table 2 Comparison of repetition rate

从表2中可知，LMFH算法在特征检测部分重复率最高，在3组航拍图像中，平均重复率为83.9%；BRIEF算子的平均重复率为49.7%，相比LMFH算法减小约34.2%；ORB算子的平均重复率为57.7%，相比LMFH算法减小约26.2%；SURF算子的平均重复率为82.4%，相比LMFH算法减小约1.5%。综上所述，将LMFH算法用于实际航拍图像特征提取时，检测到的特征点重复率最高，性能稳定。

3.2 匹配正确率比较

正确率表示每组图像中正确匹配的特征点数量与两幅图像间对应的总的匹配点数量之比，定义如下：

(2)

3组图像的具体实验数据如表3所示。

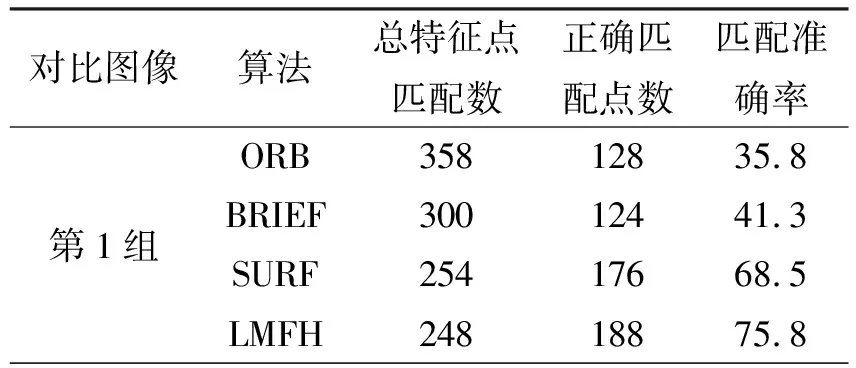
表3 匹配正确率比较分析Table 3 Comparison analysis of matching accuracy

续表

从表3中可以看出，在第1组匹配实验中，LMFH算法正确率为75.8%，相比于ORB算子高40%，相比于BRIEF算子高34%，相比于SURF算子高10%；在第2组匹配实验中，LMFH算法的正确率为71.5%，相比于ORB、BRIEF和SURF算子分别高33%、31%和10%；在第3组匹配实验中，LMFH算法的匹配正确率为65.6%，相比于ORB、BRIEF和SURF算子分别高23%、24%和12%。从3组匹配实验结果可知，在实际CCD航拍图像特征匹配中，本文提出算法的匹配正确率最高，BRIEF算子的匹配正确率最低。

3.3 匹配速度比较

匹配速度表示从开始对图像进行处理到匹配出正确的特征点对时所用的时间。匹配速度越快，算法的运行效率也就越高。通过比较匹配时间，比较各算法的匹配效率。3组航拍图像的匹配时间对比如图5所示。

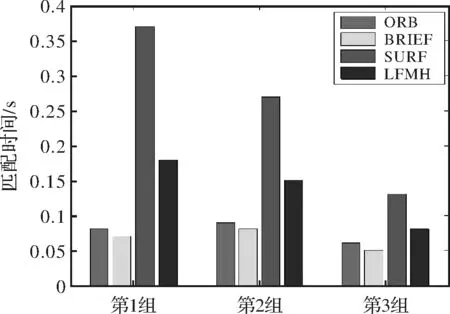
图5 匹配速度比较结果Fig.5 Comparison result of matching speed

从图5可知，在匹配速度方面，二值型特征描述算子的匹配时间最少，如ORB和BRIEF；相比之下，SURF算子的匹配时间最长，约为二值型特征描述算子的两倍，原因在于：在SURF算法中，特征描述子为高维浮点型特征向量，匹配时根据向量间的欧式距离进行比较，计算量大；LMFH算法的匹配时间介于两者之间，原因在于：LMFH算法在特征描述子构建和局部哈希学习部分耗费较多时间，但在匹配阶段，本文采用学习到的哈希函数，将高维的特征描述向量映射为二进制哈希编码形式，通过汉明距离即可实现特征间的快速匹配。除此之外，本文在匹配策略方面采用分段匹配方案，可进一步提高匹配速度。

4 结论

本文提出基于LMFH算法实现大面阵CCD航拍图像精准快速匹配，和许多传统的算法相似，LMFH算法使用各种各样的具有高精准度的统计特征来保证匹配准确度。然而，LMFH算法通过使用高效率的哈希目标函数并没有产生处理大量特征而带来的低效率问题。实验结果表明:LMFH算法的检测准确率相比于普通的手动设计的二值型特征描述算子如SURF算子、ORB和BRIEF算法，分别提高约10%、40%和34%，同时重复率最高，匹配速度最快。基于LMFH算法的匹配方案在确保特征匹配的准确率的同时实现特征的快速匹配。