面齿轮传动啮合刚度分析与修形减振优化
付学中, 方宗德, 贾 超, 彭先龙
(1. 西北工业大学 机电学院,西安 710072;2.西安科技大学 机械工程学院,西安 710054)
轮齿变形和啮合刚度的精确计算是研究轮齿齿面修形、振动与噪声、动态特性、寿命预测、故障诊断的基础[1-2],也是确定齿轮传动系统内部附加动载荷、齿面载荷分布及齿间载荷分配系数的重要因素。关于轮齿变形和啮合刚度的计算方法[3-4],国内外学者已进行了大量的研究,并形成了以材料力学方法和数学弹性力学方法(即保角映射法)为代表的理论计算方法、以边界元法和有限元法为代表的数值计算方法。
材料力学方法是使用最早应用最广的一种方法,以Ishikawa公式和Weber-Banaschek公式最具代表性[5],前者在日本和国内应用较多,后者在国外应用较多[6]。但材料力学方法因对精确渐开线齿形进行了简化(如Ishikawa公式中将轮齿简化为长方形与梯形的组合、Weber-Banaschek公式中将轮齿简化为变截面悬臂梁),并忽略了齿根过渡曲线的影响,致使计算精度和可靠度较低。数学弹性力学方法是基于弹性力学理论和复变函数保角映射理论,先将齿轮的曲线边界映射成直边边界,再求解轮齿的半边界体在集中力作用下的受载变形[7-8]。数学弹性力学方法计算精度依赖于映射函数的精度,但合理选取映射函数是非常困难的,且该方法只适用直齿轮平面问题,并不可直接应用于斜齿轮问题。另外,材料力学方法和数学弹性力学方法均假设啮合线上各点位移相同,且载荷沿接触椭圆长轴分布均匀,这与实际严重不符,也无法考虑安装与制造误差、齿面误差与修形的影响,更难以描述轮齿复杂的几何形状、实际受载状况及边界条件。数值计算方法则有效克服了上述不足[9-11],尤其是有限元法在工程中已得到广泛应用,采用有限元法分析锥齿轮传动、准双曲面齿轮传动的变形和啮合刚度,其计算结果精度较高[12]。
面齿轮传动是航空航天领域先进的新型传动,在直升机均载分流传动方面优势明显[13],但面齿轮齿面复杂[14],齿厚沿齿宽变化较大,故准确求得面齿轮传动啮合刚度的解析式极其困难。目前,国内外仅见少量关于面齿轮传动啮合刚度计算方法的公开文献,研究也有待进一步深入。李政民卿等将面齿轮齿形近似成由沿齿高或齿宽方向变化的一系列切薄片组成,采用材料力学方法推导了面齿轮啮合刚度计算公式,并分析得到了压力角、模数及齿宽等设计参数对面齿轮啮合刚度的影响[15-16],但因采用的是简化后的当量齿形,前述材料力学方法的固有缺陷并未改进。唐进元等[17]提出将面齿轮传动传动误差换算成沿啮合线方向的轮齿弹性变形量,并按轮齿刚度定义计算啮合刚度的方法,但是面齿轮传动承载传动误差采用商业有限元软件ABAQUS求解,存在计算时间长、前后处理操作繁琐、计算效率低等问题,且不利于将其嵌入到优化设计等相关程序中去。此外,以上研究均是针对面齿轮传动理论齿面,并未考虑变位、小轮偏置、安装误差和齿面修形等对啮合刚度的影响。
本文基于面齿轮传动承载接触分析(LTCA)技术,建立了面齿轮传动啮合刚度求解模型,分析了变位、小轮偏置和安装误差对面齿轮传动综合啮合刚度均值和波动幅值的影响,并将LTCA技术与遗传算法相结合,建立了以修形参数为优化变量,以综合啮合刚度波动幅值最小为目标的面齿轮传动修形减振优化模型,为进行面齿轮传动系统动力学分析和修形齿面设计提供理论参考。
1 面齿轮传动啮合刚度求解
本文采用Zhang等[18-19]提出的LTCA技术分析面齿轮传动,该方法采用三维有限元法、柔度矩阵及数学规划法求解轮齿的三维弹性接触,成功地结合了齿轮几何分析和力学分析,是获得加载条件下轮齿工作性能的重要分析工具,且其高精确性和有效性已被试验所证实[20-21]。本方法优点有:①含齿根过渡曲面在内的面齿轮全齿面齿廓由刀具展成获得,齿形未进行任何简化,同时还考虑了轮体的轮缘,并自动生成有限元网格,单元形状规整,故模型本身具有很高的精度;②有限元法计算轮齿工作齿面结点柔度系数时只需进行一次,而啮合周期内不同啮合位置的接触线离散点法向柔度矩阵只需重新插值即可,计算量小,耗时少,效率高。
进行面齿轮传动LTCA前,需要先做如下准备工作:①获得综合考虑变位[22]、小轮偏置[23]、齿面修形的面齿轮传动大、小轮全齿面轮齿有限元模型;②建立含轴向位移误差Δq、偏置误差ΔE、轴夹角误差Δγ的啮合坐标系,将大、小轮齿面坐标变换到啮合坐标系下进行齿面接触分析(TCA)求解,得到大、小轮齿面初始接触间距矢量w和几何传动误差TEG;③采用有限元方法计算轮齿工作齿面结点柔度系数,采用二元插值法确定齿面接触线离散点法向柔度矩阵F。
本文面齿轮传动大、小轮齿面均采用作者在文献[23]中所述的碟形砂轮磨齿展成,获得齿面(包括过渡曲面)离散点后,考虑齿轮轮缘并根据面齿轮副几何特点编程生成节点和单元,图1所示为生成面齿轮有限元模型。
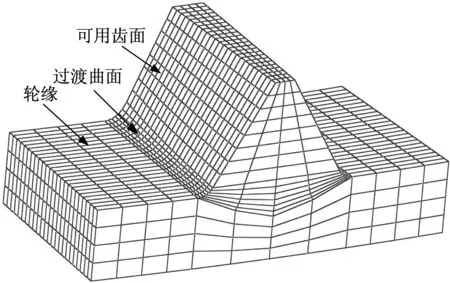
图1 面齿轮有限元模型
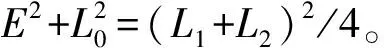
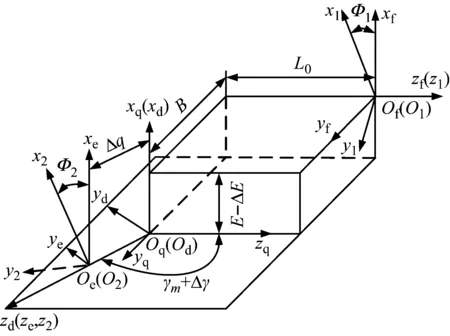
图2 啮合坐标系
(1)
式中:R1f、n1f为小轮位矢和法矢,u1、l1是展成小轮齿面的独立参数;R2f、n2f为面齿轮位矢和法矢,u2、l2是展成面齿轮齿面的独立参数。
上式可分解得含6个参数5个独立的标量方程,以一定增量ΔΦ2=2π/(z2N) (N为啮合周期等分数)改变Φ2值输入即可求解得到啮合迹线,并根据下式求解几何传动误差
ΔΦ2=Φ2-Φ20-z1/z2(Φ1-Φ10)
(2)
式中:Φ10、Φ20是两齿面初始转角,z1、z2是两轮齿数。
不考虑轮齿啮合时的润滑油和摩擦力作用,则在总法向啮合力P作用下,面齿轮传动承载接触分析的模型如图3所示。面齿轮传动为准共轭点接触齿面,在载荷作用下轮齿将产生弹性变形,不计瞬时接触区宽度,认为点接触将扩展为沿瞬时接触椭圆长轴发生的线接触。图中表示的即为齿面过瞬时接触椭圆长轴的法截面,假设有齿对I和齿对II可能同时接触,接触椭圆中心为i点,而j点为接触椭圆长轴上的任意离散点(2对齿间共n个离散点),则变形后位移协调方程为
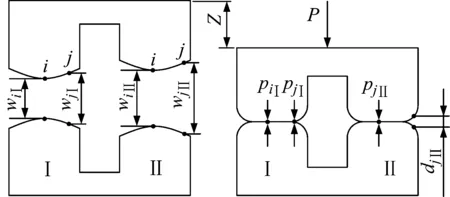
图3 面齿轮传动承载接触模型
Fkpk+wk=dk+Zk(k=I,II)
(3)
式中:pk=[p1,p2, …,pn]T为瞬时接触椭圆长轴离散点处法向载荷;dk=[d1,d2, …,dn]T为瞬时接触椭圆长轴离散点处变形后的齿面间隙;Zk=Z[1, 1, …, 1]T为轮齿变形后的法向位移。
各离散点法向载荷pj(j=1, 2, …,n)须满足力平衡条件
(4)
轮齿接触时非嵌入条件为
(5)
根据前述内容,综合考虑了齿面修形、变位、小轮偏置以及安装误差等因素的面齿轮传动承载接触问题的数学规划表示如下
(6)
上述非线性规划目标为变形能最小,Xj(j=1, 2,…,n+1)为人工变量;X=[X1,X2, …,Xn]T,n维列向量;e为单位n维列向量;pj≥0、dj≥0、δj≥0、Xj≥0为接触边界条件。用改进的正规形法[24]求解上式,由此获得未知参数d、Z、p,并下式计算齿对I和II在某任意瞬时啮合位置的载荷分配系数
(7)
齿轮传动误差的定义为“主动轮转过一定角度,从动轮实际转动位移与理想转动位移之差”[25],故可将面齿轮轮齿变形后的法向位移按下式转换为承载传动误差
(8)
式中:ω2为面齿轮角速度矢量。
图4所示为按上述方法获得的典型面齿轮传动修形后的几何传动误差TEG和承载传动误差TEL曲线,几何传动误差曲线上的点a和a′为单齿啮合与双齿啮合的临界转换点,距离aa′ 即为一个啮合周期T,几何传动误差曲线下端开口距离cc′ 与啮合周期T之比即为面齿轮传动的有效重合度。承载后的实际重合度由几何传动误差曲线和承载传动误差曲线的交点b和b′确定,等于距离bb′ 与啮合周期T之比,点b和b′即为啮入和啮出点。无载时实际重合度为1,即几何传动误差曲线应为连续的实线部分。在某任意瞬时啮合位置,承载后的轮齿法向综合变形量δ取决于TEG-TEL的大小,两者按下式转换
(9)
单齿副啮合刚度是指只考虑一对主动轮齿和被动轮齿从进入啮合到退出啮合的刚度,综合啮合刚度是指整个啮合周期内所有参与啮合的多对轮齿啮合刚度叠加后的综合效应。设单对轮齿在啮合周期T内共有8个啮合位置,从进入啮合到退出啮合共有N个啮合位置,则面齿轮传动综合啮合刚度和单齿副啮合刚度分别由式(10)和式(11)计算
(10)
ks(jj)=km(jj-8floor(jj-1)/8))Lk(jj)(jj=1,2,3,…,N)
(11)
根据上述内容,将面齿轮传动啮合刚度求解程序化,流程见图5,整个过程求解耗时仅约5 min。

图5 啮合刚度求解流程
2 计算精度验证
目前,由于面齿轮传动啮合刚度尚未有比较权威的计算方法和公式,而渐开线圆柱齿轮的啮合刚度计算方法已较成熟,并有不少文献给出了相关的计算方法和公式。为验证本文所提出基于LTCA的啮合刚度计算方法的可行性和精确性,现采用本文方法和现有文献方法分别对斜齿轮传动的综合啮合刚度进行计算。Maatar等[26]基于齿轮副瞬时接触线长度,推导出简单实用的斜齿轮综合啮合刚度解析式,并得到了较广泛应用,具体公式如下
(12)
式中:k0,Lk,Ak,Bk,τ具体含义见文献。
斜齿轮传动基本几何参数:大、小轮齿数为41、40,法向压力角为20°,分度圆螺旋角为14°27′24″,法向模数为4 mm,齿顶高系数为1,顶隙系数为0.25,齿宽为30 mm。齿轮材料弹性模量为206 GPa,泊松比为0.29,负载为10 000 N·m。上述2种方法计算结果见图6,可见2种方法计算所得综合啮合刚度曲线变化规律比较吻合,但因式(12)未考虑齿轮齿根过渡曲面和轮缘变形对啮合点影响,导致其结果偏大,但最大偏差为8.92%,平均偏差仅为5.83%,故采用本文方法分析面齿轮传动啮合刚度可以保证较高精度。
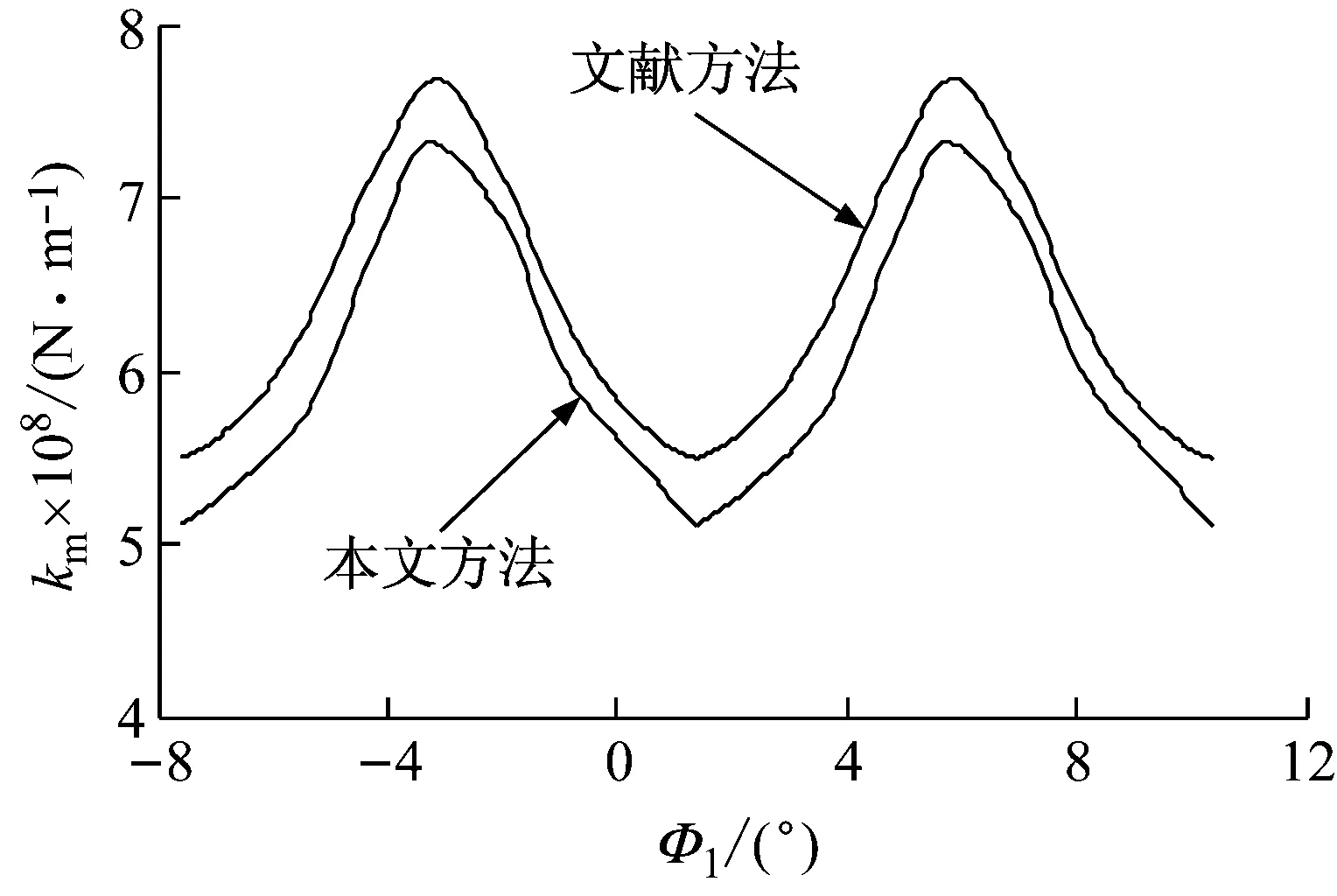
图6 综合啮合刚度比较
3 面齿轮传动啮合刚度分析
某偏置变位面齿轮传动仿真参数如下:面齿轮产形轮齿数为31,面齿轮齿数为140,面齿轮内径、外径分别为425 mm、465 mm,直齿圆柱小轮齿数为28,模数为6.35 mm,压力角为25°,变位系数为-0.2,小轮偏置距为50 mm,轮缘系数为2.5,轴夹角γ为90°,小轮齿条刀和面齿轮产形轮的刀顶圆弧半径均为0.635 mm。面齿轮传动的材料参数与前述斜齿轮传动相同。
图7、图8、图9分别负载为1 000 N·m时的法向变形量、啮合刚度、单对轮齿从进入啮合到退出啮合过程中法向啮合力的变化曲线。由图可知,面齿轮传动综合啮合刚度和法向变形量的波动表现出较明显的阶跃突变,这是因为该变位偏置面齿轮传动重合度约为1.5,啮合过程存在“双齿—单齿—双齿”交替变化,在双齿啮合区,整个载荷是由两对轮齿共同承担的,故此时齿轮的法向变形量较小,而综合啮合刚度较大,反之,在单齿啮合区,整个载荷仅由一对轮齿承担,故此时齿轮的法向变形量较大,而综合啮合刚度较小。小轮转角在-8.035°时齿轮副开始进入啮合,随着转角增大,作用在该对轮齿上的法向啮合力逐渐增大,单齿副啮合刚度也逐渐增大;当小轮转角在0°~3.21°时,此时为单齿啮合区,载荷全部作用在该对轮齿上,其法向啮合力达到最大并保持不变,但此区间法向变形量略微增加,故单齿副啮合刚度略微减小;随即下对轮齿进入啮合,该对轮齿上的法向啮合力突变减小,对应的单齿副啮合刚度也以较大幅度减小,之后,该对轮齿上的法向啮合力和单齿副啮合刚度均逐渐减小,直至该对轮齿退出啮合。
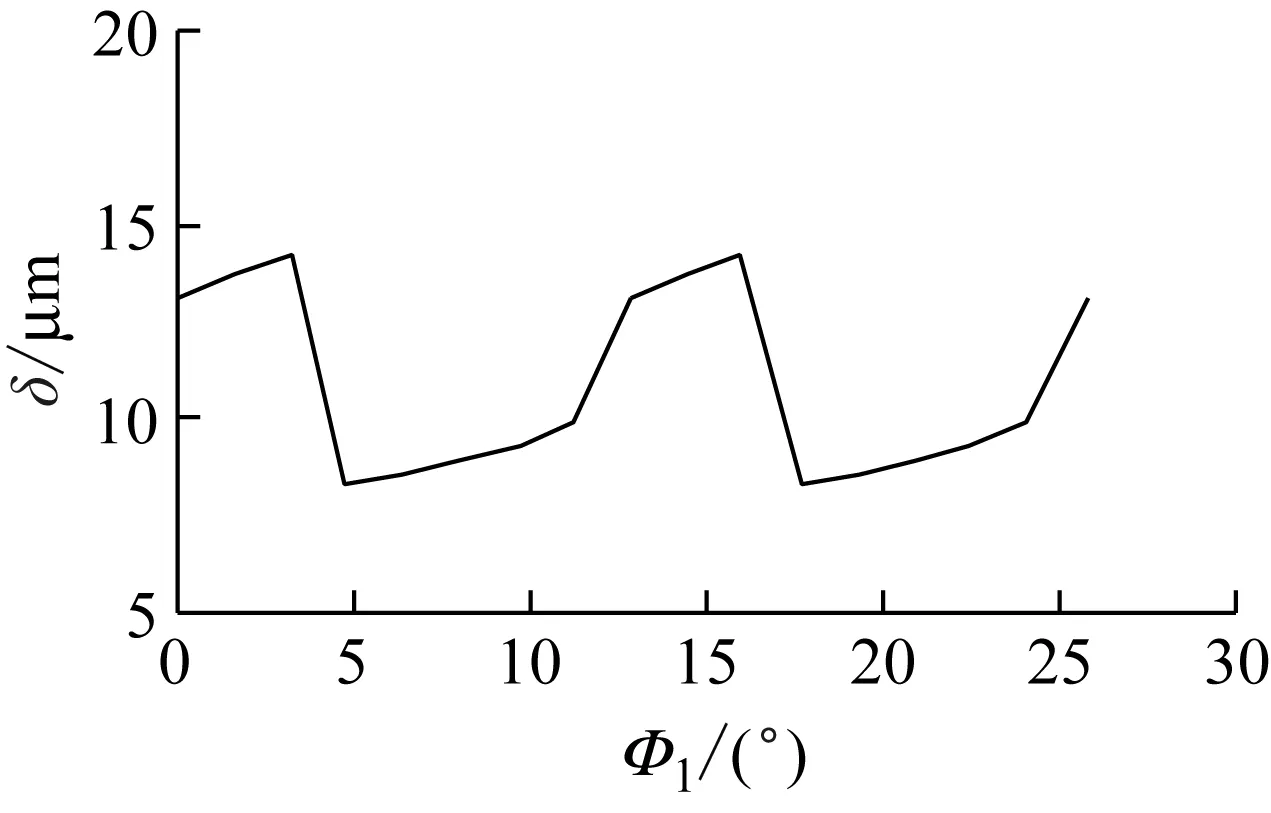
图7 法向变形量

图8 啮合刚度

图9 法向啮合力
为分析负载PL、变位系数x、小轮偏置距E和3类安装误差(轴向位移误差Δq、偏置误差ΔE、轴夹角误差Δγ)对面齿轮传动啮合刚度均值和波动幅值的影响,分别以各单一影响因素作为变量计算面齿轮传动综合啮合刚度,计算结果见图10~图13。
由图可见,综合啮合刚度波动幅值对载荷、变位、小轮偏置和安装误差均不敏感,但综合啮合刚度均值受载荷、小轮偏置和安装误差影响较大。综合啮合刚度均值随载荷增大而增大,随偏置距增大而减小,而几乎不受变位影响。在3类安装误差中,轴夹角误差对综合啮合刚度均值影响最大,而偏置误差对综合啮合刚度均值影响较小,故面齿轮实际安装时要严格控制轴夹角误差。
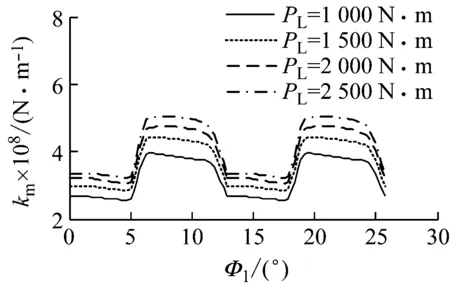
x=0, E=0, Δq=0, ΔE=0, Δγ=0°
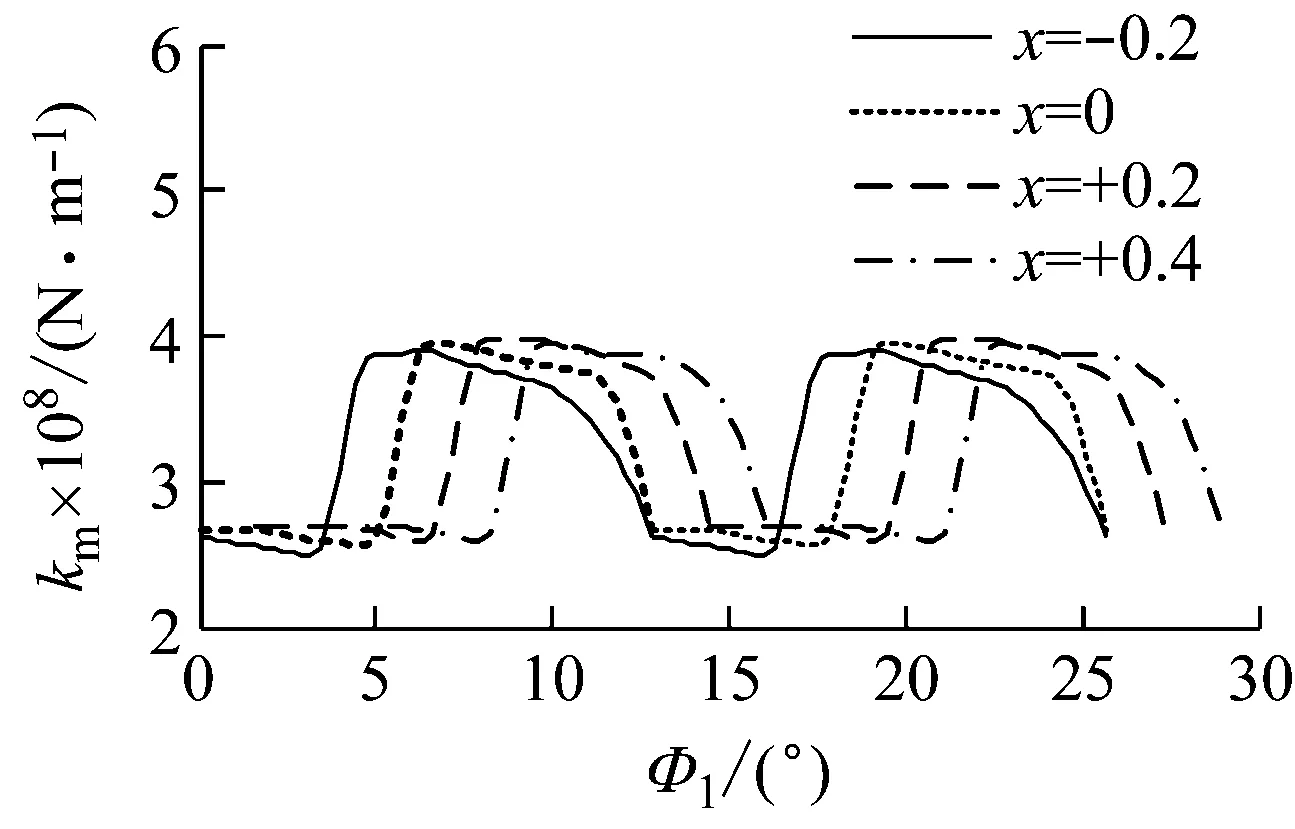
PL=1 000 N·m, E=0, Δq=0, ΔE=0, Δγ=0°
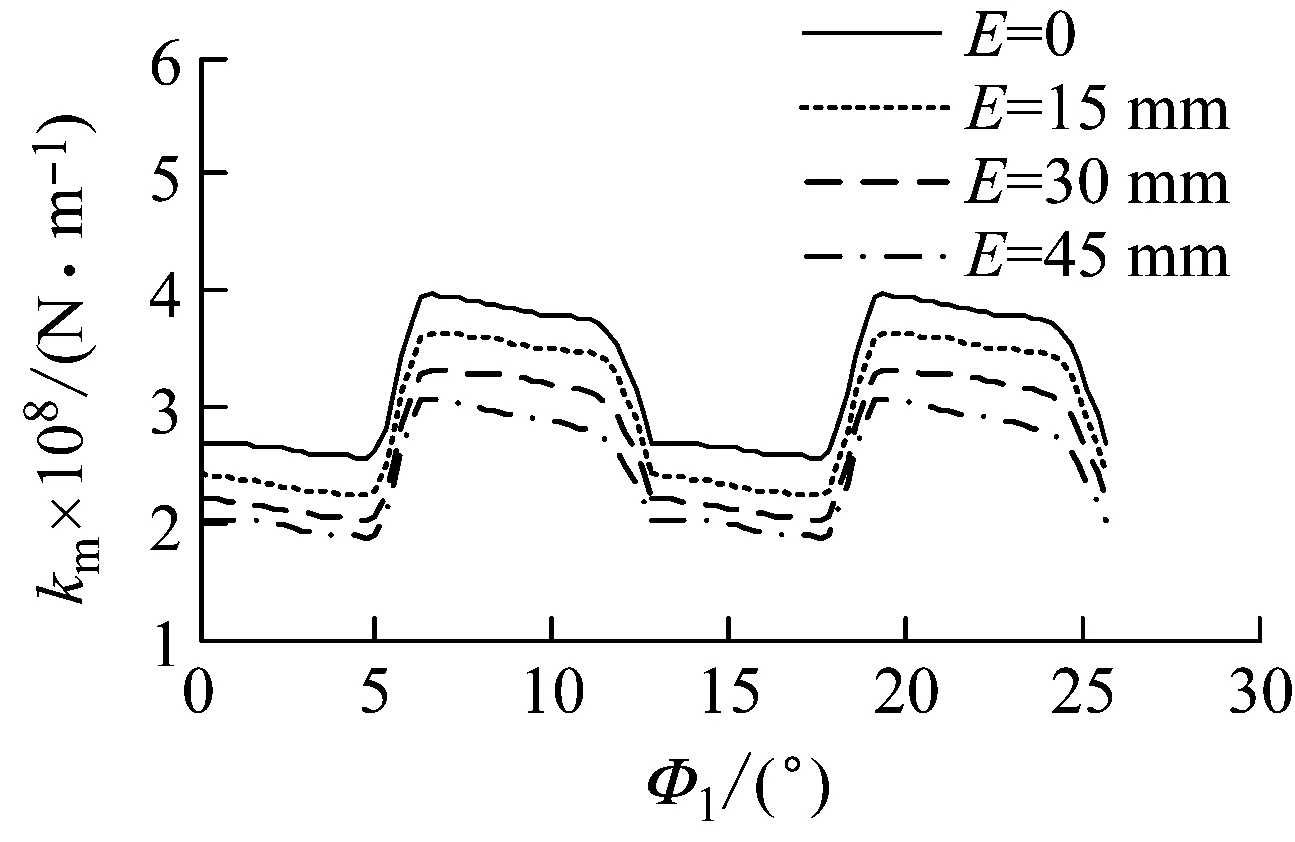
PL=1 000 N·m, x=0, Δq=0, ΔE=0, Δγ=0°

(a) PL=1 000 N·m, x=0, E=0, ΔE=0, Δγ=0°
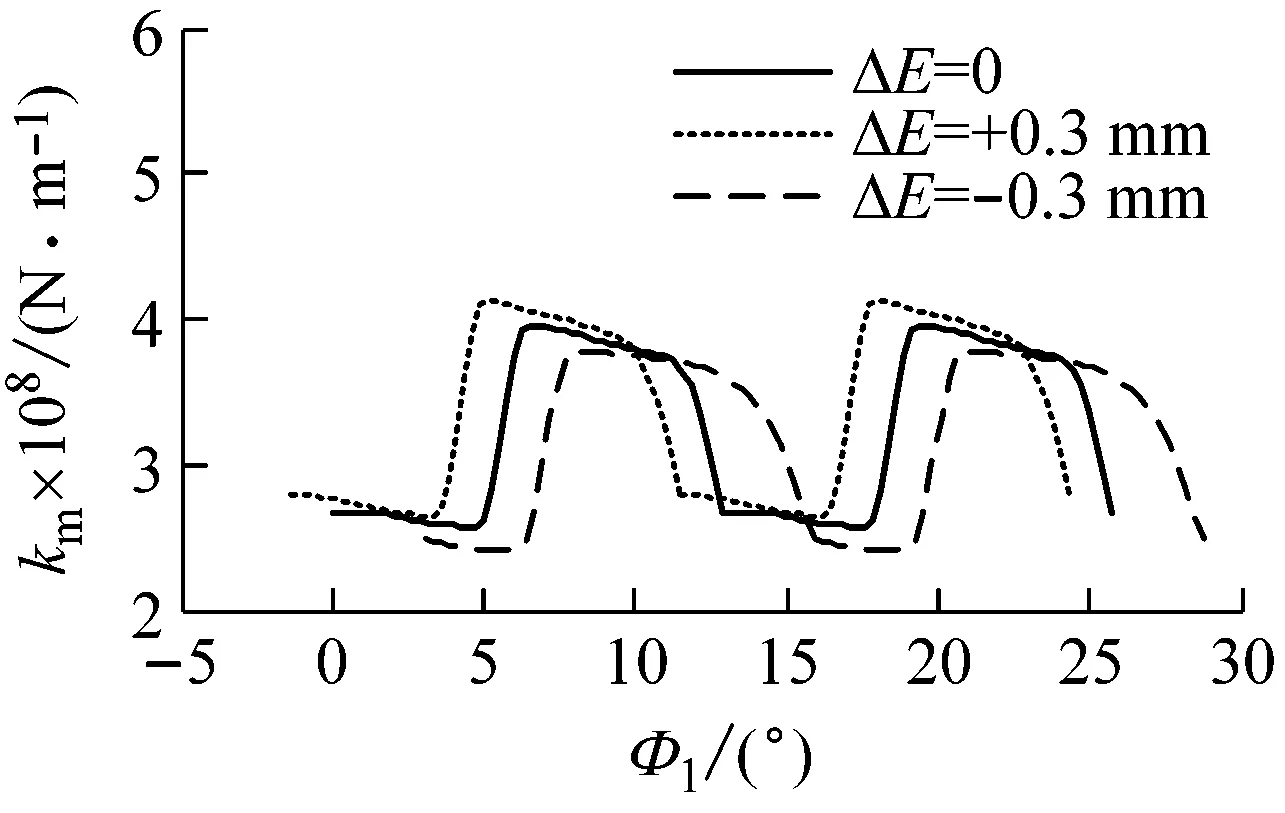
(b) PL=1 000 N·m, x=0, E=0, Δq=0, Δγ=0°
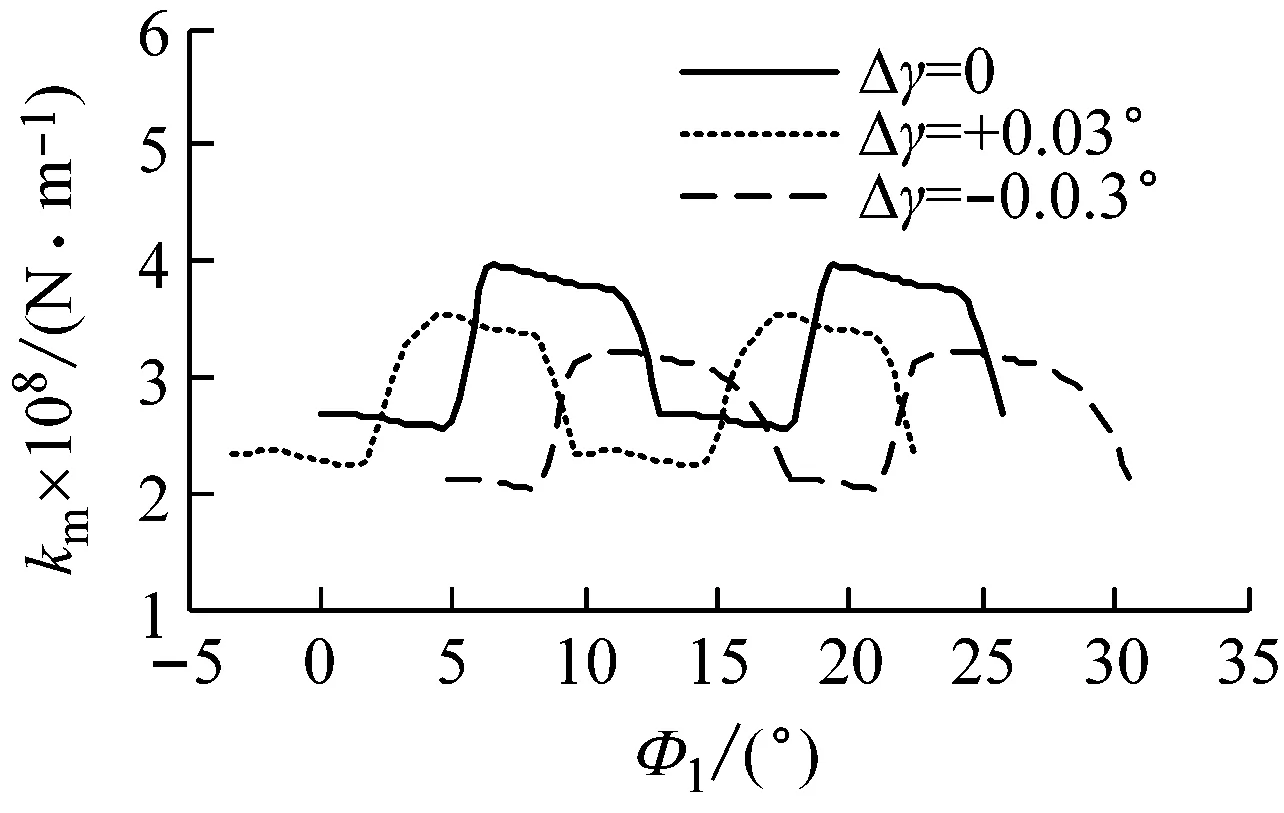
(c) PL=1 000 N·m, x=0, E=0, Δq=0, ΔE=0
4 面齿轮传动修形减振优化
4.1 优化模型
齿轮副的综合啮合刚度变化是产生振动与噪声的主要原因之一,综合啮合刚度变化波动幅值越大,振动越大,噪声越大,变化幅值小则传动平稳[27-28]。齿轮修形技术是齿轮传动减振降噪的重要手段[29],而修形参数选的是否合理,直接决定着能否有效提高承载能力和传动平稳性。通常,面齿轮副大、小轮均可进行修形,但面齿轮齿面复杂、修形难度大,效率低,而小轮齿数少、加工方便,效率高,故在小轮上进行修形更有优势。作者在文献[30]中设计了由2段抛物线与1段直线组成的小轮齿廓、齿向修形曲线,见图14,且修形后啮合性能改善明显。图中l1、l3为齿廓修根时修形量、修形长度,l2、l4为齿廓修缘时修形量、修形长度,l5、l7为齿向两端修形量,l6为齿向不修形长度,h、b为旋转投影面上的齿高、齿长。
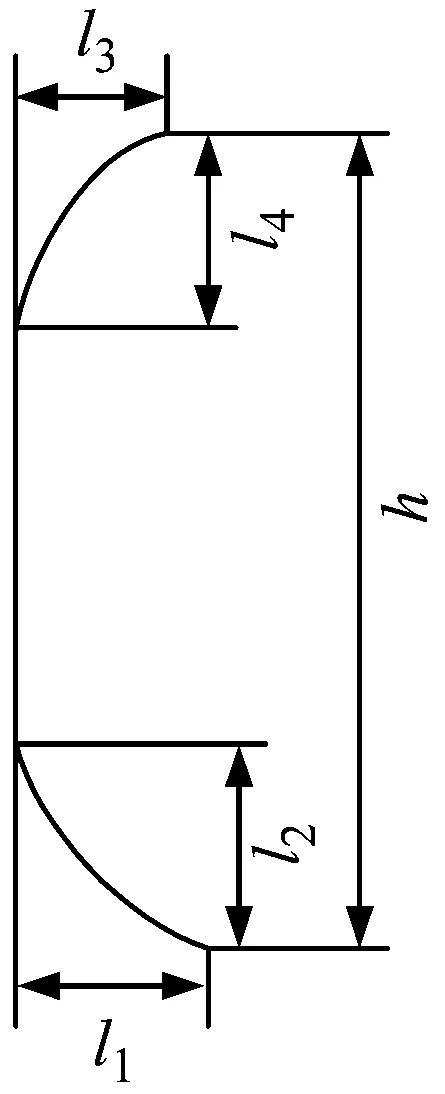
(a) 齿廊方向
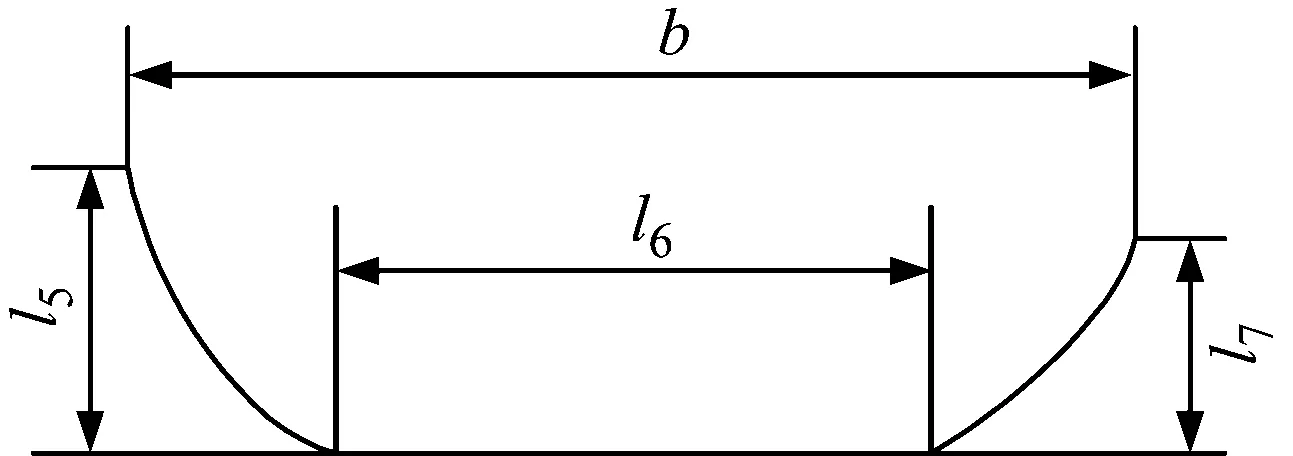
(b) 齿向方向
以上述7个修形参数为优化变量,以综合啮合刚度波动幅值最小为目标,则面齿轮传动修形减振优化模型可简化如下。
优化变量:l1、l2、l3、l4、l5、l6、l7;
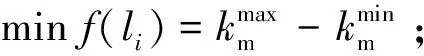
根据前述齿轮参数和拓扑修形工艺要求,优化变量取值范围见表1。
4.2 优化算法
本文优化过程是通过不断改变小轮的修形参数,来改变齿面接触状况的迭代过程,属高度非线性接触问题。优化变量与目标函数之间无直接关联,无法建立两者的解析表达式,现采用带有精英策略的快速非支配排序遗传算法(NSGA-Ⅱ)求解上述优化模型,流程见图15。NSGA-II算法参数[31]取值如下:交叉、变异概率取0.9、0.1,为节省时间,终止进化代数gmax=50,种群规模取20。

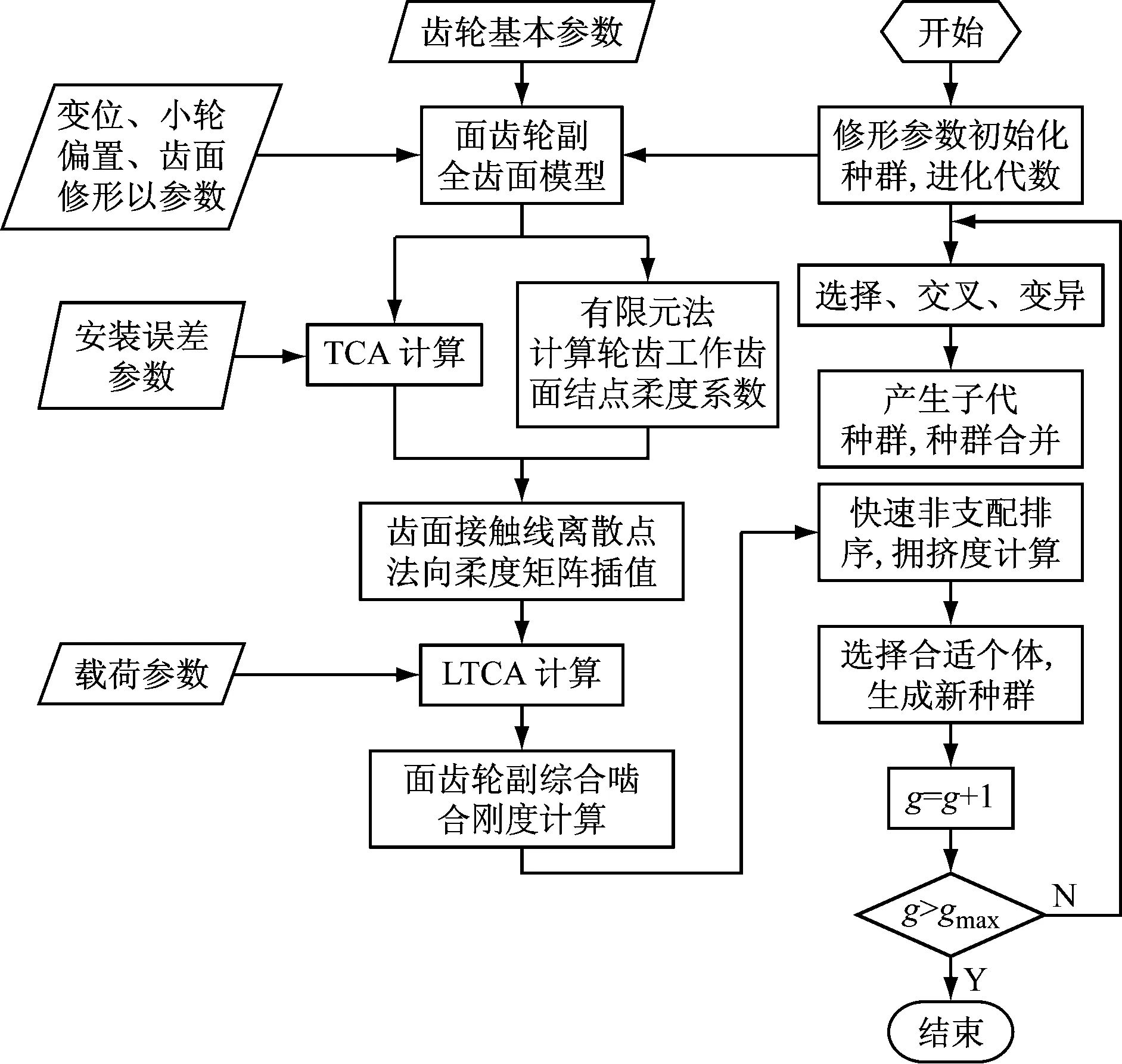
图15 NSGA-Ⅱ算法修形减振优化流程
4.3 优化结果与讨论
图16所示为未修形面齿轮传动和修形减振优化后面齿轮传动对应的综合啮合刚度,优化获得的变量取值如下:l1为0.015 mm、l2为5.660 mm、l3为0.010 mm、l4为5.315 mm、l5为0.017 mm、l6为22.506 mm、l7为0.018 mm。由图可见,优化后齿面拓扑修形虽使综合啮合刚度的均值稍有减小,但综合啮合刚度的波动幅值大幅下降,由1.391×108N/m降为0.124×108N/m,减小了91%,故优化修形参数可有效减小面齿轮传动的振动和噪声。

PL=0, x=0, E=0, Δq=0, ΔE=0, Δγ=0
5 结 论
(1) 综合考虑变位、小轮偏置、齿面修形以及安装误差,提出了基于LTCA技术的面齿轮传动啮合刚度计算方法,并将斜齿圆柱齿轮传动的啮合刚度计算结果与文献对比,验证了本文方法的精确性。
(2) 对某变位偏置面齿轮传动的分析表明,面齿轮传动的法向变形、啮合刚度和法向啮合力随啮合位置变化,且波动幅值较大,存在阶跃突变现象。
(3) 载荷、变位、小轮偏置和安装误差对面齿轮传动综合啮合刚度均值和波动幅值的影响分析表明,综合啮合刚度波动幅值对载荷、变位、小轮偏置和安装误差并不敏感,但综合啮合刚度均值受载荷、小轮偏置和安装误差影响较大;在3类安装误差中,轴夹角误差对综合啮合刚度均值影响最大,故面齿轮实际安装时要严格控制轴夹角误差。
(4) 优化小轮修形参数后使综合啮合刚度的波动幅值大幅下降,从而可有效减小面齿轮传动的振动和噪声。

