地铁隧道与人防地下室相互作用的地震反应分析
毛昆明, 赵 凯, 朱利明, 左 熹, 陈 磊
(1.金陵科技学院 建筑工程学院,南京 211169;2.南京工业大学 岩土工程研究所,南京 210009;3.中国联合工程有限公司,杭州 310052)
进入21世纪以后,中国城市地下空间的开发数量快速增长,城市地下结构体系不断完善,但也导致地下结构群之间产生相互影响的问题突出。以地铁为代表的地下结构空间交叉条件下的地震反应特性和上下结构之间的相互作用效应复杂,影响因素众多,针对个案仍有待于进一步的深入研究[1-3]。
陈磊等[4]数值分析了双层不同角度交叉隧道的地震反应特性,双层隧道的相互作用效应对上、下层隧道顶、底部之间的相对水平位移差具有放大作用,对上、下层隧道的地震应力反应有减小作用。胡建平等[5]数值分析了浅埋交叉隧道的地震反应,发现最大位移常出现在上部隧道的交叉部位,最大主拉应力一般出现在下部隧道出口顶部,最大主压应力通常发生在上部隧洞顶板与边墙连接处。李积栋等[6-8]先后数值分析了密贴交叉组合地铁地下车站结构的三维非线性地震反应特性,并与单一地铁车站的地震反应特性进行了比较,结果表明密贴交叉组合车站中上/下层车站的相对水平位移均大于单一浅/深埋地铁车站;后建下穿地铁车站结构对先建地铁地下结构相对水平位移有明显的放大效应。Liang等[9]利用间接边界元法研究了半空间中双无穷长隧道在SH波作用下的反应,发现当两个隧道接近时,其表面位移峰值会显著放大。Fang等[10]利用半解析方法对P波下紧密间隔的双隧道的之间的相互作用所产生的自然危害进行了评估,并对不同界面条件下的隧道相互作用进行了数值分析,得到了其动态应力集中和位移分布。Alielahi等[11]利用时域边界元法分析了两个平行隧道对地面地震反应,结果表明双隧道的深度和间距以及入射波的波长对地表的放大模式有重要影响,并给出了放大系数,在此基础上对建筑规范中标准设计谱的修改提出了设想。Wang等[12]对地下车站与临近建筑的桩基础在垂直入射波下的动力相互作用进行了数值研究,分析了位置关系、距离、地震波方向、土性、埋深、刚度的影响,发现结构之间的位置关系和地震波方向起决定性作用。
综上所述,大部分学者仅考虑了双层或双向地铁隧道的相互影响作用,且没有考虑混凝土塑形变形影响,笔者尚未见到考虑地铁隧道与附近其它地下建筑结构相互作用的弹塑性地震反应分析。
南京地铁4号线鼓楼站西侧为鼓楼公园,鼓楼公园下方有一人防地下室,公园环岛中间的明代高台基木结构鼓楼为省级保护文物。区间隧道和人防地下室距离很近,在地震作用下由于相互作用可能会使反应增大,甚至可能会加剧上部古建筑在地震作用下的破坏程度。
本文以自行研发的Abaqus软件64CPU显式并行计算集群为平台[13],以南京地铁4号线鼓楼站的附近的地下建筑结构为工程背景,建立了深软地基土-地铁隧道-人防地下室耦合的三维精细化非线性地震反应分析的有限元模型,数值模拟了其在近场汶川大地震清平波、远场大地震Mexico波和100a超越概率3%的南京人工地震波作用下的地震反应。
1 有限元模型
1.1 计算模型的建立
人防地下室墙体及隧道衬砌均用壳单元模拟,图1为二者的形状。人防地下室年代久远,壁厚0.45 m,根据前期检测结果,混凝土强度推定值为46.3 MPa。隧道横截面为“五心圆形”,衬砌厚0.35 m。
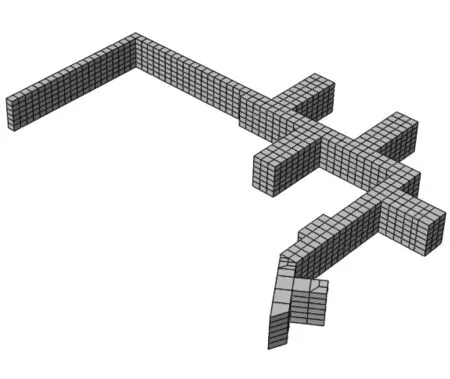
人防地下室
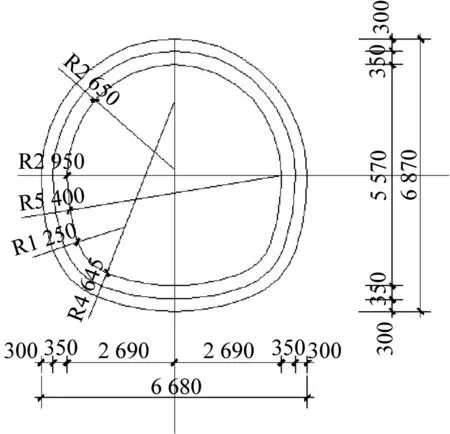
隧道横截面(mm)
人防地下室的上覆土层厚8 m,左隧道的上覆土层厚14 m,右隧道的上方地表为一斜坡,平均上覆土层厚8.7 m,人防地下室与隧道竖直距离0.57 m,最近水平距离7.7 m,模型具体尺寸及网格划分见图2。为了获得较为精确的模拟结果,模型采用精细化建模方式,共建单元503 063个。其中,土体单元492 579个,人防单元1 934个,隧道衬砌单元8 550个,均采用减缩积分。

图2 有限元模型(m)
隧道及人防地下室与土法向采用硬接触,切向采用罚函数摩擦接触,摩擦因数0.3。垂直于输入地震波方向的地基土侧面设置竖向约束、水平向施加谷音等[14]提出的加弹簧阻尼器的黏弹性人工边界,平行于输入地震波方向的地基土侧面约束竖向位移,底部基岩面为水平向地震波输入界面。
图3为人防地下室与隧道的相对水平位置图,选取有代表性的隧道的7个横断面以及人防地下室的7个关键部位进行重点分析。
采用Lee等[15]提出的C50混凝土的黏塑性动力损伤模型,具体参数参见文献[4],用损伤值描述地震损伤程度。损伤值介于0和1之间,0和1分别表示无损伤状态和完全损伤状态。采用陈国兴学术团队开发的土体动力黏弹塑性记忆型嵌套面动力本构模型[16]模拟土的动力特性,具体参数详见表1。
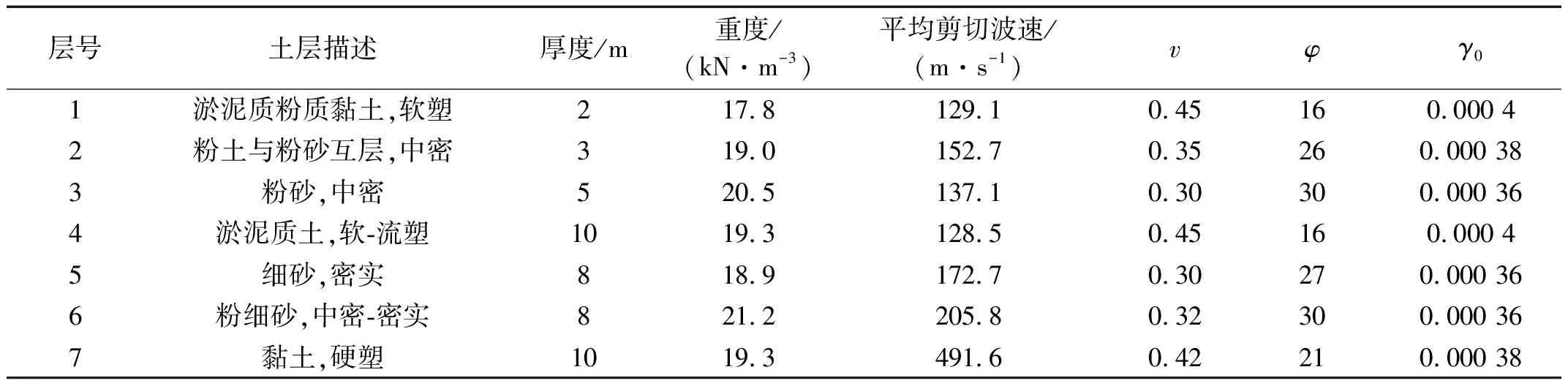
表1 软弱场地的记忆型嵌套面动力本构模型参数

图3 人防地下室与隧道水平位置关系
1.2 地震波选取
南京及周边地区处于中等地震活动区,没有地震记录,因此难以直接利用本地地震记录的统计分析来估计此区域场地的地震反应。本文选取了国内外具有代表性的2条地震动加速度记录作为的近、远场输入地震动。作为比较,另选取100 a超越概率3%的某南京地铁车站基岩人工波,相关的参数见表2。
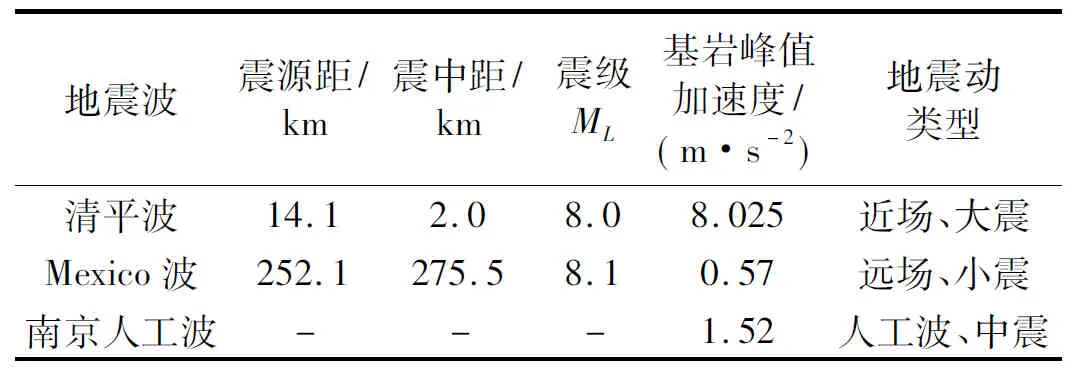
均取含有峰值加速度的前40 s时程进行计算,地震波的加速度时程如图4所示,傅氏谱如图5所示。可以看出,绵竹清平波具有典型大脉冲特征的近场脉冲型地震动,中高频段频谱丰富;而远场地震动Mexico波的低频成分较丰富,10 Hz以上的频谱成分急剧减少;南京人工波(大震)不管是加速度峰值还是频谱成分上都是介于近远场地震动之间的一种“中场”地震动,低频成分的比例较大。
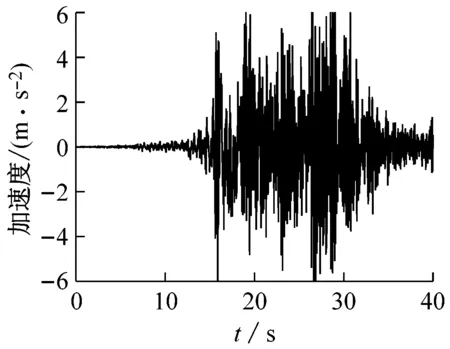
绵竹清平波
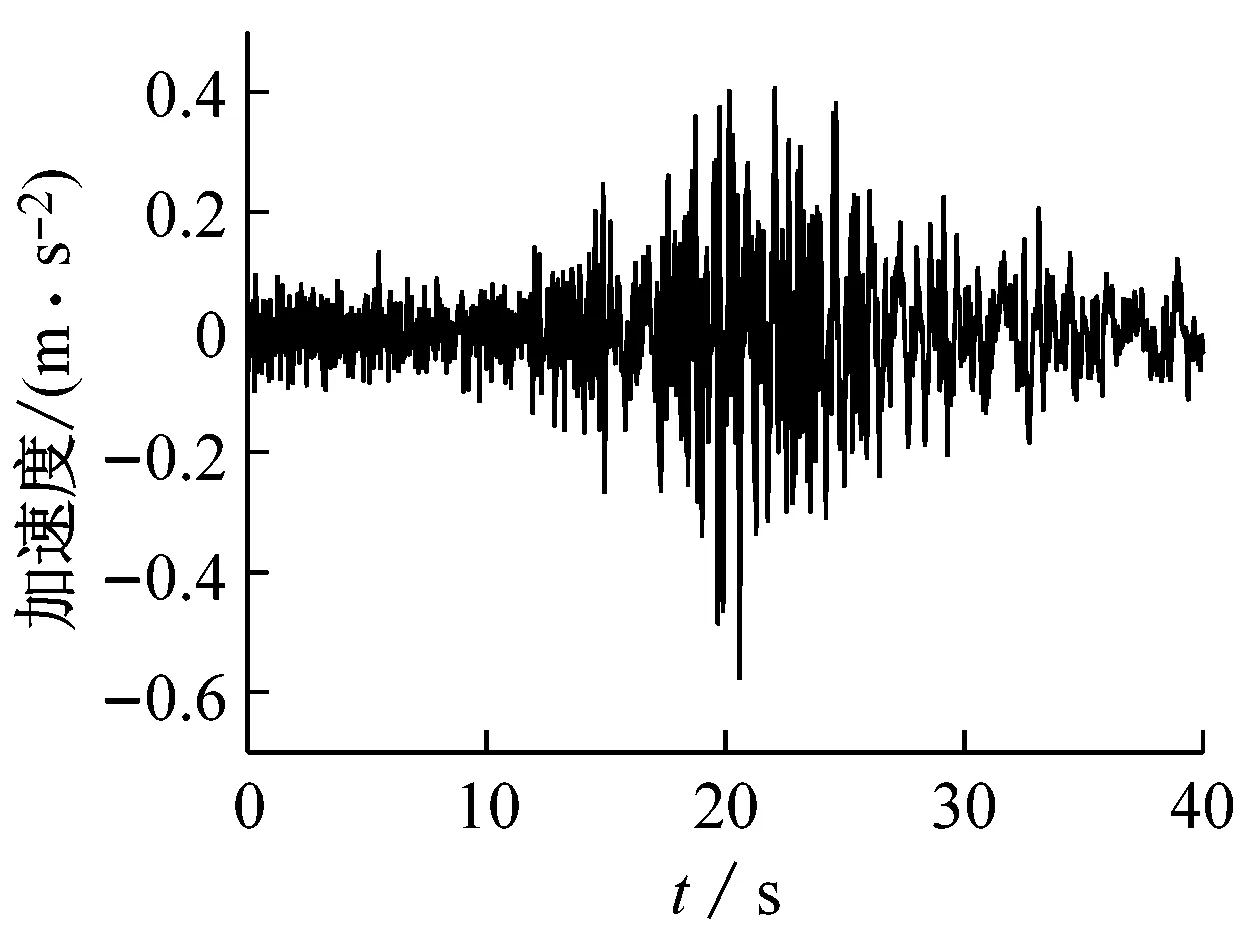
Mexico波

南京人工波
2 计算结果与分析
除图2所示有限元模型外,另建立了只有隧道和只有人防地下室的模型,分别用于2.1节和2.2节的分析。限于篇幅,本文主要分析实际工程中最关心的结构损伤及相对位移。
2.1 地铁区间隧道地震反应分析
图6是不同地震波作用下D-D截面的隧道损伤云图(显示了壳单元厚度),隧道中间数据为损伤值。“五心圆形”隧道拱肩和拱腰的圆弧连接处(图1中a、e点)附近损伤值最大,这与圆形隧道出现在与竖向轴约成45°附近不同。Mexico波作用下除拱肩和拱腰有轻微损伤外,其余部位基本无损伤;清平波作用下损伤范围大,最大损伤值达到0.751 3,丧失约四分之三的承载力,但顶底部未损伤。因此隧道设计时应加强拱肩和拱腰处衬砌强度,但要想抵御罕遇特大近场地震动,需加强更多的部位。

绵竹清平波

Mexico波
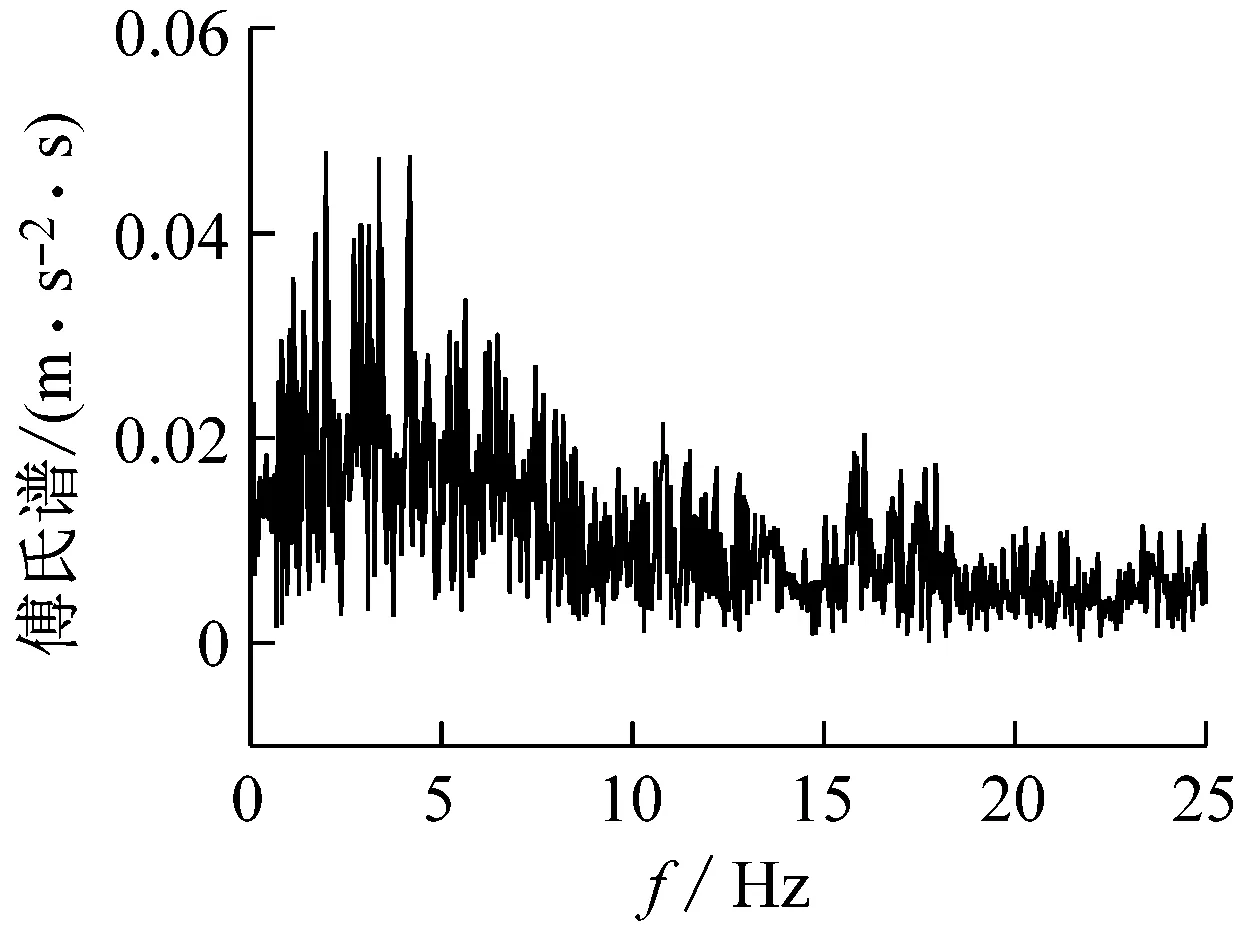
南京人工波
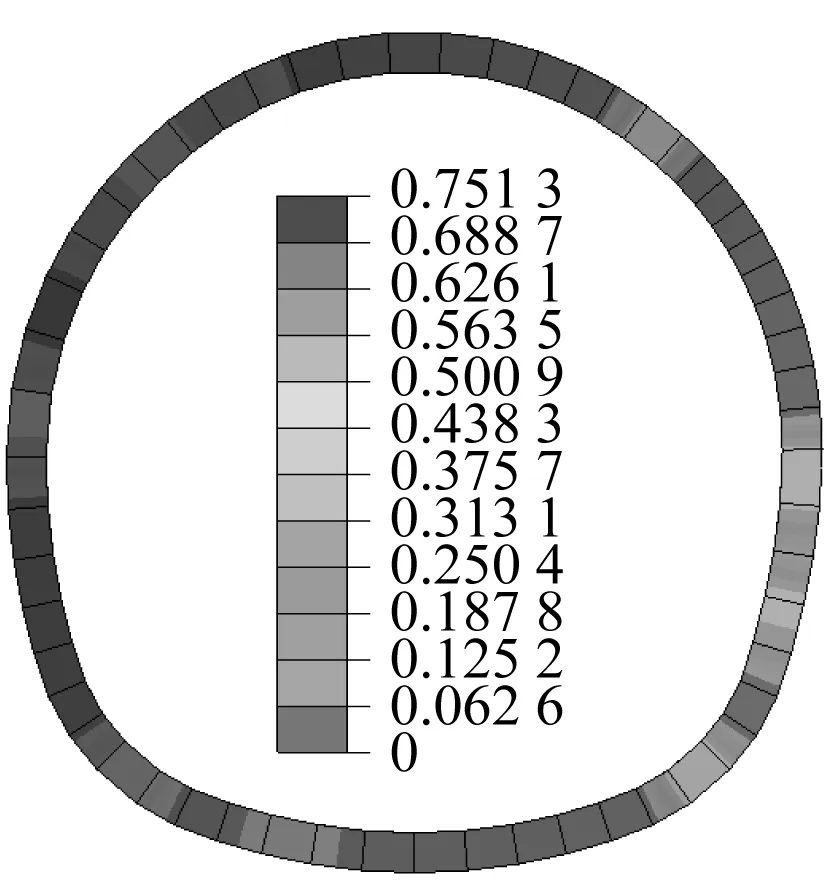
清平波
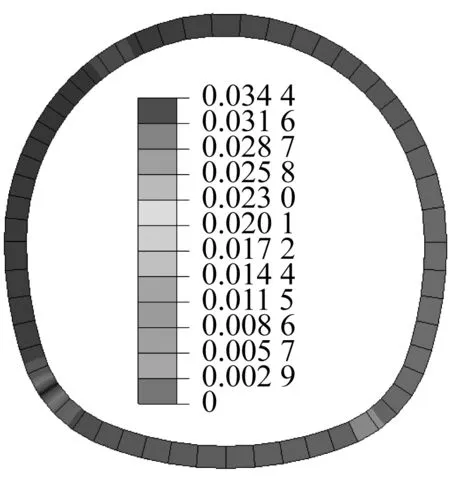
Mexico波
图7是不同地震波作用下的隧道变形及损伤图,黑点是网格节点,隧道中间数据为损伤值。
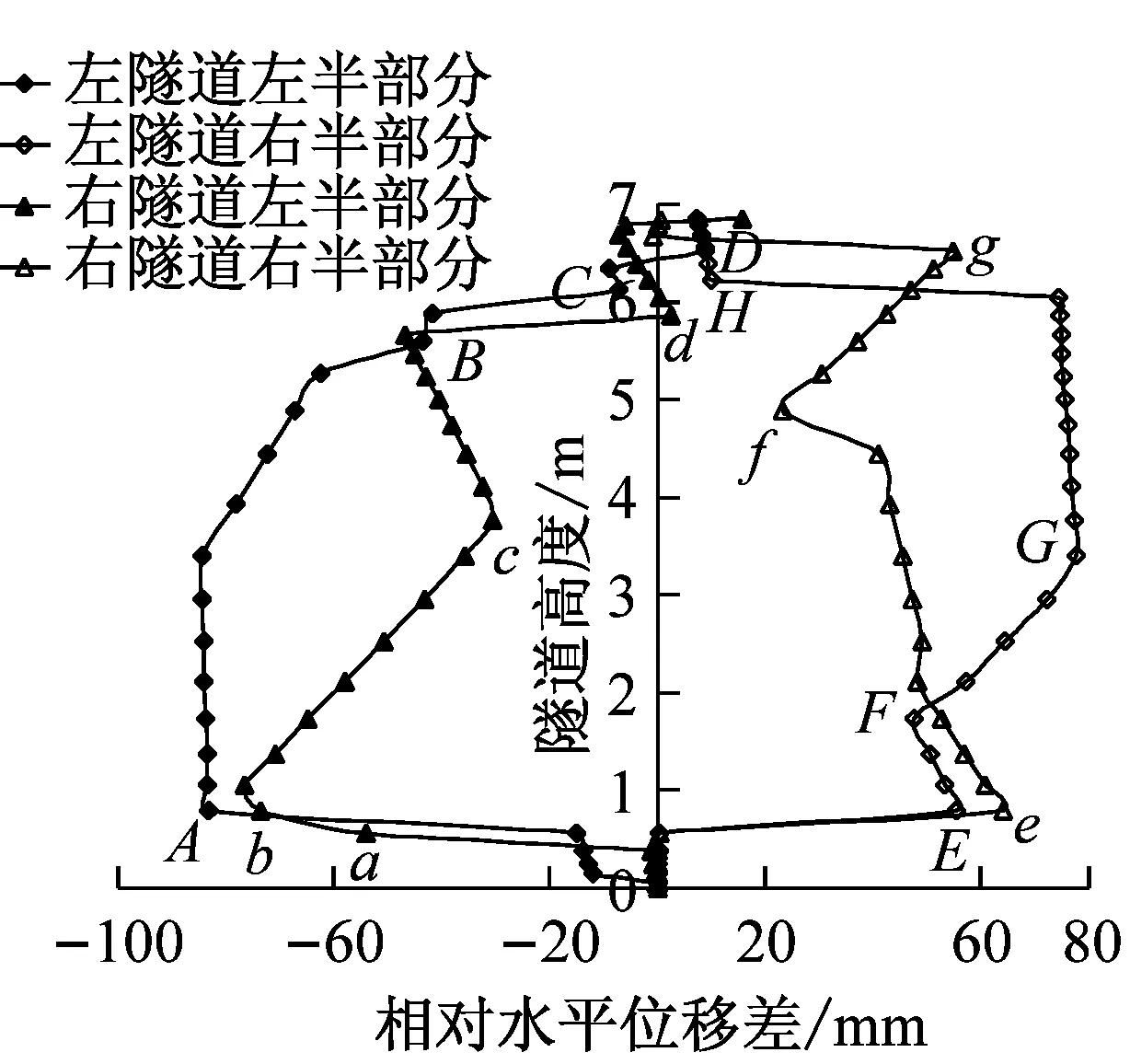
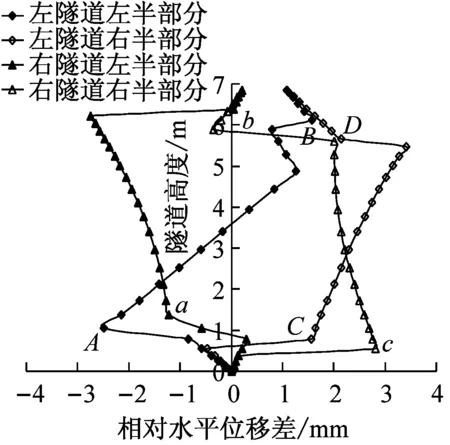
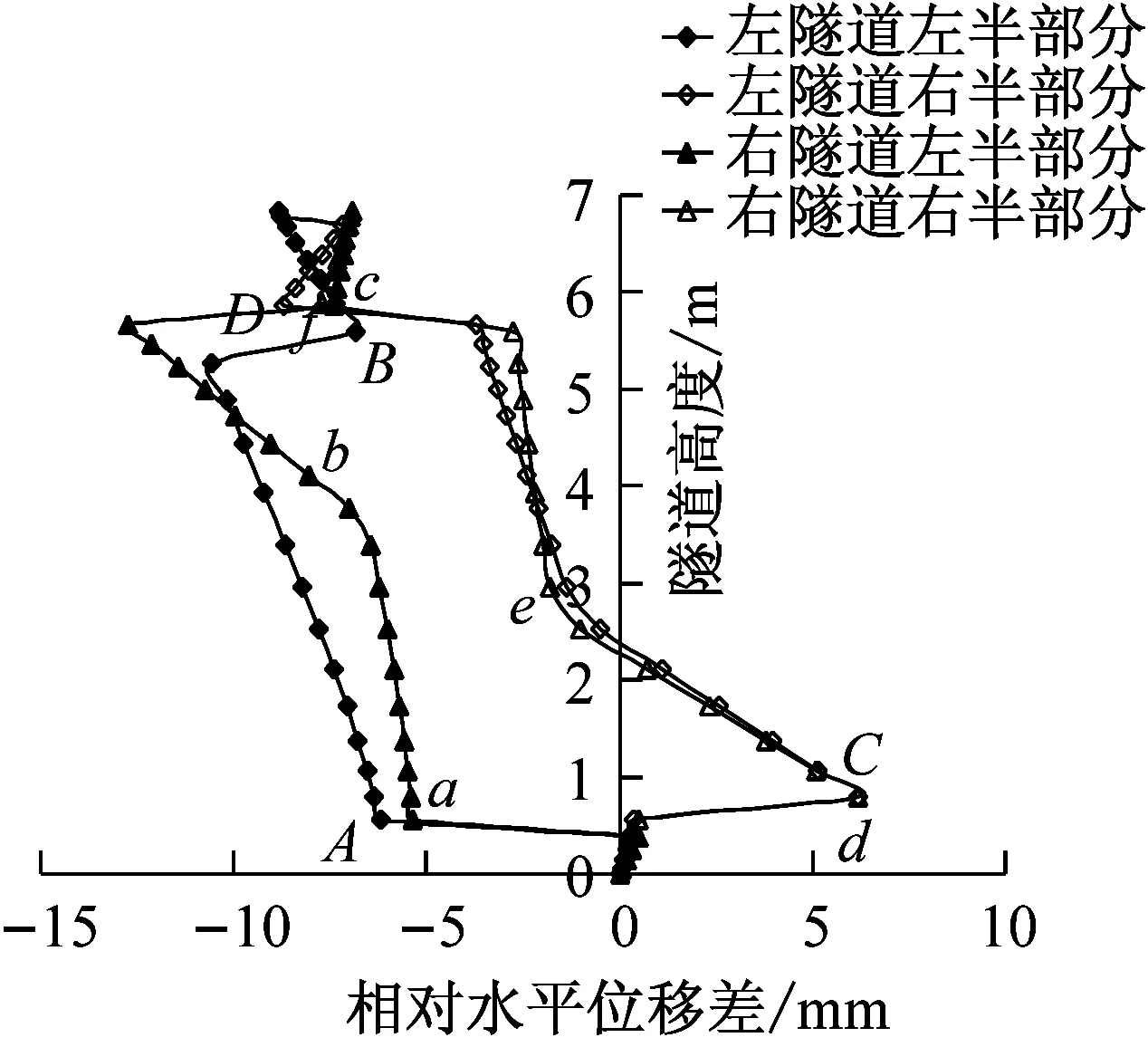
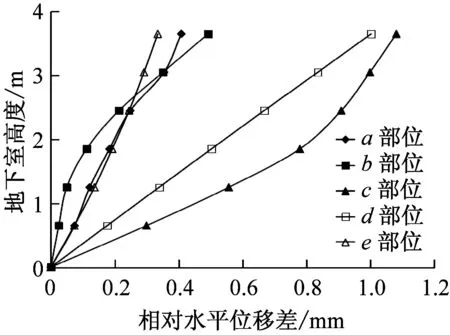
将隧道不同深度处的水平位移幅值与隧道底部水平位移幅值之差定义为隧道的相对水平位移差。图8为不同地震波作用下隧道相对水平位移沿隧道高度的变化曲线。可以看出,隧道的相对位移曲线是由几段直线或光滑曲线连接而成,但在连接处突变,地震波峰值加速度越大,突变点越多,整条曲线形状也越复杂。相对位移的突变点在图中用字母标出,与图7标出的节点对应。可以看出,突变点的损伤值都比较大,即产生了较大的塑性应变,造成局部塑性变形过大。同时对照图1可以看出,突变点正是圆弧连接处附近,尤其清平波作用下几乎所有圆弧连接点附近均产生位移突变。
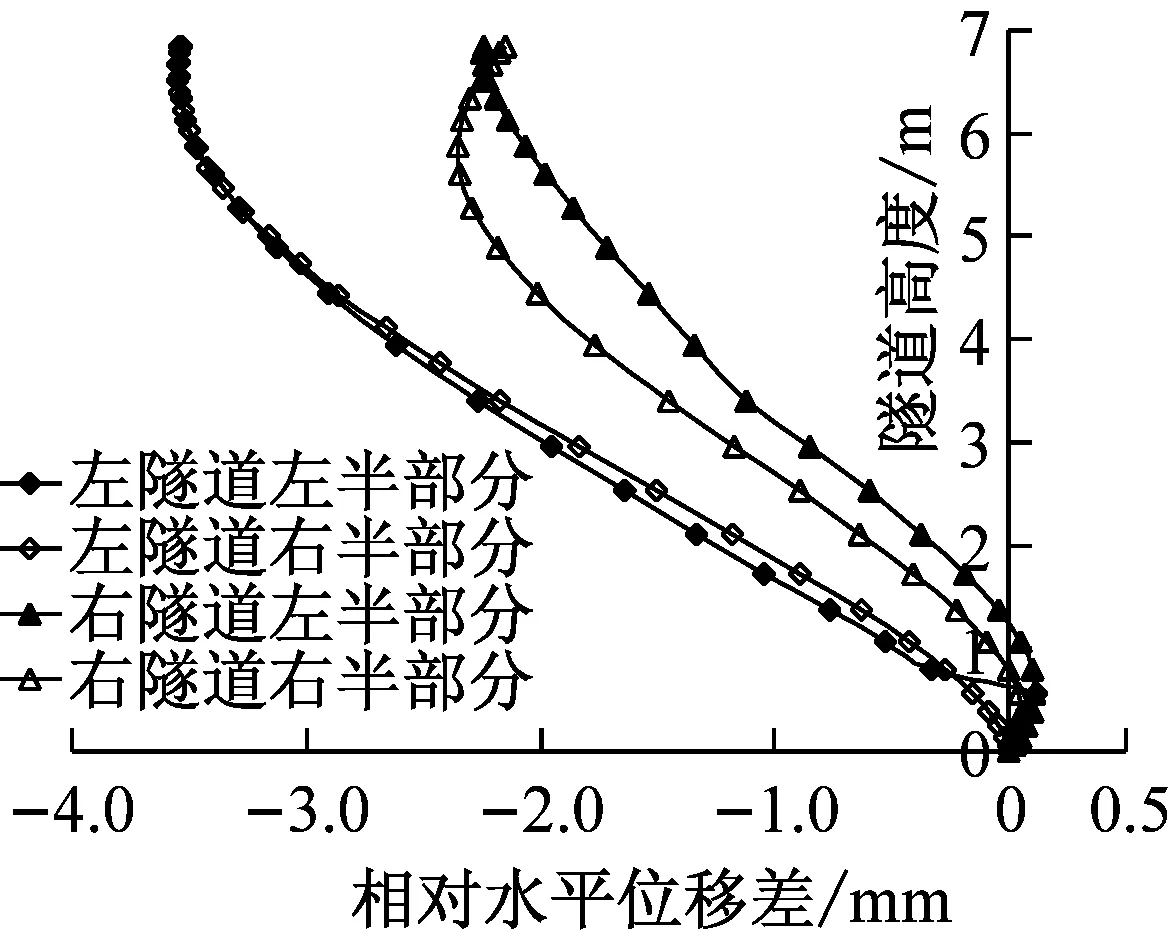
图9是弹性状态下隧道的相对水平位移曲线。曲线呈直线或反S型光滑曲线,从侧面验证了局部塑性变形过大导致相对位移产生突变。
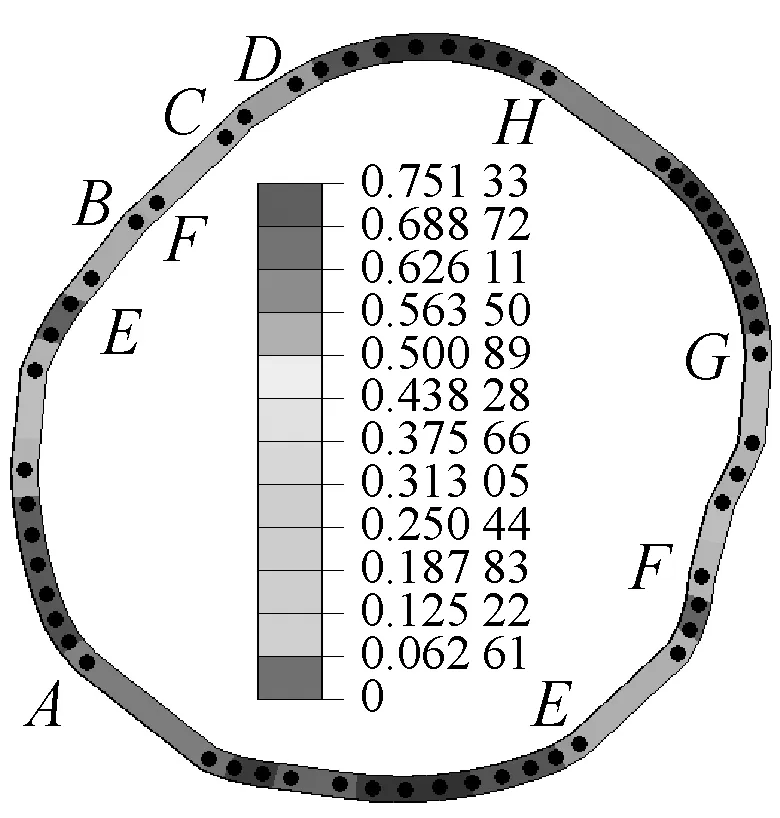
左隧道

右隧道

左隧道
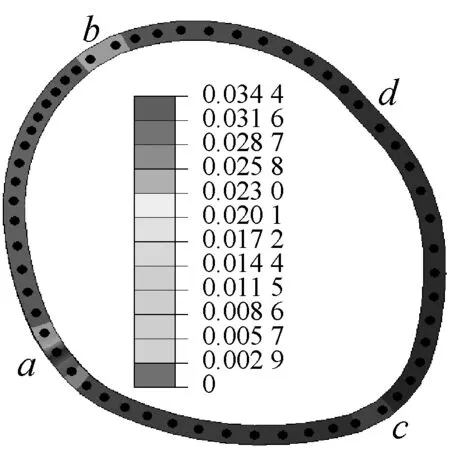
右隧道

左隧道

右隧道
因此进行隧道抗震设计时,一要提高衬砌的整体屈服强度,减小塑性应变;二要在重点塑性区采取相对措施,例如“五心圆形”隧道的圆弧连接处,减少其塑性变形量。
无论弹性还是塑形阶段,右隧道的相对位移均大于左隧道的相对位移,这可能是由于右隧道的上覆土层厚度较薄,周围地基对隧道的约束作用比较小,造成其变形和相对水平位移要比左隧道的大。
绵竹清平波
Mexico波
南京人工波
绵竹清平波

Mexico波

南京人工波
2.2 人防地下室地震反应分析
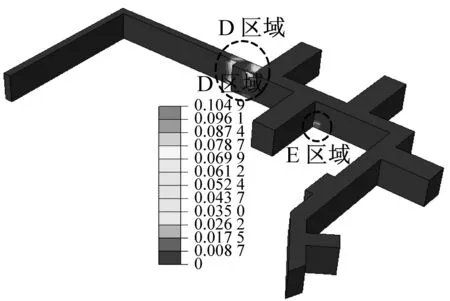
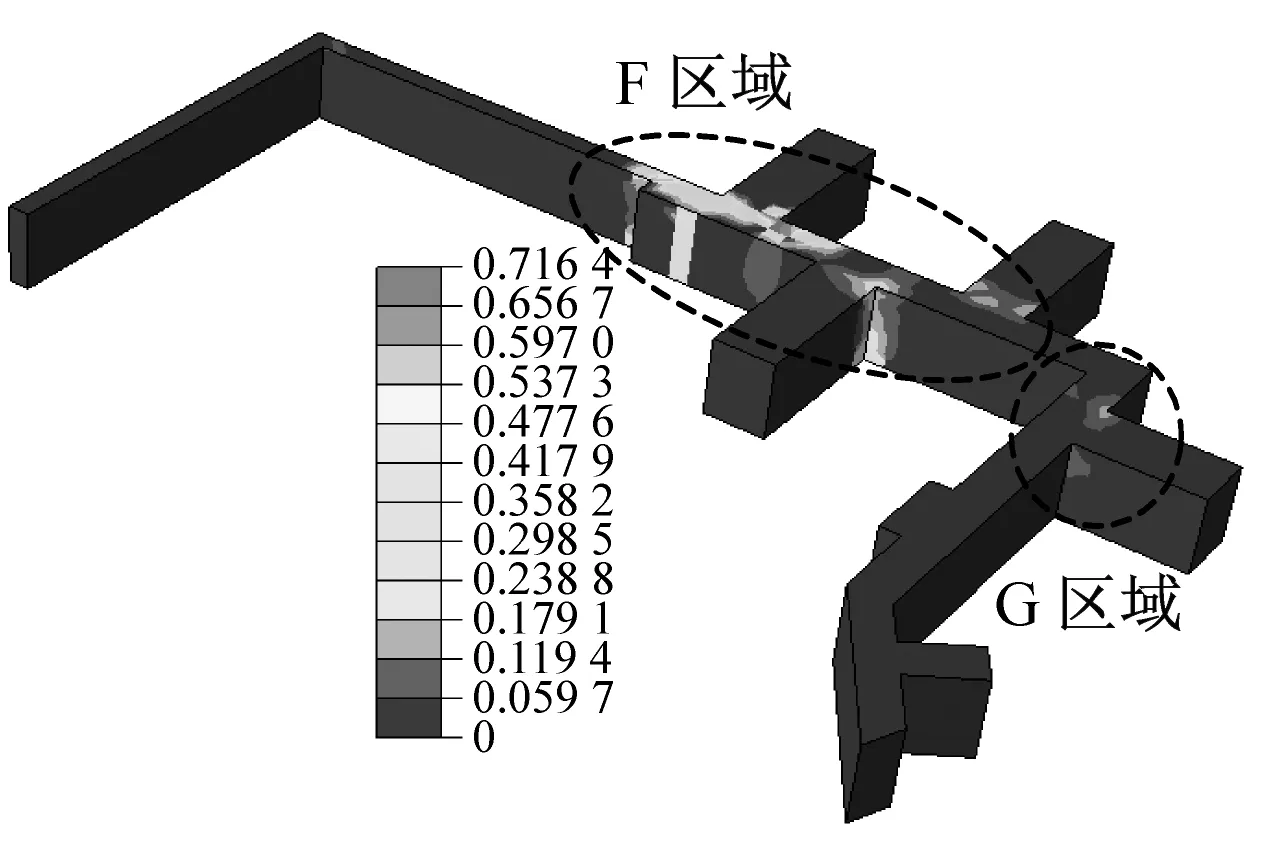
图10为不同地震波作用下人防地下室的损伤图,图中数据为损伤值。
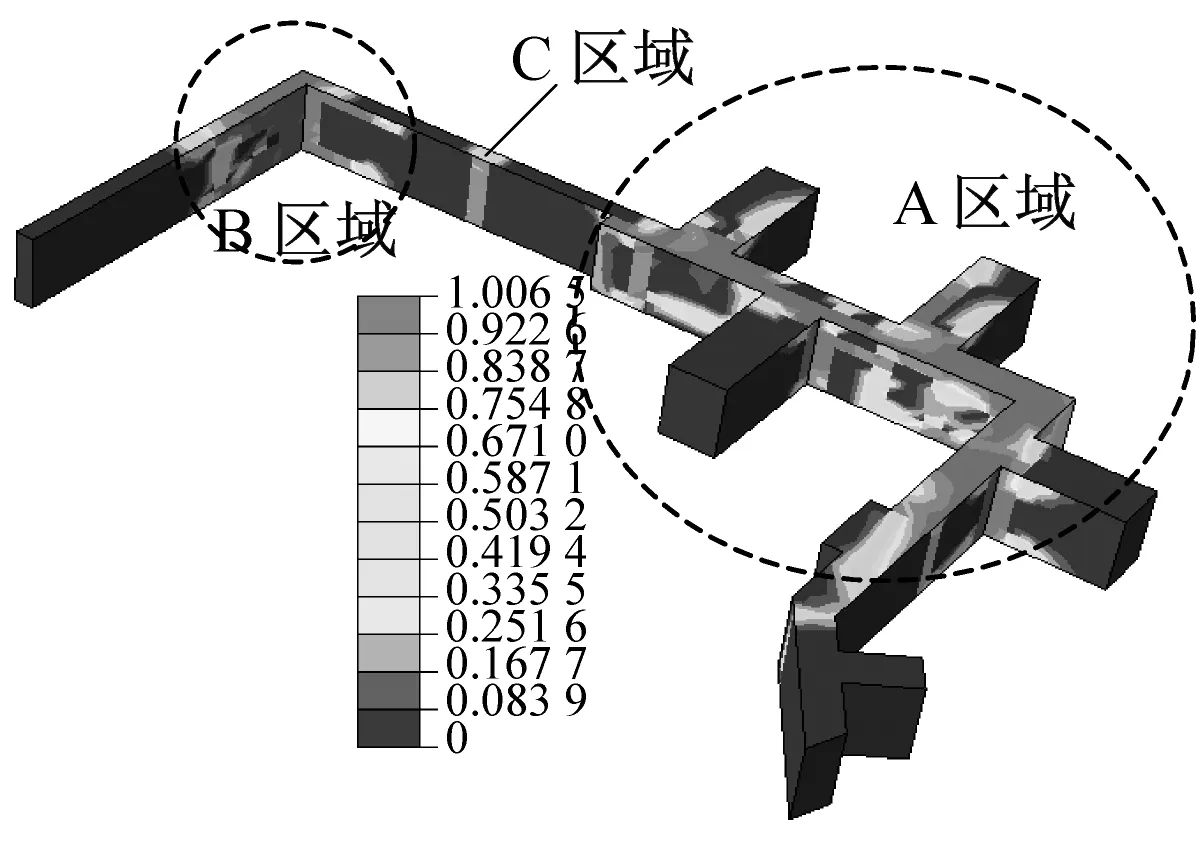
清平波作用下,人防地下室的损伤较为严重,有些部位尤其转角处损伤值大于1,承载力完全丧失。A区域是主要损伤区,原因是此区域有多个转角和通道,应力集中且相互叠加产生大量损伤;B区域仅有1个转角,尽管损伤值大但范围相对较小;图1方向地震波作用下,C区域有较大弯矩导致出现损伤。Mexico波作用下,只有D、E区域墙角处出现小损伤。南京人工波作用下的规律类似,但损伤范围及程度都相对较大,少数部位损伤值达0.716 4,已丧失大部分承载力。
总的来说墙顶底板、侧墙的顶底部,尤其转弯处损伤程度最为严重,应采取相应构造措施,其余部位则较为安全。
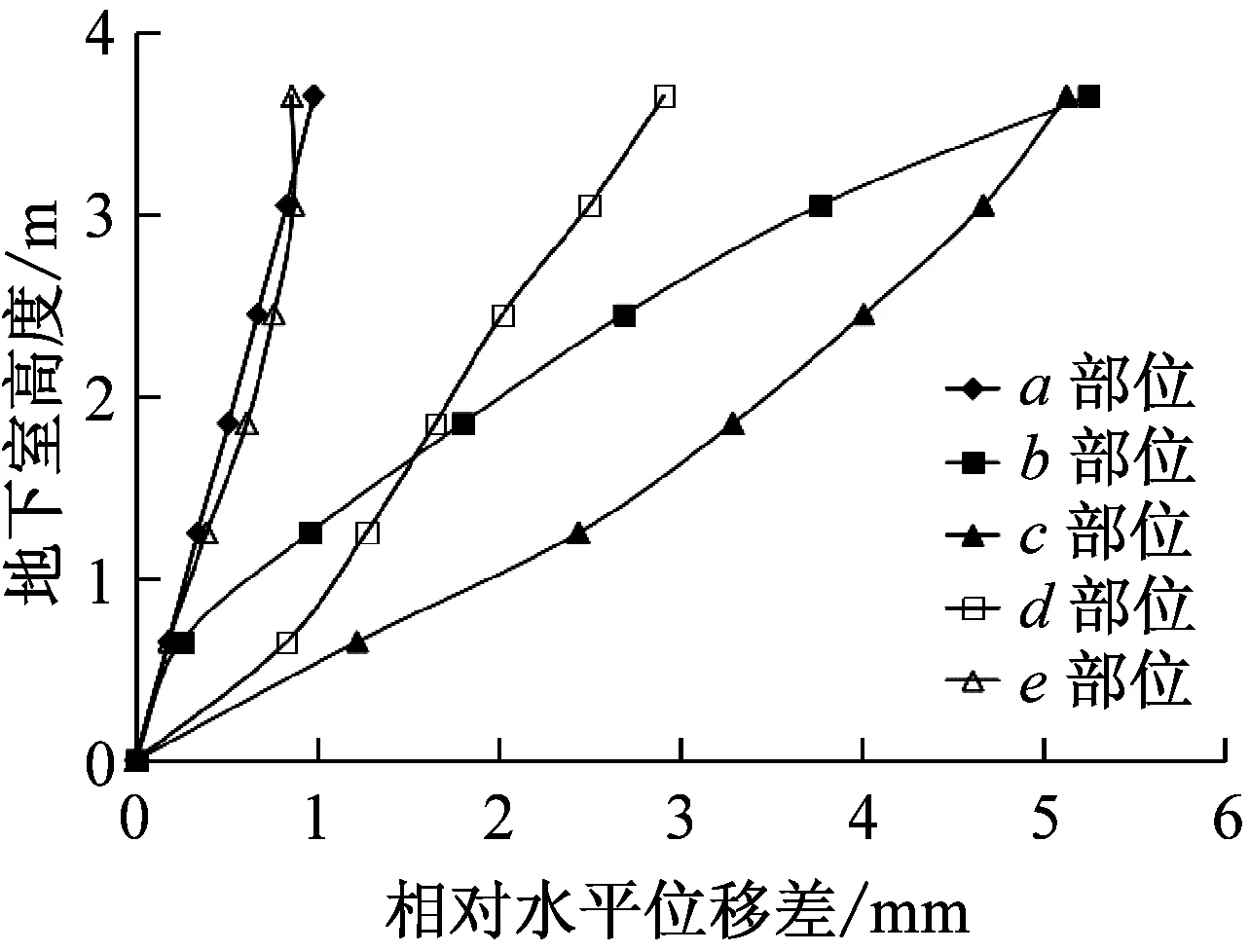
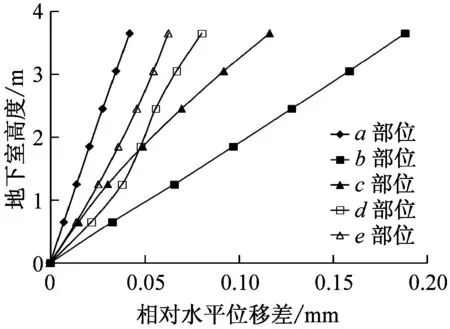
根据损伤云图,图11给出了不同地震波作用下人防地下室5处(见图2)典型部位的相对水平位移沿高度的变化曲线,可以发现:相对位移曲线光滑,沿高度单调增加,未出现隧道相对位移突变的现象。无损伤或小损伤区的相对位移曲线近似成直线,损伤严重区为光滑曲线并且相对位移值也相对较大。中小震作用下相对位移极小,强震清平波作用下最大相对位移也不足6 mm。
绵竹清平波
Mexico波
南京人工波
绵竹清平波
Mexico波
南京人工波
尽管人防地下室有局部区域的损伤值大于隧道损伤值,但是人防地下室的相对位移远小于隧道相对位移,原因是人防地下室混凝土强度高,侧墙厚,且受周围土体约束,不易产生变形;五心圆拱形隧道无顶底板,侧向刚度较小,弧形衬砌较直墙更容易变形。
现代人防地下室集多种功能为一体,使用率高人流量大,应力求形状简单,避免出现过多拐弯,以提高抗震性能。
表3给出了人防地下室的顶底部峰值加速度,同时也给出了隧道的加速度峰值作为对比,可以看出:
近场清平波作用下,人防地下室与隧道的底部峰值加速度均大于顶部峰值加速度,且都小于基岩加速度;而在远场Mexico波作用下则是顶部略大于底部,且都大于于基岩加速度,这种现象是由地震波中高频成分的影响造成的:由于土层对高频地震波有滤波作用,近场地震动高频成分比较丰富,地震波从下卧土层向上传播过程中高频成分被逐步滤掉,因而近场地震动对底部的影响要大于对顶部的影响;由于远场地震动的面波成分高,远场地震动的低频成分在近地表的浅层土体中要比埋深较深土层中更丰富,因而远场地震动对顶部的影响要大于对底部的影响。南京人工波(大震)介于近远场之间的一种“中场”地震动,既有高频的衰减又有低频的放大,规律不明显。

表3 人防地下室、隧道的顶底部峰值加速度
2.3 人防地下室对与隧道的相互反应分析
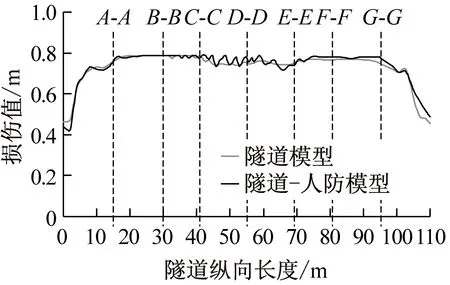
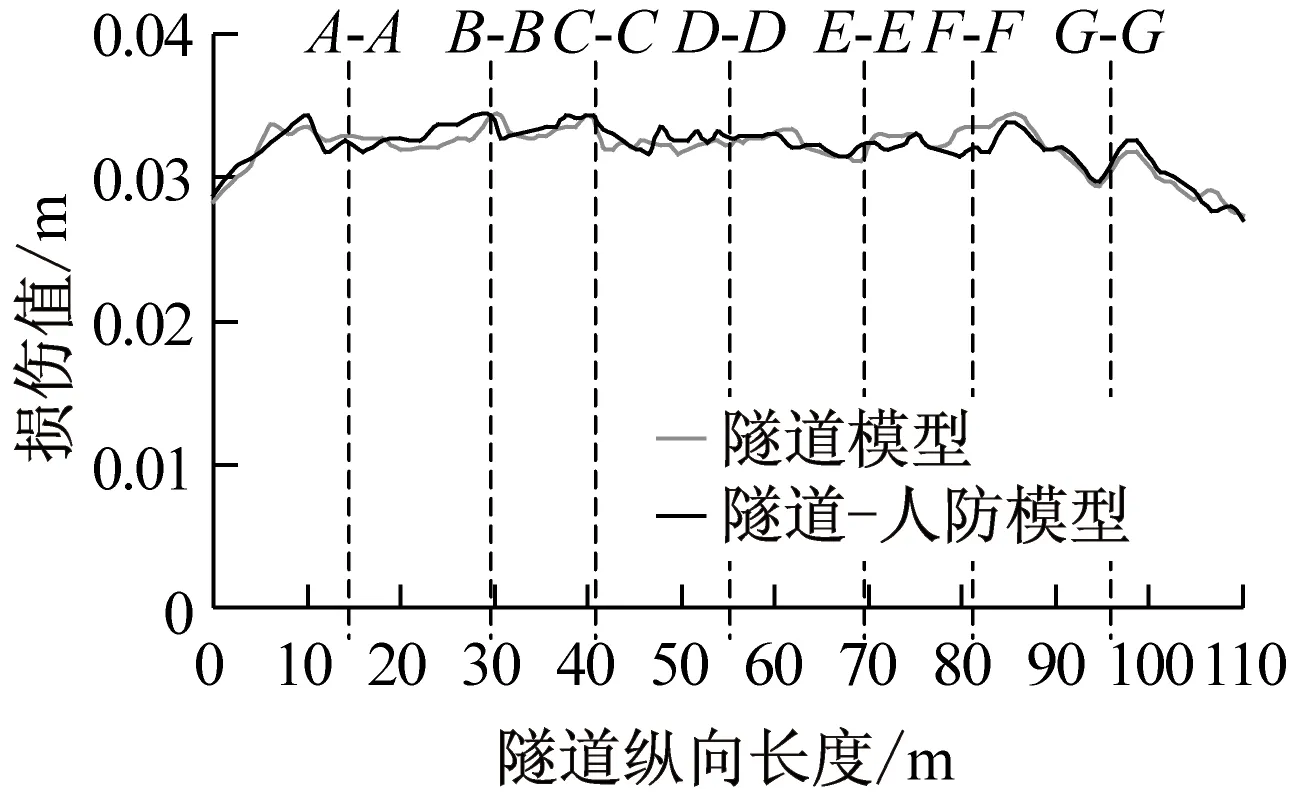
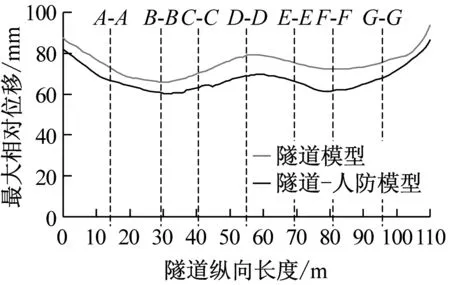
图12和图13分别为不同地震波作用下有无人防地下室时隧道的损伤和相对位移对比图。可以看出有人防地下室时:
(1) 隧道的损伤曲线变化不明显。清平波作用下隧道CE段的损伤增大,曲线也不光滑,CE段外则变化不大。原因是地震波在隧道和人防地下室之间来回反射,加大了隧道衬砌的损伤程度。Mexico波和南京人工波的峰值加速度相对较小,隧道的损伤值无明显变化。
定义与分别为耐用品部门与非耐用品部门的名义工资刚性,其表示任意时期t仅有与比例的工资得到调整。定义与分别表示耐用品部门与非耐用品部门的最优名义工资,与分别为耐用品部门与非耐用品部门就业替代弹性,本文模型经济中两类部门名义工资与均依据Calvo[18]交错方式调整,具体的,与可以分别表示为如下形式:
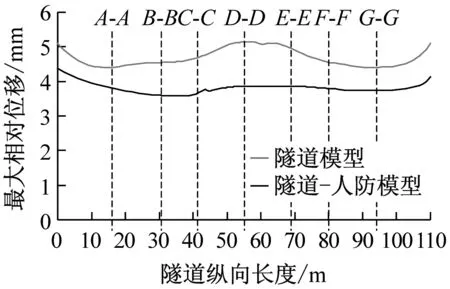
(2) 有人防地下室时,所有地震波作用下的隧道最大相对位移均明显减小,CE段内更显著。因为混凝土刚度远大于土体,不易产生位移和变形,约束了隧道和人防地下室之间土体的位移。
表4为隧道对人防地下室的地震反应分析。可以看出,隧道对人防地下室的损伤和最大相对位移有轻微影响,但规律不明显。可能因为本文的人防地下室形状复杂,地震波方向也不与其任何一条边平行,地震波在传播过程中大量折射反射相互叠加干扰,导致无明显规律。

表4 有无隧道时人防地下室的损伤及最大相对位移对比
绵竹清平波
Mexico波

南京人工波
绵竹清平波
Mexico波

南京人工波
根据城市轨道交通结构抗震设计规范(GB 50909—2014)条文说明5.2.4条以及工程界的一般计算方法,地下结构的允许最大相对位移取地表峰值加速度的15倍,表5根据表3算出了地下结构的允许最大相对位移,并与计算值进行了对比(隧道结构每一个横断面相对位移值不同,这是由于边界条件及有限元计算精度所致,表5取中部D-D断面的值),可以看出:人防地下室的最大相对位移在3种地震波下均远小于极限允许值;而隧道的相对位移值在Mexico波和南京人工波下满足要求,而在清平波下则略大于极限允许值,但旁边有人防地下室时能满足要求。

表5 人防地下室、隧道的最大相对位移值(mm)
综上所述,人防地下室除一些转角处的损伤值略大外,其余部位无论损伤或相对位移均能满足抗震要求,隧道对其影响较小;隧道(非矩形)横断面无棱角,应力集中少,损伤值低,但相对位移值大,尤其在近场大地震作用下可能会超过规范允许值,但人防地下室存在时其相对位移值会变少,因此单纯从抗震角度来说,周边的其他地下结构对于隧道是有利的。
3 结 论
本文以Abaqus软件64CPU显式并行计算集群为平台,以南京地铁4号线鼓楼站的附近的地下建筑构为背景,数值模拟了不同地震波作用下深软地基上的地铁隧道与人防地下室相互作用的三维弹塑性地震反应特性,主要结论如下:
(1) “五心圆形”隧道拱肩及拱腰圆弧连接处的附近损伤值最大,并且会产生塑性位移导致相对位移曲线有突变。
(3) 相比隧道,虽然人防地下室局部区域的损伤值略大,但整体相对位移较小。
(4) 人防地下室会导致隧道的局部损伤值略有增大而相对位移大范围明显减小;隧道对人防地下室的影响无明显规律。
(5) 总的来说人防地下室和隧道的抗震性能都较好,能抵御中小地震,但在近场大地震下隧道的相对位移值偏大。
隧道与地下结构之间的相互作用影响因素太多,包括两者之间平纵接近距离,地震波类型及入射角度,场地土性质、隧道的轮廓形式,其他地下结构的形状以及和隧道的角度等,需进一步研究。

