疏水硅胶颗粒的吸能机理研究
赵 鹏, 余慕春, 陈 前
(1. 南京航空航天大学 机械结构力学及控制国家重点实验室, 南京 210016;2. 中国运载火箭技术研究院, 北京 100076)
冲击问题广泛存在于工程实际中,车辆碰撞、飞机降落、载人卫星返回舱的着陆都伴随着冲击的发生[1-3]。为了确保更高程度的个人和公共保护,对吸能结构的设计和应用提出了越来越多的要求。从20世纪70年代开始,用于耗散碰撞动能吸能材料的研究和开发成为工程领域的热点,已广泛用于车辆防护、工业事故防护和个人防护中。
近年来,研究发现微孔功能材料具有独特的力学特性。根据水进出疏水微孔是否产生迟滞现象,可以将这种液固介质分为无阻尼的分子弹簧[4-7]和有阻尼的疏水硅胶[8-11]。Fadeev等首先通过试验发现,当载荷加载至特定的压力时,水分子开始大量侵入疏水硅胶的纳米微孔中,吸收储存机械能;在卸载阶段,水分子逸出纳米微孔较为困难,在逸出微孔的同时会产生显著的迟滞现象并消耗大量的能量。并且研究了疏水硅胶的硅烷链长度,覆盖密度、硅烷链结构、硅胶孔径等因素对水分子进出疏水微孔压强的影响。Suciu等和Lefevre等分别对疏水颗粒产生迟滞现象的原因进行了阐释。Suciu等认为疏水硅胶产生迟滞是因为微孔液-固界面接触角的滞后;Lefevre等根据能垒计算了水逸出微孔的临界压强和孔径的关系,得出随微孔孔径减小,水逸出疏水微孔的压强显著增加的结论。目前,针对疏水硅胶缓冲介质的研究主要关注其微观工作机理,对于宏观力学建模的研究和缓冲应用还有待于进一步开展。本文将结合微观工作和材料物理特性的统计规律进行宏观力学建模,并进一步分析材料的吸能特性和缓冲效率。
将疏水硅胶缓冲介质封存于如图1所示的活塞液压缸结构中,即可形成疏水硅胶缓冲器。冲击发生时,水分子进出硅胶颗粒的疏水微孔,从而实现能量的消耗。本文基于理论分析和试验测试,建立了并验证疏水硅胶颗粒的宏观力学模型。首先,基于Laplace-Washburn方程和接触角迟滞模型,揭示水进出疏水微孔产生迟滞现象的机理,建立疏水硅胶力学性能的理论计算模型;随后,以C-18疏水硅胶与水的混合物为工作介质,开展试验测试其准静态特性,通过对比试验测试结果和理论分析结果验证本文理论方法的准确性。最后,本文分析冲击载荷作用下疏水硅胶缓冲器的耗能特性。本文研究内容将为疏水硅胶缓冲介质的工程应用奠定良好的基础。
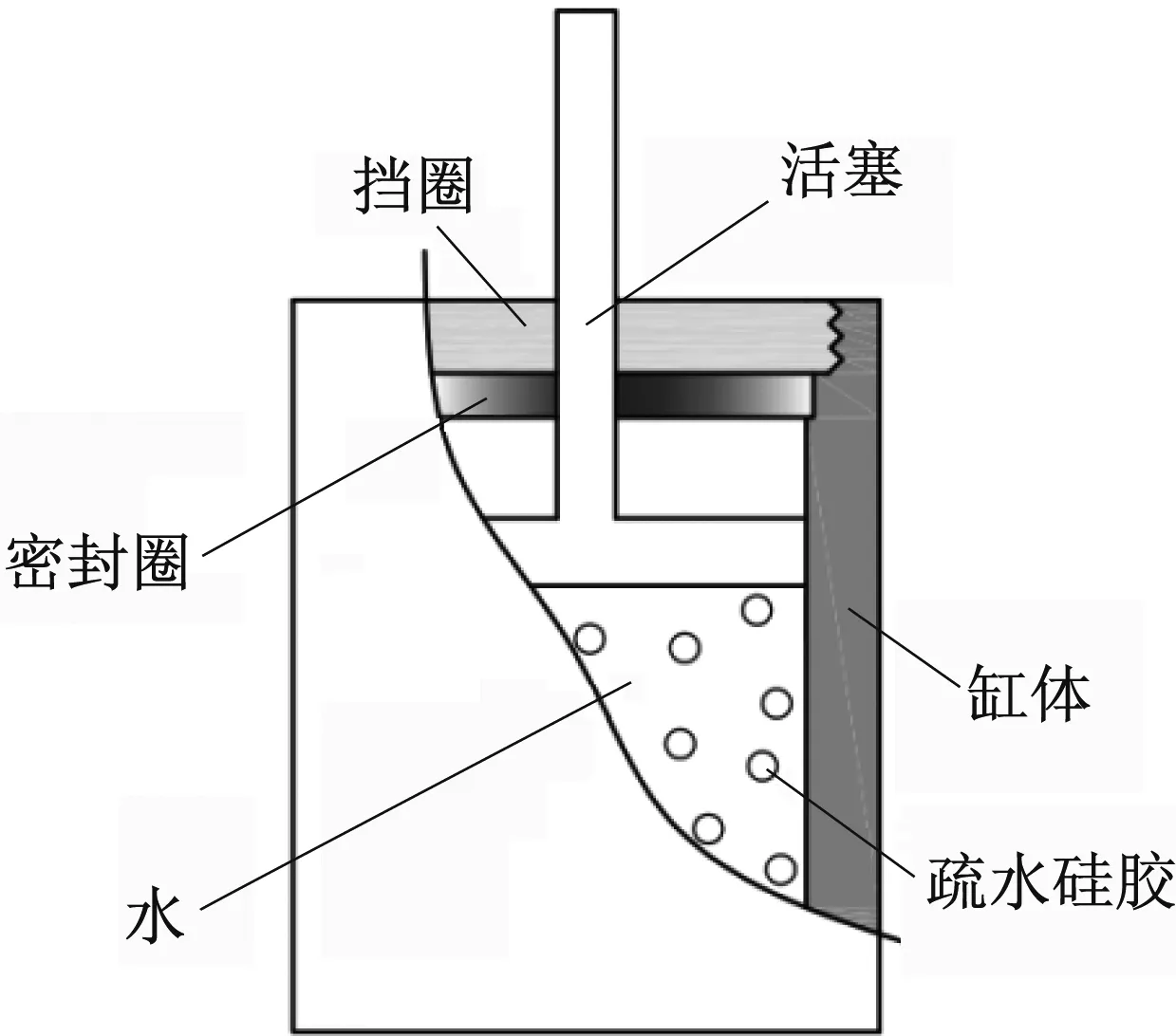
图1 疏水硅胶缓冲器示意图
1 力学模型建立
目前,对于疏水硅胶特性研究主要集中于试验测试,较少涉及疏水硅胶的力学行为的力学模型。本节以疏水微孔内的液柱的微观力学行为基础,建立水进入和逸出单条疏水微孔的微观力学模型,并结合材料物理特性的统计规律,实现疏水硅胶的宏观力学建模。
1.1 疏水微孔液柱微观力学行为
对于疏水微孔液固接触界面,其接触角θ大于90°。水进入单条微孔时的受力情况如图2所示。其中Pc是附加毛细力,Pair是孔内气体压强,P是外部液体压强。微孔内水受力平衡如式(1)所示
P=Pc+Pair
(1)
毛细孔内液固界面接触的Laplace-Washburn方程为
Pc=-2σLcosθ/r+Pair
(2)
式中:σL为液体表面张力,r为微孔半径,θ为接触角。
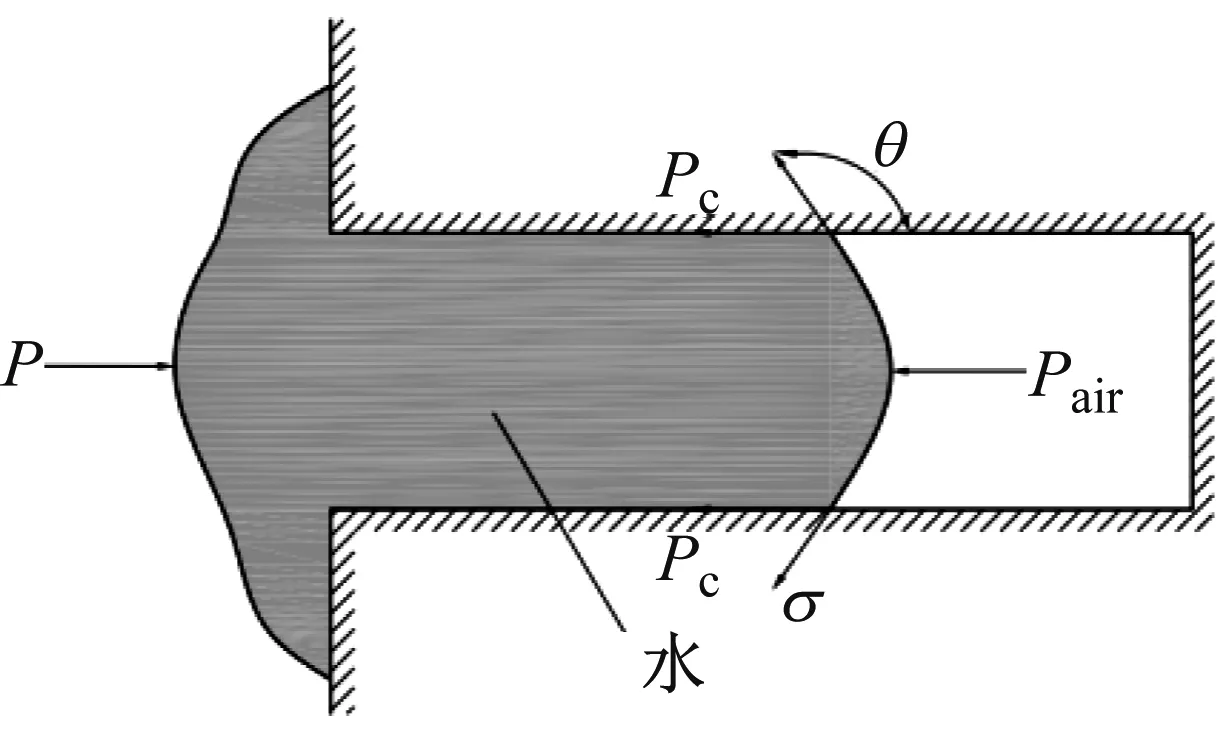
图2 水侵入单条疏水微孔受力图
对于纳米级高疏水性微孔,可忽略Pair[12]。在此基础上可以得到水侵入单条疏水微孔所需的外部压强P为
P=Pc=-2σLcosθ/r
(3)
由式(3)可知:可以通过微孔的物理参数计算水进入微孔所需的压强P,而不考虑整个入水的过程,因此能够较为方便准确的计算出这一特定外加压强。
水逸出疏水微孔的过程可以看作是侵入微孔的逆过程,同样遵循Laplace-Washburn方程,但在卸载阶段,疏水硅胶的体积变化量比加载阶段要小,即产生了迟滞现象。文献[13]表明,正是由于水进入和逸出疏水微孔的接触角存在差异,才导致加载卸载过程存在迟滞现象。接触角迟滞产生的原因为液-固接触界面粗糙引起的[14-16],液-固接触界面的粗糙包括物理粗糙(接触界面不光滑)和化学粗糙(接触界面化学性质不均匀)引起的。纳米尺度下水侵入和逸出疏水微孔的迟滞现象如图3所示。当水侵入单条疏水微孔时,其接触角为θa;水逸出同一微孔时,其接触角变为θr,并且有θa>θr。由式(3)可知,当水进出微孔的接触角不同时,入水压强要大于出水压强,即在加载卸载过程产生迟滞现象。

图3 接触角迟滞模型
1.2 疏水硅胶宏观力学建模
当压缩疏水硅胶缓冲器时,水分子开始侵入大量疏水微孔,由于这些微孔的孔径及疏水性不尽相同,因此需要结合材料物理特性的统计规律进行宏观力学建模。疏水硅胶在加载阶段体积变化量与外加压强之间的关系分为三个阶段:第一阶段和第三阶段斜率相同,第一阶段,外压力不足以迫使水分子进入硅胶颗粒的疏水微孔,随着压力的增加,液体的可压缩性使得疏水硅胶体积减小;与第一阶段不同的是,在第三阶段,微孔已经完全达到饱和,水分子无法进入微孔,同样是液体的可压缩性使得疏水硅胶体积持续减小;第二阶段,外界压强达到水分子进入微孔的临界压强,开始迫使水分子大量进入硅胶颗粒的疏水微孔,此后,较小的压力增加将引起疏水硅胶的体积大幅度减小。因此在水侵入大量疏水微孔的过程中,可以观察到明显的分段特性。
设外加压强为P,疏水硅胶的总体积变化量V(P);疏水硅胶孔径最大值为rmax,孔径最小值为rmin;入水阶段,疏水硅胶颗粒接触角最大值为θmax,最小值为θmin;疏水硅胶质量为m;单位质量疏水硅胶颗粒有效孔容积为Vp;水的体积为Vw;K(P)为水的压缩率;V(r)为有效孔容积相对于孔径的概率密度函数,f1(θ)为接触角的概率密度函数。则有:
K(P)=4.5×10-4(P×10-6-0.1)
(4)
(5)
(6)
其中:
(7)
(8)
由式(6)和(7)可知,f(θ)是高斯分布的概率密度函数;F(θ)是高斯分布的概率分布函数。
第一阶段和第三阶段疏水硅胶的体积变化量可以通过水的压缩率来计算,当外加压强从峰值开始逐渐增大时,由于液体的可压缩性,疏水硅胶的体积变化量为
V(P)=VwK(P)
(9)
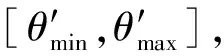
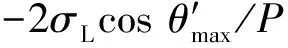
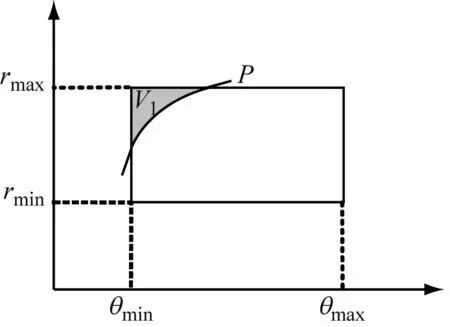
(a) 入水第一阶段
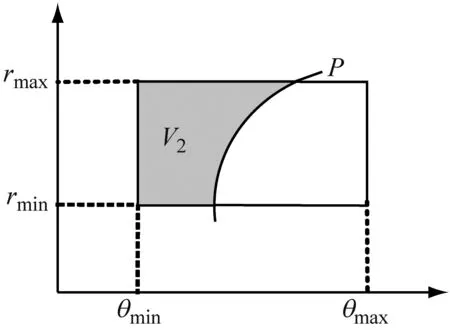
(b) 入水第二阶段
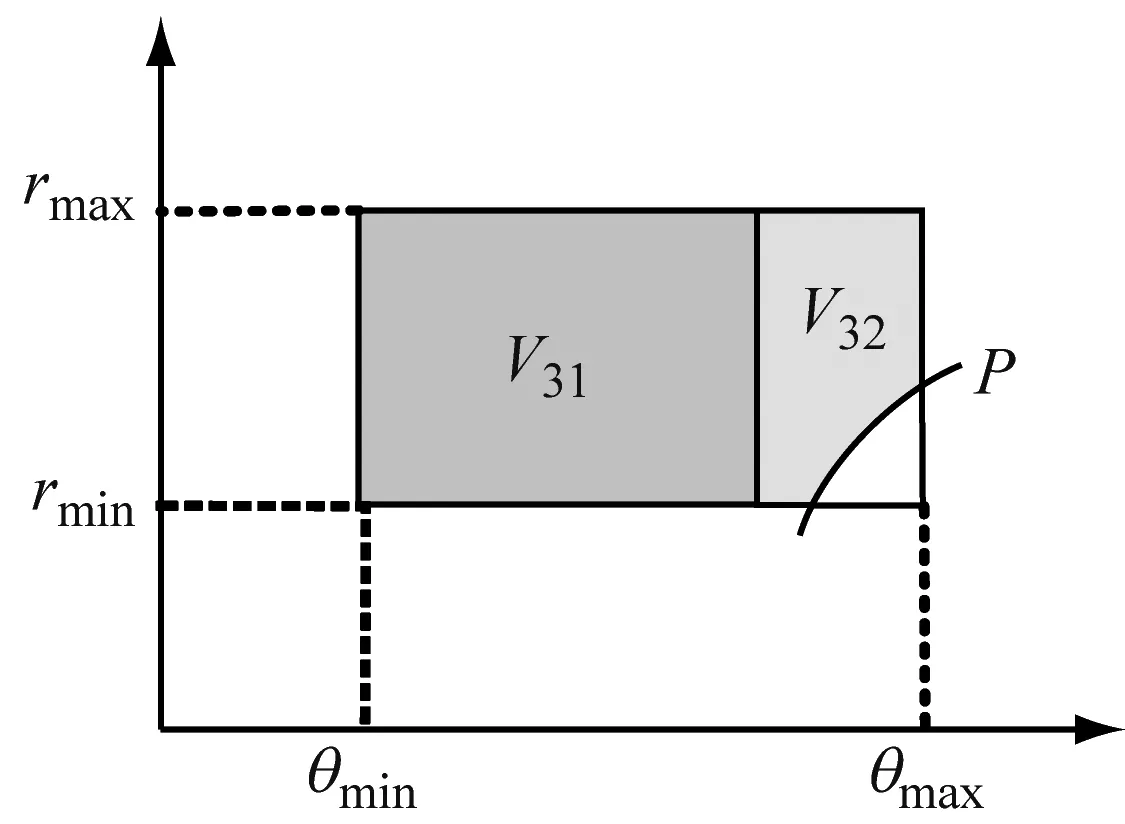
(c) 入水第三阶段
结合图4,逸出微孔水的体积为
V1(P)=VwK(P)+
(10)
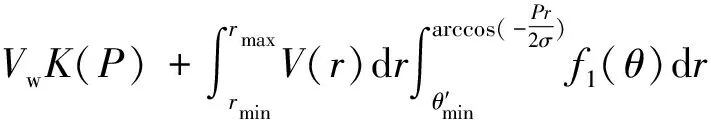
(11)
V3(P)=V31(P)+V32(P)
(12)
其中:
(13)
(14)
当外加压强逐渐增加到临界压强时,水已经完全侵入疏水微孔,由于液体的可压缩性,疏水硅胶的体积的变化量为
V(P)=VwK(P)+mVp
(15)
综合式(9)~式(15),以Laplace-Washburn方程为基础,结合接触角迟滞模型,可以得到疏水硅胶在加载阶段体积变化量与外加压强之间的关系。其中,式(9)和式(15)分别表示纯水压缩过程中的体积改变量,式(10)~式(14)表示第二阶段水分子侵入疏水微孔过程的体积改变量。
水逸出疏水微孔的过程是进入疏水过程的逆过程,由于接触角迟滞,水逸出疏水微孔的临界压强远低于水进入疏水微孔的临界压强。从而使得在相同的压强下,卸载阶段疏水硅胶的体积变化量比加载阶段要小。基于上述假设,认为水逸出大量微孔时的接触角分布和侵入微孔时一致,同样服从正态分布θ~N(μ,η2),只是卸载阶段疏水孔道的接触角分布值小于加载阶段的接触角。这一假设采用统计的方法,综合考虑硅胶微孔表面粗糙度和化学性质差异性,得到的结果更符合实际情况。水逸出疏水微孔的过程与侵入微孔的过程类似,在这里就不在赘述。
将表1中的仿真参数代入式(9)~式(15)中,其中,室温下水的表面张力为0.072 8 Pa,正态分布参数根据材料自身规律确定,其余材料参数由材料生产厂家提供。采用数值积分的方法,处理并化简后可得疏水硅胶在加载-卸载阶段体积变化量和外加压强的关系如图5所示。由图5可知,在15 MPa水分子开始进入疏水微孔,47 MPa饱和,2 MPa逸出,-5 MPa排净。实际应用中,由于液压缸体内无法产生负压强,会有部分水分子滞留在疏水微孔中,无法逸出。

表1 仿真参数
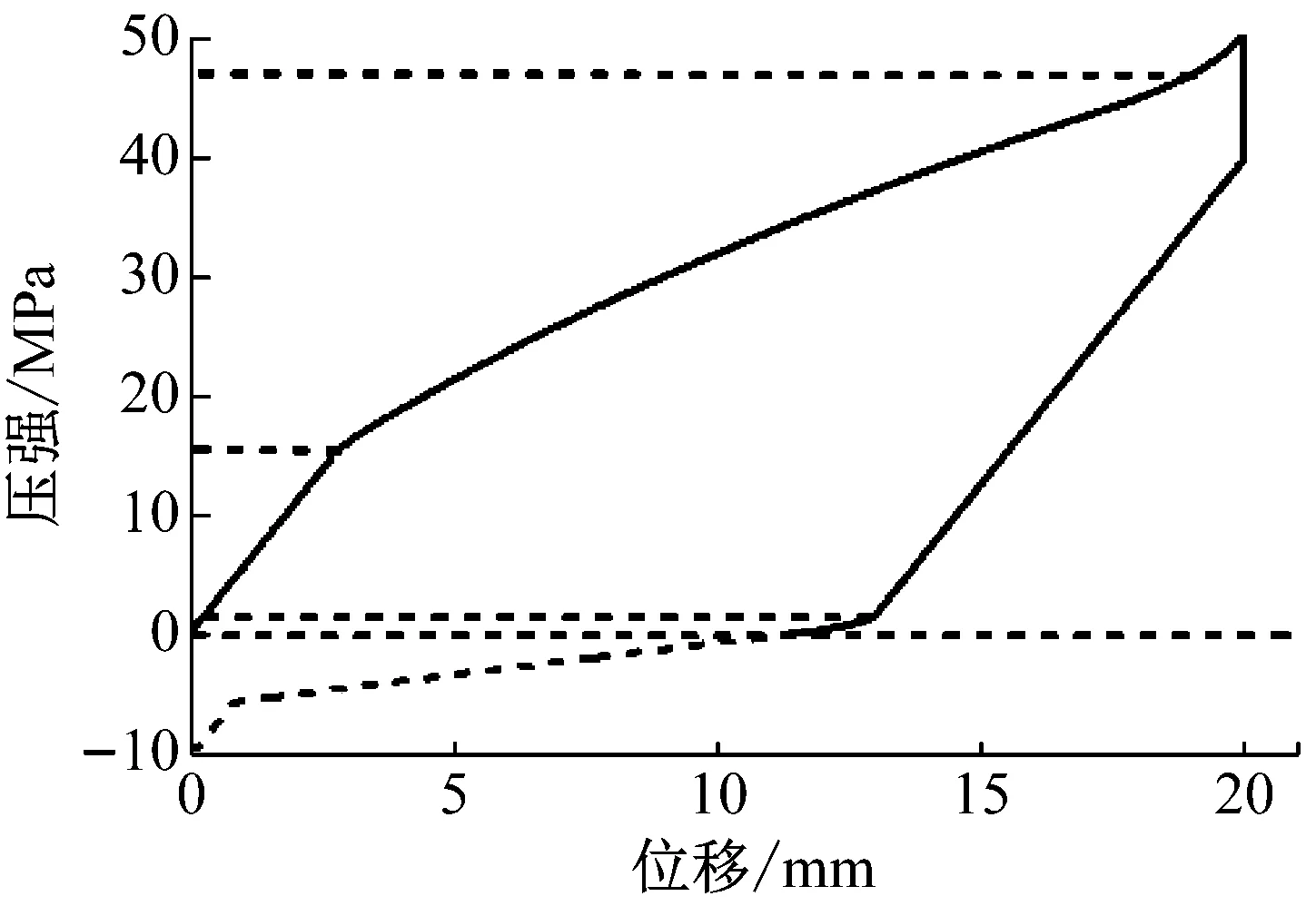
图5 疏水硅胶理论结果
2 试验验证
为验证本文疏水硅胶理论模型的准确性,本文设计一种疏水硅胶缓冲器,并通过疲劳试验机对疏水硅胶缓冲器进行加载—卸载,得到准静态条件下,缓冲器的力-位移曲线。试验装置如图6所示,将一定量的水和C-18疏水硅胶组成的混合介质置于密封的活塞液压缸中,形成疏水硅胶缓冲器;图7为该装置所用的C-18疏水硅胶。其中C-18疏水硅胶的平均粒径和孔径分别为50 nm和6 nm,液压缸活塞直径和缸体体积分别为10 mm和30 mL。
图8给出了疏水硅胶的准静态实验结果。从图8可以看出,在加载阶段,疏水硅胶表现出明显的分段刚度特性。第一阶段和第三阶段的斜率几乎相同,说明这两个阶段的主要过程为水的压缩过程,没有水分子进入疏水微孔。第二阶段斜率降低是由于在该阶段,水分子开始大量侵入疏水微孔;卸载阶段是加载阶段的逆过程,但在卸载阶段,疏水硅胶的体积变化量要远远小于加载阶段,侵入微孔的水并没有完全逸出疏水微孔,产生较大的迟滞现象。利用接触角迟滞理论可以解释迟滞现象产生的原因。当入水接触角与出水接触角相差较大时,虽然入水时的接触角大于90°,但出水时的接触角有可能接近90°,甚至小于90°。因此,在卸载过程中,对于一些接触角小于90°的微孔,水将滞留在微孔中。只有接触角大于90°的疏水微孔中的水能够逸出微孔。此外,由于疏水微孔表面的某些缺陷,也会使得部分水分子被滞留在微孔中,从而导致迟滞现象的发生。在开始卸载过程中力信号出现一定程度的衰减,该现象出现的原因可能是由于试验机存在一定的机械间隙,导致在卸载阶段,施加的作用力未能补偿该间隙。

图6 试验装置

图7 疏水硅胶颗粒
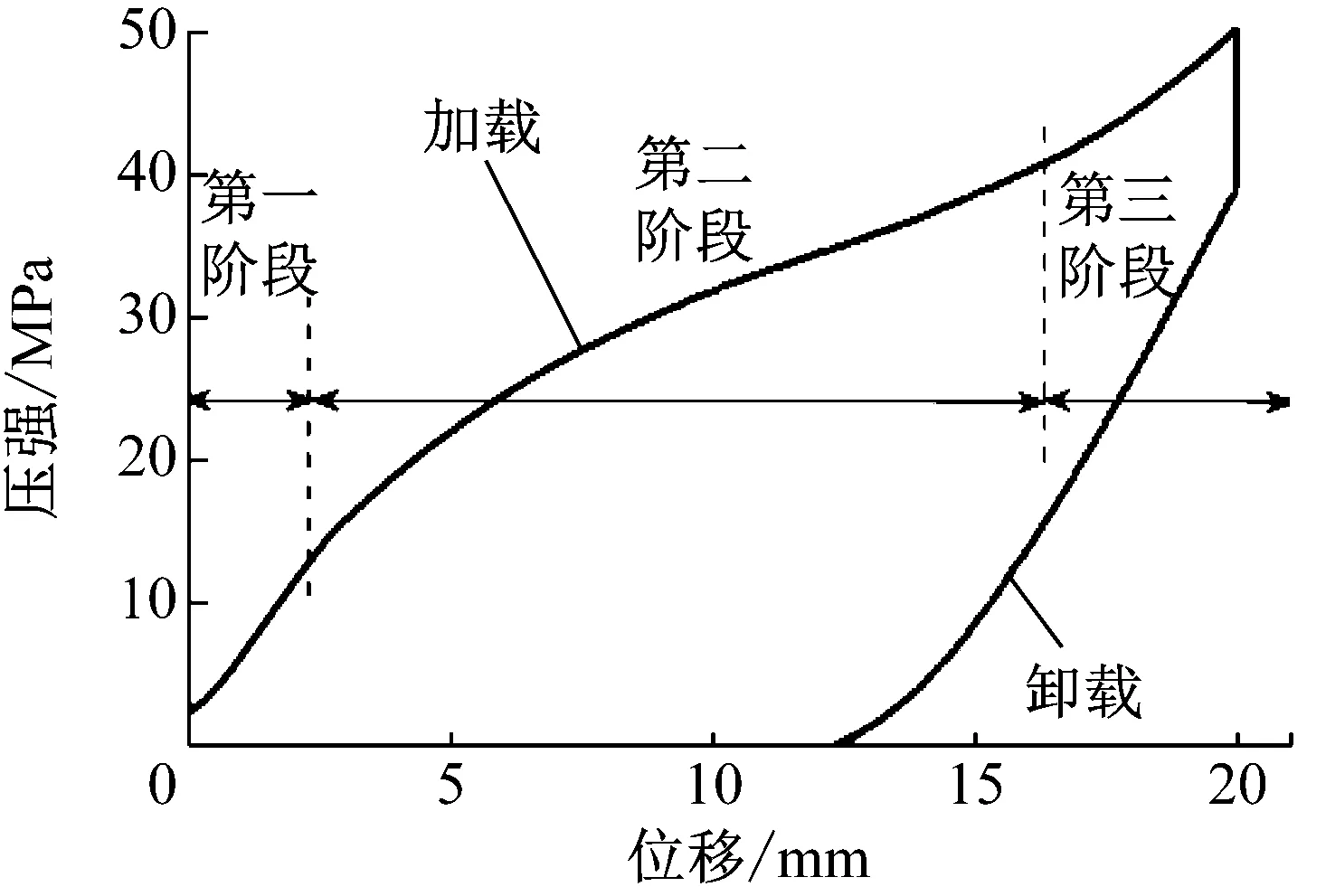
图8 准静态试验结果
为了进一步验证上述理论,图9给出了在多次循环载荷下,疏水硅胶的加载-卸载曲线。从图9中可以看出,疏水硅胶的迟滞环面积随着循环次数的增加而减小。在第一次循环时,可以看到明显的迟滞现象,此时耗能效果最为显著。随着循环次数的递增,耗能效果会逐步减弱。后三次循环的迟滞效果虽然十分接近,但与第一次相比,仍然有较大差距。进一步说明由于接触角的差异,导致部分水分子无法逸出微孔,从而削减了疏水硅胶后续耗能效果。

图9 多次循环载荷下的迟滞效应
图10是将理论结果和第一次循环载荷下的试验结果相比较。由图可知,在加载阶段,二者吻合的较好。在卸载阶段,部分理论计算结果和试验结果出现了一定的偏差,这是因为在加载阶段,水分子侵入疏水微孔,导致缸体内纯水体积减少,使得在卸载阶段,纯水的体积变化量较理论值有一定偏差。值得说明的是,在卸载阶段,由于力信号出现衰减和部分微孔接触角变小,使得当缸体内压强达到零时,仍有部分水分子滞留在微孔中。如图10所示,利用理论模型可以计算出外部压强小于零时水逸出疏水硅胶的过程,验证了疏水硅胶的工作机理。

图10 第一次循环载荷时试验结果与理论结果比较
为了进一步验证理论结果的正确性,将理论结果和第二次循环载荷下的试验结果相比较。由于部分水分子滞留在疏水微孔中,在第一次循环载荷结束后,认为单位质量疏水硅胶颗粒有效孔容积将有所减小,其余物理量保持不变。试验表明:单位质量疏水硅胶有效孔容积由原来的1.70-7m3降为4.58×10-8m3,将改变后的有效孔容积和表1中的其他参数代入式(9)式(15)中,可得疏水硅胶在第二次循环载荷下,体积变化量和外加压强的关系,理论与试验对比结果如图11所示,由图11可知,理论计算结果和试验结果吻合较好,同时也说明了当部分水分子滞留微孔时,仅会改变疏水硅胶的有效孔容积,并不会对其他物理量产生影响。
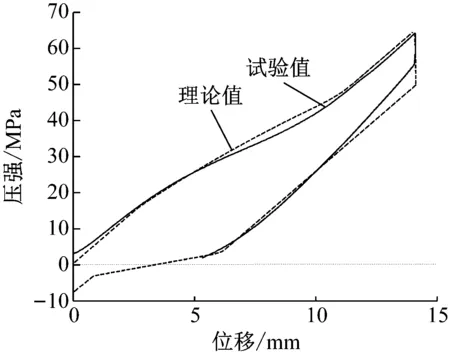
图11 第二次循环载荷时试验结果与理论结果比较
3 耗能特性分析
本节中对疏水硅胶缓冲器的耗能特性进行分析。一个理想缓冲器应该在降低最大冲击力峰值的同时吸收更多的能量。因此,在冲击发生时,缓冲器受到的作用力会急剧增加,并且会在该峰值保持一段时间。冲击结束后,缓冲器受到的作用力急剧下降,发生迟滞现象,从而吸收消耗能量。
图12是疏水硅胶缓冲器第一次循环时的加载—卸载曲线。在图12中,曲线A-B-C-D和曲线D-E-F分别为加载曲线和卸载曲线。加载曲线A-B-C-D和卸载曲线D-E-F所围成的面积代表疏水硅胶消耗的能量Ed,加载曲线A-B-C-D与x轴所围成的面积代表一个循环载荷下,疏水硅胶吸收的总能量Ea。缓冲器的缓冲效率(表征消耗能量的能力)η定义为
(16)
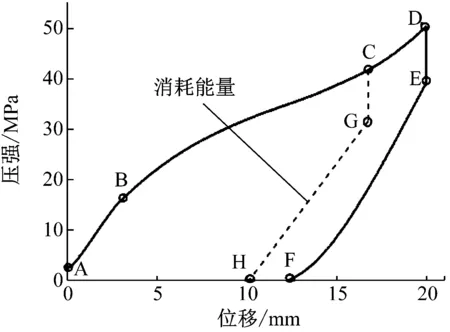
图12 疏水硅胶耗能特性
利用图12的实测数据可以计算出疏水硅胶缓冲器在一个循环载荷下的缓冲效率为79.3%。相比之下,液压缓冲器的缓冲效率通常低于50%,而在实际应用中,其效率往往只能达到30%~40%。计算结果表明疏水硅胶缓冲器具有优异的耗能特性。
为了降低缓冲过程中最大冲击力幅值,疏水硅胶缓冲器的最大位移值应限制在疏水硅胶的入水阶段,一旦缓冲器位移进入第三阶段,冲击力幅值会大幅度增加。换言之,最大位移应限制在B-C之间,如图12所示。加载-卸载曲线应为A-B-C-G-H,此时非常接近理想缓冲器的迟滞曲线。在该情况下,冲击力幅值将得到有效抑制。此时,计算得到疏水硅胶耗散的能量为327.53 J。考虑到缓冲器中填充5 g硅胶颗粒,因此每克硅胶颗粒能够吸收65.5 J的机械能。此外,可以通过改变填充疏水硅胶的质量从而改变疏水硅胶缓冲器的缓冲特性,以满足不同的缓冲要求。
除了具有良好的耗能特性,疏水硅胶缓冲器还具有诸多优点:疏水硅胶缓冲器与液压式缓冲器不同,液压式缓冲器通过热能耗散的方式消耗机械能,而疏水硅胶缓冲器则是利用水进出疏水微孔,通过产生更多的液固界面,将机械能转化为液-固表面的界面能。因此,疏水硅胶缓冲器在缓冲过程中产生的热量十分有限。此外,疏水硅胶是将烷基氯硅烷嫁接到传统硅胶颗粒而形成的有机物。由于烷基氯硅烷链长的不同,可以合成出具有不同孔道结构和拓扑形状的疏水硅胶颗粒,从而满足不同的缓冲要求。
4 结 论
本文发现了一种新型缓冲材料——疏水硅胶颗粒,从Laplace-Washburn方程和接触角迟滞模型出发,讨论了疏水硅胶颗粒产生迟滞现象的原因,并建立了理论计算模型,该模型的仿真结果与准静态试验结果有吻合较好;本文对疏水硅胶力学性能进行了理论研究和试验,发现在初次载荷下,疏水硅胶颗粒具有优异的吸能效果;在后续载荷中,耗能特性虽有所下降,但仍有持续的耗能效果,特别适合于航天器回收、飞机起落架、车辆悬架防护等领域。本文主要结论归纳如下:
(1) 准静态条件下的试验结果和理论结果具有较好的一致性,这表明了本文理论方法的合理性和有效性。
(2) 在多次循环载荷下,疏水硅胶的迟滞效应会随着循环次数的增加而减小,导致在后续的缓冲过程中,疏水硅胶的耗能效率有一定程度的减少。
(3) 疏水硅胶具有优异的缓冲特性,在第一次循环载荷下,其缓冲效率为79.3%,远远优于液压缓冲器的缓冲性能。

