基于复合耗能假设的黏弹夹芯梁振动的有限元分析
黄志诚, 刘莉娅, 吴南星, 王兴国, 褚福磊
(1. 景德镇陶瓷大学 机电学院, 江西 景德镇 333000; 2. 清华大学 机械工程系, 北京 100084)
黏弹性夹芯复合材料又称黏弹夹芯结构,它是在两弹性层之间夹有黏弹性芯层,以减小结构的振动振幅和噪声。它们广泛用于航天、航空、航海和汽车工业中[1]。典型的黏弹夹芯梁结构如图1所示。从图1可以看出,在黏弹夹芯梁结构中,一个轻质的黏弹性材料层黏结在两个分别称之为基梁层和约束层的弹性表面层之间。当基梁产生振动时,其振动能量通过中间黏弹性层的变形转化为热能耗散,达到减振降噪的目的。

图1 黏弹夹芯梁结构
众多学者对黏弹夹芯梁的建模进行了研究。这些模型的理论基础主要分为两类:剪切耗能假设和压缩耗能假设。前者认为黏弹夹芯梁的振动能量是通过中间黏性层的纵向剪切变形耗散的,这类模型因其物理原理明确,建模相对简单,应用较多。如早期的Kerwin[2], DiTaranto等[3], Mead等[4], Yan等[5],及Rao等[6]基于剪切耗能假设建立了黏弹夹芯梁的解析模型并应用至今。另外众多学者基于剪切耗能假设建立了黏弹夹芯梁的有限元模型[7-13]。在另一方面,也有一些学者发现了黏弹夹芯结构的压缩阻尼。在20世纪七八十年代,Douglas等[14-15]通过对黏弹夹芯梁的实验证明了其中压缩阻尼的存在。并基于压缩耗能假设建立了黏弹夹芯梁的解析模型,忽略了黏弹性层的剪切变形。他们认为在以黏弹性层的压缩共振频率为中心的一个狭窄频段内,压缩阻尼是主要的阻尼形式。但他们的工作在当时并没有引起人们的重视。Sisemore等[16-17]对悬臂黏弹夹芯梁结构进行了较深入的研究,不仅从实验上证明了压缩阻尼的存在,还基于压缩耗能假设建立了黏弹夹芯梁梁结构的解析模型。也有极少数学者[18-19]对黏弹夹芯结构建立了同时考虑剪切和压缩的复合解析模型。但结果表明这些复合阻尼模型在很宽的频带内会高估系统的损耗因子。
从文献检索的结果来看,目前黏弹夹芯梁的建模主要是基于剪切耗能假设,压缩耗能也逐渐引起人们兴趣,但从作者前期研究结果来看,剪切模型适用于黏弹夹芯梁各层较薄的情况[20],而压缩模型对阻尼的预估存在不足[21]。事实上,当黏弹夹芯结构发生振动时,黏弹性层中剪切和压缩两种阻尼均存在,在某些情况下,仅考虑一种模式会引起较大误差。针对这些不足,本文提出了一种黏弹夹芯梁的复合有限元模型。该模型基于复合耗能假设,同时考虑了黏弹性层的剪切耗能和压缩耗能,然后应用该模型对不同边界条件和几何参数黏弹夹芯梁进行振动分析,通过与实验及其它常用模型的计算结果对比来验证该模型,所得结果有益于工程上黏弹夹芯梁结构动力学参数预估,所以本文工作有一定的工程参考价值。
1 黏弹夹芯梁有限元建模
1.1 基本假设
① 基梁和约束层可看作Euler-Bernoulli梁;② 基梁和约束层有不同的横向位移(挠度);③ 黏弹性层的横向位移是基梁和约束层横向位移的线性插入值;④ 复合结构阻尼由黏弹性层的剪切和压缩变形引起;⑤ 各层完美黏结,无相对滑动。
1.2 几何和变形关系
在上述假设下,黏弹夹芯梁的变形关系如图2所示。
图2中主要几何参数意义如下:L为梁长度;hc,hv和hb分别为约束层、黏弹性层和基梁的厚度;wc和wb分别为约束层和基梁的横向位移;∂wc/∂x和∂wb/∂x分别为约束层和基梁的转角;φ和β分别为黏弹性层的转角和剪应变。

图2 复合耗能假设下EVEC梁的变形和几何关系
根据假设,约束层和基梁被视为Euler-Bernoulli梁,忽略其剪切变形,则其内部任一点的纵向位移u(i)和横向位移w(i)为[22]
(1)
式中:ui(x,t)和wi(x,t)分别为第i层中面的纵向和横向位移。zi为该点到第i层中面的距离。它们在局部坐标系中的位置关系,如图3所示。

图3 黏弹夹芯梁各层的局部坐标系
从图3可知,对于约束层下表面上的点,其z坐标为zc=-hc/2;对于基梁上表面的点而言,其z坐标为zb=hb/2。将它们分别代入式(1)可得黏弹性层的上、下表面的轴向(x向)位移表达式分别为
(2a)
(2b)
根据假设,黏弹性层的中面纵向位移为
(3)
由于黏弹性层相对于两个弹性表面层而言非常软,其横向位移可假定为是约束层和基梁的线性函数,即定义黏弹性层的横向位移为约束层和基梁的横向位移的平均值为
(4)
根据假设及图2所示几何关系,黏弹性层的剪应变为
(5)
显然黏弹性层的压应变为
(6)
1.3 自由度和形函数
构造如图4所示黏弹夹芯梁单元。这是一种2节

图4 黏弹夹芯梁单元节点位移示意图
点12自由度复合梁单元。每个节点的6个自由度分别为约束层和基梁的纵向位移,横向位移和转角。
单元内任一点的位移向量写成矩阵的形式可以表示为
(7)
式中各位移分量分别为:约束层和基梁的轴向位移uc,ub,横向位移wc,wb和转角θc,θb,它们可以通过以下函数插值得到
wc=a1+a2x+a3x2+a4x3,
wb=a7+a8x+a9x2+a10x3,
(8)
式中,常数项 {a1,a2,…,a12}由单元两个节点的12个位移分量决定。
节点的位移向量为
(9)
则同理单元内任一点的各位移向量可以由形函数插值得到:
wc=N1Δe
(10a)
θc=N2Δe
(10b)
uc=N3Δe
(10c)
wb=N4Δe
(10d)
θb=N5Δe
(10e)
ub=N6Δe
(10f)
式中各形函数表达式为
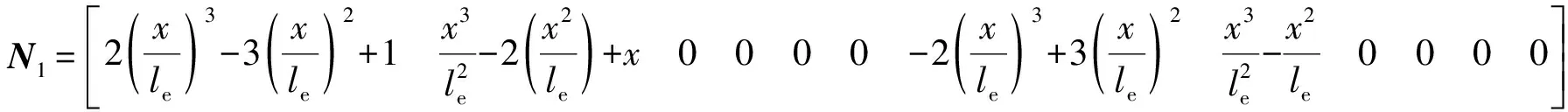
(11a)
(11b)
(11c)
(11d)
(11e)
(11f)
将上述形函数分别用于式 (4), (5), (9) 和 (10)中,则黏弹性层的位移可以通过形函数和节点位移向量表示如下
uv=N7Δe
(12a)
wv=N8Δe
(12d)
β=N9Δe
(12c)
εv=N10Δe
(12d)
式中
(13a)
(13b)
(13c)
(13d)
1.4 单元刚度阵
单元刚度矩阵由单元势能导出。本部分将用到的数学术语意义如下:Ei,Ai,Ii和ρi(i=c,v,b)分别为约束层,黏弹性层和基梁的弹性模量,横截面积,惯性矩和密度;Gv为黏弹性层的剪切模量。
(1) 弹性层(约束层和基梁)势能
弹性层由轴向位移引起的势能为
(14a)
(14b)
弹性层由横向位移(弯曲)引起的势能为
(15a)
(15b)
(2) 黏弹性层势能
黏弹性层由剪应变引起的势能为
(16a)
(16b)
(17a)
(17b)
黏弹性层由压应变引起的势能为
(18a)
(18b)
显然,单元总势能为各层势能之和
(20)
单元总刚度阵为各层刚度阵之和
(21)
(22)
1.5 单元质量阵
单元质量阵由单元动能导出。
各层因轴向运动引起的动能为
(23a)
(23b)
式中,为各层轴向运动相应的质量阵。
各层因横向运动引起动能为
(24a)
(24b)
式中,为各层横向运动相应的质量阵。
显然,单元总动能为各层动能之和
T=Tei+Tbi,(i=c,v,b)
(25)
单元总质量阵为各层质量阵之和:
(26)
1.6 黏弹夹芯梁有限元动力学方程
哈密尔顿(Hamilton)原理的变分形式可表示为
δ(T-U)dt+δWdt=0
(27)
式中,T为单元的总动能;U为单元的总势能;W={Δe}T{Re}为作用于单元的非保守力所作的功,{Re}是作用于单元的外力矢量,δ为在指定时间区间内所取的变分。将式(20)和式(25)代入式(27)可以导出单元的动力学方程。
(28)
将黏弹夹芯梁离散成一定数量的有限元单元,然后按有限元单元组装的方法将这些单元的质量阵和刚度阵组装后可得黏弹夹芯梁的整体动力学方程
(29)
式中,M是夹层梁的总质量阵,K是总刚度阵,R是系统所受激励力。
2 黏弹性材料的模型
要对黏弹夹芯梁结构进行振动有限元分析,还需要建立黏弹性材料本构模型,然后将其导入到动力学方程中才能得到其固有频率和损耗因子。黏弹性材料的模型有很多种,此处只介绍下文将要使用的两种典型模型:复常数模量模型和GHM模型。
2.1 复常数模量模型
复常数模量模型认为黏弹性材料复剪切模量的实部(储能模量)和虚部(耗能模量)均为常数,即
Gv=G′+jG″=G′(1+jηv)
(30)
式中,ηv=G″/G′是黏弹性材料的损耗因子。
因为复常数模量模型的表达式是复常数,所以黏弹夹芯梁方程(29)的特征值问题为
([K]-ω*2[M]){Δ}=0
(31)
式中,ω*为特征频率,为复数,求解上述特征值问题即可求得该复特征频率,则黏弹夹芯梁系统的固有频率和损耗因子可以由下式计算
(32)
复常数模量模型形式简单,处理方便,应用较为广泛,但它没有考虑黏弹性材料的剪切模量随着振动频率变化而变化的特性。
2.2 GHM模型
GHM模型[23-24]将黏弹材料的复剪切模量函数表示成一系列微振子项的代数和。微振子项由一个虚拟的弹簧-质量-阻尼单元构成,它通过辅助座标“Z”与系统的空间坐标耦合,以此来模拟黏弹性材料与位移q相应的应力应变行为。在GHM模型中,黏弹性材料的复剪切模量函数在拉氏域中的表达式为
(33)
式中,常数G∞为当时间t=∞时,松驰函数的稳态值,即黏弹材料剪切模量的最终值。s为拉普拉斯算子。N是微振子的项数,由复剪切模量频率依赖性的高低决定,一般情况下,当频率范围在1~500 Hz时,三项微振子就能很好地满足黏弹材料复剪切模量的曲线拟合要求。每项微振子的效应由一个二阶有理函数确定,而该函数是由三个正常数{αk,ωk,ζk}确定的,因而这三个正常数也决定了复剪切模量函数在拉氏域中的形状。显然,如果取N阶微振子,该模型有3N+1个参数需要确定,这些参数可以通过对实验数据进行曲线拟合得到。
将黏弹夹芯梁结构单元动力学方程进行拉氏变换得
(34)
式中,为黏弹性材料复模量模型。
黏弹性材料复模量模型采用GHM模型时,引入辅助耗散坐标
(35)
式中:k=1,2,3,…,N为微振子项数。
然后进行拉氏逆变换并进行整理后可得黏弹夹芯梁在时域中的动力学模型为
(36)
式中
(37a)
(37b)
(37c)
(37d)
(37e)
经单元组集后即可行黏弹夹芯梁结构的动力学方程
(38)
式中,M,D和K分别为总质量阵、总阻尼阵和总刚度阵,x为总的位移量,R为黏弹夹芯梁所受外部激励力。
可见GHM模型可以很好地描述黏弹性材料剪切模量随着频率变化的特性,并且可以很好地融入到有限元动力学方程中,通过引入耗散坐标可以将黏弹夹芯梁的动力学方程转化为普通的二阶定常线性系统动力学方程,求解固有频率、阻尼等模态参数都很直接方便[25]。
3 数值验证
分别应用本模型对不同边界条件,不同几何参数的黏弹夹芯梁的振动进行分析,计算其固有频率和损耗因子,然后将计算结果分别与精确解析解、常规数值解进行对比,一方面可以多角度地验证本文提出的有限元模型另一方面也可以对黏弹夹芯梁进行振动分析,得到一些有益工程的结论。
3.1 固支-自由边界条件下黏弹夹芯梁结构的振动特性
为了研究黏弹夹芯梁结构在固支-自由边界条件下振动特性并验证本文模型,选用一根悬臂黏弹夹芯梁为研究对象,其材料和结构参数见表1。
本部分采用五种算法研究黏弹夹芯梁固有频率和损耗因子。这五种方法分别为本文的有限元模型、经典的“六阶理论”解析法[26]、“实特征模态”(Real Eigenmodes, RM)法[27]、 “钻石法”(Diamant Approach,DA)[28]和“渐近数值法”(Asymptotic Numerical Method,ANM)[29]。应用本文有限元模型时,将黏弹夹芯梁离散为30个单元。

表2和表3分别列出了上述各方法对固支-自由边界的黏弹夹芯梁前6阶固有频率和损耗因子的预测结果及与解析解的相对误差。为考察黏弹性材料损耗因子ηv对系统振动特性的影响,计算时分别取其值为0.1,0.6,1和1.5。

表2 固支-自由边界EVEC梁前6阶模态对应的固有频率计算值
从表2可以看出,在对固支-自由边界条件下的黏弹夹芯梁前6阶固有频率的计算上,本文有限元模型、RM、DA和ANM均具有良好的精度。但相比较而言,本文有限元模型的精度是最高的,与解析法相比,其误差范围为0~0.15%,平均误差为0.08%;DA法次之,其误差范围为0~0.19%,平均误差为0.12%;再次是ANM法,其误差范围为0~3.08%,平均值为1.36%;精度最低的是RM法,其误差值最低为0,最高为8.17%,平均误差为1.15%。需要指出的是,RM法计算的固有频率与黏弹性材料的损耗因子无关,这与实际不符。所以就对黏弹夹芯梁固有频率的预测上,以上四种方法的精度按高低排序为:本文模型> DA>ANM>RM。

表3 固支-自由边界黏弹夹芯梁前6阶模态对应的损耗因子计算值
从表3可以看出,在对固支-自由边界条件下的黏弹夹芯梁前6阶模态对应的损耗因子的预测上,本文有限元模型、DA法和ANM的精度都非常高。相比而言,精度最高的是本文有限元模型,其最小和最大误差分别为0和2.6%,平均误差为0.42%。排名第二是的DA法,其误差范围为0~2.6%,平均值为0.45%。ANM法的误差范围为0~10%,平均值为2.27%,排名第三。精度最差的是RM法,其误差最低为0%,最高为85%,平均误差为8.46%。当黏弹性材料损耗因子变大时,RM法对损耗因子的预测误差明显增大,当黏弹性材料损耗因子为1.5时,RM法预测的1阶损耗因子误差达到了85%,显然已经不适用了。由此可得出结论,在对黏弹夹芯梁结构的损耗因子预测上,四种数值法按精度排序为本文有限元模型> DA>ANM>RM。
表2和表3的计算结果显示本文有限元模型对固支-自由边界条件下黏弹夹芯梁结构的振动特性有良好的预测精度。另外还可以看出,黏弹性材料损耗因子增加会导致夹芯梁的固有频率和损耗因子相应增加,但其损耗因子的增加比固有频率的增加要明显得多。
3.2 简支-简支边界条件下黏弹夹芯梁结构振动特性
仍取表1中的结构参数,只是将边界条件换成简支-简支。以Rao[30]的解析解为基准,验证本文有限元模型对简支边界条件下,不同黏弹性材料损耗因子的黏弹夹芯梁结构的固有频率和损耗因子的预测精度。当采用本文有限元模型计算时,同样将梁划分为30个单元。计算结果列于表4。
从表4可以看出,在对简支黏弹夹芯梁结构的前6阶固有频率的预测上,本文有限元复合模型与解析法的结果非常接近,平均相对误差仅仅为0.23%。在对损耗因子的预测上,本文复合模型与解析解的平均相对误差仅为0.85%。可见本文模型对黏弹夹芯梁结构的振动特性预估具有良好的精度。
另外与简支-自由边界条件相比,简支-简支边界条件下黏弹夹芯梁的固有频率更大。就损耗因子而言,简支边界条件下的黏弹夹芯梁的第1阶损耗因子比简支-自由边界条件下的的要高,但其它阶的损耗因子要低。这说明不同的边界条件对黏弹夹芯梁的振动特性有较大影响。

表4 简支-简支边界黏弹夹芯梁前6阶模态对应的固有频率和损耗因子
值得注意的是本文复合模型对这两种边界条件下的黏弹复合梁结构的固有频率和损耗因子的预测结果都非常好,这说明本文复合模型对黏弹夹芯梁的振动特性预估有良好的适用性。
4 实验验证
为验证本文有限元模型,对一黏弹夹芯梁进行振动测试实验。表5为黏弹夹芯梁的材料和几何参数。中间夹芯层材料采用国产的ZN-1型黏弹性材料。在图5为实验装置示意图。夹芯梁一端被夹具夹持,另一端自由。在自由端的中线上黏贴一微型轻质加速度传感器。实验时采用一把自制的轻质,柔软的带橡皮头小锤轻击梁端部激振,自由端的加速度信号由加速度传感器拾取,通过LMS SCADAS III数据采集器进行采集和调理,然后通过LMS Test. Lab 振动噪声试验分析系统完成信号分析,得到夹芯梁自由振动响应和响应谱。这样梁的固有频率可以从响应谱图直接读出,相应的损耗因子可由半功率法得到。表7为本文有限元模型对黏弹夹芯梁前三阶固有频率和损耗因子计算结果和实验结果的对比。计算时将梁离散成30个单元。

用本文有限元模型进行数值计算时,黏弹性材料的本构模型采用GHM模型。ZN-1型黏弹性材料GHM模型参数见表6[31]。


图5 黏弹夹芯梁结构振动测试实验装置示意图

从表7可以看出,本文有限元模型计算结果和实验结果吻合得相当好。对黏弹夹芯梁前三阶固有频率的预测误差均在3%以下,对应损耗因子的预测误差在5%以下。这说明本文有限元模型是正确的。
5 结 论
基于复合耗能假设建立了一种新的有限元数值模型研究黏弹夹芯梁的振动和阻尼特性。该模型构造的有限元单元为三层二节点梁单元,每个节点12个自由度。建模时同时考虑了中间黏弹性层的剪切阻尼和压缩阻尼。为了验证该有限元模型的有效性,引入了两个算例研究不同边界条件下黏弹夹芯梁的振动特性,结果表明本文提出的有限元复合模型的计算精度优于几种常用数值方法,对不同边界条件的黏弹复合梁均有良好的适用性。最后还通过对黏弹夹芯梁结构的振动实验对本文有限元模型进行了验证,结果表明本文有限元模型是正确可靠的。

