全下肢直接数字X线摄影推算四川汉族女性身高

崔井会，骆莹贞，常云峰，彭钊，邓莉萍，张奎，邓振华

（1.四川大学华西基础医学与法医学院，四川 成都 610041；2.中南大学基础医学院法医系，湖南 长沙410013；3.四川大学华西医院，四川 成都 610041）

个体身高的推算是法医学研究与实践中一项重要的基础性工作，特别是在如爆炸、碎尸、高度腐败及白骨化等不能进行DNA身源鉴定的案件中。近年来，随着人口流动的增加，我国无名尸体案件亦随之增加，对骨骼个体识别的需求日益迫切。为了满足案件侦查的需要，国内学者[1]开始引用国外的有关研究成果，对中国人骨骼个体识别的方法进行了广泛深入的研究。随着经济的发展，国人体质有了整体提高，同时受地域、种族、性别、年龄和个体差异的影响，身高推算的研究已成为常规性研究。而我国身高推算相关研究中的研究样本多来源于20世纪80年代，用于当代国人身高推算准确性较低。因此，建立适合当代国人身高的推算模型就显得格外重要。

1899年，PEARSON[2]首次将长骨长度与身高进行回归分析，得出了利用股骨推断身高的数学模型，成为法医学中推断身高的经典方法。此后，有许多国内外学者[3-7]利用四肢长骨及长骨碎片针对不同的种族与人群建立了相应的身高推算数学回归模型。研究结果均显示，四肢长骨与身高的相关性较高，并以利用股骨进行身高推算最为准确。我国利用四肢长骨进行身高推断的研究大多采用尸体或干骨，样本量偏少，特别是对女性身高推断的研究，而且利用影像学方法进行身高推断大部分针对的是未成年人[4-5，8-9]。因此，本研究旨在采用直接数字X线摄影（direct digital radiography，DDR）技术，测量四川地区汉族女性全下肢相关指标，构建当代国人身高推算的数学回归模型，为法医学实践积累基础数据。

1 材料与方法

1.1 研究对象

本研究的所有样本均来自四川大学华西医院，共收集四川地区汉族健康女性全下肢DDR图像样本171例。

纳入标准：（1）籍贯为四川；（2）健康女性；（3）汉族；（4）所拍摄DDR图像质量清晰，可清楚观察到测量标志点。

排除标准：（1）下肢有骨折、畸形或手术史者；（2）曾经服用或正在服用影响骨代谢与生长发育的药物者；（3）患有影响骨生长、发育与代谢的全身性疾病者。

本研究符合医学伦理学相关规定。

1.2 方法

1.2.1 身高测量

在摄片前，按照《体质测定》中身高测量方法[10]、用SZG型身高坐高计（南通悦健体测器材有限公司）测量每个个体的身高（y，cm），精确至0.1cm。

1.2.2 DDR图像采集

采用大平板多功能数字化透视/摄影系统［Sonial Vision SafireⅡ，岛津企业管理（中国）有限公司］拍摄，条件为：管电压70～95kV，管电流250～400mA，曝光时间5.0～8.0 ms，固定球管中心至成像板的距离为120cm。拍摄体位：仰卧负重站立位（检查者光脚仰卧于检查床上，双足分立于脚踏板上，足尖向前，双下肢伸直，髌骨位于膝关节正前方，检查床与水平面成40°～45°夹角，X射线球管与检查床垂直）。采用系统自带的Syngo-Imaging VB36C图像后处理软件进行图像后处理及测量，精确至0.1cm。

1.2.3 观测指标

本研究参照传统法医人类学骨骼测量方法，结合全下肢DDR影像特点选取左下肢以下骨性标志点及测量指标（图1）。

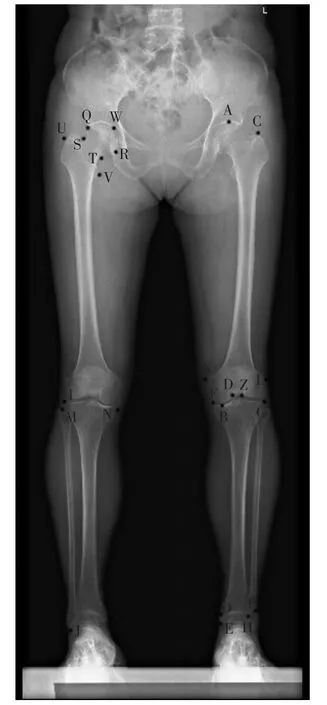
图1 DDR图像上的测量标志点

股骨最大长（x1）：股骨头最高点（A）至内外侧髁最低点（B）之间的垂直距离；

股骨生理长（x2）：股骨大转子最上点（C）至内外侧髁最低点（B）之间的垂直距离；

胫骨最大长（x3）：胫骨髁间棘最高点（D）至内踝最低点（E）之间的垂直距离；

胫骨内侧最大长（x4）：胫骨内侧平台最内上缘点（F）至内踝最低点（E）之间的垂直距离；

胫骨外侧最大长（x5）：胫骨外侧平台最外上点（G）至胫骨外侧最下点（H）之间的垂直距离；

腓骨最大长（x6）：腓骨头最上点（I）至外踝最下点（J）之间的垂直距离；

髁间宽（x7）：股骨内外侧髁最外侧点（K与L）之间的水平距离；

胫骨平台最大宽（x8）：胫骨平台两侧最外侧点（M与N）之间水平距离；

胫骨远端最大宽（x9）：胫骨远端两侧最外侧点（O与P）之间的水平距离；

股骨头最大宽（x10）：股骨头最外上点（Q）与股骨头最内下点（R）之间距离；

股骨颈最小宽（x11）：股骨颈最狭窄处宽度（S与T之间距离）；

股骨大小转子间最大宽（x12）：大转子最外侧点（U）与小转子最内侧点（V）之间距离；

股骨头最大长（x13）：股骨头最内上点（W）到线段UV的垂直距离；

内侧髁间棘（Z）至内侧平台最内上点之间水平距离（x14）：D与F之间距离；

外侧髁间棘至外侧平台最外上点之间的水平距离（x15）：Z与G之间距离。

对由于体位等原因造成左下肢测量标志点遮挡或者不清晰的图像测量右下肢。171例样本中，139例测量单侧下肢，32例测量双下肢。

1.2.4 统计方法

应用SPSS 21.0统计学软件，首先对总体样本的身高、年龄及各测量指标进行描述性统计分析，对身高及各测量指标进行单样本Kolmogorov-Smirnov检验，分析其是否符合正态分布。采用配对样本t检验分析32例双侧下肢测量值之间的差异性。从样本中随机选取15例，由同一测量者对测量指标进行2次测量（2次测量时间间隔大于1月），采用独立样本t检验进行一致性检验。以各指标为横坐标，身高为纵坐标绘制散点图，观察测量指标与身高之间是否存在线性关系。分析各测量指标与身高的相关性（r），利用相关性较高的测量指标建立身高推算的一元线性回归方程。考虑到不全长骨或骨骼测量标志点缺失的情况，纳入多个测量指标采用逐步回归分析的方法建立多个多元线性回归方程。身高推算的逐步回归方程，就是将测量指标逐个引入回归模型，每引入一个新的测量指标都对已入选回归模型的指标逐个进行检验，将经检验认为不显著的指标删除，以确保每次引入新指标之前回归方程中只包含显著性指标，经过反复的入选与删除，直到既没有显著的指标选入方程，也没有不显著的指标从方程中剔除为止，以保证最后所得到的测量指标的集合是最优的。检验水准α=0.05。

1.2.5 回代检验

按照纳入标准重新收集29例样本，回代检验上述回归方程的准确性。

2 结 果

描述性统计分析显示，样本年龄11.0～79.0岁，平均年龄47.6岁，平均身高（153.5±6.7）cm。各测量指标与身高的描述性分析结果见表1。

表1 年龄、身高及各测量指标的描述性分析（n=171）

配对t检验显示，双侧下肢的测量值之间差异无统计学意义（P＞0.05）。一致性检验显示，同一测量者两次的测量结果之间差异无统计学意义（P＞0.05），具有一致性。

所有测量指标（x1～x15）及身高均符合正态分布。x1与身高的相关性最高（r=0.856）；x2～x6与身高具有较高的相关性，r由高到低依次为：x6（0.836）＞x5（0.829）＞x3（0.828）＞x2（0.825）＞x4（0.821）；x10、x12、x13与身高的相关性偏低，r分别为0.459、0.494、0.525；其余的测量指标（x7～x9，x11、x14、x15）与身高的相关性较差，r在 0.044（x14）～0.348（x11）。

利用相关性较高的测量指标建立一元线性回归方程6个（表2），所有方程均有统计学意义（P＜0.05），复相关系数（R）为0.821～0.856，标准估计误差（standard error of estimate，SEE）为3.453～3.812cm。利用所有测量指标，采用逐步回归分析方法建立身高推算多元线性回归方程4个（表3），所有方程均有统计学意义（P＜0.05），R为0.874～0.897，SEE为2.994～3.258 cm。单独应用股骨或胫骨的测量指标采用逐步回归分析方法建立身高推算的多元线性回归方程3个（表4），所有方程均有统计学意义（P＜0.05），R为0.837～0.875，SEE为3.254～3.662cm。

运用以上身高推算数学模型，对29例回代检验样本的身高进行推算，结果显示，所有身高推算方程的平均绝对误差为（2.485～3.432）cm，±1SEE准确率在35.7%～60.7%，±2SEE准确率为75.0%～92.9%。回代检验准确率最高的检验结果见表5。

表2 利用单个测量指标（x1～x6）建立的身高推算一元线性回归方程

表3 利用所有测量指标采用逐步回归分析方法建立的身高推算多元线性回归方程

表4 利用股骨或胫骨测量指标采用逐步回归分析方法建立的身高推算多元线性回归方程

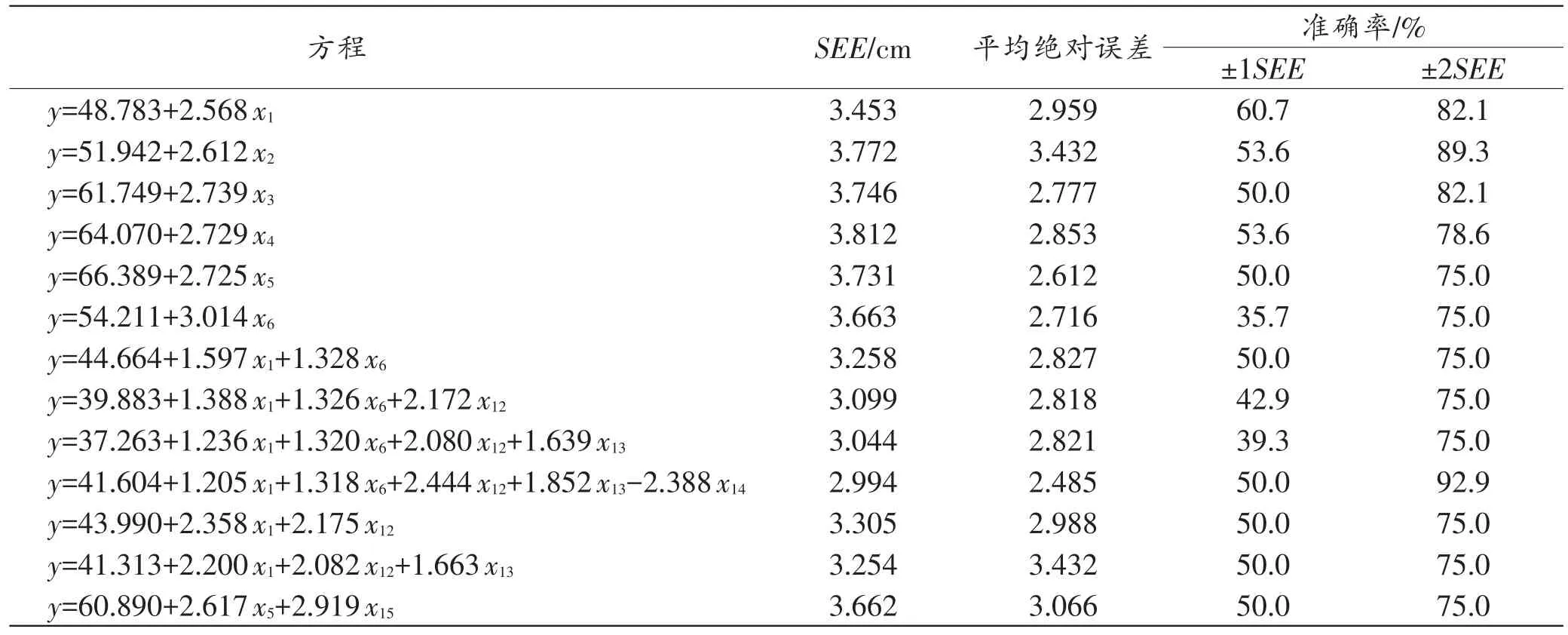
表5 方程准确率回代检验结果

3 讨 论

身高推算作为法医学个体识别中的重要组成内容，一直是国内外学者研究和关注的重点之一。早在1899年就已有利用股骨进行身高推算的研究[2]，建立了利用股骨进行身高推算的回归方程，并成为身高推算的经典方法。为了更加适应实际检案的需要，自20世纪60年代开始，陆续有学者对残存长骨进行测量研究，以期找到利用部分长骨或长骨碎片进行身高推算的方法：2002年，张继宗[8]建立了中国女性不完整长骨推断身高的回归方程；2007年，CHIBBA等[3]应用胫骨近端及远端测量指标构建了不完全胫骨的身高推算方程；2001年，李铁英等[11]建立了基于股骨、胫骨、尺骨、肱骨骨性标志测量值的多元回归方程，同时考虑到长骨近端、远端或两端同时缺失的情况。以上研究的样本都来自尸体或者干骨，由于受到样本来源的限制，大多数研究样本量较小。也有学者探索利用体表解剖标志进行身高推算的方法：2003年，OZASLAN等[9]通过测量转子高度、大小腿长度、足长等活体体表指标建立了身高推算模型；2013年，NOR等[12]也做了相似的研究，并得出了相似的结论。利用体表标志点进行身高推算方法简单易行，在一定程度上突破了样本量的限制，建立的身高推算模型也更加适合当代人群，但不能忽略受软组织等影响造成测量误差的存在。随着医学影像技术的发现与发展，其在骨骼成像及测量方面的优势迅速显现并很快应用于法医人类学的研究。X线摄影技术是一种非破坏性的检查方法，重复性好，X线片易存储，在法医人类学中主要通过对活体、尸体或含有骨骼的肢体的影像学资料进行年龄、性别以及身高的推断。1962年，TELKKA等[13]应用长骨X线片对儿童进行了身高推算。2007年，周晓蓉等[4]应用X线摄影技术对上肢长骨与身高的关系进行了研究。2017年，BRITS等[14]应用磁共振技术对青少年股骨与身高的关系进行了研究。利用放射学方法进行身高推算的研究是以活体为研究对象，样本来源范围广，样本量不受限制，能够清晰显示测量标志点，使测量结果更加准确。

我国应用数字化X线摄影技术进行身高推算的研究少，受X线摄影机曝光范围所限，研究主要局限于青少年，并且主要研究胫腓骨或股骨。郑涛等[5]应用357例14～18周岁青少年的肱骨、尺桡骨及胫腓骨计算机X线摄影（computed radiography，CR）片（其中肱骨及尺桡骨94例，胫腓骨163例）建立了身高推算回归方程，结果显示，女性组回归方程的R为0.710～0.895，SEE为（3.075～4.084）cm。范涛等[15]测量了422例（男207例，女215例）CR片的胫腓骨长度指标，建立了不同性别、不同年龄段身高推算的一元线性回归方程35个，其中女性组回归方程的R为0.827～0.850，SEE为（2.68～2.86）cm。以上研究均以CR片为研究对象，存在横向和纵向上的放大问题，虽然都经过校正，但操作方法相对复杂。本研采用的是全下肢正位DDR图像，不存在放大率问题，不需要校正，操作相对较简单。本研究所有测量指标中，股骨、胫骨、腓骨长度相关指标与身高具有较高的相关性，并以股骨最大长度与身高的相关性最好，这与既往的研究结果[5-7，11-14]一致。利用全下肢相关指标建立一元线性回归方程6个，多元线性回归方程7个，所有方程的R在0.821～0.897，SEE在 2.994～3.812 cm。与郑涛等[5]的研究结果相比，本研究所用的样本量较大，且所得线性回归方程的R及SEE均较高；与范涛等[16]的研究结果相比，R较高，但SEE较大，这可能与本研究样本中包含未成年人而范涛等的研究样本均为成年人有关，同时地域差异的影响也不能排除。经检验，所有方程的平均绝对误差为（2.485～3.432）cm，±1SEE准确率为35.7%～60.7%，±2SEE准确率为75.0%～92.9%，方程准确性较高，并以方程y=41.604+1.205x1+1.318x6+2.444x12+1.852x13-2.388x14的平均绝对误差最小（2.485 cm），±2SEE准确率最高（92.9%）；方程y=48.783+2.568x1的±1SEE准确率最高（60.7%）。回代检验表明，多元回归方程准确性优于一元回归方程，多指标推算优于单指标。

本研究采用大平板多功能数字化透视/摄影系统采集全下肢正位图像，拍摄体位与身高测量体位相似，保证了拍摄图像时身高与站立时身高的一致。该设备拍摄的图像具有一次性采集、图像清晰、分辨率高、图像锐利、解剖标志点清晰等特点，同时还具有强大的图像后处理功能，能直接在其工作站上进行窗宽、窗位的调整，测量角度、距离等，同时具有便于存储、传输等特点，非常适用于临床研究及检案鉴定工作。同时，该成像系统采用了狭缝式同步扫描技术原理，很好地解决了纵向放大率的问题，使测量值与真实值一致，并且其扫描范围广，能一次性完整地呈现全脊柱、全下肢等图像，特别适合于法医人类学研究工作，且可应用于碎尸案或无名尸体解剖检验前的影像检查，在法医人类学研究方面具有广阔的应用前景。

本研究利用影像学技术，以活体为研究对象进行身高推算，所建立的回归方程平均绝对误差较小，同时考虑到下肢单块骨、多块骨及骨骼碎片的情况，具有较强的实用性。但由于未成年人进行全下肢摄影检查者较少，使样本收集较困难，本次并未做针对性研究，同时本次的研究样本具有一定的地域、民族、性别的特异性，其他地区或民族的身高推算应用该方程具有一定的局限性，需做进一步研究。