混凝土梁柱极限挠度和裂缝宽度计算

涂好祖 （安徽天成建设有限公司，安徽 六安 237000）

0 前言

典型的受弯构件正截面试验梁一般为单筋矩形截面简支梁，该梁应具有足够的抗剪能力，以保证在受弯实验中不发生剪切破坏。其加载方式为集中荷载跨中加载，荷载逐级加载，由零开始直至梁正截面受弯破坏，此时跨中变形最大，即为最大挠度，同时也是最大裂缝宽度出现的位置。在实际工程中，由于荷载作用位置的不准确性，混凝土的非均匀性和施工偏差等原因，都可能使结构构件的偏心距加大，钢筋混凝土柱采用柱顶水平力与竖向力加载方式，模拟工程实践中可能出现的柱偏心受压以及受到剪力的受力状态，计算柱的最大挠度和最大裂缝宽度。图1为梁在集中荷载下的加载图，图2为柱在水平荷载和竖向荷载作用下的加载图。

图1 集中荷载加载图

图2 柱加载图

1 构件基本参数

混凝土使用C30,梁截面尺寸为250mm×250mm,净跨为5m,保护层厚度c=20mm，纵筋和箍筋都为HRB400 混凝土材料参数：fc=14.3N/mm2，fck=20.1N/mm2，ft=1.43N/mm2，ftk=2.01N/mm2，EC=3.00 ×104N/mm2，ho=460mm。钢筋材料参数：fy=360N/mm2，ES=2.00×105N/mm2。

2 单筋矩形截面梁最大挠度和最大裂缝计算

2.1 正截面承载力基本计算公式

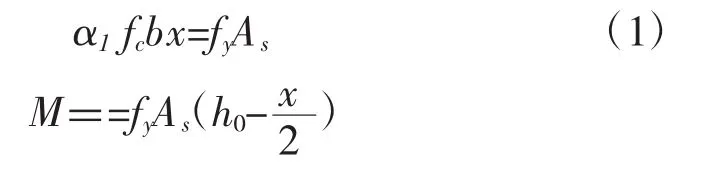
式中:α1混凝土强度等级小于获等于C50时,取α1=1.0。纵筋面积 As=1256mm2。由公式（1）可计算出构件能承受的最大弯矩和最大剪力。代入求得最大弯矩为 179.507kN·m,最大剪力为 71.8kN。

2.2 斜承载力基本计算公式

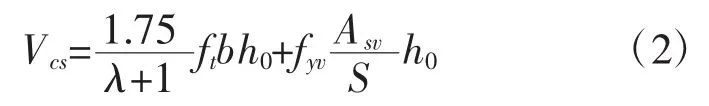
式中：λ为计算截面的剪跨比，λ=a/h0,a为集中荷载作用点距支座截面或节点边缘的距离；当λ<1.5时取1.5；当λ>3时取3。由公式（2）可计算箍筋。截面配筋见图3。

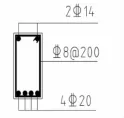
图3

2.3 刚度计算公式

式中:Bs为钢筋混凝土梁开裂后的短期刚度，由于不考虑荷载的长期作用，即不考虑受压区混凝土发生的徐变，所以采用短期刚度；Ψ为裂缝间纵向受拉钢筋应变不均匀系数，当Ψ<0.2时取0.2，当Ψ>1.0时取1.0，对直接承受重复荷载的构件取Ψ=1.0；γf'为受压翼缘加强系数，对矩形截面，γf'=0。

由公式（3）可以计算出钢筋混凝土梁开裂后的短期刚度BS=3.15×1013N·mm2

2.4 变形和裂缝宽度计算公式

式中：αcr为构件受力特征系数，对受弯、偏心受压构件，取αcr=1.9；对偏心受拉构件，取αcr=2.4；对轴心受拉构件，取αcr=2.7；CS为最外层纵向受拉钢筋外边缘至受拉区底边的距离，当CS<20mm时，取CS=20mm;当 CS>65mm 时，取 CS=65mm。由公式（4）计算得跨中最大挠度变形为11.872mm;由公式（5）计算得最大裂缝宽度为0.414mm。

3 对称配筋柱受压计算

同时承受轴力和弯矩的构件为偏心受压构件，轴力N和弯矩M的共同作用等效于一个偏心距e0=M/N的偏心压力的作用，因此偏心受压构件不仅是最基本、应用最广泛的构件之一。如图2所示的钢筋混凝土柱受到水平力P和竖向轴压力N的作用，相当于偏心受压。柱在给定轴压比、纵筋、箍筋的条件下验算其承载力，计算其最大变形、最大裂缝宽度。柱截面配筋见图4，纵筋单侧配筋率为0.6%，即As=942mm2；全部纵筋配筋率为1.2%,在要求范围内（0.5%～5.0%)。

图4

3.1 N和e的计算

给定的轴压比为λ=0.4，由此计算出轴力N、e,基本公式如下。

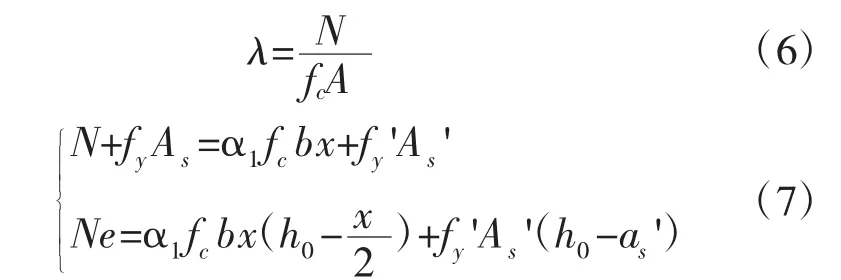
求得N=915200N,e=399mm

3.2 对称配筋时大小偏心的判别

将（7）式求得的结果代入可判断柱为大偏心受压。

3.3 水平力P的计算

由（7）式求得的e可以求出柱承受的弯矩M，依据M可求出所能承受的等效水平力P.基本公式如下。

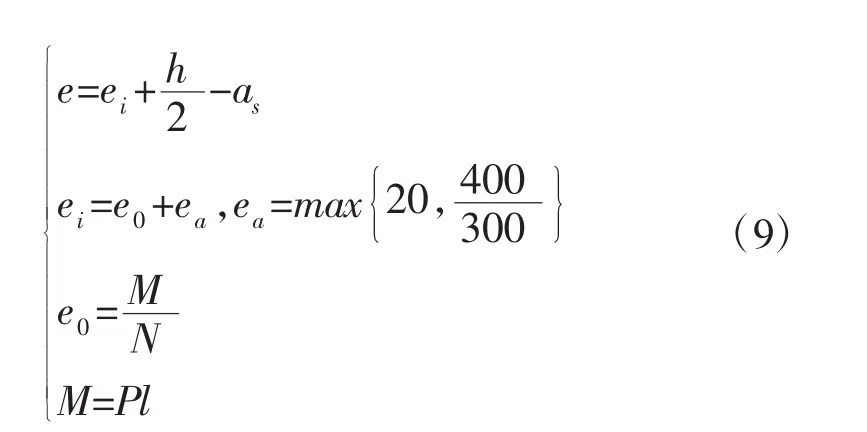
由上式求得：M=200.429kN·m，P=67kN。

3.4 箍筋的验算

在给定箍筋配筋的情况下须验证柱子能承受的最大剪力，柱子两端在压力的作用下对其抗剪能力有一定的提高，量化后具体为0.07N（Nmax为0.3fcA）

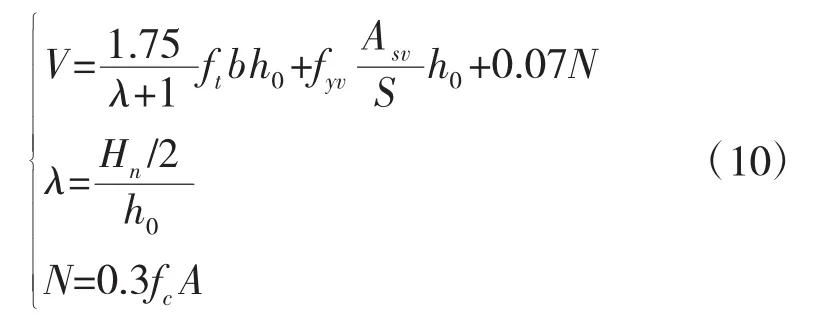
由上式求得柱子能承受的最大剪力为204kN,大于水平力P，故柱子抗剪能力满足要求。

3.5 最大变形和最大裂缝宽度计算

由图5（a）所示，柱最大变形发生在柱顶,根据结构力学图乘法可求得变形量大小,如图5（b）所示。

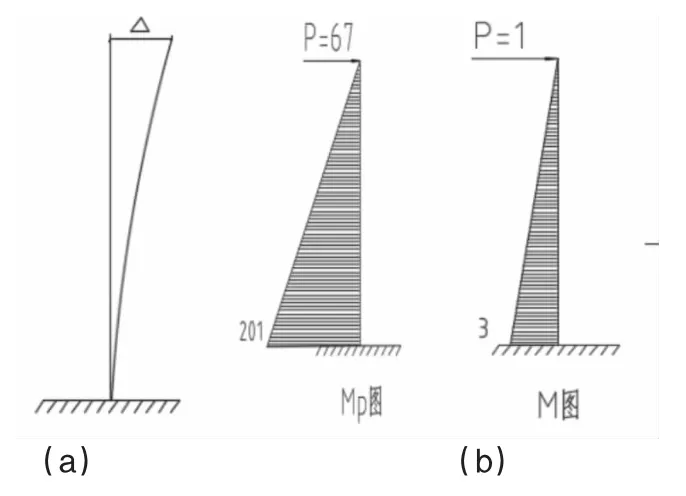
图5

3.5.1 短期刚度Bs计算

不考虑荷载的长期作用，即不考虑受压区混凝土的徐变，故构件刚度采用短期刚度。

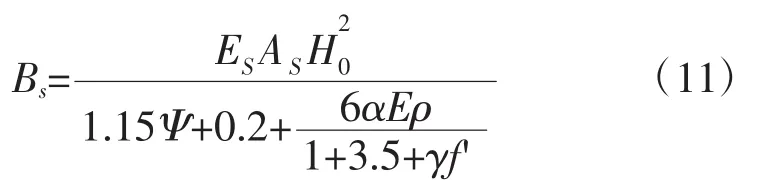
式中：Bs为钢筋混凝土梁开裂后的短期刚度，由于不考虑荷载的长期作用，即不考虑受压区混凝土发生的徐变，所以采用短期刚度；Ψ为裂缝间纵向受拉钢筋应变不均匀系数，当Ψ<0.2时取0.2，当Ψ>1.0时取1.0，对直接承受重复荷载的构件取Ψ=1.0；γf'为受压翼缘加强系数，对矩形截面，γf'=0。

由公式（3）可以计算出钢筋混凝土梁开裂后的短期刚度BS=1.76×1013N·mm2

3.5.2 挠度公式

式中：A为任一弯矩图面积，y0取自另一图形形心处对应于直线图形处的高度，EI构件抗弯刚度，即本构件的短期刚度Bs.求得最大挠度为34.26mm,最大挠度出现柱顶。

3.5.3 最大裂缝宽度公式

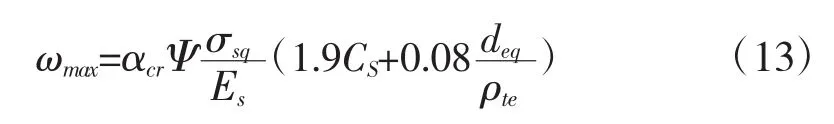
式中：αcr为构件受力特征系数，对受弯、偏心受压构件，取αcr=1.9；对偏心受拉构件，取αcr=2.4；对轴心受拉构件，取αcr=2.7；CS为最外层纵向受拉钢筋外边缘至受拉区底边的距离，当CS<20mm时，取CS=20mm;当 CS>65mm 时，取 CS=65mm。由公式（14）计算得最大裂缝宽度为0.54mm。

4 结语

利用混凝土基本原理中的构件的正截面设计和斜截面设计等原理和结构力学基本方法的结合，可以验算构件配筋的合理性，计算最大挠度、最大裂缝出现的位置及大小，通过具体的实验得出的结论为工程实践提供一定的参考。