一种简化脉冲耦合神经网络的高分辨率农村公路影像分割方法

王智灏，刘亚岚，任玉环，李娅

(1.中国科学院遥感与数字地球研究所，北京 100101；2.中国科学院大学，北京 100101)

0 引言

党的十七届三中全会通过的《中共中央关于推进农村改革发展若干重大问题的决定》中明确提出了对发展农村交通运输的目标、任务和要求，并且国务院常务会议将农村公路建设作为当前进一步扩大内需、促进经济增长的十项措施之一。由于农村公路点多、线长、面广，传统调查手段是地方上报和实地抽检，数据可能存在漏报、虚报，而实地抽检耗时长且有诸多触不到的“死角”，使得农村公路管理成为“老大难”问题。

近几年来，随着信息技术与传感器技术的快速发展以及无人机的大量使用，从不同卫星系统、航空飞机和无人机所获得的遥感图像在空间分辨率、光谱分辨率和时间分辨率上均有了大幅度的提高，所以高分辨率遥感技术为提高农村公路建设和监管水平提供了强有力的数据支撑。但是也正是由于图像的高空间分辨率，在表现出更多精细信息的同时增大了噪声对农村公路提取的影响，给农村公路的精确提取带来了挑战。另外，一般的分割方法由于公路与其他地物相连不易分割，容易产生过分割现象，导致农村公路提取精度不高。

脉冲耦合神经网络(pulse coupled neural network，PCNN)是一种基于猫的视觉原理构建的简化神经网络模型[1]，该方法已经广泛应用于图像平滑、图像分割、图像细化、边缘检测和路径跟踪各个方面[2-3]，并取得了显著成果[4-8]。尤其是在图像分割应用中，PCNN能够较好地分离目标和背景部分的重叠[4]。但是，由于PCNN模型中存在着各个参数，参数值的变化决定着 PCNN的运行结果，这使得原始的PCNN算法应用于公路分割需要进行多个参数的不断调试，过程过于繁琐，难以找到规律。

鉴于此，本文采用典型的简化PCNN算法，并结合最小交叉熵方法自适应生成迭代次数，最后再通过形态学方法进行完整的农村公路图像分割。

1 方法

1.1 PCNN模型

PCNN神经元模型由若干个分支PCNN的神经元互连组成，构成PCNN的单个神经元由树突、非线性连接调制、脉冲产生三部分构成[9]。基于对PCNN模型神经元进行操作进而完成对输入图像进行分析、处理的目的，最终得到输出图像。整个脉冲耦合神经网络的工作过程可以总结为：当神经元有脉冲输出时，其动态门限瞬间增大；当门限增大到无法产生脉冲输出时，门限便开始指数衰减；而当门限衰减至小于它的内部活动项时，脉冲会再次发生，周而复始。明显可以看出，这些脉冲串从输出再输入到与其相连的其他神经元树突上，进而又对这些神经元的激发状态有着影响。

经典PCNN的数学公式描述如下：

(1)

式中：Sij表示神经元的外部刺激；Fij表示神经元的输入部分；Lij表示连接输入；Uij表示神经元的内部活动项；Yij表示神经元的输出；θij表示动态阈值；αF、αL为衰减时间常数，决定F、L通道的衰减速度；αθ为阈值衰减时间常数，控制着阈值的下降速度，αθ越大，阈值衰减得越快，模型运行次数越少。相反，αθ越小，阈值衰减得越慢，模型运行次数越多；Vθ为阈值幅度系数，它是阈值的幅度调整常量，在调节神经元的点火周期长短方面有着重要的作用。当神经元点火时，该值确定了阈值被提升的高度。VF、VL均为链接幅值系数，它们是链接域的幅度调整常量，它们能够按照一定的比例缩放邻域内的点火神经元对中心神经元传递的能量，同样对邻域内的所有神经元具有提升作用。β为链接强度系数，对周围神经元影响中心神经元点火周期的程度起着调节作用。在链接域未被调制前起到对其按比例缩放的作用。较大的链接系数能引起较大范围的脉冲同步。mijkl、wijkl均为链接权矩阵，可以相应地支配邻域内每个神经元对中心神经元所做贡献的大小，神经元对中心神经元所传递的能量因为距离的不同而不同。

从PCNN的数学公式可以看出，PCNN模型中存在着各个参数，参数值的变化决定着PCNN的运行结果，多个参数的不断调试过程过于繁琐，难以找到规律。

1.2 简化的PCNN模型

鉴于经典PCNN算法存在参数设置繁琐的问题，本文采用简化的PCNN模型。典型简化的PCNN模型[10]如公式(2)所示。

(2)

式中：i，j为神经元的标号;n表示迭代次数;Sij表示神经元的外部刺激;Fij表示神经元的输入部分;Lij表示连接输入;Uij表示神经元的内部活动项;Yij表示神经元的输出;Eij表示动态阈值;αE表示阈值衰减时间常数;βij表示连接强度系数;Wijkl表示加权系数矩阵;VL、VE表示放大系数常数。

1.3 基于简化的PCNN模型的农村公路分割方法

1)最小交叉熵。本文采用最小交叉熵[11-13]来决定简化PCNN模型中最优迭代次数。设有两个概率分布M={m1，m2，…，mN}和V={v1，v2，…，vN}，它们的交叉熵可表示为：

(3)

式中：M和V分别表示分割前图像和分割结果图像，当M和V相等时，D等于零。交叉熵为下凸函数，能够分别计算目标之间的交叉熵以及背景之间的交叉熵，将其和作为原图像和分割图像之间的交叉熵，定义为：

(4)

式中：

其中t为图像灰度值，h(t)为图像的灰度统计直方图；Z为灰度上限；T为阈值初值，μ1(T)和μ2(T) 均为类内均值，分别表示在该阈值下目标和背景的平均灰度值。

在计算中，对公式D(M:V:T) 采用归一化处理，因为它是在给出假定一个阈值情况下的原始图像和分割结果图像之间的信息量差异的度量结果，在迭代过程中，计算每次迭代后输出的二值图像与分割前原图像的交叉熵是否达到最小，使得分割前后图像信息量差异最小，而获得的最小交叉熵时的迭代次数。因此能够在图像灰度范围内搜索T值，将使D(M:V:T)最小的t值为最佳分割阈值，而此时的迭代次数n即为最佳的迭代次数。

2)形态学处理。运用形态学获取每块目标的面积值，算法内部给出一个假定的面积值，当目标的面积值大于假定的面积值时，赋值为1，当目标的面积值小于假定的面积值时，赋值为0。公式为：

(5)

式中：θ为设定的面积值，area为图像中区域面积的大小，当大于θ时，图像像素赋值为1，当小于θ时，图像像素赋值为0。

图1所示为本文提出的农村公路分割的技术路线。

图1 方案流程图

对输入的彩色遥感图像进行灰度化处理，使彩色图像变为灰度图像，并显示变换后图像；采用最小交叉熵方法计算分割目标之间的目标交叉熵以及背景之间的背景交叉熵，将目标交叉熵与背景交叉熵之和作为原始图像和分割后图像之间的交叉熵，并通过迭代的方法得到最优分割阈值及最优迭代次数n；对简化的脉冲耦合神经网络模型参数赋值，并基于所述最优分割阈值及最优迭代次数n对遥感图像进行分割，形成包括目标的初始分割结果；利用形态学处理方法对上述初始分割结果计算各个目标物的面积并与预先设定的面积值进行对比，去除小于该面积的目标物，最后得到最终分割结果。

2 结果与分析

本文基于分辨率为0.2 m的无人机影像，选择不同形状(笔直的农村公路，弯曲的农村公路，交叉的农村公路)和有复杂背景干扰(通过林地的农村公路，穿过房屋的农村公路，穿过耕地的农村公路)的几组农村公路影像，利用基于简化PCNN模型的方法开展村公路的图像分割，并与经典算法区域生长法和Hough变换直线检测方法比较，对分割结果进行对比分析。在定量评价中，本文使用混淆矩阵[14]来对分割结果进行精度评价，选用的主要精度指标有总体精度和Kappa系数，最后对本文提出的方法、区域生长法和非监督分类3种方法的农村公路分割结果进行定量分析的精度评价比较。

2.1 不同形状的农村公路

对于笔直农村公路图像提取结果如图2所示。从图中可以看出，3种算法都能将公路分割提取出来，但是Hough变换直线检测出现过分割现象。

图2 笔直的农村公路

对于弯曲农村公路图像提取结果如图3所示。从图中可以看出，3种算法都能将公路分割提取出来，但是Hough变换直线检测出现过分割现象。区域生长法所分割的公路与本文中基于简化PCNN模型算法相比，公路边缘粗糙。

图3 弯曲农村公路

对于交叉农村公路图像提取结果如图4所示。从图中可以看出，Hough变换直线检测和区域生长法都无法将公路正确地分割提取出来，都出现了过分割现象，并且区域生长法所分割出来的公路边缘较为粗糙。

图4 交叉农村公路

2.2 有复杂背景影响的农村公路

对于耕地中的农村公路图像提取结果如图5所示。从图中可以看出，Hough变换直线检测和区域生长算法都出现了过分割现象。而PCNN分割效果无过分割现象。

图5 耕地中的农村公路

对于穿过房屋的农村公路图像提取结果如图6所示。从图中可以看出，基于简化PCNN模型算法可以很好地将公路与居民点分开并将公路分割提取出来，而Hough变换直线检测和区域生长法无法将两者区别开，从而出现过分割现象。

对于穿过森林的农村公路图像提取结果如图7所示。图中可以看出，三者都能将公路很好地分割提取，但是本文中的方法可以更为完整的将公路分割提取。

图6 穿过房屋的农村公路

图7 穿过森林的农村公路

2.3 精度评价

为定量评价本文中基于简化PCNN方法的农村公路分割结果精度，本文使用混淆矩阵来对分割结果进行精度评价。鉴于非监督分类[15]是目前运用较多的自动分类方法，研究中对本文提出的方法、区域生长法和非监督分类3种方法的农村公路分割结果进行定量分析评价。选用的主要精度指标有总体精度和Kappa系数，精度评价结果如表1所示。

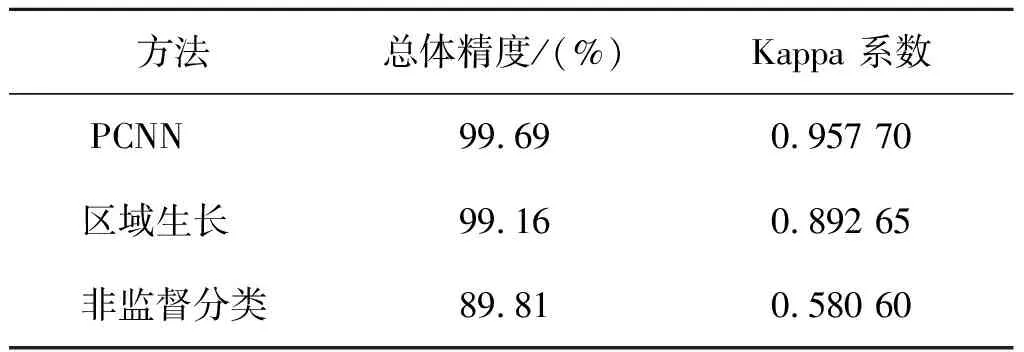
表1 不同方法的精度对比

从表中可以进一步看出本文所提出的方法无论是在总体精度上，还是在Kappa系数上，都能得到较好的分割效果，并且与原始图像的一致性较好。

3 结束语

本文在简化的PCNN的基础上，利用最小交叉熵方法自动确定最佳迭代次数，并结合形态学方法完成对农村公路的分割提取。通过对不同类型的农村公路进行分割，并对分割结果进行验证，得到较为理想的结果。相对于传统的区域生长法以及Hough变换直线检测，本文提出基于简化PCNN模型方法能够更好地将高分辨率遥感影像中的农村公路分割出来，避免了因周围噪声的影响而出现过分割的现象，且分割出的公路边缘光滑，更符合实际。定量评价结果也显示，本文方法的农村公路分割精度高于目前常用的公路分割方法，并且与原始图像的一致性较好。

当然，本文的方法仍存在一些不足，图像边缘存在欠分割现象，并且由于算法需要进行多次迭代，使得分割效率较低，如何解决这些问题，有待于后续进一步研究。