基于聚类索引的多关键字排序密文检索方案

杜瑞忠 李明月 田俊峰

(河北大学网络空间安全与计算机学院 河北保定 071002) (河北省高可信信息系统重点实验室(河北大学) 河北保定 071002) (drzh@hbu.edu.cn)

云计算被认为是企业IT基础设施的新模式，该模式可以组织庞大的计算，提供可用的、便捷的、按需的网络访问，进入可配置的计算资源共享池存储和应用资源.尽管云服务具有各种优势，但将敏感信息外包给远程服务器也带来了隐私问题.这些隐私安全威胁严重阻碍了云计算的发展.现有的加密技术可以保障云环境下的数据在可预见时间里的安全性，但这些复杂的加密技术使搜索加密数据变得困难，限制了外包数据的可用性[1].因此，如何在保护用户隐私的同时，使云数据获得有效的检索是亟待解决的问题.

可搜索的加密方案使客户能够将加密的数据存储到云中，并通过密文域执行关键字搜索.文献[2]提出了第1个基于密文扫描思想的可搜索加密方案，该方案对单个关键词的查询需要扫描整个文件，因此检索的效率低.文献[3]提出了对称可搜索加密的正式安全定义，并设计了一个基于Bloom过滤器的方案.该方案搜索时间是O(m)，m是文档数量.文献[4]提出了实现最优搜索时间的2种方案(SSE-1和SSE-2).其中，SSE-1方案对于选择关键字攻击是安全的，SSE-2对于自适应选择关键字攻击是安全的.但上述方案只是用于单关键字的查询，即用户在一次查询中仅能提交1个查询检索词，在功能方面非常简单.

相对于单关键字查询，多关键字查询允许用户输入多个查询关键字来请求需要的文档，可以更好地满足用户的查询需求.文献[5]提出了多关键字排序密文检索问题，通过计算文件向量和查询向量内积的结果进行排序.但是此方案没有考虑关键字权重的问题，查询向量与结果集文件的相关度不高，即检索精度不高.文献[6]在文件排序时用余弦相似度代替内积来计算文件向量与查询向量的相似度，同时引入TF/IDF(term frequency/inverse document frequency)算法，提高了检索精度，但缺乏对频率信息和实际搜索性能的安全性分析.文献[7]应用了稀疏矩阵的方法实现了安全的大规模方程.文献[8]提出细粒度的多关键字检索方案，采用分类子词典技术以及偏好因子提高了检索效率.为了方便用户查看检索结果，文献[9]提出了一个支持排名搜索安全的多关键字密文排序检索方案，该方案基于二叉平衡树构建了索引，但在生成索引树时该方案随机选取2个结点生成父结点，将文档之间的相关性忽略，降低了检索精度，同时为了得到top-K个文件在最坏的情况下要遍历整个索引树.

受到以上工作的激励，本文在多关键字密文检索框架上提出基于聚类索引的多关键字排序密文检索方案(multi-keyword ranked ciphertext retrieval scheme based on clustering index, CTMRSE).在构建索引树前用改进的Chameleon算法对文件进行动态聚类，通过制定阈值来限制聚类的过程，最后按照聚类结果构建索引树，直到生成根结点.查询的过程利用检索算法自上而下查询.当访问的结点不是叶子结点时，选择与查询向量相似度最高的结点访问；当访问的结点为叶子结点时，利用排序算法按相似度高低将文件插入列表；如果列表中文件数量少于K，回溯到其父亲结点访问，否则直接返回列表.该检索方法降低了查询的时间复杂度，提高了检索效率.

本文的主要贡献体现在3个方面：

1) 在聚类前通过记录关键字位置对文件向量进行降维，降低了聚类过程中不必要的计算消耗，减少了聚类时间.

2) 在动态聚类Chameleon算法中引入了杰卡德相似系数来计算高维文件向量之间的相似度以及设定合适的k值与minMex值来提高在高维空间中聚类结果的质量，从而提高检索精度.

3) 提出新型密文检索结构CTMRSE及相应的算法，通过理论分析与实验验证了该方案提升了多关键字密文检索的效率和精度.

1 背景介绍

1.1 系统模型

本文的系统模型如图1所示，将云服务按功能不同可以分为3个实体：数据拥有者、数据使用者和云服务器.

1) 数据拥有者.数据拥有者即数据的属主方，要搜集数据、数据分类、建立聚类索引以及加密和上传数据与索引.此外，数据拥有者需要给数据使用者合理授权，分享密钥.

2) 数据使用者.数据使用者为数据拥有者授权的用户，要设定返回的文档数K，然后将查询的内容生成陷门TD发送给云服务器，在获得返回的K个文档后，使用共享密钥对文档进行解密.

3) 云服务器.云服务器为密文检索提供了大量的计算和存储资源,接到数据使用者合法的查询请求时,云服务器需要根据查询算法以及利用索引树进行计算，返回和查询最相关的前K个文档.

Fig. 1 The architecture of search over encrypted cloud data图1 密文检索的系统架构图

1.2 模型威胁分析

为了规范研究范围，本文假设云服务器诚实但是好奇，即云服务器会按着用户的要求执行操作，但它会试图分析用户的数据与索引从而获取用户的隐私信息.主要考虑2种威胁模型[10]：

1) 密文已知

云服务器只知道数据拥有者上传到云端的加密后的文档集C、索引树T和陷门TD.

2) 背景已知

在背景已知模型中，云服务器不仅知道密文已知模型中的信息，还配备统计信息功能，可以通过分析相应频率分布的直方图，进行TF统计攻击，推断甚至识别某些关键词.

1.3 主要符号说明

本文使用的主要符号说明如下.

F: 明文文档集合{f1,f2,…,fm}；

C: 密文文档集合{c1,c2,…,cm}；

W: 关键词集合{w1,w2,…,wn}；

I: 安全索引集合{I1,I2,…,In}；

QW: 查询向量；

TD: 查询关键词陷门；

m: 文档集合文档数量；

EK: 返回的结果集；

k: 最近邻数量；

M: 一个聚类中最多容纳文件个数；

u: 为了文档的安全性添加的维数；

n: 关键词集合中关键词的个数；

K: 用户指定返回的文档个数.

1.4 Chameleon算法

Chameleon算法[11]是一种层次聚类算法，其运作模型如图2所示，图2中的每个顶点代表1个文件对象，每个文件对象用n维向量来表示，连接2个顶点边的权值为这2个文件之间的相似度.聚类过程分为3个步骤：用k最近邻算法构建稀疏图，k值对算法的结果会产生很大影响，要设定适当的取值；在保证割边最小化的情况下，将图划分成多个小簇；使用凝聚层次聚类算法，基于子簇的相似度反复合并子簇，其中，minMex(度量函数阈值)取值过小容易发生过拟合，较大则导致近似误差增大，因此也要设定合理值.其中，度量函数为RI(ci,cj)×RC(ci,cj)α.当α>1时，表示更重视相对近似性；当α<1时，表示更重视相对互连性；当α=1时，表示2个量度标准有相等的权重.

Fig. 2 The operation model of Chameleon algorithm图2 Chameleon算法的运作模型

1.5 结果集排序隐私度

排名隐私度[12]可以量化搜索结果向云服务器的信息泄漏量：

/K2，

(1)

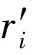
2 改进的Chameleon算法

2.1 向量降维

在建立索引前对文件集向量进行聚类用到的是Chameleon聚类算法.选择该算法来聚类是因其在聚类的过程中不仅考虑每个簇之间的互联性，而且考虑簇的邻近性，动态聚类结果质量高，可提高后期检索效率与精度.但Chameleon算法聚类代价较高，为了降低聚类时间对文档向量进行降维处理.

每个文件对应1个n维的文档向量，文件包含的关键词在向量中对应的位置为1，其他位置都为0.一个文件一般只会包含极少量的关键词[13]，即每个n维的文档向量中包含大量的0，文档向量之间的相似度计算会带来不必要的开销.因此，将高维向量通过记录关键词的位置进行降维处理可减少不必要的计算消耗，从而提高聚类的效率.假设关键词数n=1 000，则每个文档向量的维度为1 000，通过记录关键词的位置降维，每个位置只需要用10位二进制来表示.如图3所示，向量D1和D2分别为文件1与文件2的文件向量，D1向量中的1对应的位置为8,35,255,985，即文件1包含关键词集中的4个关键词{w8,w35,w255,w985}.D2向量中的1对应的位置为8,35,129,255,768，即文件2含有关键词集中的5个关键词{w8,w35,w129,w255,w768}.图3为通过记录关键词位置将向量D1和D2转化为向量A1和A2的过程，随着文件向量的维数增加，基于位置降维效果会更明显，聚类效率相应提高.

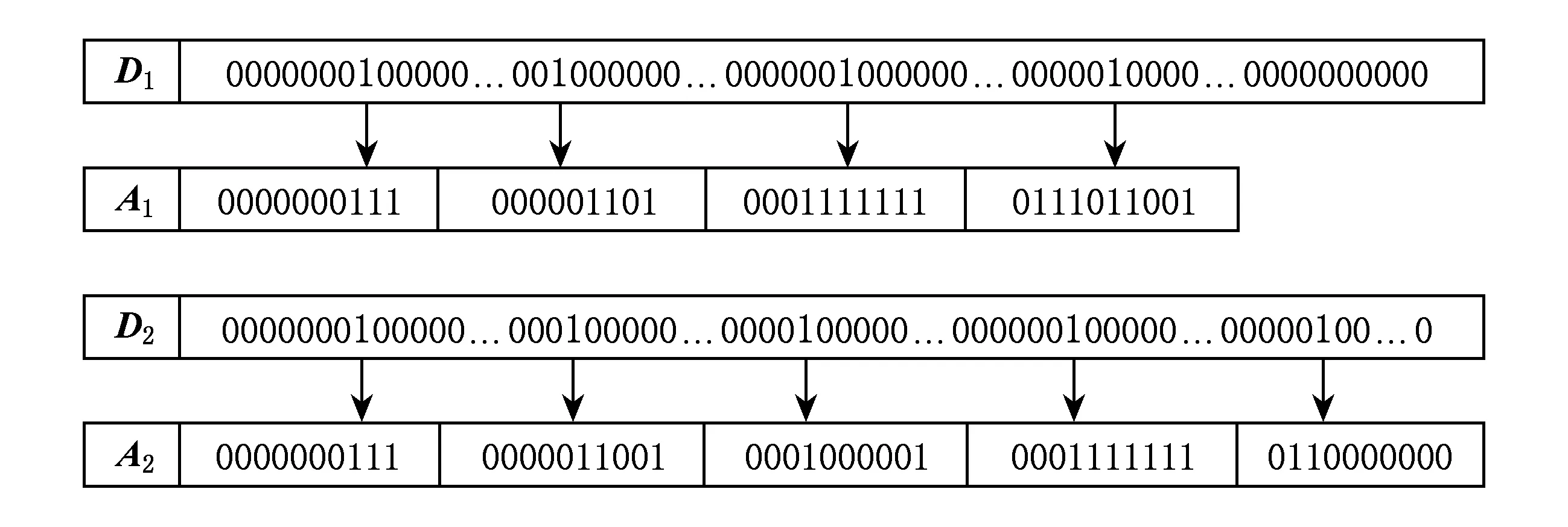
Fig. 3 The dimensionality reduction process of D1 and D2图3 文件向量D1与D2的降维过程

2.2 相似度

在Chameleon算法中利用k邻近算法构建稀疏图时，连接2个边的权值是2个文件向量的相似度(邻近图中的文件向量是经过降维处理的).为了在高维空间得到有意义的簇，提高聚类结果的质量，引入杰卡德相似系数计算经过降维处理的文件向量之间的相似度.杰卡德相似系数是衡量2个集合相似度的一种指标，用杰卡德相似系数计算高维向量之间的相似系数时，用J(D1,D2)表示：

(2)

其中，p是文件1与文件2包含相同关键字的个数；q是文件1包含文件2不包含关键字的个数；r是文件2包含文件1不包含关键字的个数；s是文件1与文件2都不包含关键字的个数.

文件向量D1与D2经过降维后得到A1与A2，如图3所示，J(D1,D2)可以通过向量A1与A2来计算，由于A1与A2记录着文件1与文件2包含关键字的位置，且相同的关键字在文档向量中对应的位置相同，可通过对比记录的关键词的位置即可迅速的计算出p,q,r,s的值，不需要对比向量A1与A2的每个比特位，在提高聚类质量的同时也提升了聚类效率.例如图3中文件向量D1和文件向量D2之间的杰卡德相似系数为14.

2.3 改进的Chameleon算法

在Chameleon算法中引入杰卡德相似系数来计算文件向量之间的相似度以及在聚类过程中通过记录关键字位置对文件向量进行降维处理后的算法如下.

算法1. 改进的Chameleon算法.

输入: 文件集合F；

输出: 聚类结果.

① for each filefiin clusterCido

Di←RedDimPro(fi)；

d←JaccardCoef(Di,Dj)；

if (d=MinDistance&&Num≤k) then

Connection(Di,Dj)；

Num++；

end if

end for

② Builtk-nearest graph；

③ for each clusterCiinClusterList

Ci,Cj←EC(Ci)；

EC(Ci,Cj)←AbsolutInter(Ci,Cj)；

EC(Ci)←Inter(Ci)；

RI(Ci,Cj)←Relative(Ci,Cj)；

SEC{Ci,Cj}←AbsolutClose(Ci,Cj)；

SEC{Ci}←InterClose(Ci);

RC(Ci,Cj)←RelativeClose(Ci,Cj)；

tempMetric=max{RI(Ci,Cj)×RC(Ci,Cj)}；

minMex←SetThreshold；

if (tempMetric>minMex) then

NewCi←Merge(Ci,Cj)；

else

DeleteCifromClusterList；

end if

end for

在算法1中，RedDimPro(fi)为文件fi生成文档向量，并对文档向量进行降维的函数；JaccardCoef(Di,Dj)为用杰卡德相似系数来计算文件向量Di和Dj之间相似度的算法.RI(Ci,Cj)定义为簇Ci和Cj的互联度:

(3)

RC(Ci,Cj)定义为簇Ci和Cj相对近似度:

(4)

利用改进的Chameleon算法对文件向量聚类可提高聚类质量，从而提高检索精度.此外先聚类再建立索引可提高检索的效率.

Fig. 4 The process of clustering图4 聚类过程

2.4 聚类结果

为了更好地显示聚类过程，从文件集合{f1,f2,…,fm}中选取了12个文件，根据改进的聚类算法将文件动态聚类得到D,E,F,H,G这5个簇.图4为文件向量映射在2维平面上的效果图，其中簇D,E,F相似度分数高，将E,F,D这3个簇聚为一类(即B)，类似地，也可将簇H,G聚为一类(即C),A为B和C的总和.

3 方案构建

3.1 基本方案

1)SK←setup(1n,u)

数据拥有者从{f1,f2,…,fm}中提取出n个关键词集{w1,w2,…,wn}.然后，随机生成一个(n+u+1)维的向量S作为分割指示向量，同时生成2个(n+u+1)×(n+u+1)可逆矩阵M1和M2，组成密钥SK={S,M1,M2}.

2)I←Genindex(F,SK)

在生成文档向量前，数据拥有者计算关键词权重[10]：

(5)

3)TD←GenTrapdoor(QW,SK)

Fig. 5 The process of index tree encryption图5 索引树加密过程

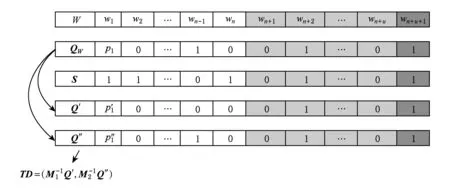
Fig. 6 The process of trap generation图6 陷门生成过程

4)EK←Query(I,TD,K)

通过陷门TD，云服务器利用检索算法自上而下进行检索，先计算陷门与根结点所有孩子结点的相关度得到相关度最高的子结点，然后访问该子结点的所有孩子结点，以此类推直到找到目标簇，如果该簇的文件量小于返回文件数K，回溯到其父亲结点，遍历其兄弟结点的孩子结点，直到找到相似度分数最高的前K个文档向量，返回给数据使用者.

其中，相关度分数的计算：

(6)

5)FK←Dec(EK,SKf)

数据使用者接收到云服务器返回的密文EK后利用密钥SKf解密，得到明文FK.

3.2 索引构建

根据聚类结果构建索引树的算法如下.

算法2. 构建聚类索引的算法.

输入: 文件集F；

输出: 根结点rootNode.

MakeIndexTree(F)

①InitQueue(*Q)；

② for each documentfi∈Fdo

v←Di；

EnQueue(SqQueueQ,QElemv)；

end for

③ while ((QueueLength(SqQueueQ)>1)do

for eachdatainQdo

Ci←Chameleon(Q->data)；

end for

end while

④ for each clusterCido

Comput Cluster CenterMi；

ParentNodePN←Mi；

if ((Q->rear+1)%MaxSize=Q->front)then

return 0；

else

EnQueue(SqQueueQ,QElemPN)；

N←QueueLength(SqQueueQ)；

DeQueue(LinkQueue *Q,N,NodeSet)；

end if

end for

rootNode←Q->data；

returnrootNode.

在算法2中，QueueLength(SqQueueQ)为求队列Q长度的算法；EnQueue(SqQueueQ,QElemPN)是将元素PN插入队列Q的队尾；DeQueue(LinkQueue *Q,N,NodeSet)将队列Q前N个元素全部删除，然后把删除的元素插入到NodeSet中.

3.3 检索过程

利用索引树查询的算法如下.

算法3. 查询算法.

输入: 索引树T；

输出: 搜索结果文件集Rlist.

GDFABTS(IndexTreeNode)

① ifu.childis not a leaf node then

max←0；

while(u.child)do

ComputeRScore(u.child,QW)；

if (u.child>max) then

max←RScore(u.child,QW)；

else

return

end if

end while

GDFABTS(u.child)；

② else

while (u.child) do

SORT(Rlist,u.child,RScore(u.child,QW))；

end while

ifRlist.num=Kthen

returnRlist；

else

GDFABTS(u.rightsib)；

end if

end if

在算法3中，RScore(u.child,QW)为计算结点u.child中存储的文件向量与查询向量相关分数的算法；GDFABTS(u.rightsib)为回溯算法；SORT(Rlist,u.child,RScore(u.child,QW))为按照相关分数排序的算法.

图7是由图4的聚类结果根据构建索引算法生成的索引树，以图7中的索引树为例，设K=4，n=5，查询向量QW=(0,1,0,1,1)，图7中的向量都尚未加密.从根结点A开始搜索，先计算查询向量和根结点A的2个子结点B与C的相似度分数.由于查询向量与结点C的相似度分数高，接下来搜索结点C的子结点，经过计算得到查询向量与结点H，G中G相似度最高，接着查询结点G的子结点，根据检索算法，由于G的孩子结点是叶子结点，则用直接插入算法按照相关度分数的大小依次将其插入Rlist中.要求返回4个文件，目前Rlist中只有2个文件，则回溯到结点C查询另1个孩子结点H.同样利用直接插入算法将其孩子结点按着相似度分数插入Rlist.最终返回文件的是图7中的①②③④.

Fig. 7 Index tree图7 索引树

4 检索效率、精度与安全分析

4.1 查询效率分析

Table 1 Time Complexity of Each Scheme表1 各方案时间复杂度表

4.2 检索精度分析

文档之间的关系通常被隐藏在加密过程中[15]，这将导致显著的搜索精度性能下降.较好的查询结果应该保持查询文档与文档之间的相似度，相似度越高，检索精度越高.本方案检索精度量化为

(7)

其中，K为最终密文检索返回的前K个文件，K′是明文查询中返回的前K′个文件，RScore(QW,Di)为查询向量QW与返回结果集中文档的相似度.

传统的MRSE方案在加密Di过程中以及EDMRS方案在索引构建过程的阶段将文档之间的相关性忽略，导致检索精度性能下降.经3.1节式(6)推导，CTMRSE方案中相关度分数Rscore=TD·Ii=Di·QW，即密文检索计算的相关度分数与明文检索的相同.另外，该方案在建立索引之前对文件聚类，经过检索算法搜索返回结果集的文件在同一个簇或者相邻簇，而文件的相关度与聚类质量有关，聚类质量越高搜索结果集的文件相关度越高.为了提高聚类质量，在聚类过程中引入杰卡德相似系数来计算文件向量之间的相似度以及设定合适的阈值降低误差率.因此查询向量与结果集的文件相关度高.

4.3 安全分析

1) 索引和查询保密性

CTMRSE方案用随机的(n+u+1)维向量S对文档向量Di与查询向量QW进行分割，可以保障文档在已知背景攻击模型中的索引确定性和查询保密性.同时通过矩阵M1和M2对向量进行变换的难以确定性，使保密性进一步增强.

2) 查询无关联性

向量添加了u维同时从中随机选择v维置为1，且最后1维的值被置为随机值，相同的搜索请求将产生不同的查询向量并接收不同的相关性分数分布，从而更好地保护查询无关联性.

3) 关键字隐私

云服务器能够通过分析关键词的TF分布直方图来推断识别关键词[16].CTMRSE方案采取添加维度且随机赋值的加密方式能抵抗已知背景模型中的统计攻击.

5 性能分析

本文实验使用国内云存储提供商阿里云的云存储平台(搭载centos 7.3 64位系统、主频为2.5 GHz的4核CPU、16 GB内存、内网宽带为0.8 Gbps、公网宽带为100 Mbps、系统盘为40 GB高效云盘)搭建存储系统.原型系统的开发和测试环境是基于centos 7的Linux[17]平台，具体硬件配置是intel®CoreTMi7-6700(3.40 GHz)处理器，配备8 GB内存和网速为1 Gbps的校园网环境.实验数据使用20 431篇英文新闻作为测试数据集[18]，共有20个类别，类别是非均匀的.然后通过全文检索工具Lucene[19]用分词器对纯文本字节流进行分词，滤掉26.1%的停用词(如as,but)，对这些文档进行关键词提取形成关键词数为7 200的关键词集合.

5.1 聚类效率与精度

首先为了验证改进的方案提高了聚类效率，对改进方案与未改进方案的聚类时间进行实验，实验使用m=3 000的文件集合，字典大小n=1 000.实验结果如图8(a)所示，未改进方案聚类时间比改进方案所需时间明显长.因此，用改进的方案使得聚类效率有了很大提升.图8(b)是本文方案与文献[9]中的EDMRS方案对于构建索引所需时间进行对比的实验，实验表明EDMRS方案构建二叉平衡树与本方案根据聚类结果动态构建索引树所用的时间基本保持一致.

由于k值与度量函数取值过小容易发生过拟合，较大则导致近似误差增大，对聚类结果有巨大影响，实验通过聚类结果的误差率来确定k值与minMex取值.文件数量相同时，如图9(a)当文件数量m=1 000时，k=6时误差最小.文件数量变化时，k值随着文件数量变化而改变.对应的k值也通过聚类结果的误差率来确定；minMex的取值不同得到聚类结果的误差率不同，如图9(b)所示，文件数量m=1 000，minMex=0.18时误差率最小.但minMex取值随着文件数量的变化保持不变.因此，通过对k值与minMex设定合适的取值可以使聚类结果误差率降低，提高了聚类结果质量，从而提高检索的精度.

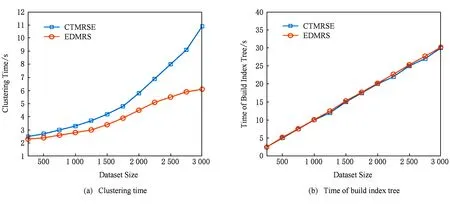
Fig. 8 Clustering effect图8 聚类效果

Fig. 9 Error ratio with the increasing thresholds图9 取不同阈值对应的误差率

5.2 检索效率

授权用户在进行检索时，总希望快速地得到检索结果，为了检测3个方案的检索效率，分别在文件数量、关键词个数以及授权用户要求返回文档数量不同时进行实验，实验结果如图10所示.由于方案MRSE查询时需要计算所有的密文文档向量和密文查询向量之间的相似度，时间复杂度为O(m)，在图10(a)中，当文档集合的文档数量按着指数级增加时，MRSE的方案的查询响应时间也呈指数级增长.而EDMRS和CTMRSE的方案的时间复杂度与索引树的层次相关，都是近似线性增长，但是相同的文件数量构建的索引树的层次CTMRSE方案比EDMRS少，因此CTMRSE方案查询时间增长更缓慢，检索效率最高；无论用户要求返回多少文件，MRSE方案没有用到索引树，需要与所有的文件向量计算相似度，再根据相似度大小进行排序，在图10(b)中检索时间几乎不变，但是该方案的检索时间最长.随着用户要求返回文档数量的增加，查询时要计算相似度的叶结点数量增多，即θ与的值增大，在图10(b)中EDMRS和CTMRSE方案的检索时间都增长，但是比较稳定.由于θ>，CTMRSE方案的查询时间最少；随着关键词集合中关键字数量的增多，在计算查询向量与文档向量的相似度时，计算时间增长，尤其是MRSE方案，要计算与所有文件向量的相似度，在图10(c)中MRSE方案增长幅度最高，查询时间最长.EDMRS和CTMRSE方案的查询时间也会随着关键词集合中关键字数量的增多而增长，图10(c)中，EDMRS和CTMRSE方案的查询时间增长的都比较稳定，CTMRSE方案的查询效率最高.

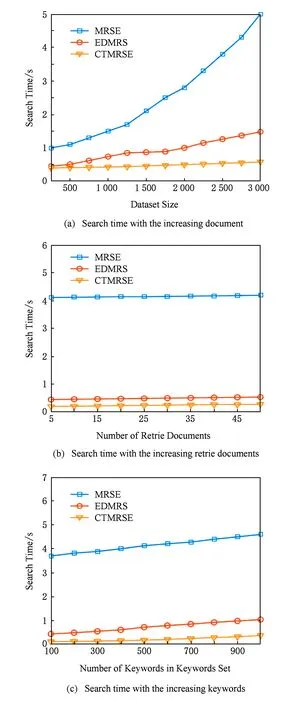
Fig. 10 Query efficiency图10 查询效率

5.3 结果集相似度与排序隐私度对比

用户不仅看重检索效率，还在乎检索的精度和隐私安全.实验通过查询向量与结果集的相似度来度量检索的精度，如图11(a)所示，当关键词数量变化时，CTMRSE方案相似度最高，具有明显优势.实验通过结果集排序隐私度检测MRSE，EDMRS，CTMRSE方案的隐私安全性，如图11(b)所示，CTMRSE方案的排序隐私更好，安全性更高.

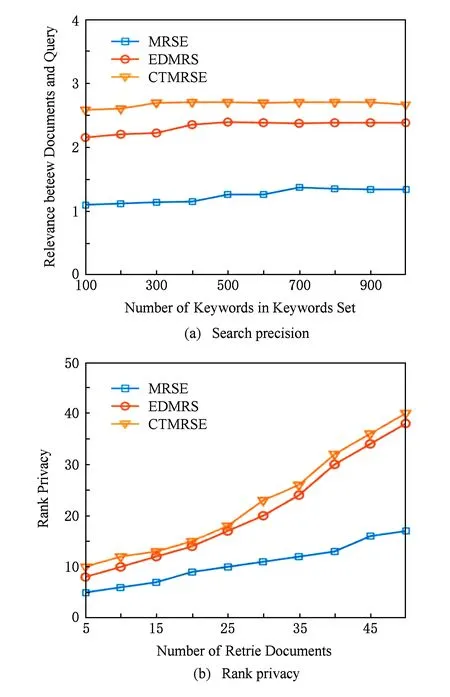
Fig. 11 Search precision and rank privacy图11 结果集相似度与排序隐私度

6 总 结

本文提出了基于聚类索引的多关键字排序密文检索方案(CTMRSE).该方案先聚类再建立索引，聚类时通过记录关键词位置对向量进行降维，减少聚类过程中不必要的计算消耗.同时，引入了杰卡德相似系数来计算高维向量之间的相似度，并给Chameleon算法设定合适的k值与minMex值减少聚类结果的误差率，提高聚类质量与检索精度.该方案还提出了相应的索引结构和相应的算法，并通过建立密文检索实验平台验证了本方案在保障数据隐私安全的同时，有效的提高了密文检索的效率与精度.但CTMRSE方案是在文件集不变的情况下进行的实验，当添加、删除和修改文件时动态更新索引树，以及数据改变后验证检索结果的真实性、完整性是未来需要进行的工作.