基于奈奎斯特定理与曲线拟合的温度计算方法

董亚楠，黄正旺，许钦涛

（豫新汽车热管理科技有限公司，河南 新乡 453049）

随着社会的进步，人们对于空调温度控制精度的要求越来越高，而原来空调控制器中采用查表的方式进行温度计算的温度算法，已经不能够适应现在空调温度控制器系统的需求。这就要求提供一种新的算法来提高温度计算，使其能够适应新的温度控制的要求。

基于奈奎斯特定理“过采样和抽取”的方法，可以在不改变原有控制器硬件电路的基础上，采用软件计算的方式将MCU的AD转换的精度在原有的基础上提高1～2倍。这样不仅可以提高空调温度控制的精度，而且可以提高对空调冷暖风门、模式风门、新风门运行角度的精度，提高鼓风机反馈电压的计算精度，有利于整个空调控制系统控制精度的提高。并且不增加产品成本和不改变空调控制器原有的硬件设计，从而能够提高产品的市场竞争力。

1 基于奈奎斯特定理的“过采样和抽取”

1.1 奈奎斯特定理的原理

奈奎斯特定理“过采样和抽取”的原理：设有一个频率带限信号x(t)，其频带限制在(0，fn)内，如果以不小于fs=2fn的采样速率对信号x(t)进行等间隔采样，得到时间离散的采样信号x(t)=x(nTs)(其中Ts=1/fs称为采样间隔)，则原有信号x(t)将被所得到的采样值x(n)完全确定。上述的奈奎斯特采样定理告诉我们，如果以不低于信号最高频率2倍的采样速率对带限信号进行采样，那么所得到的离散采样就能准确地确定原信号。下面从数学的角度来进一步证明奈奎斯特采样定理［1］。

其中x［k］=x(t)|t=Kt，Ω=ωT，连续信号x(t)的频谱为x(jω)，离散序列x［k］频谱为x(ejΩ)，其计算公式见公式 (1)、公式(2)、公式 (3)，如图1所示。

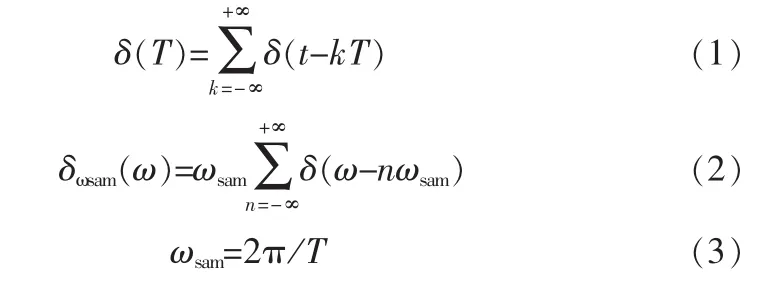
图1 δT（T）和δωsam（ω）时序图

若连续信号X(t)的频谱为X(jΩ)，离散序列X［k］频谱为X(ejΩ)，且存在x［k］=x(t)|t=Kt，则有：

信号时域的离散化导致其频域的周期变化。其中，T为抽样间隔，ωsam=2π／T为抽样角频率。X(jω)时序图如图2所示。当ωsam＞2ωm时，如图3所示；当ωsam=2ωm时，如图4所示；当ωsam＜2ωm时，如图5所示。

图2 X（jω）时序图

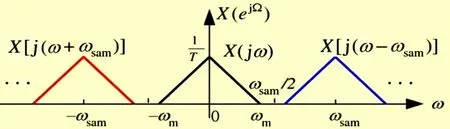
图3 ωsam＞2ωm时序图

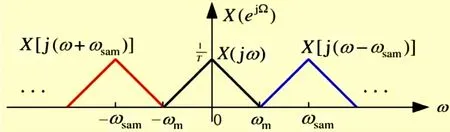
图4 ωsam=2ωm时序图

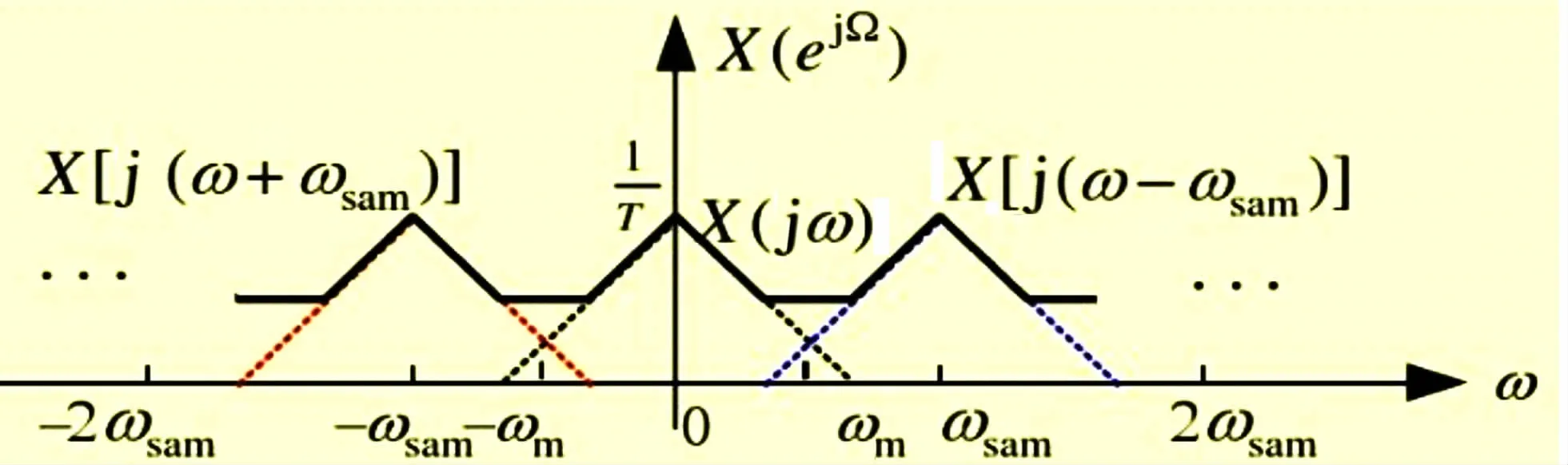
图5 ωsam＜2ωm时序图

通过公式 (1)～(7)和图2～图5的计算和图示，可以得出：如果以不低于信号最高频率2倍的采样速率对带限信号进行采样，那么所得到的离散采样就能准确确定原信号。

1.2 过采样和抽取

现在常用的MCU产品中的ADC转换器，转换的ADC数据相当于一种低通滤波器，而奈奎斯特采样定理适用于该控制器系统中。根据奈奎斯特采样定理，如果以不低于信号最高频率2倍的采样速率对带限信号进行采样，那么所得到的离散采样就能准确确定原信号。在进行ADC采样时，按照公式 (8)的形式进行。其中，fsignal是输入信号的最高频率，fnyquist是采样奈奎斯特频率的“过采样”。

根据ATMEGA644PA中数据手册中的说明，在使用其内部10位精度的ADC转换器时，其ADC的时钟频率应该在50～200 kHz，之间，本文中使用的系统时钟为8 MHz的晶振，因此在进行ADC时钟设定时采用64分频，将ADC的时钟信号圈定在125 kHz，保证其10位ADC转换值的精确。亦在ADC转换的硬件电路上的AVCC的ADC采样的基准电压输入端采用LC滤波电路，对其进行滤波处理，并在ADC转换期间，使用MCU的ADC转换休眠模式 (即：定时器T0、看门狗工作，关闭其他中断和I/O的操作，降低转换期间的系统噪声)［2］。

按照奈奎斯特采样定理本文需要按照公式 (9)的形式进行，ADC转换值的过采样。

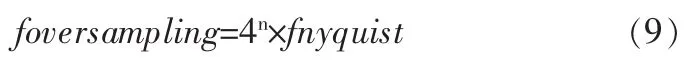
根据公式 (9)中的采样频次，如果要提高1位精度的ADC转换值需要采集4n倍的数据来进行“过采集”。即：如果将ADC从10位提高至11位其需要过采集的数据是10位精度的4倍，将ADC从10位提高至12位其需要过采集的数据是10位精度的42=16倍。具体的计算方法是：如果将ADC10提高至ADC11，需要将4个ADC10相加，这样就可以得到12位的ADC数值，其最后一位没有实际意义；需再将其右移一位或者除以2，这样就可以得到ADC11的数据。而将ADC10提高至ADC12，需要将16个ADC10相加，这样就可以得到14位的ADC数值；其最后两位没有实际意义，需再将其右移两位或者除以4，这样就可以得到ADC12的数据，这样每一位的电压分辨率可以达到1.22 mV。

这样可以得到公式 (10)用于通过计算增加ADC的分辨率［3］。

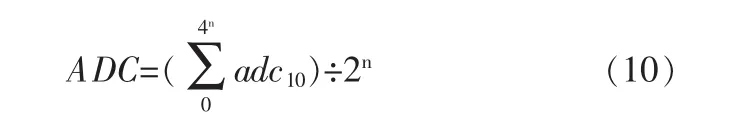
2 曲线拟合的温度计算

2.1 基于曲线拟合的温度计算

现在空调控制器系统中一般使用的非线性的NTC型负温度系数的温度传感器，其在某温度下的阻值计算公式如公式 (11)所示。

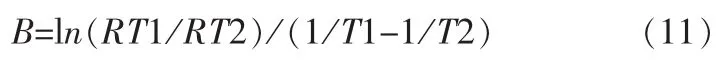
式中：RT1——热敏电阻在T1温度下的阻值；RT2——热敏电阻在T2常温下的标称阻值；B——热敏电阻的热敏指数；T1、T2——开尔文温度。

由于NTC型负温度系数的温度传感器的热敏指数在不同的温度区间其数值也会随着温度区间地上升而加大，温度区间地下降而减少的变化，因此NTC型负温度系数的温度传感器的R-T曲线为曲值不定的一条曲线段 (如图6所示，为本文用NTC型热敏电阻的R-T曲线)，而使用公式 (11)计算温度，就需要对各个温度区间的热敏系数进行计算，而只使用厂家提供的B值就会出现其温度曲线在一定温度下偏差过大的现象 (如图6所示，其中红色曲线为正确的R-T曲线，绿色曲线为使用公式 (11)计算的到的曲线，可以看出在系统温度低于10℃时，2条曲线的偏差将逐渐变大)，无法满足温度控制精确的需要。

因此，本文为解决以上问题，首先采用的是利用传感器厂家提供的R-T温度表格，建立一个对应的ADC数值表，通过和表格内的数值对应，找到ADC值处于那2个整度温度之间，然后将相邻温度的曲线段看做是一条直线，使用直线段的计算公式来计算温度。但是通过这样的方法进行计算时，分段模拟出的直线段不能与温度传感器的曲线完全贴合在一起，就会造成温度计算的偏差，而且在曲线曲度越大的温度区间内的偏差将会越大，很难达到精确控制温度的系统要求［4］。因此，在本文中采用曲线拟合的方法来进行温度计算。将图6所示的红色NTC温度传感器的R-T温度曲线分成数段，然后使用其他的曲线，并取其他曲线中与目标曲线中相符合的部分，利用数条曲线来模拟出与图6所示的红色NTC温度传感器相符合的曲线段。

图6 NTC型热敏电阻与公式（11）R-T曲线图

曲线拟合的拟合曲线的公式如公式 (12)所示，其中T为换算出的温度值，An、An-1、An-2、…、A2、A1、B为根据不同传感器阻值的换算常数，R为NTC传感器的阻值。

采用公式 (12)的数列，可以分段将数列的曲线的部分与目标曲线的部分拟合在一起。本文中采用的NTC型负温度系数的热敏电阻的传感器，参数为B25/50=3274、R25=5 kΩ。

通过计算和模拟，在本文中将目标曲线分为三段，分别是：T1为-40～0℃、T2为-5～60℃、T3为55～90℃。然后根据目标曲线的各个R-T温度表的数值，计算的曲线公式如公式(13)～公式 (15)所示。其与目标曲线的拟合如图7所示。

图7中黄色曲线为公式 (15)的曲线，红色曲线为公式(14)的曲线，绿色曲线为公式 (13)，图中的蓝色曲线为目标曲线。各个曲线通过与目标曲线的R-T温度阻值表进行计算其得到的数值与目标曲线相差0.1℃。

图7 温度传感器R-T曲线与公式（13）～公式（15）拟合曲线图

3 计算原理试验验证

本文介绍了基于奈奎斯特定理“过采样和抽取”原理与采用“曲线拟合”方式的温度计算方法，在不改变原有控制器系统硬件电路和系统整体成本的基础上，通过软件计算的方法提高了控制器对于温度控制的精度，并且该方法还可以应用在提高空调系统。对于冷暖风门、模式风门、新风风门的角度控制精度、蒸发风机的风量调整方面的精度等，有着巨大的应用潜力。

本文使用冷藏机组用控制器来测试该温度方法的准确性，如图8所示，通过酒精恒温槽如图9对控制器的温度显示进行测试。

图8 检测控制器图

图9 低温恒温槽图

通过测试其测试数据，如表1所示，其温度偏差为0.1℃，达到设计要求。

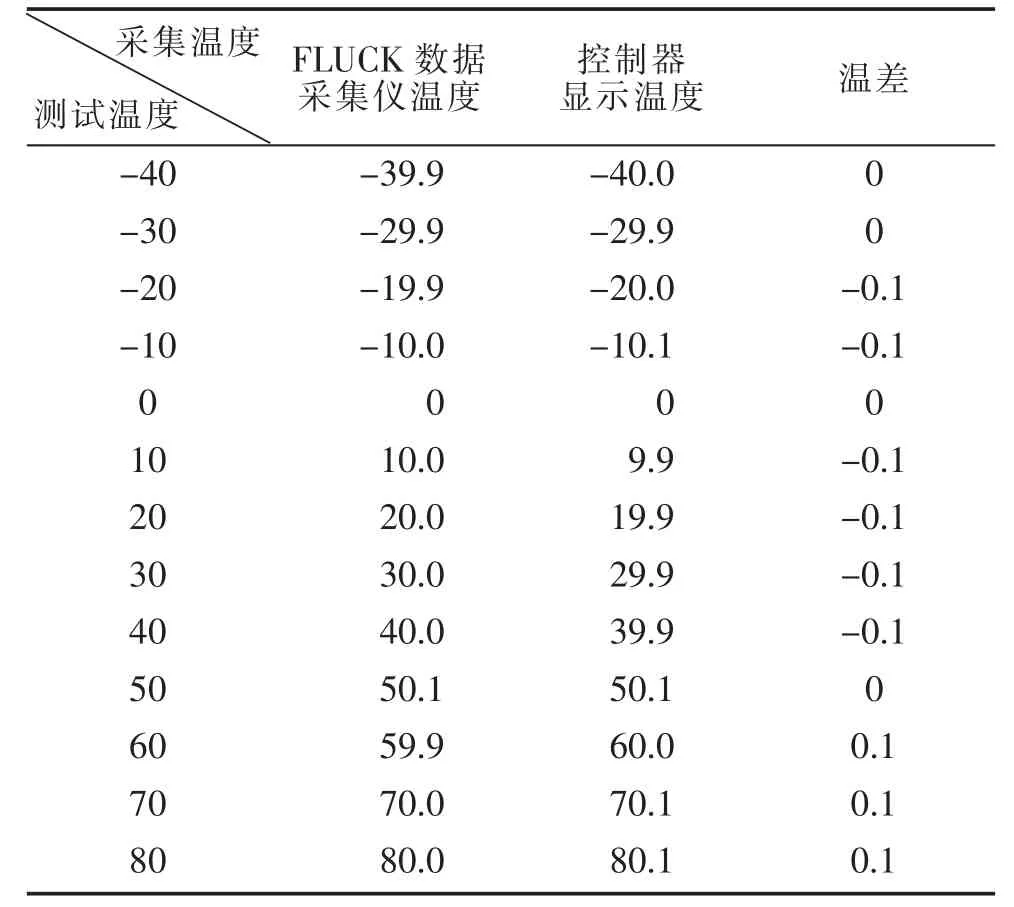
表1 恒温槽测试对比 单位：℃

4 结语

本文基于奈奎斯特定理“过采样和抽取”原理与采用“曲线拟合”计算方式，可以精确、有效地提高MCU中ADC的转换精度，并使得控制器的温度计算精度达到控制器设计需求±0.1℃的精度。其提高ADC转换精度的方法可以应用在其他高精度的控制领域中，具有极大的应用前景，而“曲线拟合”的计算可以扩展至其他非线性控制领域中，提高整体的控制精度。