Fe52T2(T=Cr，Mn，Co，Ni)合金bcc与fcc相结构的第一性原理研究

董 雪，马 爽，武晓霞，那日苏

(1 内蒙古师范大学 物理与电子信息学院，呼和浩特 010022； 2 内蒙古科技大学 理学院，内蒙古 包头 014010)

磁性材料的磁化状态或者磁有序性的电场调控是当前磁学研究的热点之一[1]，在高密度信息存储和电场驱动的自旋电子学器件等领域具有广泛的应用前景。事实上，过渡金属的磁性状态(磁有序性)与其晶体结构密切相关，如金属铁的铁磁相为体心立方bcc结构(称为α相)，而低温面心立方fcc结构(称为γ相)为反铁磁性。Gerhard等[2]在Cu(111) 衬底上生长了2个原子层(monolayer, ML) 的Fe纳米岛(薄膜)，沿垂直衬底方向施加电场时Fe纳米岛从fcc结构转变为bcc结构。通过第一原理计算发现，伴随着Fe纳米岛的结构转变，其磁性从反铁磁态(fcc)转变为铁磁态(bcc)，而这一特性可被应用于电场调控的结构相变存储单元[2-3]，因此针对Fe以及Fe基合金的不同相结构及其磁有序性的研究再次引起人们的重视。而对于类似FeT(2ML)/Cu(111)体系[2]的应用中，基础FeT合金体材料应具有稳定的bcc结构，为此应考虑两点：(1)FeT合金与衬底Cu的晶格失配不应过大，因此掺杂元素T应为原子半径接近于Fe的3d过渡金属，如Cr，Mn，Co，Ni等；(2)FeT合金中的T组分一般应小于10%，因为根据二元合金相图，Mn和Ni在α-Fe中的固相溶解度均小于10%[4]。因此，对Cr，Mn等掺杂的稀释FeT合金的bcc及fcc相结构的稳定性和磁性的研究对具体应用有着重要的现实意义。

目前关于Fe以及FeT基合金的相稳定性以及α-γ相变机制的理论与实验研究较多[5-11]。然而，由于3d过渡金属掺杂的二元FeT合金体系的磁性较为复杂，到目前为止，对合金局域磁矩的理解依然不清楚。Okatov等[12]通过第一原理计算，发现Fe的α-γ结构相变过程中fcc结构的磁性是非共线反铁磁态，而共线的反铁磁态具有最小的能量，但其晶体结构c/a比值约为1.1的fct结构。Mirzoev等[13]通过第一性原理计算，认为在铁磁α-Fe中固溶的Mn原子组分大于3%时，其磁矩与近邻Fe原子的耦合从反铁磁转变为近似铁磁耦合。Glaubitz等[14]通过XMCD技术研究发现，bcc FeNi是铁磁性，合金中Ni的原子磁矩要大于金属Ni的磁矩。然而低温FeNi的相结构研究不全面，根据二元合金相图[4]可以看出Ni很难溶入bcc相结构。另一方面，对低温fcc结构FeNi稀释合金(Ni组分小于10%)磁性的了解较少。Ortiz-chi等[15]研究发现，fcc铁磁性的FeCo合金在Co的组分较小时保持了fcc Fe的高自旋(high spin, HS)和低自旋(low spin，LS)特性，而在FeCo合金中尚未发现反铁磁性的γ相。Wang等[16]通过第一性原理研究了Cr，Ni，Ta和Zr掺杂的γ相Fe70T2合金体系的磁性，发现当体系中产生类似于fcc-hcp相变的晶界时可能出现奇异的磁性转变。本工作采用密度泛函理论研究了稀释掺杂的Fe52T2(T=Cr, Mn, Co, Ni)二元合金bcc和fcc相结构的晶格参数、磁性和相对稳定性，试图发现具有较强磁-结构耦合效应的双稳结构合金。

1 模型与计算

本计算是基于密度泛函理论[17-18]的VASP程序包[19]，在广义梯度近似(generalized gradient approximation, GGA)框架下，采用Perdew-Burke-Ernzerhof(PBE)[20]交换关联势和投影缀加平面波PAW(projector augmented wave)方法[21]。为了保证计算的收敛，平面波截断能选取为500eV，结构优化过程中，原子位置进行完全弛豫，电子自洽计算的能量收敛判据为10-5eV/atom，原子间作用力收敛标准为0.01eV/nm。布里渊区积分的k点取样采用Monkhorst-Pack的撒点方式[22]，bcc相结构k点的网格取为12×12×12，fcc(当c/a≠1，但在其值附近应称fct，为了方便本文用fcc代替)相结构k点网格取为12×12×8。由于Fe具有很好的铁磁性，所以计算中采用了自旋极化的方式，应用Murnaghan方程[23]拟合物态方程。

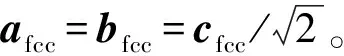
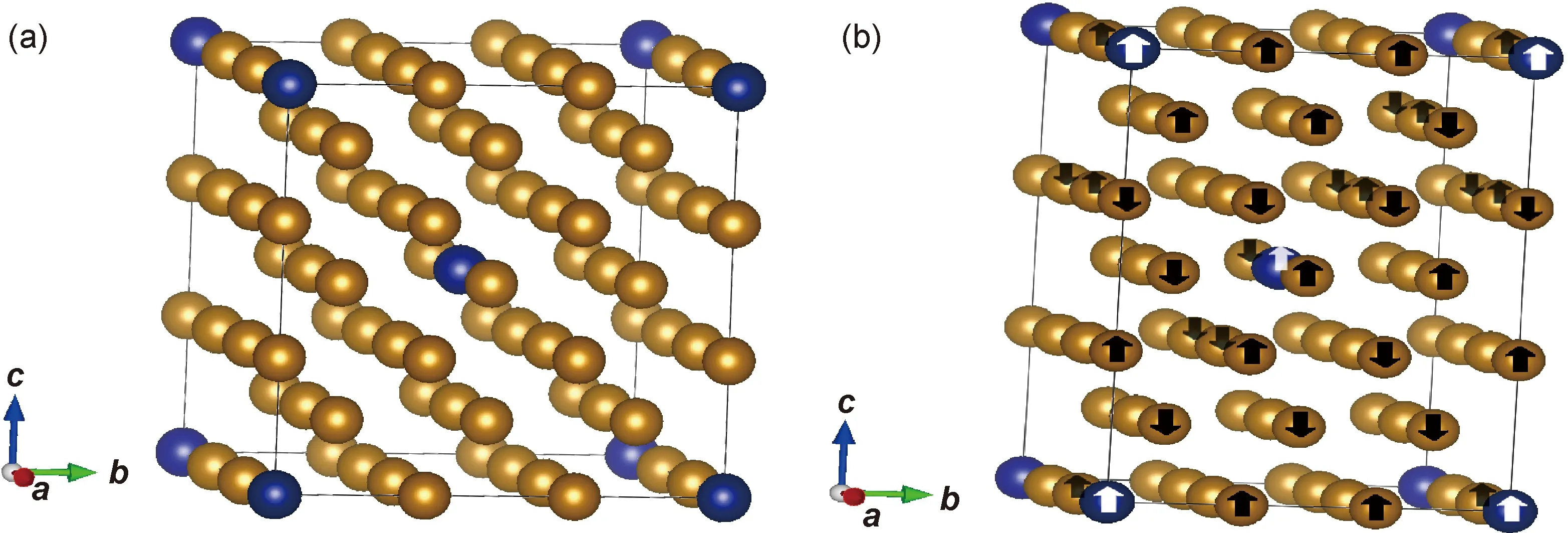
图1 Fe52T2(T=Cr, Mn, Co, Ni)二元合金结构示意图 (a)bcc相；(b)fcc相Fig.1 Structure diagrams of Fe52T2(T=Cr, Mn, Co, Ni) binary alloys (a)bcc phase;(b)fcc phase

2 结果与讨论

2.1 晶格常数与体模量

不同元素掺杂的Fe52T2合金bcc和fcc相结构的平衡态参数如图2所示。图2(a)，(b) 分别给出了Fe52T2合金bcc和fcc相结构晶格常数，图2 (c) 为fcc相的c/a与体积V的关系。从图2(a) 中可以看出，bcc金属Fe的晶格常数a为0.283nm，与实验值(a=0.287nm)相符。由于过渡金属Cr，Mn，Fe，Co和Ni的原子半径非常接近，使得合金的晶格常数变化并不大。其中，FeCr的平衡晶格常数略大于金属Fe的晶格常数，这是因为bcc FeCr固溶体中Cr与Fe反铁磁耦合，而其他3种元素与Fe是铁磁耦合的，因此，Fe52T2(T=Cr,Mn,Co, Ni)合金的晶格常数随着d带电子数增加而略微增大[25]。

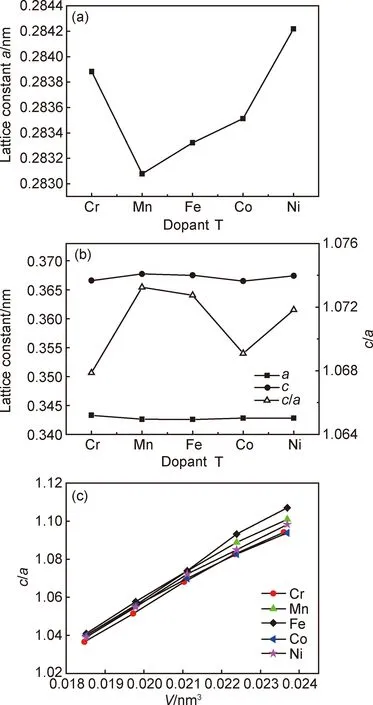
图2 Fe52T2(T=Cr,Mn,Fe,Co,Ni)二元合金平衡态参数(a)bcc相；(b)fcc相；(c)fcc相的c/a与体积V的关系Fig.2 Equilibrium parameters of Fe52T2(T=Cr, Mn,Fe,Co,Ni) binary alloys(a)bcc phase;(b)fcc phase;(c)relationship between c/a and V of the fcc phase

表1中列出了Fe52T2合金bcc和fcc相结构中的原子体积(V)、体模量(B)以及相同组分下bcc相和fcc相每个原子的平均能量差值ΔE(ΔE=Efcc-Ebcc)。可知，bcc相的体积比fcc相的大，说明fcc相的反铁磁性的形成是由于原子间距变小引起的，这符合贝特-斯莱特曲线的预测[26]。由于掺杂浓度较小且过渡金属原子半径与Fe原子的比较接近，所以掺杂后的bcc和fcc相的晶格参数(晶格常数和体积)均变化微小，这使得Fe52T2合金在特定衬底上可能具有与金属Fe类似的bcc和fcc双重稳态和不同的磁有序性。

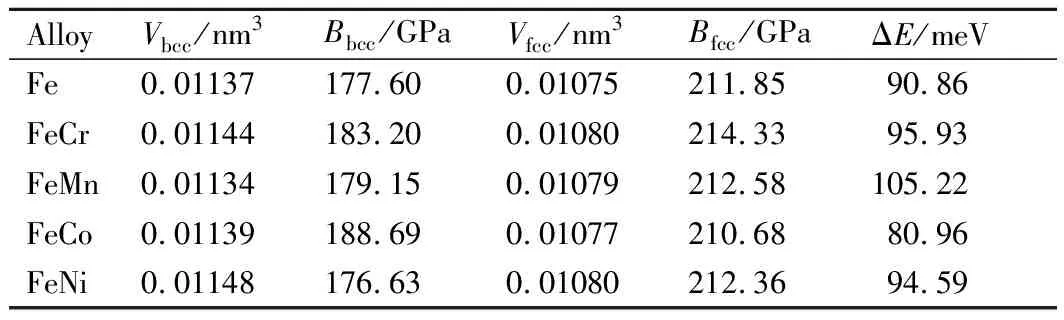
表1 Fe52T2二元合金的bcc相与fcc相原子体积、体模量及bcc相和fcc相平均原子能量差值Table 1 Atomic volume,bulk modulus and average atomic energy difference between bcc and fcc phases of Fe52T2 binary alloys

从Fe52T2合金体模量可以看出，bcc相的体模量约为180GPa，合金化元素的掺入并没有很明显地增加或减小体系的体模量。其中金属Fe的体积和体模量与文献[16]给出的Vbcc=0.01143nm3、Vfcc=0.01030nm3、Bbcc=176.0GPa一致，FeCr和FeNi fcc相的体积也接近文献[16]给出的VFeCr=0.01034nm3、VFeNi=0.01029nm3。按照合金化元素T=Cr，Mn，Co和Ni的变化顺序，虽然体系3d电子逐渐增加，但是体模量的变化并不遵循文献[24]所报道的3d过渡金属体模量的变化规律，说明磁性对FeT合金的成键具有重要的影响[25]。fcc相的体模量随掺杂的变化并不明显，Bfcc约为210GPa。计算得到的fcc相金属Fe的体模量BFe与文献[12]给出的结果比较接近，但是比文献[16]报道的248.7GPa小30GPa。可能的原因是,Wang等[16]的计算是针对严格的反铁磁fcc晶胞模型进行的。两相的体模量相比，fcc相的体模量较bcc相大30GPa左右，这是由于fcc相是密堆排列，原子间距较小所致。

为了研究掺杂合金不同相的相对稳定性，将计算得到的bcc相和fcc相的每个原子平均能量相减，定义了平均能量差值ΔE(ΔE=Efcc-Ebcc)。从表1还可以看到，Fe52T2合金的bcc相和fcc相每个原子的平均能量差值均在90meV附近，与金属Fe的fcc-bcc相的能量差值 90meV[12]吻合得很好，说明计算结果可靠。Fe52T2合金的能量差均大于零，说明在组分约为3.7%的过渡金属掺杂的Fe合金的基态依然是bcc结构。掺杂元素对fcc-bcc能量差ΔE的影响相对较大，约有10%的变化。最小能量差是FeCo合金(ΔE=80.96meV),最大的是FeMn合金(ΔE=105.22meV)。其他合金的能量差值接近于金属Fe的变化，由此说明FeCo合金在bcc相和fcc相的稳定性能相近，而FeMn合金bcc相的稳定性好于fcc相，其他合金在bcc相和fcc相的稳定接近于金属Fe的性质。

2.2 磁性分析

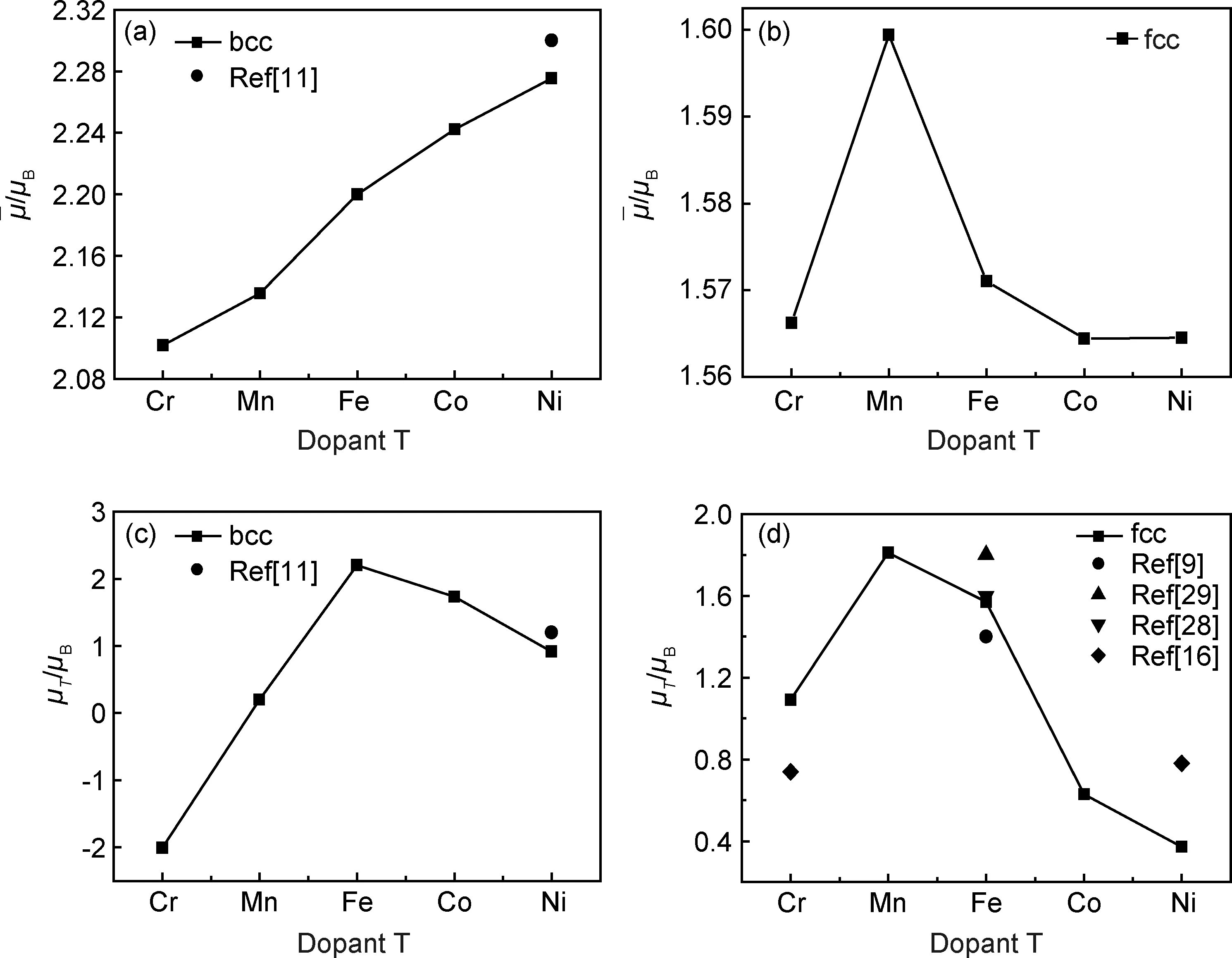
图3 Fe52T2(T=Cr,Mn,Fe,Co,Ni)二元合金的平均原子磁矩(a)bcc相；(b)fcc相；(c)掺杂T的bcc相；(d)掺杂T的fcc相Fig.3 Average atomic magnetic moment of Fe52T2(T=Cr,Mn,Fe,Co,Ni) binary alloy(a)bcc phase;(b)fcc phase;(c)dopant T atoms in bcc phase;(d)dopant T atoms in fcc phase

通过计算，发现掺杂后的Fe52T2合金fcc相的总磁矩也为零，呈现反铁磁状态，所以Fe52T2合金fcc相的平均原子磁矩为同一方向磁化的原子磁矩的平均值，如图3(b)。从图3(b)可以看出，fcc Fe52T2合金中FeMn合金的平均原子磁矩最大，金属Fe次之，然后是FeCr，而FeNi和FeCo几乎相同且较小。从图3(d)可以看出，Cr，Ni原子在掺杂体系中磁矩分别为1.09μB，0.37μB，与Wang等[16]在组分为2.8%时的FeCr，FeNi合金中Cr，Ni磁矩为0.74μB，0.78μB存在差异。通过比较图3(c)和3(d)可知，fcc相中掺杂原子T的磁矩变化与bcc相的明显不同，计算得到的fcc相金属Fe磁矩是1.59μB，与文献中报道的1.4μB[12]，1.6μB[28]，1.8μB[29]相近。对比Fe52T2在bcc和fcc相结构中的金属Fe的磁矩，可以看出金属Fe在fcc相磁矩(1.57μB)小于bcc相的原子磁矩(2.2μB)，FeMn合金fcc相中Mn的原子磁矩为最大1.81μB，远大于其在bcc相的0.20μB。 FeCo和FeNi合金的bcc相中Co和Ni的原子磁矩在bcc相中都大于1μB，在fcc相中都小于1μB且较小，然而FeCr合金中Cr的磁矩绝对值由bcc相中的2μB变成了fcc相中1.1μB。说明在不同结构中由于电子重新分布，产生了较大的局域磁矩变化。

2.3 态密度

Fe52T2合金与金属Fe在bcc相和fcc相的总态密度DOS (density of states)如图4所示。Fe52T2合金与金属Fe在bcc相自旋朝上和自旋朝下的电子分布不对称，均呈现铁磁性；而在fcc相中自旋朝上和自旋朝下的电子分布几乎是完全对称的，总磁矩均为零，呈现为反铁磁性，这与前面自洽计算的磁矩结果是一致的。对比bcc和fcc结构Fe的电子态密度可以看出，bcc结构自旋朝上的子带在费米面以下有明确的DOS峰，分别出现在-1，-2.5eV和-3.5eV处，而自旋朝下的子带在费米面以上约2eV处有一个较高的空态峰。fcc结构的态密度并没有明显的DOS峰，说明态密度在整个能量区间内分布较为平均。图4中bcc相结构在费米面处的总态密度约55eV-1,而fcc相结构在费米面处的总态密度约81eV-1,说明bcc相结构较fcc相结构相对稳定。由于固体结构的稳定性敏感地依赖费米能级附近的电子态的分布[30]，如果体系的费米能级附近存在尖锐的电子态密度峰，则体系将处于高能量的状态而不稳定，而当费米面穿过能隙或赝能隙时，体系较为稳定。对比不同稀释掺杂的Fe52T2合金体系，金属Fe的bcc和fcc相结构的这些特性被保持了下来。

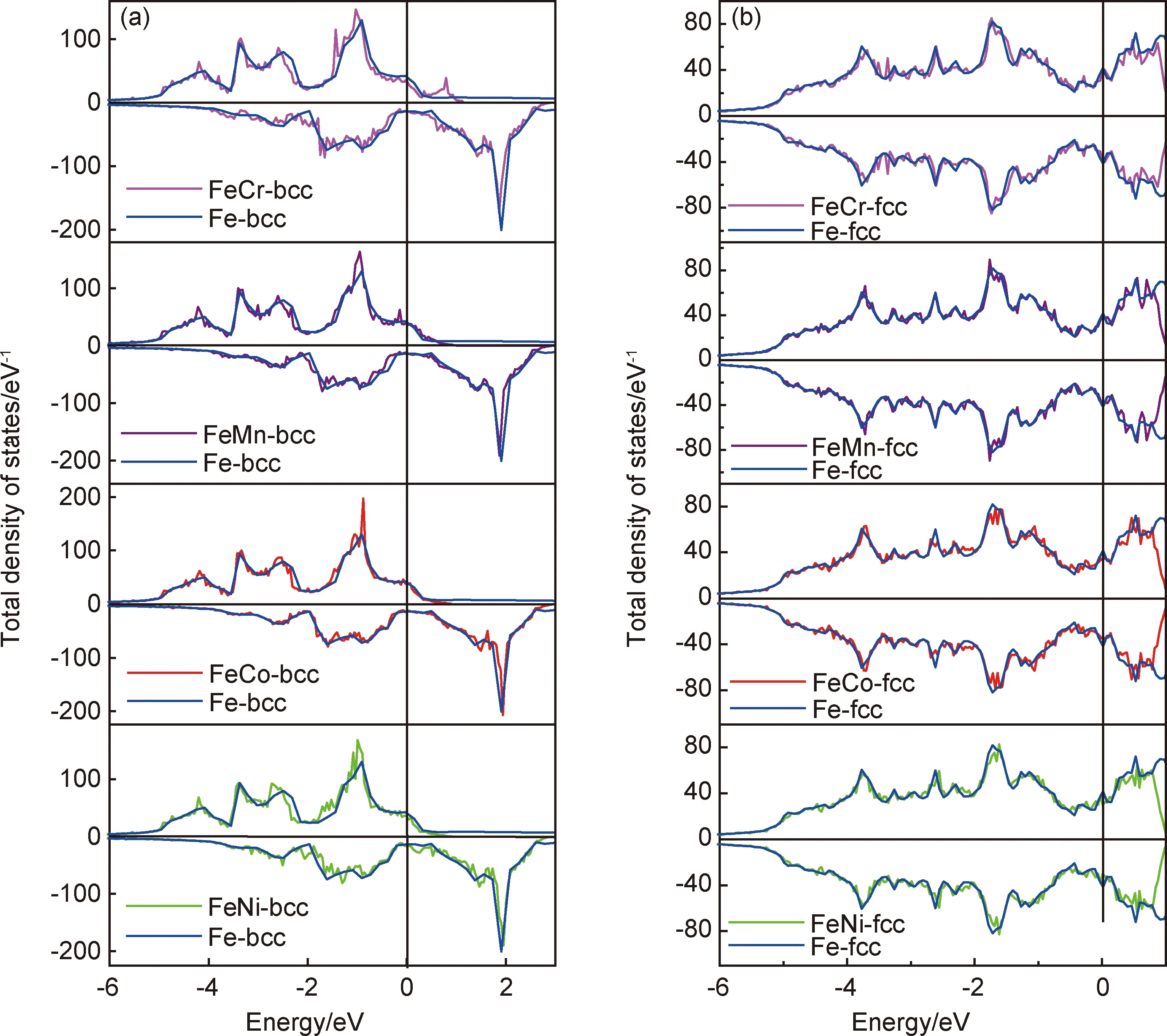
图4 Fe52T2(T=Cr,Mn,Co,Ni)二元合金的总态密度 (a)bcc相；(b)fcc相Fig.4 Total density of states of Fe52T2(T=Cr,Mn,Co,Ni) binary alloys (a)bcc phase;(b)fcc phase

基于以上考虑，图4(a)中给出的4种Fe52T2合金的DOS与bcc Fe的DOS进行了对比，FeCr合金的自旋向上的子带在费米面处的DOS变小，能带向低能方向移动，并且在费米面以上约0.8eV处出现一个空态峰。因此从DOS图像可知，少量的Cr掺杂bcc-Fe52T2体系是稳定的。通过类似的定性分析，还可看出FeNi和FeCo体系依然保持bcc相的稳定性。Mn掺杂的情况有所不同，在费米面附近的DOS变得不光滑，同时在-0.2eV处出现了1个小峰，说明体系可能对晶格形变的相对稳定性影响较弱(与Fe对比)。图4(b)中，fcc相Cr，Mn掺入的合金在费米面处的自旋向上、向下电子态的峰值均与金属Fe相近，说明在fcc相FeCr，FeMn合金体系依然保持fcc相的稳定性(与Fe对比)。Co，Ni掺入的合金在费米面处的自旋向上、向下DOS值低于fcc Fe，尤其是Ni掺杂的合金体系的费米能级被移到DOS谷中，说明Co，Ni的掺杂有助于稳定Fe的反铁磁fcc相结构。

3 结论

(1)Fe52T2(T=Cr，Mn，Co，Ni)在bcc，fcc相结构下的平衡晶格常数a或c和体模量B的变化并不是随掺杂元素d电子的增加单调变化，即不能简单地通过d能带填充图像解释，说明过渡金属T与金属Fe合金化时具有较强的磁-结构耦合效应。

(2)Fe52T2(T=Cr,Mn,Co,Ni) 合金的bcc相和fcc相平均原子能量差值均在90meV附近，说明在组分约为3.7%时，Fe52T2(T=Cr，Mn，Co，Ni)合金的bcc相比fcc相稳定。反铁磁的fcc结构有一定的四方性，面心四方结构(c/a比值约为1.07)的fct相是一个亚稳态。

(3)2种相结构(bcc，fcc)Fe52T2合金中掺杂元素T的磁矩有明显的差别，说明晶格结构的变化引起局域电子重新分布，导致不同磁性相的局域原子磁性改变。