标准表法检定体积管的不确定度评估与分析

谢强

大庆油田工程有限公司

体积管作为对流量计进行在线实流检定应用最广泛的标准器，其测量能力直接关系到油品计量的准确性[1]。测量不确定度用于表征赋予被测量值的分散性。测量过程是否持续受控，测量结果是否能保持稳定一致，测量能力是否符合计量要求，需要用测量不确定度来衡量。测量不确定度越大，表示测量能力越差；反之，则表示测量能力越强[2]。因此，开展对体积管测量不确定度的评估工作是非常必要的。

1 主要流程及操作步骤

在石油工业中，体积管可用于流量计的在线实流检定。检定过程是通过流量计的实际读数值与体积管的标准容积值的比较来完成。目前现场检定体积管的方法主要有容积法和标准表法（标准流量计法）两种[3]。容积法检定需要对体积管进行清洗，不但工程量大而且清洗时间较长。为降低劳动强度，实现体积管的在线检定，标准流量计法开始得到应用[4]。其典型工艺流程见图1。

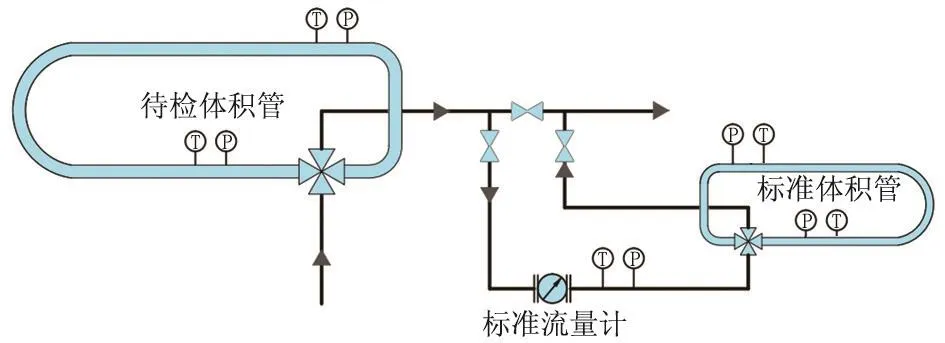
图1 标准流量计法在线检定典型工艺流程Fig.1 Typical process flow chart of online calibration by the standard flow meter methocl

检定过程通常采用以下步骤[3]：

（1）用主标准体积管检定标准流量计，采集相关数据，计算出“初始”标准流量计系数。

（2）用标准流量计检定被检定的体积管，记录标准流量计的累积脉冲数及相关温度与压力数据。

（3）用主标准体积管再次对标准流量计进行检定，得到“结束”流量计系数。

（4）将“初始”流量计系数与“结束”流量计系数进行平均得到检定体积管的过程中标准流量计系数，与步骤（2）中的累积脉冲数等数据结合确定被检体积管的标准容积值。

2 不确定度评估

2.1 数学模型及转化

标准流量计法检定体积管容积示值的数学模型为[3]

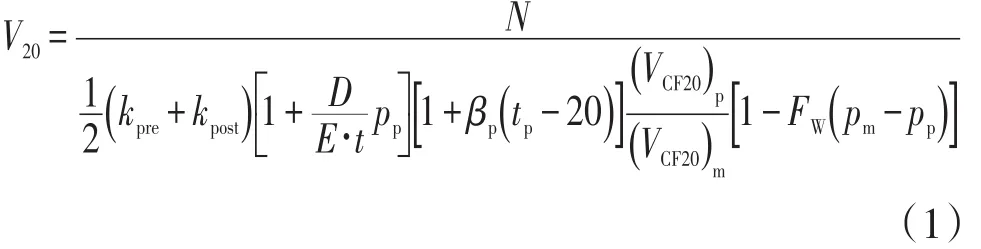
为简化模型进而减少计算量，引入综合修正系数和平均k系数的概念用于模型分析，转化后的数学模型为

式中：k为标准流量计在“初始”和“结束”阶段平均流量计系数，m-3，“初始”与“结束”流量计系数之差不超过0.02%；CCF为综合修正系数，量纲为1；V20为通过标准流量计法得到的体积管容积（20℃，1 bar），m3；N为标准流量计检定体积管得到的脉冲数，量纲为1；(VCF20)p为体积管处的温度下原油的体积修正系数，量纲为1；(VCF20)m为流量计处的温度下原油的体积修正系数，量纲为1；D、t为待检体积管内径及壁厚，mm；E，β为体积管材质弹性模量及钢材膨胀系数，mm；FW为原油和石油产品烃类压缩系数，kPa-1； pm、pp为标准流量计和体积管处的压力，kPa。

2.2 评估各输入量的标准不确定度

2.2.1 k系数的测量不确定度计算

k系数的不确定度分量见表1。

表1 k系数不确定度分量Tab.1 Uncertainty subscale of coefficientk

式（3）中kpre和kpost均采用主标准体积管对传递流量计进行在线检定得到，且kpre和kpost在数量上很接近，会表现出较大的相关性。如果不考虑测量结果分散性的影响，则u(kpre)和u(kpost)各有两个分量：主标准体积管容积示值的标准不确定度ur(V)和各自的重复性标准偏差s[5]。

由于kpre和kpost差异小于0.02%，认为kpre和kpost这两个值是受相同示值误差的影响而同时偏大或偏小了的值，这两个输入量存在正相关，并且相关系数r=±1。由式（3）推导得到，u(kpre) 及u(kpost)的灵敏系数c(kpre)=c(kpost)=0.5。重复性标准偏差sr主要来自检定过程中随机效应，因而不存在相关性，即r=0。

首先将涉及到相关性的分量进行合成，本例中主标准体积管容积示值的不确定度为U(V)=0.42%、k=2，其标准不确定度ur(V)=0.021%。由于上级标准引入的标准不确定度为

在检定过程中“初始”和“结束”阶段流量计系数的复性标准偏差sr分别为0.006和0.004，合成得到的不确定度为

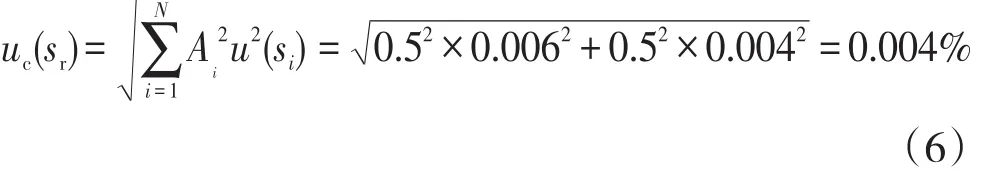
由于以上分量不存在相关性，按均方根合成后得到uc(k)

2.2.2 CCF的测量不确定度计算

CCF不确定度分量见表2[5]。

（1） 内径和壁厚测量的不确定度。本例中待检体积管内径为357 mm，壁厚为10 mm；设用来测量体积管直径与壁厚卡尺的最大误差为±0.02 mm，均匀分布，则ur(D)=ur(t)=1.2×10-2mm，相应的灵敏系数cr(D)、cr(t)为

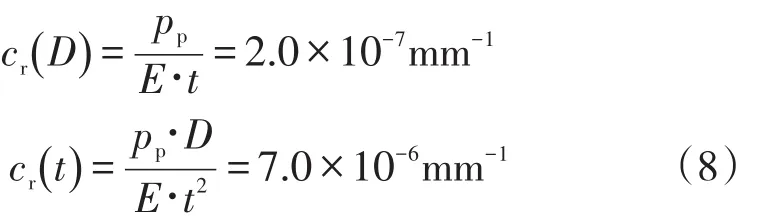
（2） 体积管材质弹性模数的不确定度。材质（钢）的弹性模量为2.06×108kPa，设U(E)=10%，矩形分布，则ur(E)=1.2×107kPa；本例中pp=400 kPa，则灵敏系数为

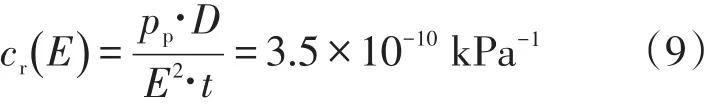
（3） 体积管内压力测量输入的标准不确定度。体积管压力仪表的准确度等级为0.4级，均匀分布，则ur(pp)=0.23%；设压力为400 kPa，ur(pp)=0.92 kPa，灵敏系数为

（4） 体积管与流量计的压力差值测量输入的标准不确定度。流量计使用的压力仪表的准确度等级为0.4级，忽略相关性，均匀分布，ur(pm)=ur(pp)=0.23%；则压力差值的不确定度和灵敏系数为

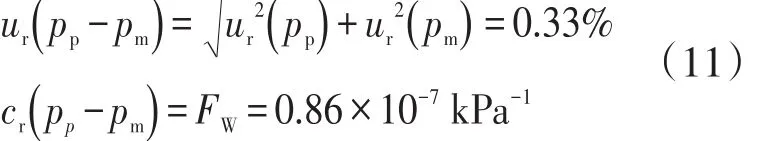
设压力为400kPa，urΔP=ur(pp-pm)=1.32 kPa。

（5） 体积管壁温度测量输入的标准不确定度。温度仪表的最大允许误差为±0.1℃，按均匀分布考虑，则温度测量的标准不确定度为ur(tp)=0.058℃，灵敏系数为

（6） 体积管材质温度膨胀系数输入的标准不确定度。体积管材质温度膨胀系数为33.5×10-6℃-1；不确定度为ur(β)=25%，矩形分布，则ur(βP)=7.2×10-6℃-1，取 tp为50 ℃，则

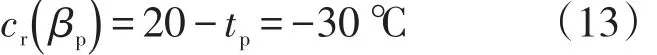
（7） 烃类压缩系数输入的标准不确定度。烃类压缩系数测量不确定度为6.5%，本例考虑到在检定过程可能存在介质的物性变化，设U(Fw)=10%，矩形分布，则ur(Fw)=5.77%。设Fw=0.86×10-7kPa-1，根据文献[5]，则ur(Fw)=5.0×10-9kPa-1；设pp-pm的最大值为400 kPa，压缩系数输入量的灵敏系数为

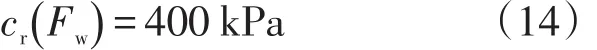
（8） (VCF20)p/(VCF20)m估计值的标准不确定度。根据原油标准密度和温度查《石油计量表》[6]表60-A得到原油体积修正系数VCF20，在检定过程中原油标准密度基本相同，可以近似认为不确定度主要由标准流量计处与体积管处流体温度测量差值引入。设温差为0.2℃，由此引入的估计值最大误差为0.02%，按均匀分布，估计值的相对标准不确定度 ur[(VCF20)P/(VCF20)m]=0.012%， 灵敏 系数

表2 CCF不确定度分量Tab.2 Uncertainty subscale ofCCF

2.2.3 脉冲数的不确定度计算

脉冲数的不确定度分量见表3。

表3 脉冲数不确定度分量Tab.3 Uncertainty subscale of impulse number

（1）标准流量计脉冲的相对标准不确定度[7]。在检定过程中，标准流量计脉冲数至少在10 000以上，允许计数误差为±1个脉冲，其概率分布为均匀分布， ur(N )相对不确定度为0.005 8%，灵敏系数cr(N)=1。

（2）重复性的标准不确定度[8]。重度性的标准不确定度由检定记录给出，重复检定5次，Ei重复性的最大值为0.013%，cr()Ei=1。

2.3 不确定度的合成

考虑到k、CCF、N等各输入量互不相关，根据测量模型合成标准不确定度为[9]

置信概率P＝95%，取k＝2，扩展不确定度为

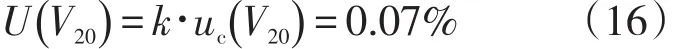
3 结论与建议

（1）标准流量计法检定体积管的测量不确定度要大于容积法，但仍满足0.2级流量计检定要求。

（2）标准流量计法检定体积管不需要对体积管进行严格清洗，比较适用于沙漠缺水地区、海上石油设施等场合。

（3）标准流量计法在检定过程中置换器的运行速度要大于容积法，能够降低动态效应所引起的误差，更加贴近实际操作条件。可以采用此技术对不同流量下体积管检测开关的触发效果的影响开展进一步的研究[10]

（4）在具备相关流程的计量站库中可以采用标准流量计法对体积管的稳定性开展核查工作，其具有操作简单、用时短及更能反映体积管实际状态的优点。