基于图像分解的微电阻率成像测井图像修复方法

陈长胜，袁瑞，王超，张慧敏

(长江大学信息与数学学院，湖北 荆州 434023)

20世纪70年代，为了利用测井资料解决井眼周边地质问题，各大油田技术服务公司推出了高分辨地层倾角测井仪HDT(High-resolution Dipmeter Tool)和地层学高分辨地层倾角测井仪SHDT(Stratigraphy High-resolution Dipmeter Tool)，开启了基于测井技术的井下地质精细研究新领域。80年代，仪器研发人员将地层倾角测井仪的电极板进行了改造，利用密集组合的电阻传感器高密度测量井周地层的电导率，并进行图像处理，得到了高分辨率的地层电阻率图像，最终形成了微电阻率成像测井技术[1]。90年代至今，随着电子元器件的发展，微电阻率成像测井仪器不断完善，电极极板与点击数量逐渐增加[2,3]。目前，Schlumberger公司的全井眼地层微电阻率成像测井仪FMI(Fullbore Formation MicroImager)拥有8个极板，每个极板上24个电极纽扣；Halliburton公司的微电阻率成像测井仪XRMI(Extended-Range MicroImager)拥有6个极板，每个极板上25个电极纽扣[4]。但是，这些极板与电极仍然无法覆盖整个井眼井壁，FMI在8in井眼中的覆盖率为80%；XRMI在8.5in井眼中的覆盖率为67%[5]。测井图像上包含空白区域，呈现出多条相间隔的宽尺度的白色条带、部分数据缺失等特点，严重影响应用效果，不利于地质解释[6]。为了提升图像的应用效果，必须对这些空白条带进行填充，在数字图像处理技术中，填充图像的本质就是图像修复。

图像修复是指对受到损坏的图像进行修复重建或者去除图像中的多余物体，其目的是根据图像现有的信息来自动恢复丢失的信息[7]。该技术广泛应用于文物复原、障碍物移除、影视特效制作、老照片修复、医学图像修复、犯罪现场还原等领域[8,9]。具有代表性的图像修复方法[10,11]包括基于结构的点填充和基于纹理的块填充。偏微分方程(Partial Differential Equation，PDE)修复模型是典型的基于结构的修复方法，包括BSCB模型[12,13]、TV(Total Variation)模型[14,15]、CDD(Curvature-Driven Diffusion)模型[16]等。其中，BSCB模型[12]是由Bertalmio等根据热扩散原理而创立的，该方法的思想是将已知区域信息通过迭代算法逐步传播至未知区域；由Chan提出的TV模型[15,17]是利用已知点的加权平均修复区域边界点，在迭代过程中以各向异性的方式逐步向破损(未知)区域扩散；CDD模型[16,18]是在TV模型上引入几何曲率而得到的驱动扩散模型。然而，基于PDE的修复方法仅适用于小面积破损图像，如图片划痕和少许污点，不能满足大面积受损图像。Criminisi算法[19～21]是使用最为广泛的基于纹理的图像修复方法，其基本思想是按照一定的优先级，在已知区域搜索与未知区域最为匹配的样本块，逐步填充未知区域，该算法能适用于受损面积较大的图像，但在修复过程中会产生较多分布规则的纹理，结构不连续，不符合人眼视觉习惯。文献[6]提及的插值法是一种实现简单、快速的填充空白区域信息的方法，但是忽略了图像的纹理信息。为此，笔者基于数字图像处理技术，针对图像特点，提出了基于反距离加权插值法与Criminisi算法的图像分解的修复方法，利用该方法修复数据缺损的测井图像，并将其与反距离加权插值法和Criminisi算法进行比较分析。

1 反距离加权插值法

反距离加权插值法是一种利用已知散乱点集的多元插值方法。指定插值点的值通过用已知影响点的值加权平均计算得到，其计算公式[6]为：

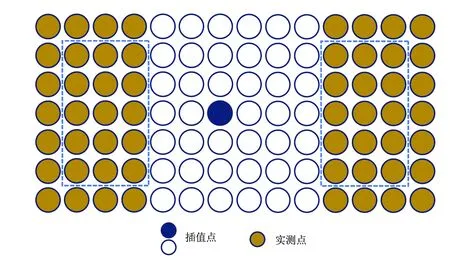
图1 反距离加权插值法示意图

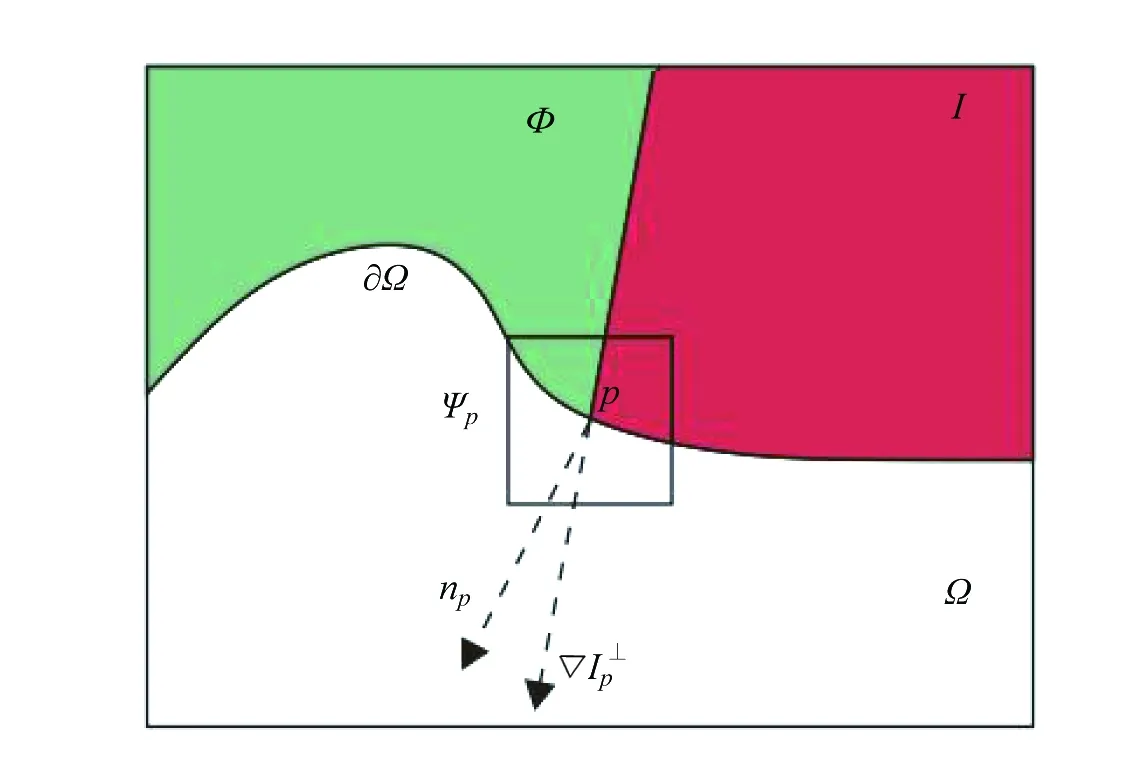
图2 Criminisi算法示意图

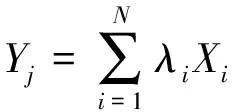
式中：Yj是插值点的值；Xi是影响点的值；N是影响点的总数；λi是对应影响点的权系数；d(i,j)为影响点i与插值点j之间的欧式距离。

反距离加权插值法的示意图如图1所示，在插值点所在行及其上下各2行，每行选取插值区域两侧距离插值点最近的左右各3个实测点，共计30个实测点作为其影响点。在修复过程中，不将已修复点作为后续修复点的影响点。

2 Criminisi算法

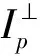
Criminisi算法通过在修复边界选取优先权最大的p点，然后寻找与Ψp最相似的匹配块进行修复，最后更新已修复块中像素点的置信度，该算法通过以下3步实现。

1)计算优先权。Ψp中点p的优先权P(p)[19,20]定义为：

P(p)=C(p)D(p)

式中：C(p)为Ψp的置信度，0≤C(p)≤1；D(p)为数据项，0≤D(p)≤1；Ψp为匹配纹理块中的像素点总数；α为归一化参数，灰度图中取值255。

2)搜索最佳匹配块。最大优先权的点p确定后，在Φ中全局搜索与Ψp相似度最高的匹配块Ψq，Ψq匹配准则[19,21]满足：

式中：d(Ψp,Ψq′)表示Ψp与Ψq′之间的距离。

3)更新置信度。Ψp被填充后，更新填充点的置信度。

重复上述3个步骤，直至未知区域的所有待修复点填充完成。

3 基于反距离加权插值法与Criminisi的图像分解的修复算法

一般而言，一幅图像往往具有丰富的结构信息与纹理信息。图像分解的修复方法[22,23]是由Bertalmio经过长时间地观察研究而提出的图像修复方法，该方法的思想是：首先把原始图像分解成2部分——结构子图与纹理子图，再分别针对性地对2个子图进行修复，最后将修复的子图相加得到最终的修复图像。TV-L1模型[24-26]是一种较好的图像分解模型，它能很好保持图像的结构特征和避免对比度丢失的问题，其模型为：

式中：u和f分别是输出图像和输入图像；前半部分是正则项，是图像的全变分；后半部分是拟合项，用于控制输入与输出间的差异；λ0是拉格朗日乘数。

基于反距离加权插值法与Criminisi算法的图像分解的修复方法的步骤如下：

1)利用反距离加权插值法修复与Ψp的半径相同的图像顶部、底部两处横向的空白区域；

2)利用TV-L1模型分解原始待修复图像，得到结构子图与纹理子图；

3)利用反距离加权插值法修复分解所得的结构子图；

4)利用Criminisi算法修复分解所得的纹理子图；

5)将修复之后的纹理子图与结构子图相加，得到最终的修复图像。

4 试验结果

运用反距离加权插值法、Criminisi算法和基于反距离加权插值法与Criminisi算法的图像分解的修复方法对微电阻率成像测井图像进行修复。图3(a)是一幅缺失65748个像素点的测井图像，该图像的垂向分辨率是2.54mm，横向共356列，其中缺失数据的列数为141列，呈现出多条空白带。该图像显示了砂岩与泥岩地层剖面，亮色代表砂岩，暗色代表泥岩，空白带造成部分岩性特征缺失，影响了沉积构造的识别、岩石结构的分析等地质应用。在Matlab-R2017a平台下，编写相应的程序对图像进行快速处理。

图3(b)是利用反距离加权插值法修复所得的图像，虽然在修复区域视觉效果上较为连续，但在修复区域边界存在较明显的分隔线；图3(c)是利用Criminisi算法修复所得的图像，尽管修复之后的图像纹理较清晰，但是图像结构断裂，整体视觉效果差;图3(d)是基于反距离加权插值法与Criminisi算法的图像分解的修复方法所得的修复图像，该方法不但修复了图像的结构与纹理特征，而且图像连续性好，视觉效果好。

为了客观地说明各方法针对部分数据缺失的测井图像的修复效果，引入如下常用的评价指标[27]。

1)均方误差MSE(Mean Square Error)和峰值信噪比PSNR(Peak Signal-to-Noise Ratio)。它们是以像素统计为基础的图像质量评价方法，计算公式为：

式中：R代表已修复图像；F代表原始待修复图像；MN表示图像大小。

MSE越小，表明修复效果越好，PSNR越大，表明修复质量越佳。

图3 原始图像及修复结果

2)结构相似度SSIM(Structural Similarity)。它是衡量2幅图像相似程度的指标，计算公式为：

SSIM(R,F)=l(R,F)·c(R,F)·s(R,F)

表1 3种方法的修复结果的定量评价

式中：l(R,F)、c(R,F)、s(R,F)分别是亮度、对比度、结构的比较函数；uR、σR分别表示R的均值、标准差；uF、σF分别表示F的均值、标准差；σRF表示R与F的协方差；c1、c2、c3均为常数。

SSIM是根据像素间的相关性构造出来的图像质量评价标准，SSIM越大，表明修复效果越好。

原测井图像的3种修复方法的定量评价指标值见表1，可以看出，基于反距离加权插值法与Criminisi算法的图像分解的修复方法的SSIM值和PSNR值高于反距离加权插值法与Criminisi算法的SSIM值和PSNR值，MSE值低于反距离加权插值法与Criminisi算法的MSE值，表明基于反距离加权插值法与Criminisi算法的图像分解的修复方法的修复效果优于反距离加权插值法与Criminisi算法。

5 结语

针对微电阻率成像测井图像部分数据缺失的特点，提出了基于反距离加权插值法与Criminisi算法的图像分解的修复方法，并将其与反距离加权插值法、Criminisi算法的处理结果进行对比，基于反距离加权插值法与Criminisi算法的图像分解的修复方法具有更优的评价指标值，该方法合理有效地修复了测井图像的结构与纹理特征，修复之后的图像具备较好的连续性和视觉效果，一定程度上扩充了地质信息，可对其加以推广应用。