基于MIKE11的梯级水库群溃决模拟研究
张 杨,柳 滔,伍学文,杨 莹
(三峡大学 水利与环境学院,湖北 宜昌 443002)
1 河流工程概况
河道总长L=110 km,断面形状矩形(B=400 m;h=100 m),断面间距为200 m;上游来水流量Q=20 000 m3/s;底摩擦曼宁系数n=0.02;坡度i=0.9%。其中坝体A的位置在20 km处,坝高80 m;坝体B的位置在40 km处,坝高60 m;坝体C的位置在60 km处,坝高40 m,见图1。
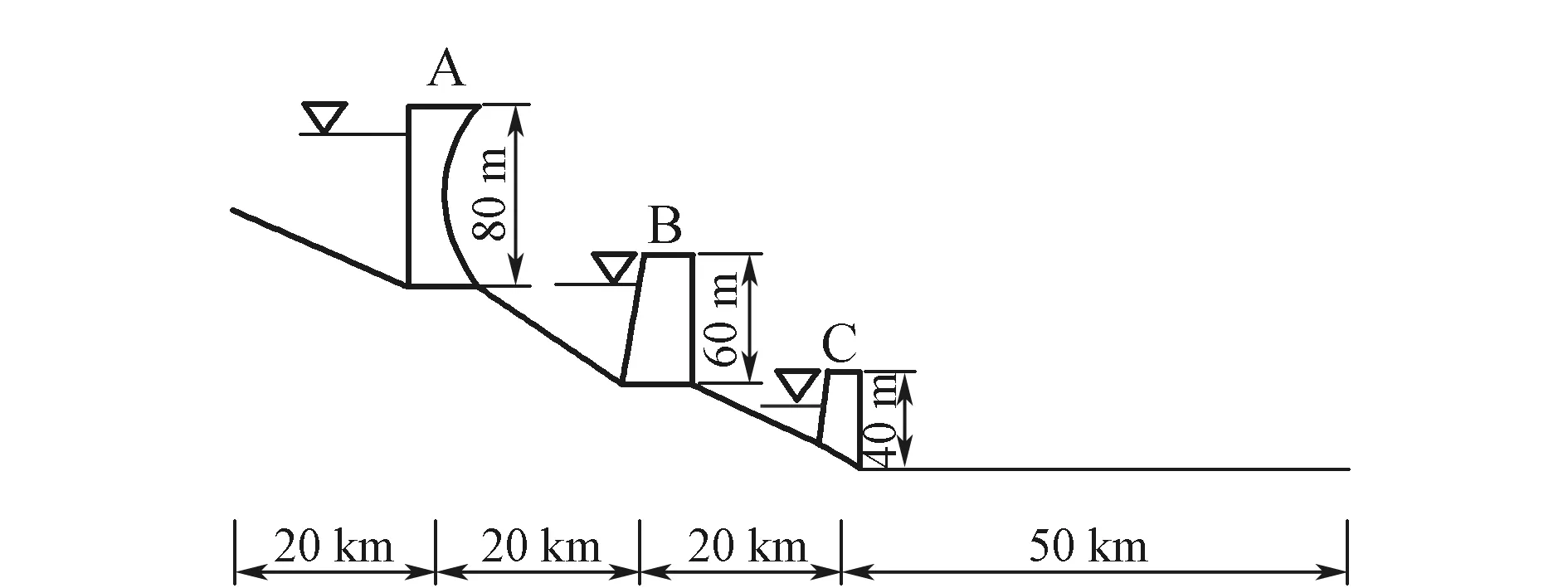
图1 河道纵剖面示意
为了对比单个水库大坝溃决时的洪水演进,本文基于MIKE11模拟了3个梯级水库发生溃决的洪水演进情况,设置了3种工况。
工况1:坝体A发生漫顶溃决,且瞬间一溃到底,坝体全部溃决;坝体B和坝体C漫顶不溃,水流经坝顶溢流。
工况2:坝体A和坝体B发生漫顶溃决,且瞬间一溃到底,坝体全部溃决;坝体C漫顶不溃,水流经坝顶溢流。
工况3:坝体A、坝体B和坝体C全部发生漫顶溃决,且瞬间一溃到底,坝体全部溃决,坝体模拟的溃决历时均为10 min。
2 模型设置
边界条件是上游边界设为20 000 m3/s的流量;为保证下游110 km处为自由出流,将模型河长往下再取40 km,即共150 km,下游边界设为10 m水深。初始条件为水深10 m,流量100 m3/s,河床糙率n=0.02。模拟时间24 h,时间步长为自适应时间。为保证溃坝前,模型的水位保持稳定,选择热启动方式。
3 结果分析
为方便采集溃口的流量与水位随时间的变化数据,本文采用的溃口位置是指坝体下游200 m处的断面位置;为研究洪水沿下游河道的演进规律,取河道下游70 km、80 km、90 km和100 km四处的流量与水位随时间的变化值作为研究。
3.1 工况1
坝体A溃决后,洪水开始向下游第一个水库演进,约16 min后洪水到达坝体B,经坝顶溢流后继续向第二个水库演进,约28 min后洪水到达坝体C,经坝顶溢流后开始向下游河道演进,约35 min后洪水到达下游河道70 km处,如表1所示。
首次将软实力概念引入城市的是中国社会科学院教授倪鹏飞,他对包括城市软实力在内的城市发展和城市竞争做了一系列深入的研究。陈志城等学者把城市软实力界定为“文化软实力、社会软实力和环境软实力之和”。此外还有不少其他学者对城市软实力这一概念进行研究与阐述,最后基本达成共识:城市软实力应该是能够增强城市竞争力的各种因素,比如文化、政策、环境等。
其中,洪峰流量在经过两个水库的消减后由328 328.96 m3/s 减小到159 140.59 m3/s 。而且洪水在经过两个水库时产生了滞留,使得洪峰经过后,水库B和水库C中高于坝体高程的水体继续溢流,产生了后续洪水,从图2中可看出:B坝的流量曲线在下降的过程中较A坝更加平缓,稳定历时也更长,C坝的流量曲线出现了三个峰值,即分别为A坝产生的洪峰、B坝的溢流和C坝自身的溢流。从图4中看出:河道70 km、80 km、90 km处的流量曲线都有两个明显的峰值,而且第二个峰值大于第一个峰值,这是因为A坝产生的洪峰第一次经过时抬高了河道流量,随后B坝和C坝产生的后续洪峰又产生了叠加效应。
同样的,在溃口水位图3与下游洪水演进水位图5中也有类似现象。
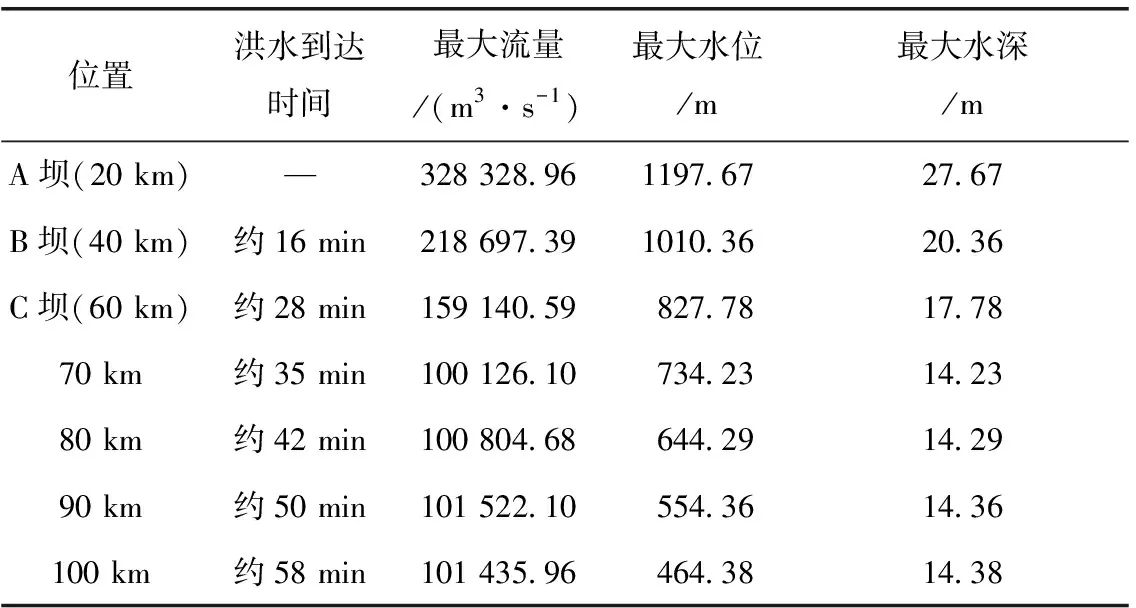
表1 河道流量与水位变化(工况1)
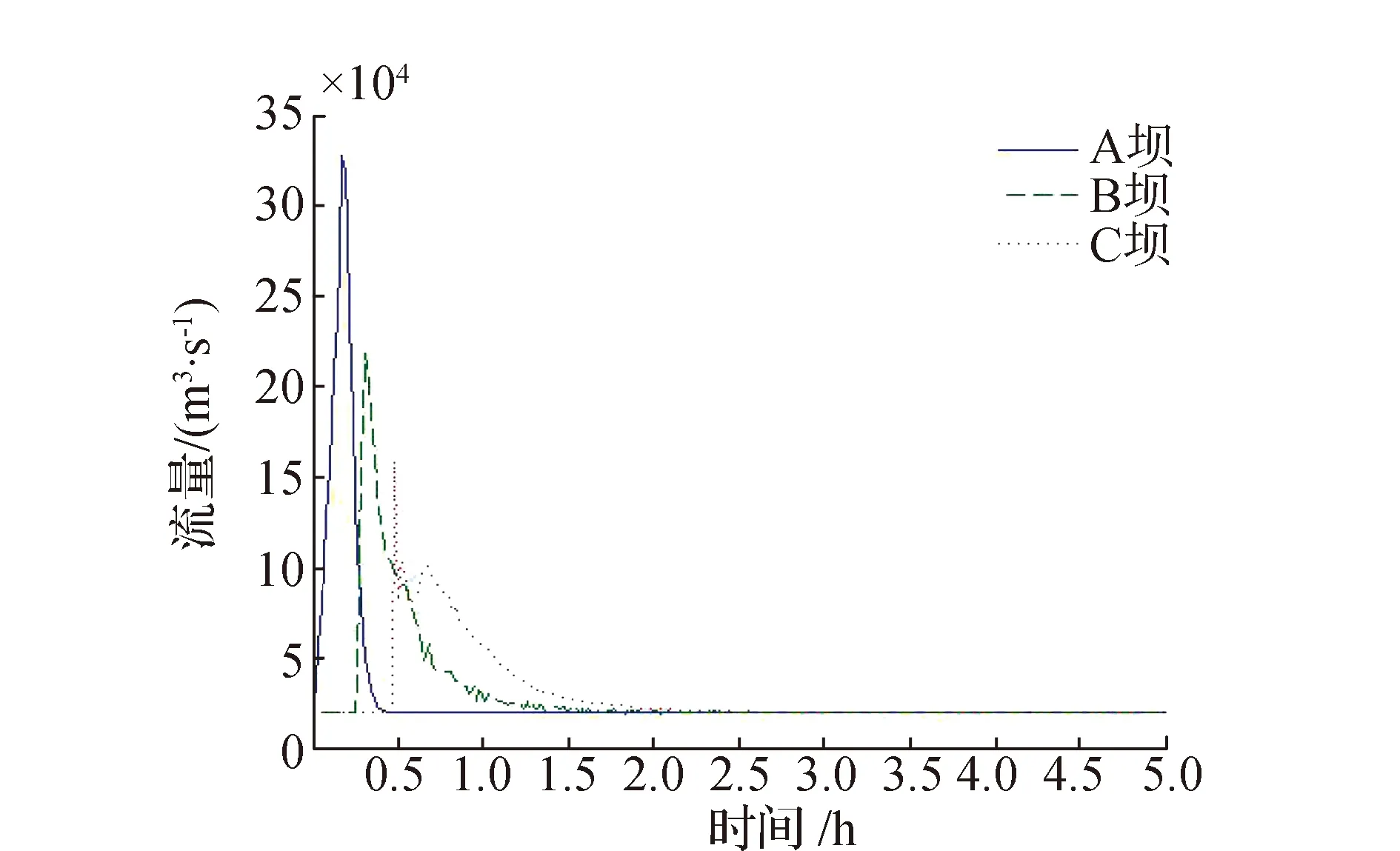
图2 工况1溃口流量图

图3 工况1溃口水位图
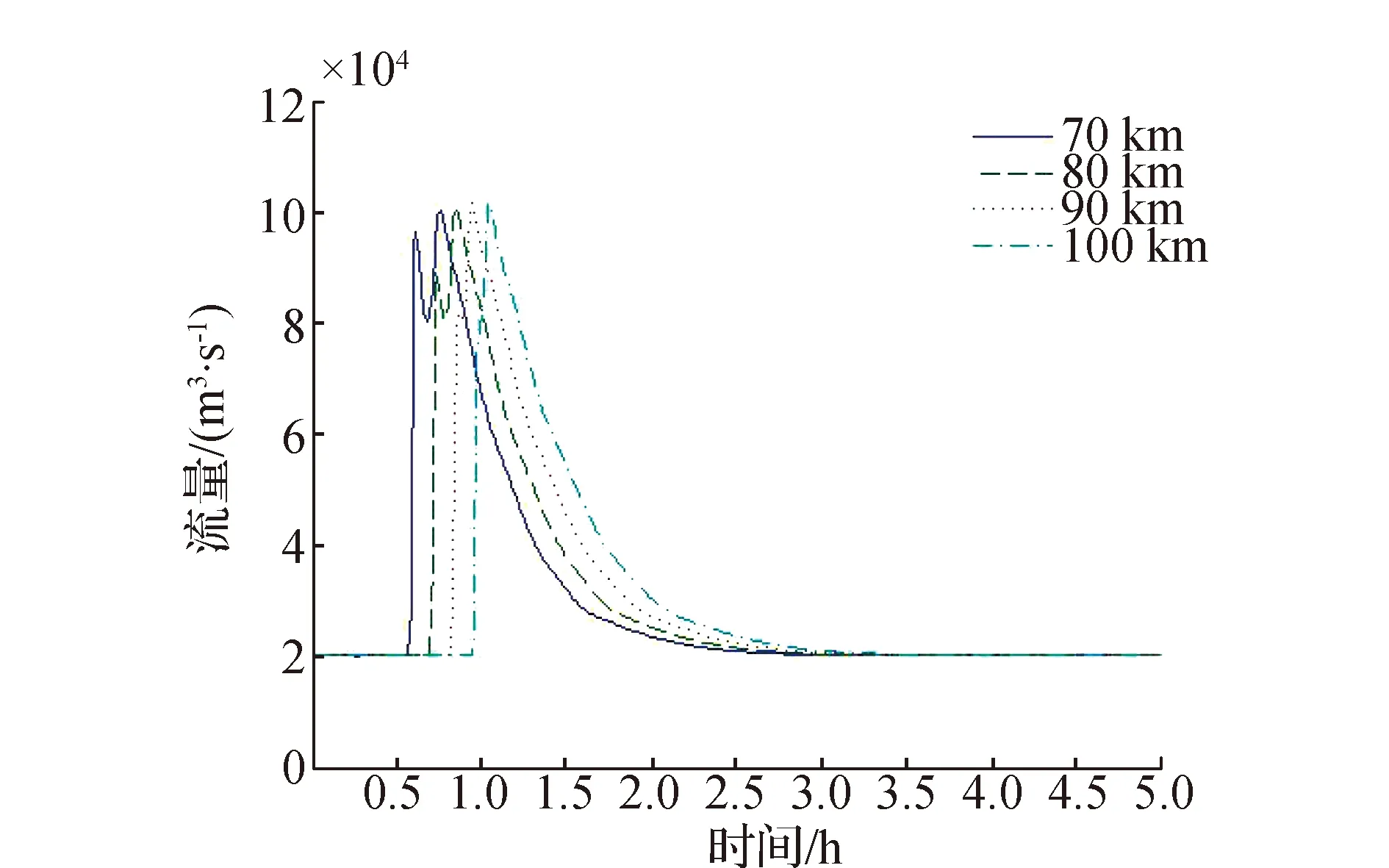
图4 工况1下游河道洪水演进流量图

图5 工况1下游河道洪水演进水位图
3.2 工况2
坝体A与坝体B同时发生溃决,之后A的洪水向B演进,B的洪水向C演进;约16 min后A的洪水到达B,使B处形成第二个流量峰值;C处在约17 min时形成第一个峰值,在约26 min时形成第二个峰值。与工况1相比,工况2的溃口最大流量,除坝体A不变外,坝体B和坝体C至少增加了约6万m3/s,如表2所示。
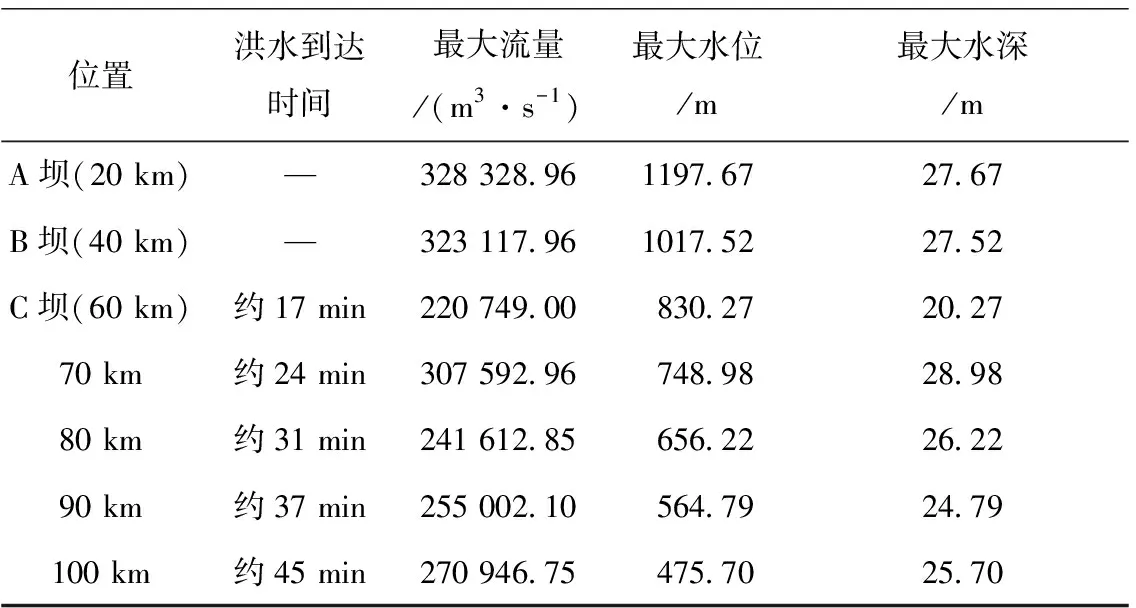
表2 河道流量与水位变化(工况2)
在下游洪水演进过程中也表现出了不同于工况1的变化规律,如图6~图9所示:受坝体A和坝体B洪峰的影响,下游断面最大流量显著增加,最小峰值也为10多万m3/s,最大峰值可达30多万m3/s;同时洪峰在70 km到80 km之间发生了衰减,但从80 km到100 km之间又出现了增强,这可能与坝体A、坝体B的洪峰,以及坝体C的溢流洪峰产生的叠加方式有关。

图6 工况2溃口流量图
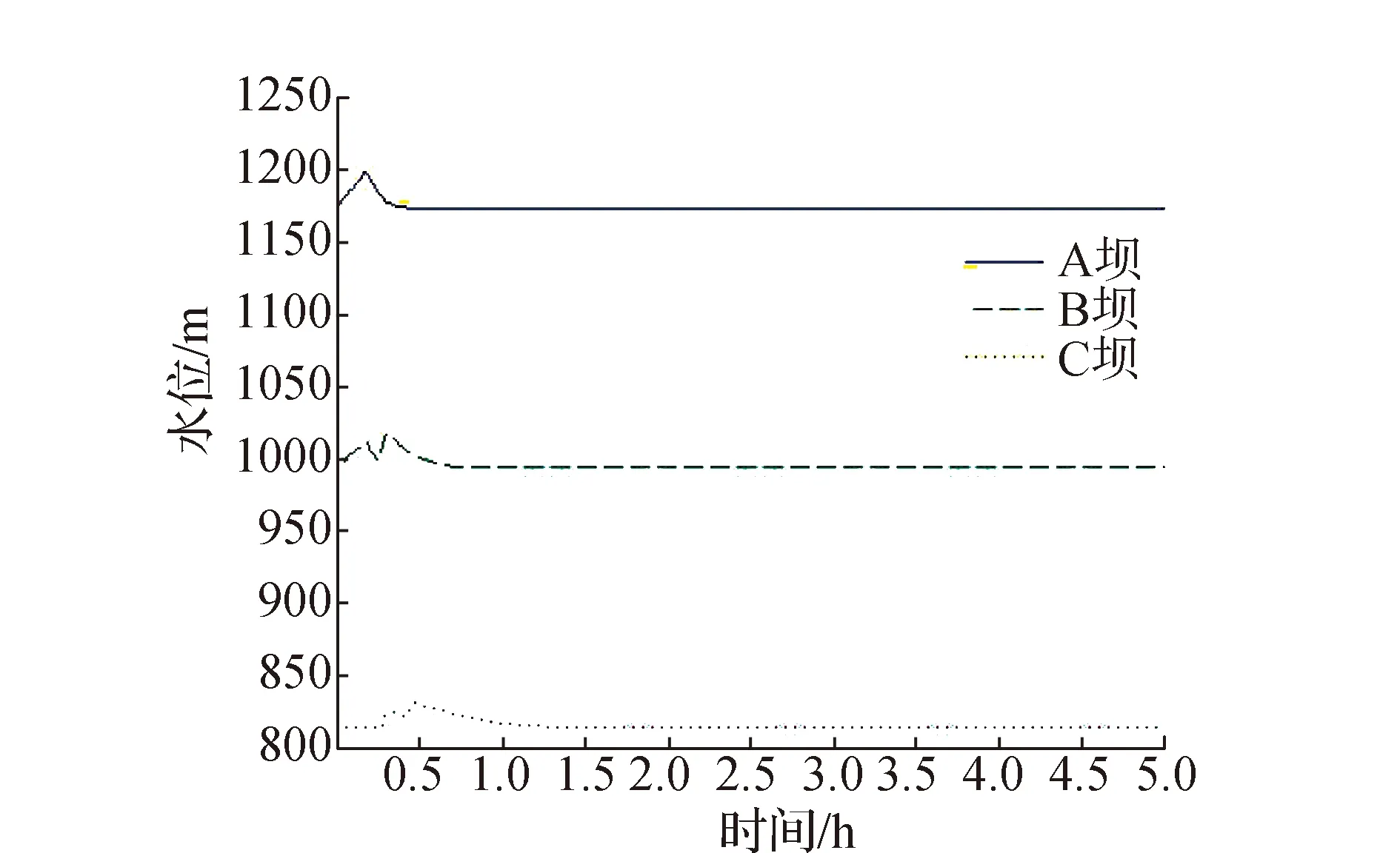
图7 工况2溃口水位图
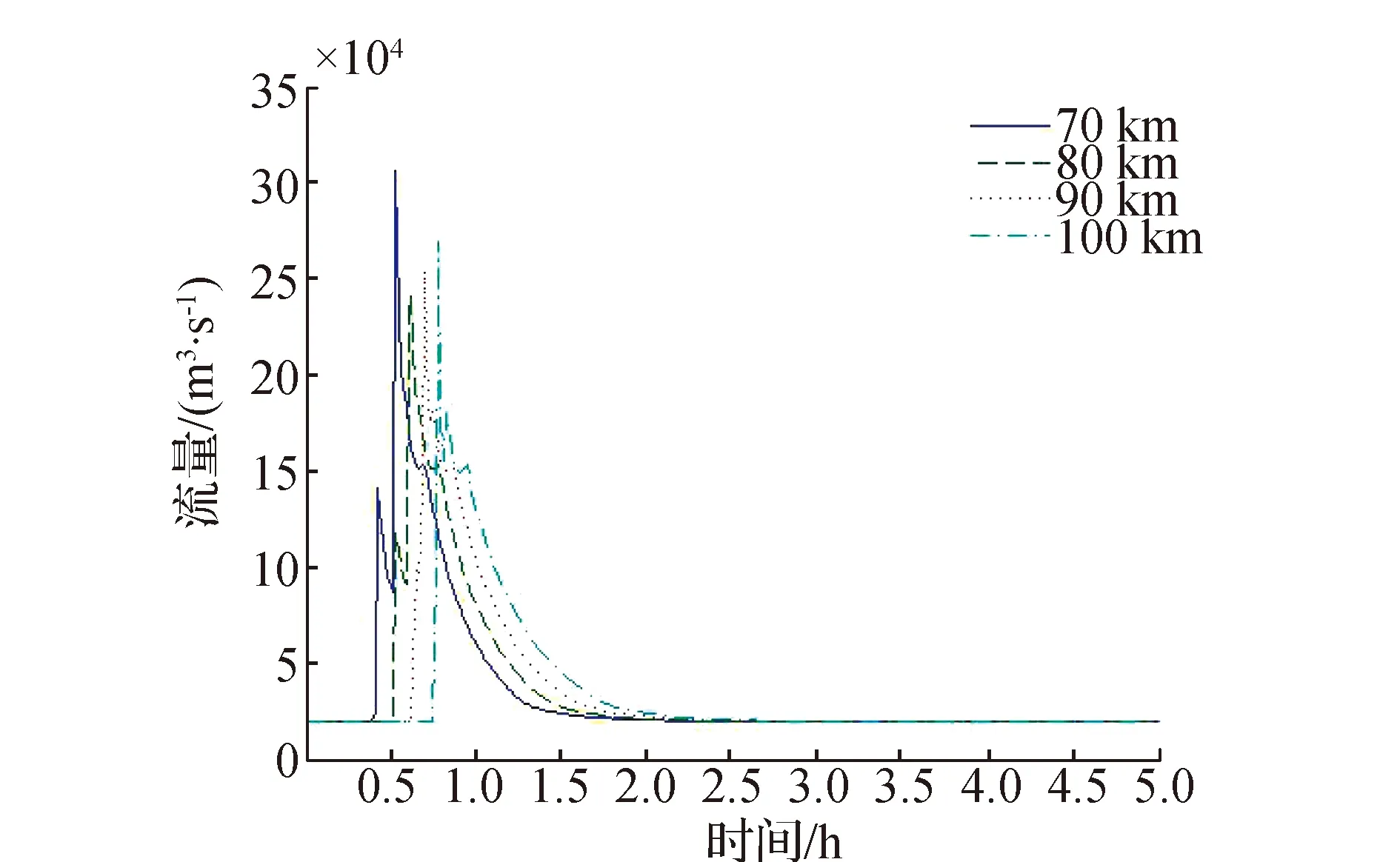
图8 工况2下游河道洪水演进流量图

图9 工况2下游河道洪水演进水位图
3.3 工况3
坝体A、坝体B和坝体C同时发生溃决,从图10~图13中可以看出,坝体A只有自身产生的一个洪峰;坝体B则有自身产生的洪峰和坝体A的洪峰两个洪峰,且坝体A洪峰到达坝体B的时间约为16 min;坝体C则有自身产生的洪峰和坝体A、坝体B的洪峰共三个洪峰,且坝体B洪峰到达坝体C的时间约为18 min,坝体A洪峰到达坝体C的时间约为26 min。由表3可知,坝体A、坝体B和坝体C的最大流量大致相当,都多于32万m3/s。
不同于工况2的是,由于坝体C的溃决导致坝体A、坝体B和坝体C的洪峰在下游发生叠加,使得下游断面的最大流量较溃口流量还要大,最大接近38万m3/s。
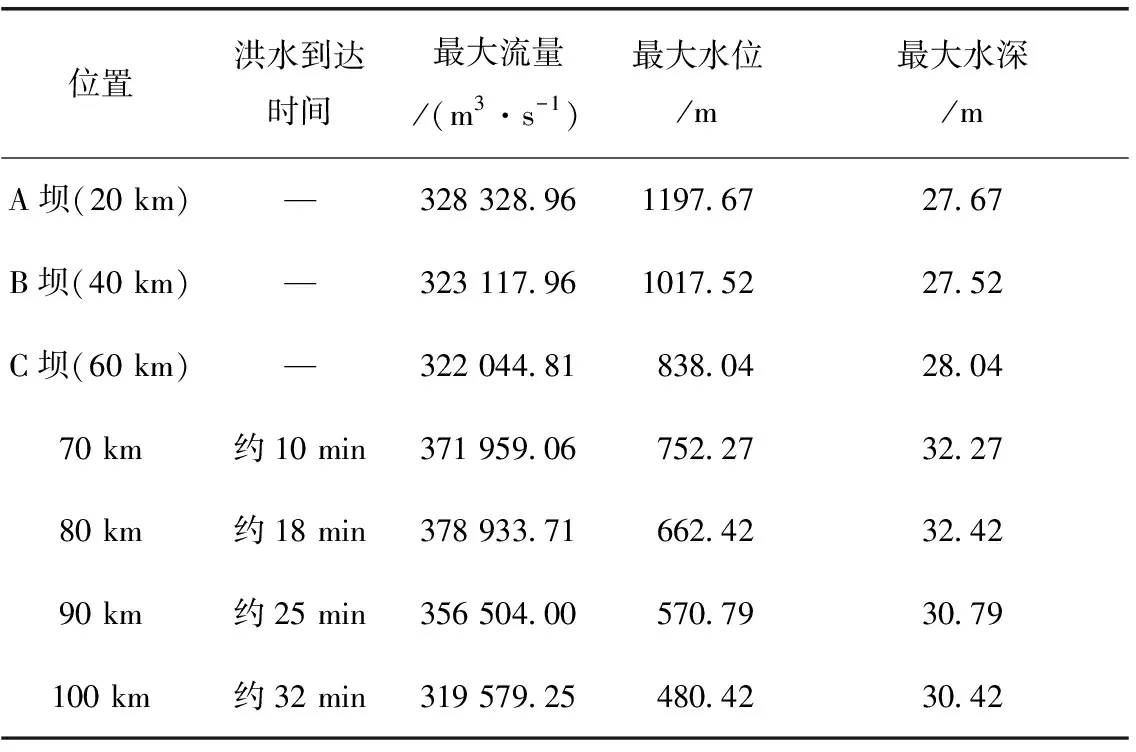
表3 河道流量与水位变化(工况3)
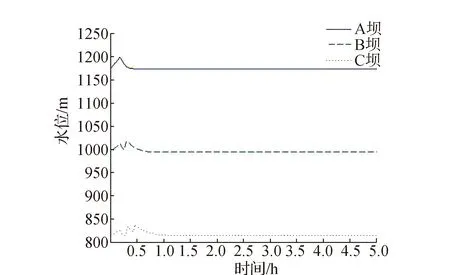
图10 工况3溃口水位图
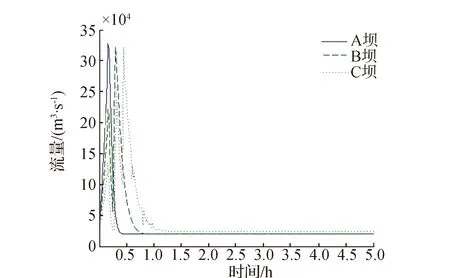
图11 工况3溃口流量图
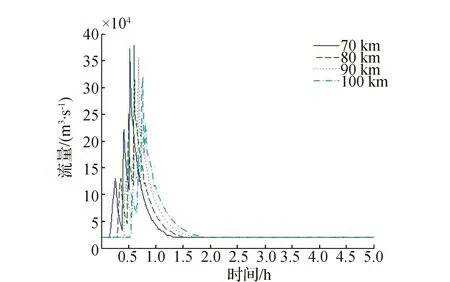
图12 工况3下游河道洪水演进流量图
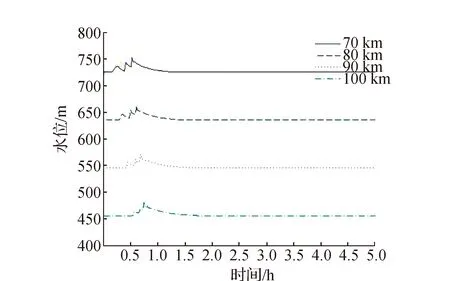
图13 工况3下游河道洪水演进水位图
3.4 对比理论公式
在上述三种工况下溃口流量的计算基于MIKE11的模拟,缺乏理论性推导,为使本文内容更加合理丰富,针对工况1中A坝、工况2中B坝、工况3中C坝的最大溃口流量运用目前主要4种常用的经验公式[7]来进行分析:
(1)圣维南:
(1)
(2)黄河水利委员会:
Qm=0.296g0.5(B/b)0.4
[(11H0-10h)/H0]0.3bh1.5
(2)
(3)铁道部:
Qm=0.27g1/2(L/B)1/10(B/b)1/3b(H0-kh′)3/2
(3)
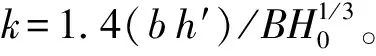
(4)肖克利契:
(4)
式中:Qm为溃口流量,m3/s;b为溃口平均宽度,m;H0为溃坝前上游水深,m;L为库区长度,m;B为大坝坝长,m;h′为溃坝最终残留高度,m;h为有效水深,m;k为经验系数。
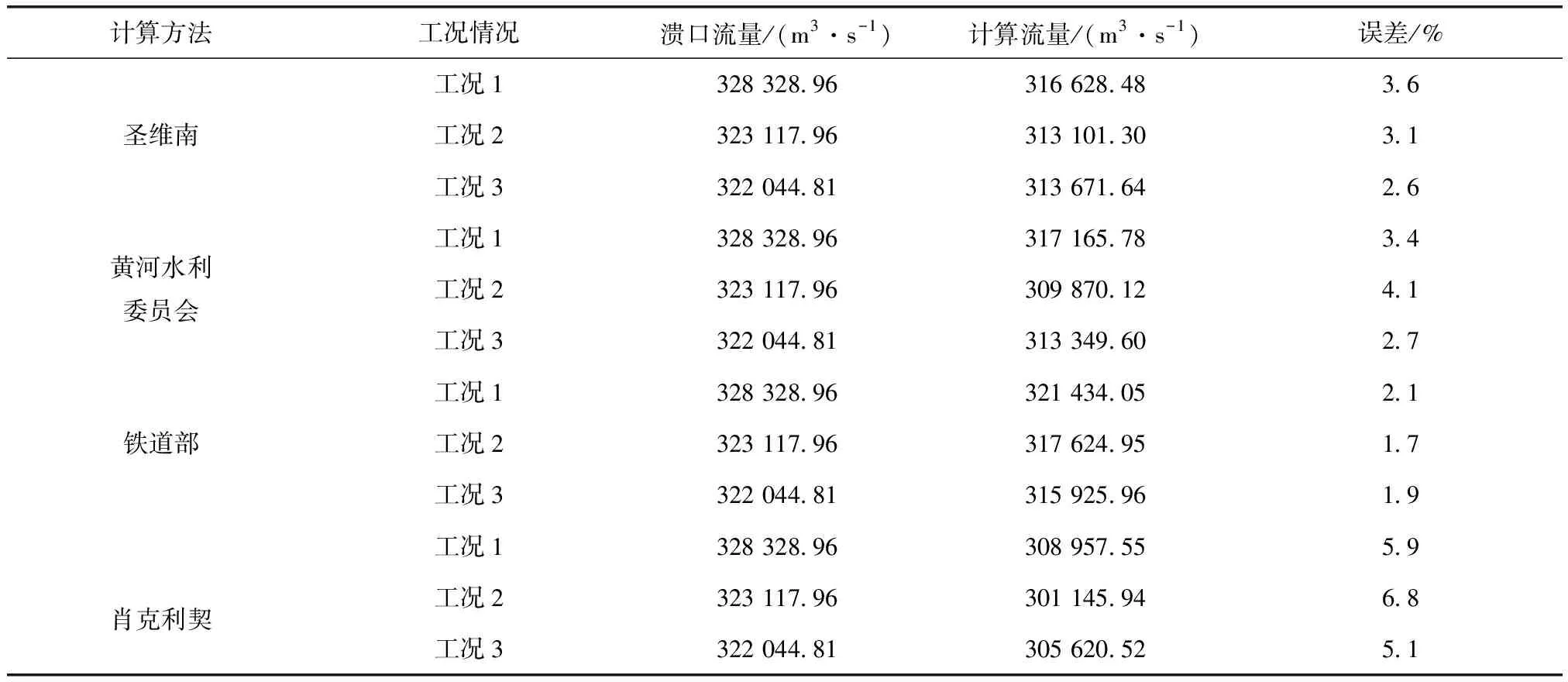
表4 不同工况条件下的4种理论公式计算流量表
由表4可知:对比4种经验公式的计算流量结果,均要小于MIKE11的溃口流量模拟值,且误差范围大概在1.7%~6.8%之间;相对于其他三种理论公式而言,铁道部给出的理论公式计算结果误差最小,与MIKE11的模拟情况较为吻合。
4 结 论
(1)相对于单坝溃决来说,在梯级水库中只溃1级的情况下,下游河道的洪峰在一定距离内没有出现衰减,如工况1中下游70~100 km的河道洪峰流量都保持在大于10 万m3/s。
(2)在发生梯级溃坝时,随着溃坝数的增加,下游河道的洪峰流量也会增加,甚至超过溃口的最大流量,如工况3中下游河道流量超过溃口近5万m3/s,其危害性远远大于单个水库坝体溃决。
(3)4种经验公式计算下的计算流量,都要小于溃口流量数学模拟分析值,且误差范围大概在2%~7%;相对于其他三种理论公式而言,铁道部给出的理论公式计算结果误差范围最小,与数学模拟分析情况较为吻合,更适用于实际大坝溃口流量的理论计算分析。

