圆形管桩上波流力不同计算方法对比研究

赵多苍

（中国铁建大桥工程局集团有限公司 天津 300300）

1 前言

海洋是一个巨大的资源宝库，随着社会的发展、科技的进步，人类对海洋的开发力度也在不断加大，海岸及近海修建了各种海工建筑物。桩基结构已广泛地应用于跨海大桥、钻井平台等海洋工程中。在这些海洋工程设计中，桩基结构所承受的波浪荷载通常是结构设计的控制荷载。因此，准确确定波浪力对海洋工程的设计施工具有重要意义。

对于桩基结构上的波浪力，按照其桩径是否对波浪运动有显著影响，分为与波浪特征长度相比较小和较大两类来考虑［1］。对于相对尺度较小的结构物（构件直径D/波长L＜0.2时），计算主要采用基于圆柱绕流的Morison公式。Morison公式认为当构件直径相对很小时，波浪场基本上不受桩柱存在的影响而传播［2-3］。这时桩柱所受波浪力由两部分组成，一部分是由于水体粘性影响而产生的粘性力；另一部分是由于流体的惯性及桩柱的存在而产生的惯性力。对于相对尺度较大的结构物（构件直径D/波长L＞0.2时），其存在对波流场的影响不可忽略，计算也较为复杂［4］。本文主要对小尺度圆形直立桩柱的波浪力展开分析。

2 桩柱上波浪力分析

设有一圆柱体，直立在水深d的海底上，波高为H的入射波沿x正方向传播，柱体中心轴线与未扰水面的交点为坐标轴的原点，z轴垂直向上。波浪力计算简图见图1。

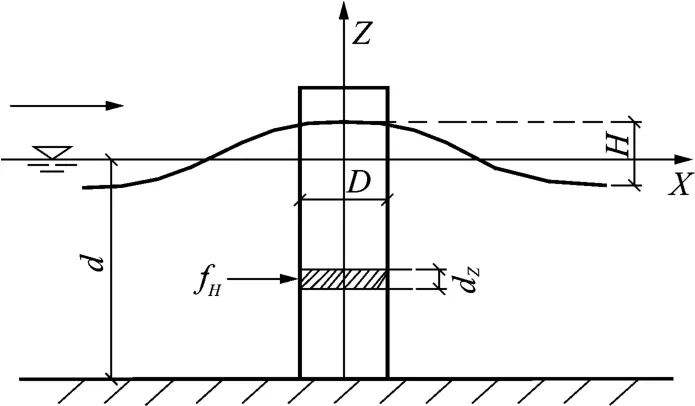
图1 圆形桩柱波浪力计算简图

Morison公式认为作用于柱体任意高度z处的水平波浪力包括两项：水平拖曳力和惯性力［5］。整个柱体上的水平波浪力：

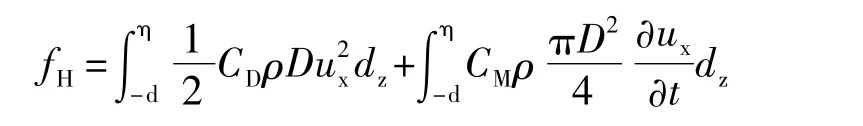
式中，CD、CM分别为阻力系数和惯性力系数；d为水深；D为管桩直径；H为波高；ρ为水密度。

Morison公式中的ux，随选用的波浪理论不同而异。因此，计算作用在直立柱体上的水平波浪力的关键问题是针对柱体所在海域的水深和设计波的波高、周期、水深等条件选用一种合适的波浪理论来计算波浪的ux。同时合理选取阻力系数CD和惯性力系数

合理确定Morison公式所含的拖曳力系数CD和惯性力系数CM是一个重要的研究课题。国内外学者［7-9］对此开展了大量的研究工作，给出了CD和CM的建议值。表1总结了国内外若干规范建议的CD及 CM的值［10］。

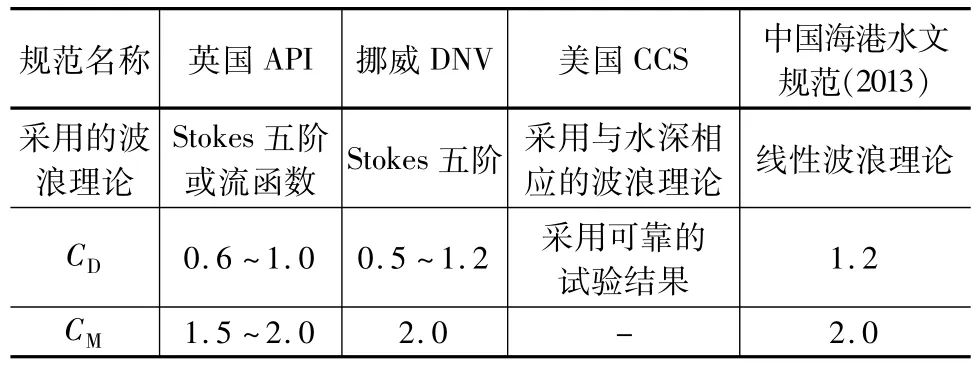
表1 国内外拖曳力系数及惯性力系数取值

3 工程应用

新建福平铁路平潭海峡公铁两用大桥为国内首座公铁两用跨海桥梁。其中，大桥跨越大练岛至平潭岛北东口水道为全线的控制性工程之一。桥址处为典型的海洋性气候特征，台风频繁、潮差大、浪高、流速急。北东口水道特大桥采用高桩承台基础。为方便主体结构施工，采用搭设钢管桩栈桥（管径1.4 m）、独立钻孔施工平台（管径3.3 m）等辅助措施。现利用Morison公式理论计算和三维数值模拟方法，研究不同工况下施工辅助临时结构的钢护筒及栈桥的钢管桩上承受的波浪荷载［11-12］。

3.1 数值模型

利用流体计算软件建立三维数值模型，模拟波浪、海流与钢管桩的相互作用，模型如图2所示。模型前端为波流耦合边界，末端为出流（Outflow）边界，底面设为无滑移壁面（No-slip Wall）边界；其余各面均设为对称（Symmetry）边界，并在末端设置海绵层消波（Wave absorbing），消除反射波对结构物的影响。

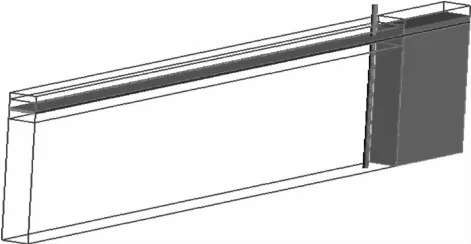
图2 三维数值模型

3.2 计算工况

为分析不同参数作用下钢管桩上波流荷载的变化规律，根据工程所处的海洋环境参数和现场管桩参数，选择46组工况进行研究。各工况参数见表2。

3.3 结果分析

为了将计算值与模拟结果进行对比，波流力计算选择英国API规范Stokes五阶波理论和线性波理论计算。其中，Stokes五阶波计算时，拖曳力系数CD和惯性力系数CM分别取0.8、1.7。

（1）不同波高工况下计算值与模拟值对比

图3～图4是不同浪高工况下，钢护筒、钢管桩上波流力模拟值与计算值对比曲线。从图中可看出，随着波高的增大，管桩上的波浪荷载也随之增大。在4.65 m波高工况下，计算得到的最大波浪力为578 kN，模拟结果为513 kN。波浪力对比结果发现，模拟值跟Stokes五阶波理论计算值相近，在波高较小时，二者之间近似相等，但线性波理论计算值结果较模拟值大。

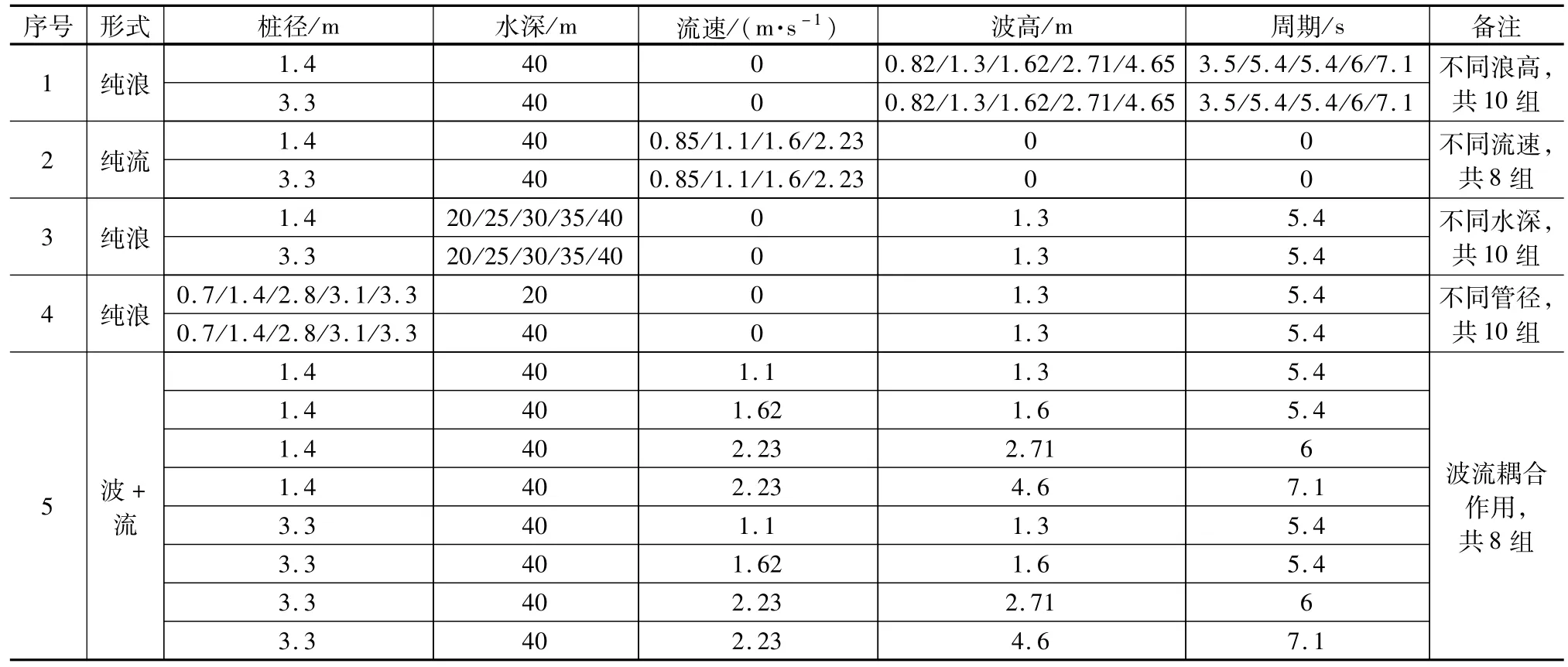
表2 各计算工况相关参数

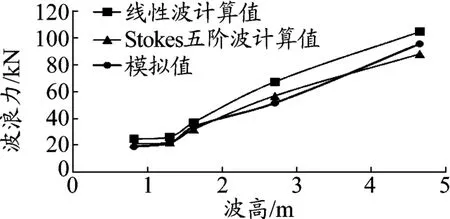
图3 栈桥钢管桩波浪力随波高的变化曲线

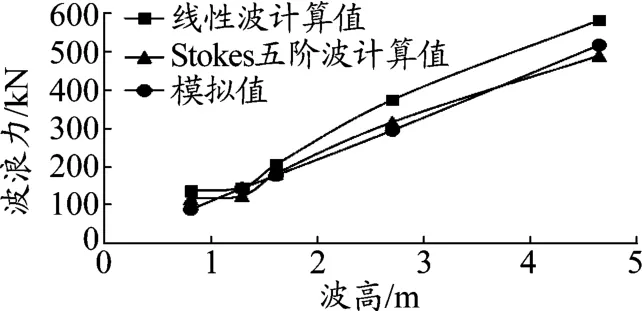
图4 平台钢护筒波浪力随波高的变化曲线

（2）不同水深工况下计算值与模拟值对比

图5～图6是不同水深条件工况下，钢护筒、钢管桩上波流力模拟值与计算值对比曲线。从图中可看到随着水深的增大，管桩上的波浪荷载也随之增大，但增加幅度不大。说明在纯波浪作用下，水深对波浪力的影响不大。这是因为波浪的能量80%主要集中在水面附近，随着水深的增加，波浪在深度方向的影响极剧减弱，波浪荷载也相应减小。在40 m水深下，计算得到的最大波浪力为143 kN，模拟结果为122 kN波浪力。对比实测值和计算值可知，模拟结果跟Stokes五阶波理论计算值相近。

图5 栈桥钢管桩波浪力随水深的变化曲线

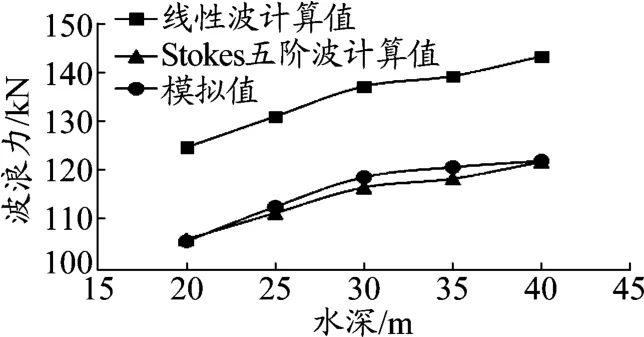
图6 平台钢护筒波浪力随水深的变化曲线

（3）不同管径工况下计算值与模拟值对比

图7为不同管径工况下，管桩上波流力模拟值与计算值对比曲线。从图中可发现随着管径的增大，管桩上的波浪荷载也随之增大，且幅度变化较大。

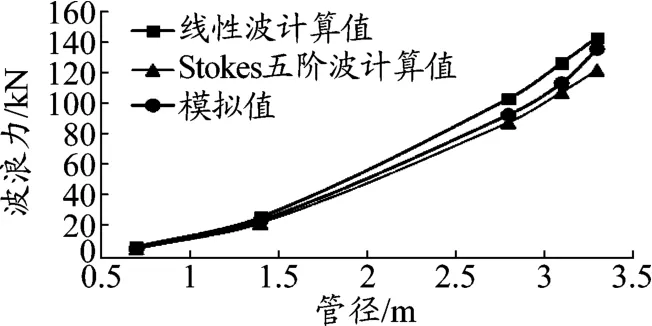
图7 40 m水深时桩波浪力随管径的变化曲线

对比模拟值与理论值可知，管径较小时，Stokes五阶波、线性波计算值与模拟值近似一致；随着管径的增大，线性波计算值较另外两数值大。

（4）纯流作用工况下计算值与模拟值对比

图8～图9是不同流速工况下，管桩上水流力模拟值与计算值对比曲线。可以看出，随着流速的增大，管桩上的水流荷载也相应增大，且增幅较大，说明流速对水流力的影响较大。在40 m水深下，3.3 m钢护筒上计算得到的最大水流力为532 kN，模拟结果为479 kN。对比实测值和计算值可知，流速较小时，模拟结果跟理论计算值吻合性较好，但随着流速的增大，差异稍有增加。

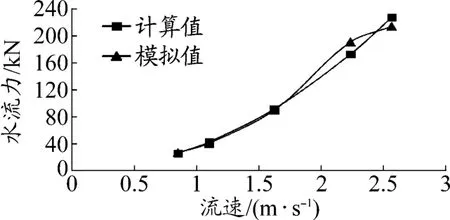
图8 栈桥钢管桩水流力随流速的变化曲线

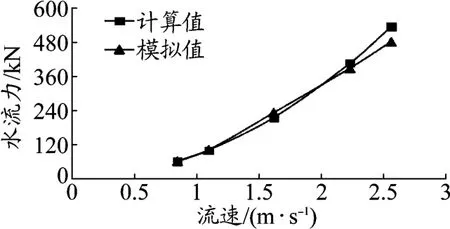
图9 平台钢护筒水流力随流速的变化曲线

（5）波流耦合工况下计算值与模拟值对比

不同波高、水流工况下，管桩上波流荷载模拟值与计算值见表3。分析表中数据可知，随着波高、流速的增大，管桩上的波流力也随之增大。

通过对比发现，线性波理论计算值在4.65 m波高条件下波浪力为578 kN，2.23 m/s流速条件下水流力为403 kN，波流共同作用下波流荷载为976 kN；Stokes五阶波理论计算值4.65 m波高条件下波浪力486 kN，2.23 m/s流速条件下水流力为403 kN，波流共同作用下波流荷载为889 kN。可以看出，波浪荷载近似等于波浪力＋水流力。但计算忽略了波浪和水流的相互作用，跟实际情况存在较大差异。模拟结果波浪力为513 kN，水流力为386 kN，波流力为926 kN。说明数值模拟结果考虑波流耦合作用时，得到的波浪荷载更符合实际情况。

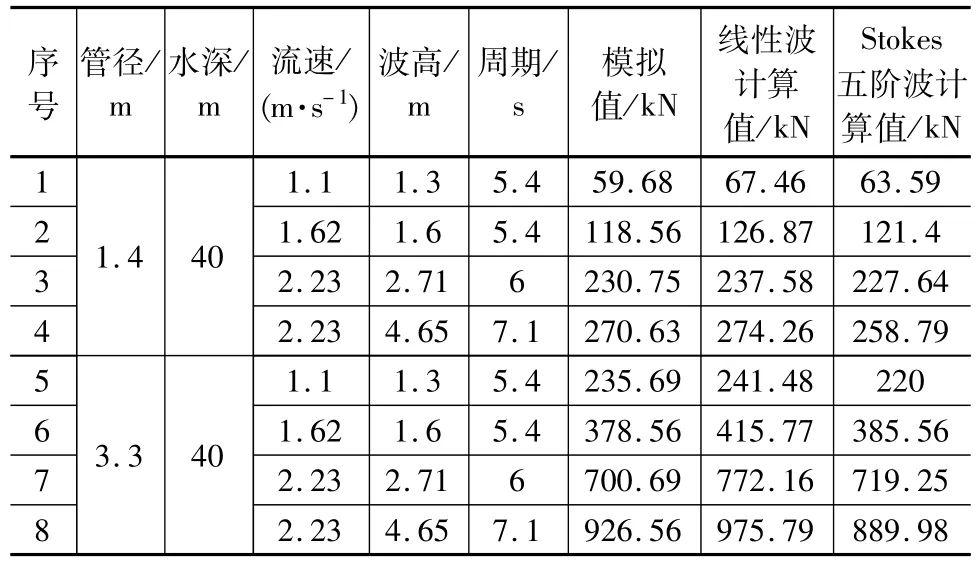
表3 波流耦合作用下钢管桩所受荷载

（6）周期对波浪力的影响

表4为不同周期工况下平台钢护筒上波浪力计算值。分析表中数据可知，钢护筒上的波浪力随着波浪周期的增大而减小。说明施工过程中周期小、频率快的波浪对钢护筒作用力更强。

表4 不同周期工况下平台钢护筒上波浪力计算值

4 结论

通过Morison理论公式和三维数值模拟方法对平潭海峡公铁两用大桥管桩上波流荷载进行研究，得到以下结论：

（1）管桩上波流荷载随着波高的增大而增大，且波流力Stokes五阶波理论计算与数值模拟值更相近，线性波理论计算值较模拟值大。

（2）在仅受波浪作用下，在一定水深范围内，管桩上波流荷载随着水深的增大而增大；随着水深的增加，波浪在深度方向的影响极剧减弱。

（3）管桩上波流荷载随着管径的增大而增大，且管径的变化对荷载的影响较为明显。

（4）管桩上波流荷载随波高、流速的增大而增大。规范理论公式计算忽略了波浪和水流的相互作用，跟实际情况存在较大差异。

（5）管桩上波流荷载随着波浪周期的增大而减小，即周期小、频率高的波浪对管桩作用力更强。