基于节约算法的车辆调度问题优化
王海玲,卢允辉
基于节约算法的车辆调度问题优化
王海玲,卢允辉
(厦门大学嘉庚学院,福建厦门,363105)
本文通过对于车辆调度现状建立了单车满载车辆的分送优化模型。首先对问题进行分析,将模型各个需求点的最小需求量作为约束,以总运输路径最短为目标,来确定车辆配送路线。并以节约算法的基本原理为基础,对模型进来具体求解优化。最后给出优化后的处理方法的优缺点分析,并且对解结果进行讨论和再优化。
车辆调度;节约算法;优化
引言
在物流系统中,时常会遇到车辆的路径规划问题,而求解方法有很多种,可分为最优化算法、动态求解算法和启发式算法三大类。C-W节约算法属于启发式算法。是一种被用来解决车辆数不固定情况下的车辆调度问题。该算法从起始出发按所需访问的所有点作出N-1条线路,计算合并任意两条路径后与之前未进行优化时的路径相比较,得出合并线路后所节约的路程量;然后再将节约的路程量按大小进行排序;最后依据排序结果以及附加的约束条件对合并后的路径进行判断线路是否合理,直到所有需要访问的点都被安排到线路当中。
本文根据对于车辆调度现状,建立了车辆的配送优化模型。通过计算,给出了优化后的处理方法对优缺点进行分析,最后对于求解结果进行讨论和再优化。
1 车辆调度问题概述
车辆调度问题最早是由Dantzig和Ramser于1959年提出来的[1],并且许多现实生活中的的实际问题的理论都可以归结于这一问题。由于应用前景广阔,所以成为运筹学与组合优化领域的研究热点[2]。随着越来越多的专家学者对车辆调度问题的研究不断深入和发展,最近几十年来,不但获得了很多有意义的成果,并且使得车辆调度在当下现实生活中能更好的被节约算法所解决。
车辆运输调度问题一般定义为:对一系列装货点和卸货点规划适当的行车路线,使车辆有序地通过它们,满足一定的约束条件,如时间窗口约束、车辆容量限制、车辆行驶里程限制、司机最大工作时间限制等,达到一定的目标如:车辆行驶路程最短、运输费用最少、使用车辆数最少、服务质量最高等[3]。
对于车辆调度问题,许多学者根据不同的标准,从不同的角度出发对车辆调度问题进行了不同的分类:
按照车辆载货物的情况分,有满载问题(货运量不小于整车负荷量)和非满载问题(货运量小于车辆容量或者一辆车服务多位客户)
按照车辆类型分,有单车辆类型问题(使用的所有车辆相同)和多车辆类型的问题(执行任务的车辆的类型和负荷能力不完全相同)。
按照任务特征分,有纯装载(纯卸货)问题,即集货或送货问题(车辆在所有任务点只装、卸货)及装、卸货混合问题,即集货送货一体化问题(每个客户有不同的装、卸点)。
按照任务的性质,有对弧服务问题(如邮差问题)和对点服务问题(如旅行商问题)以及混和服务问题(如交通路线的安排问题) 。
按照车辆是否需要返回车库的关系来分,有车辆开放问题和车辆封闭问题。
按照信息是否全部都是预先知道来分,有动、静态VRP问题。
按照不同的数学模型来分,有TSP问题(旅行商问题)VRP问题(车辆路径问题)和PDP(装载和卸载问题)。
按照车库数目分,有单车库对多客户问题和多车库对多客户问题。
按照优化目标来来分,有单目标问题和多目标问题[4]。
其中,车辆调度问题中最常见的问题之一就是VRP(Vehicle Routing Problem, 车辆路由问题),它是用来确定一些有容量限制的车辆在配送过程中的最优路径,必须经过每个访问点但不能重复访问[5。我们可以这样理解VRP问题:现有单个(或更多)出发点(也是终止点)和多个需要遍历访问的点,现在在出发点有配送的车队(车辆数量已知或未知但是都存在容量限制), 从出发点开始进行配送,并且必须经过所有需要访问服务的点。为了使得运输成本最低应该如何分配线路使得从出发点到所有需要访问服务的点的距离最短。VRP的解就是设计出一个或多个满足这样要求的最短配送路线,同时必须满足一系列的约束,可以包括货品体积约束、车辆需要进行保养和维护的里程数约束、车辆行驶路程约束、时间窗口约束等。
2 节约算法的基本原理
节约算法(节约里程法)的基本思路如图1和图2所示,设车库到客户A和B的距离分别为a和b。客户A和B之间的距离为c。车辆要向客户A和B分别运输货物,起点为车库。现有两种路径方式去实现,配送路径如下图箭头标注所示:

图1 未使用C-W算法前的路径前的

图2 使用C-W算法后的路径
在图1中,车辆的配送距离为2a+2b;在图2中,车辆的配送距离为a+b+c。由上图1的中的配送距离与图2的配送距离做差可以得到:


3 算法流程
根据前面所叙述的求解原理,给出具体求解步骤如下:
4 求解结果
以长荣物流(上海)有限公司福州分公司点为例o(图3中的点2),现向A、B、C、D、E五位客户运输货物,即图3中的1,3,4,5,6五点,单车最大载重15T。通过百度测量出各点到仓库的距离(Km)以及配送点到配送点之间的距离,点对点的最短距离的如表1所示,连线如图5所示,客户货物需求量如表1所示。
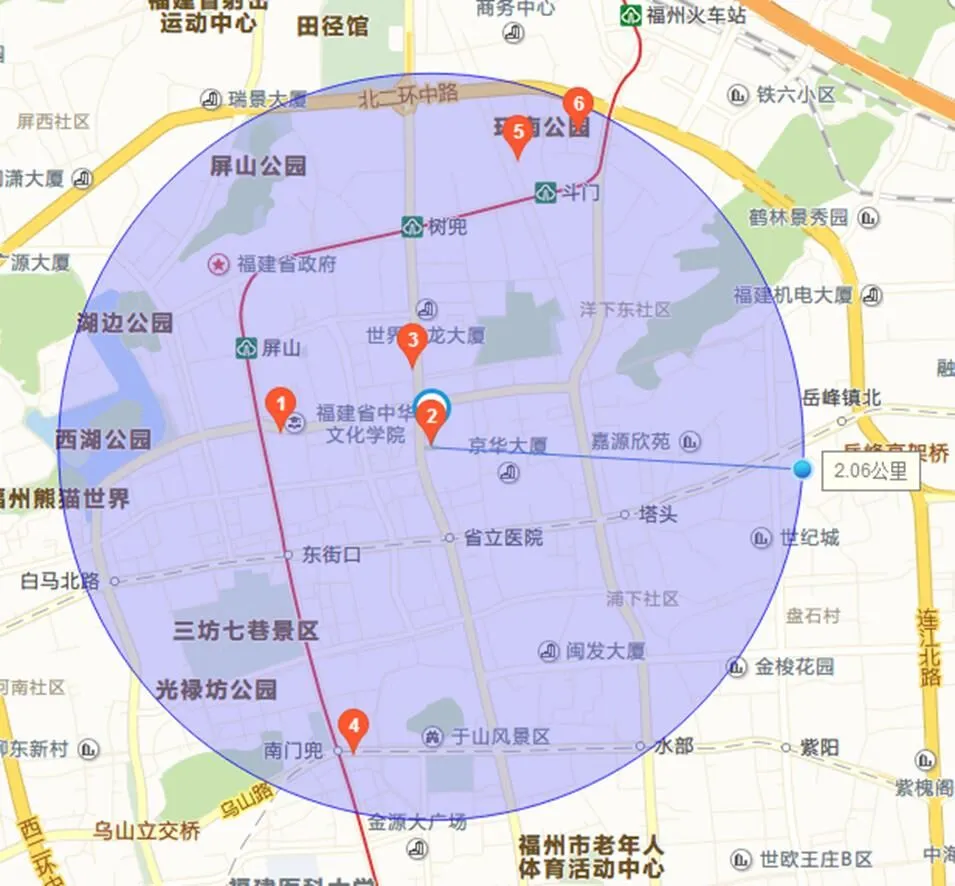
图3 仓储点及配送客户点图
仓库O与各客户之间的分布网络图4

图4 仓库与各点分布网络图

图5 各点之间相连连线
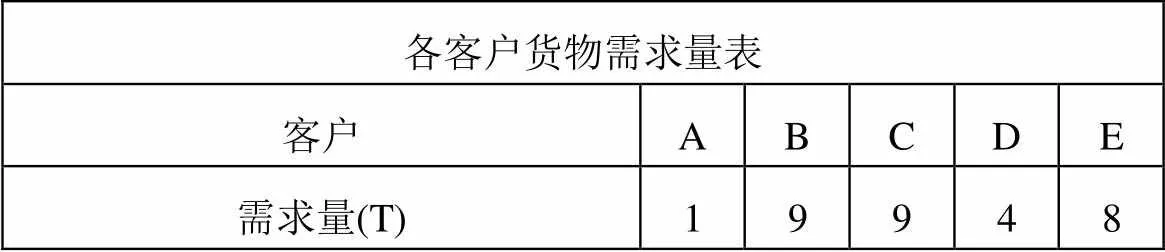
表1 各客户货物需求量表

表2 点对点距离表
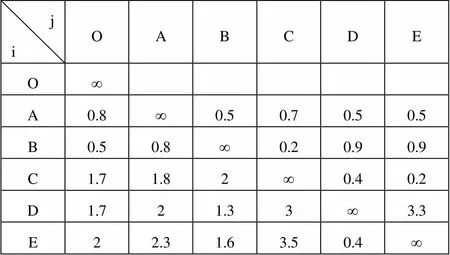
表3 路程节约值表
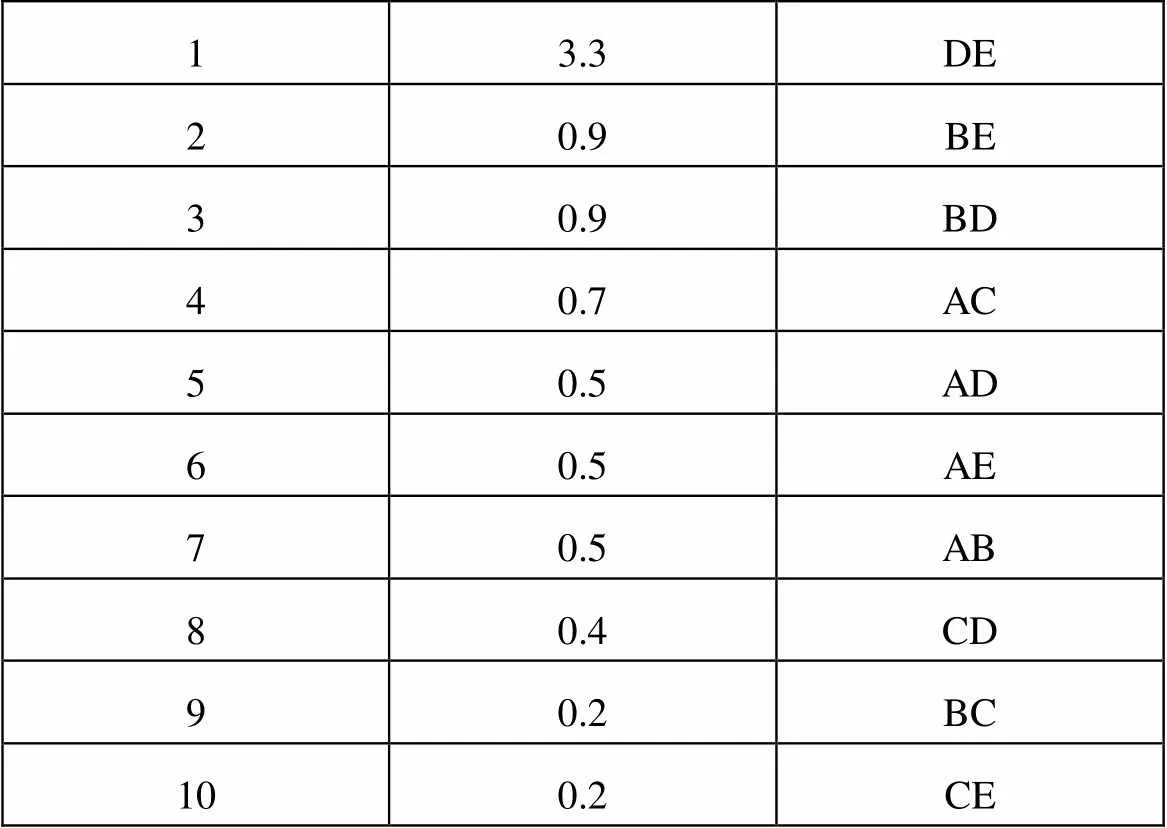
表4 节约值从大到小排列
由表4,可知节约值最大两个为3.3和0.9,连接D-E-B,因为配送车辆最大载重15T,D(T)+E(T)+B(T) =21T>15T,所以不可以连接,因此只连接DE两点。再按节约值来选择下一个连接对象为AC(0.7),载重为10T,所以可以连接,剩下B点单独配送。最终配送的三条线路如下:
(1)0-D-E-0 载重12T
(2)0-A-C-0 载重10T
(3)0-B-0 载重9T
路程较未优化前节约3.3+0.7=4(Km)。
节约配送车辆2辆。
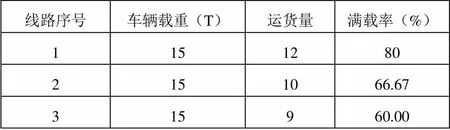
表5 车辆满载率情况表
由表5,可以看出当每个客户只能由一辆车服务的时候,多数车辆满载率太低。当客户需求可以分割,即单一客户的可服务车辆不限于一辆的时候,可以提高车辆的满载率。因此对此进行额外优化考虑。
此时默认车辆满载,对客户点的需求进行拆分,得到下表:

表6 各客户货物需求量表
根据表4和表6可以得出此时的配送线路为:
(1.1)O-D-E-B1-0 载重15T
(2.1)O-A-C-B2-0 载重15T
(3.1)O-B3-0 载重1T
路程较未优化前节约0.7(Km)。
节约配送车辆2辆。

表7 优化后的车辆满载率情况
此种配送方式虽然可以提高多数车辆的满载率,但是又由于配送车辆载重量的限制,导致当配送总量超出车辆载重配送总量上限时要多分配一台车辆。如本案例所示,虽然提高了其中两辆配送车辆的满载率,但导致其中一辆配送车辆的满载率只有6.67%。造成了资源的极大浪费。
此时如果将配送车辆装载重量类型多样化处理可以有效解决此种情况带来的资源浪费问题。
长荣物流(上海)有限公司福州分公司可将运输车辆业务外包给中泰运输公司,让其提供多种类的配送车辆。
此时配送车辆假设变为5T、10T、15T三种,且使单车满载率达到80%以上进行配送。
那么配送路线和车辆分配的情况就会变得多样化。以下列举其中一种情况,企业可根据实际情况例如优先考虑运输费用、运输时间等,进行车辆配送情况的选取。
以下为在节约路程值最大的情况下,优先考虑运输时间,只选取最低装载车辆(5T)进行同时配送来完成配送目的,将客户需求货物量进行拆分(表8),使其满足车辆满载率的运输要求:

表8 各客户货物需求量表
此时配送路线为:
(1)0-A-B1-0 载重5T 满载率100%
(2)0-B2-0 载重5T 满载率100%
(3)0-C1-O 载重4T 满载率80%
(4)O-C2-0 载重5T 满载率100%
(5)O-D-O 载重4T 满载率80%
(6)O-E1-O 载重4T 满载率80%
(7)O-E2-0 载重4T 满载率80%
路程较未优化前多了7.9(Km)。
配送车辆为7辆,比优化前多了2辆。
造成以上结果的原因为由于求解目标的不同导致节约路程变少,配送车辆数量也变多,但提高了车辆的满载率。同时载重数量小的车辆的运输费用也低,运输速度更快。节约配送时间也是企业可以获得利润之一,所以不影响企业采取该作为优化配送路线的选项。
结论
c-w节约算法思想简单,用来解决VRP问题时是一种很好用的算法,可以很快得出问题的满意解。在算法进行优化改进之后,可以节约了行驶路程和运输车辆的数目,从而降低了运输的成本,也可以提高的车辆的满载率,也可以节约配送所花费的时间等。根据不同的求解目的,可以对算法进行多种类、多方面的优化,从而可以得到满足尽可能多的约束又能获得相对最大的利润提升。
[1] Dantzig G, Ramser J. The truck dispatching problem. Management Science,1959,10(6):80-91.
[2] 祝崇隽,刘民,吴澄.供应链中车辆路径问题的研究进展及前景[J].计算机集成制造系统-CIMS,2001(11):1-6.
[3] 李军,郭耀煌. 物流配送车辆优化调度理论与方法。北京:中国物资出版社,2001.
[4] 《运筹学》教材编写组.运筹学[M].北京:清华大学出版社,2005,第三版.
[5] 顾坤坤. 不确定环境下物流配送有关问题的研究[D].中南大学,2009.
Optimization of Vehicle Scheduling Problem Based on C-W
Wang Hailing, Lu Yunhui
(Jiageng College, Xiamen University, Xiamen, Fujian Province, 363105)
In this paper, the distribution optimization model of vehicle load vehicle is established. Firstly, the problem is analyzed, and the minimum demand of each demand point of the model is used as the constraint, and the route of vehicle distribution is determined by the shortest path of the total transportation path. The factors affecting the transportation path are the sum of the distribution of each demand point and the driving distance of the vehicle. Based on the analysis, the model is based on the basic principle of the saving algorithm. Finally, the advantages and disadvantages of the optimized processing method are analyzed, the results are discussed and optimized.
Vehicle routing; C-W; Optimizing
10.19551/j.cnki.issn1672-9129.2019.03.002
F224
A
1672-9129(2019)03-0006-05

