粗糙度对水滴飞溅特性的影响规律研究
王 桥, 赵献礼, 刘森云, 肖京平, 马军林
(1. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000;2. 中国空气动力研究与发展中心 低速空气动力研究所, 四川 绵阳 621000)
0 引 言
飞机结冰严重威胁飞机的飞行安全[1-2]。为此,美国联邦航空管理局(FAA)在适航条例FAR 25部附录C中明确定义了飞机与其防除冰系统设计所必须考虑的结冰条件范围。然而,直到1994年10月31日在印第安纳州罗斯劳恩附近发生的ATR-72飞机坠毁事故,让人们对结冰条件范围有了重新认识。事故调查表明[3],冻雨在机翼除冰套之后副翼之前的上翼面形成了冰脊,冰脊导致了飞机的非指令滚转,而导致此次事故的冻雨超出了FAR 25部附录C定义的结冰条件, 出现了直径超过100 μm的过冷大水滴(Supercooled Large Droplet, SLD)。
研究人员发现,相比于FAR25附录C规定的常规水滴,SLD结冰条件的特点是存在一定数量较大直径的水滴且分布广,结冰环境温度较高[4],在运动、撞击过程中会发生变形、破碎和飞溅等显著的动力学行为[5-7],这些都可能导致更严重的结冰现象。因此,FAA于2014年11月在适航条例中新增了附录O“SLD结冰条件”及相关适航符合性要求。而在传统结冰数值模拟中,有两个最基本的假设[8-9]:一是水滴的刚性球假设,即水滴在运动过程中始终保持球形,不发生变形和破碎行为;二是水滴在碰撞固壁后不发生飞溅行为,即水滴撞击量与结冰量守恒。显然,在SLD条件下,这些假设不再成立,因此,需要发展SLD的动力学模型,以使得SLD结冰计算更加符合真实的结冰物理过程。
在SLD的动力学特性中,撞击飞溅特性主要指水滴铺展过程的最大铺展因子α(最大铺展圆的直径与初始水滴直径之比)、飞溅临界判则数K以及飞溅后子液滴模型(直径、速度、质量比等),这些量对结冰计算中的水滴收集率影响最大[10]。Scheller &Bousfield (1995)、Pasandideh-Fard(1996)、Clanet(2004)、Roisman (2009)、Eggers(2010)、Sen(2016)等[11-16]主要开展了水滴撞击固体表面的最大铺展因子α与撞击参数We、Re数等的函数关系研究,Tang[17](2017)研究了粗糙度Ra对最大铺展因子α的影响。Stow and Hadfield(1981)、Mundo(1995)、Cossali(1997)、Range and Feuillebois(1998)等[18-21]主要研究了We、Re、Oh以及粗糙度对飞溅临界判则数的影响规律。在飞溅子液滴模型研究方面, Lee and Ryou[22]、Stanton and Rutland[23]、Trujillo[23]等发展了基于不同统计方法的模型,其中美国LEWICE软件在3.0版本中加入了SLD飞溅模型,其子液滴模型就是在Trujillo模型的基础上改进而来的。然而,现有这些模型仍需发展,美国NASA在最近的结冰发展展望中仍然提到了需要发展SLD数值模型。就现有模型来看,在计算飞溅子液滴直径、速度等信息时,均未包含粗糙度Ra这一影响因素,而表面粗糙度对水滴撞击飞溅有重要影响已是公认的事实。因此,本文是在总结现有模型局限性的基础上,通过实验研究粗糙度对飞溅子液滴动力学的影响规律,希望为进一步完善、改进现有SLD飞溅模型提供支撑。
1 实验设计
1.1 实验系统
图1是实验系统总体布局图。实验系统主要由三部分组成:风道、水滴发生系统和高速摄像系统。风道温度可连续调节,最低达-15 ℃。
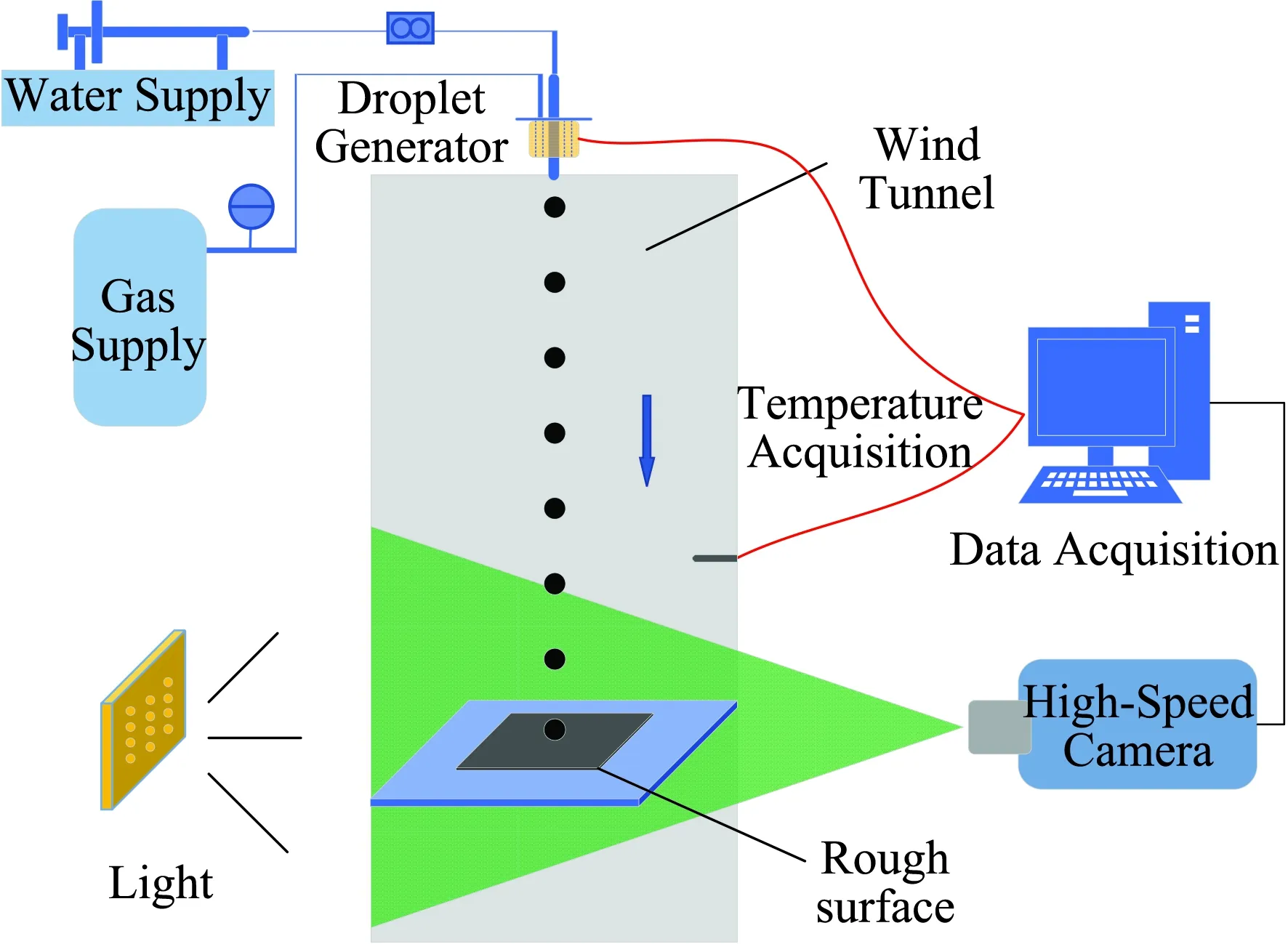
图1 实验系统总体布局图Fig.1 Schematic of experimental apparatus
风道由稳定段、收缩段、实验段以及扩散段组成。收缩段采用二元维多辛斯基曲线设计,收缩比为4,长0.2 m,其入口截面尺寸为0.3 m×0.3 m,出口截面尺寸为0.3 m×0.075 m;水滴的撞击过程发生在风道实验段,实验段长为 0.24 m,其截面尺寸为0.3 m×0.075 m,实验前对风道的湍流段进行了评估,风速为36.5 m/s时,湍流度<8.5%。
实验系统中最关键的是水滴发生装置,由水气两路组成,由于表面张力的作用,喷嘴会聚集较大水滴才能在重力作用下滴落,因此,采用均匀吹气的方式,通过微流量注射泵精确控制水滴的体积,产生所需直径的水滴。同时在风道和喷嘴口布置温度传感器,实时测量水滴和风道内气流的温度,当水滴温度满足过冷要求后,再进行吹气,释放水滴,这也是采用吹气控制水滴发生的原因之一。
实验采用MotionXtra的 HG-100K高速摄像机拍摄,设置拍摄像素为1024×1024 pixels,帧数为1500 fps,该相机可以精确地确定水滴的撞击速度和子液滴的飞溅情况。
1.2 实验方法
(1) 基本理论
水滴撞击动力学发展至今[26],主要由以下无量纲数控制着水滴撞击过程:

(1)
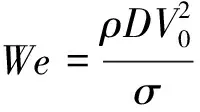
(2)
(3)
Mundo飞溅判则数K=Oh·Re1.25
(4)
其中,ρ、μ和σ分别代表水滴的密度、黏性和表面张力,D和V0分别代表水滴直径和撞击速度。
当然,考虑重力等加速度效应影响时,还有无量纲数Bo数、Fr数,但是因为水滴撞击表面有着剧烈的相互作用,重力效应可以忽略不计,因此可以不考虑这两个无量纲数。本文着重考虑粗糙度对水滴撞击过程的影响,遂引入无量纲数St:
St数St=Ra/D
(5)
其中Ra表征表面粗糙度,单位为μm。
为捕获水滴撞击过程,首先需要利用水滴发生器产生所需直径的单颗水滴,为保证水滴充分过冷,待水滴在喷嘴悬挂一定时间,温度由喷嘴处温度传感器获知。当水滴温度与气流温度基本一致时,通过吹气释放水滴,沿风道中心线运动,待其运动接近撞击表面时,触发高速摄像机记录整个撞击过程。为研究粗糙度对水滴撞击飞溅特性的影响,撞击表面贴上不同目数的粗糙度纸。
水滴直径、水滴速度这两个参数的测量都需要在实验前放置一个标尺进行标定,精度共同取决于相机分辨率、图像处理程序的精度。
(3) 实验条件
实验粗糙度范围是Ra=65~210 μm,温度范围是-1.5 ℃~23 ℃,水滴直径和速度根据实际测量结果确定,具体条次如表1所示,其中表第二列为实验用砂纸的目数,指在1平方英寸的面积上筛网的孔数,目数越低,筛孔越少,表面就越粗糙。

表1 实验条件Table 1 The experimental conditions
1.3 数据处理与误差分析
(1) 子液滴直径和速度
飞溅会形成多个子液滴,本文主要统计在撞击自由边缘飞溅方向正负5°范围内的清晰可见的子液滴,如图2黄色区域所示,分别测量左右该范围内子液滴的直径和速度,再将左右两个区域的值进行平均。

图2 水滴飞溅示意图Fig.2 Sketch of droplet splashing
水滴直径和速度测量精度和误差依赖于相机分辨率、图像处理程序以及拍摄频率。在本实验中,相机物距和焦距一定,在1024×1024分辨率,1500 fps拍摄速度的情况下,高速相片每一像素代表0.025 mm,两张照片时间间隔约为1/1500 s,根据实际数据处理情况,水滴直径的测量误差为±0.125 mm,速度的测量误差为±0.1875 m/s。
(2) 子液滴飞溅角度
(1)视在功率。视在功率主要值得是在电力线路中,电压和电流之间存在的差距与两者之间的乘积,通常在计算的过程中都是采用符号S表示,在计算的过程中通常都是有电流和电压进行相乘得出的一种功率形式。
水滴飞溅角度示意图如图3所示,其中θ为测量角度,ω为实际飞溅角度,φ为液滴与原点连线在xy平面的投影与x轴的夹角,由于相机是从正侧面(y-方向)进行拍照,因此所有不在xz平面水滴的测量角度θ都与实际飞溅角度ω存在一定偏差。
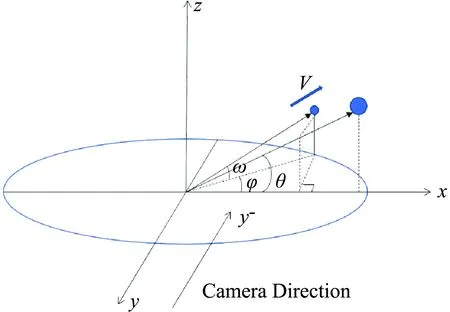
图3 水滴飞溅角度示意图Fig.3 Splashing angle of secondary droplet
根据如图3所示的几何关系,不在xz平面子液滴的真实飞溅角度ω与从图像中直接测量得到的角度θ之间的关系是:
tanω=tanθ·cosφ
(6)
如图4所示,由于高速相片中水滴的主要集中范围是θ<40°,φ<30°,因此真实飞溅角度ω与测量值θ具体偏差Δ=|θ-ω|<4°。

图4 飞溅角度误差分析Fig.4 Error analysis of splashing angle
2 结果与分析
图5展示的是温度23℃,粗糙度分别为St=0.143,St=0.07,St=0.037(Case 1、7、10)的三种典型实验系列高速相片,图片右上角为时间尺度,图5(d)为空间尺度。本文主要利用图像和拟合曲线处理软件,对 Case 1~22的所有高速相片中的子液滴进行统计分析,结果和分析如下。

(a) Case 1 (St=0.143)

(b) Case 7 (St=0.07)

(c) Case 10 (St=0.037)

(d) 标尺(图中每一格为1mm)
2.1 重复性实验结果
实验首先进行了五次重复性实验,实验工况为表1中Case 2至6,具体实验条件如表2所示。
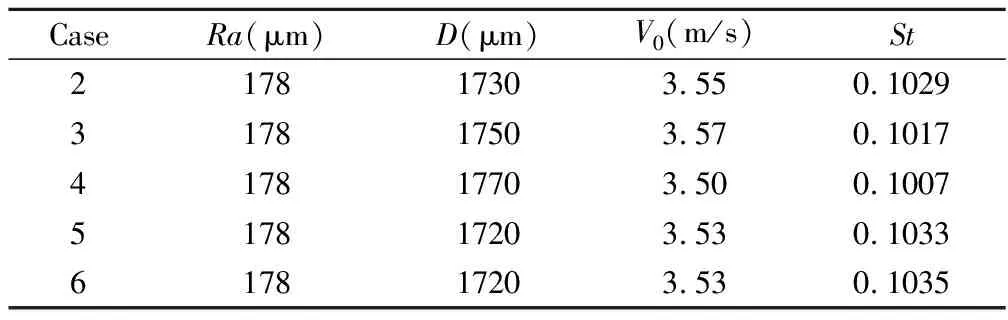
表2 重复性实验条件与结果Table 2 Conditions of repetitive test
为便于规律分析,将子液滴的直径d、速度Vs、角度ω分别无量纲化为:
β=d/D
(7)
γ=Vs/V0
(8)
δ=ω/ω0
(9)
五次实验子液滴的直径、角度、速度信息统计结果如图6所示,需要说明的是,每次实验子液滴直径、角度、速度值是指从图像中获取的左右两个飞溅方向(x+和x-)的平均值。从图6中可以看出,飞溅角度小于5°,子液滴无量纲直径小于0.03,无量纲速度小于10%,重复性结果一致性较好。
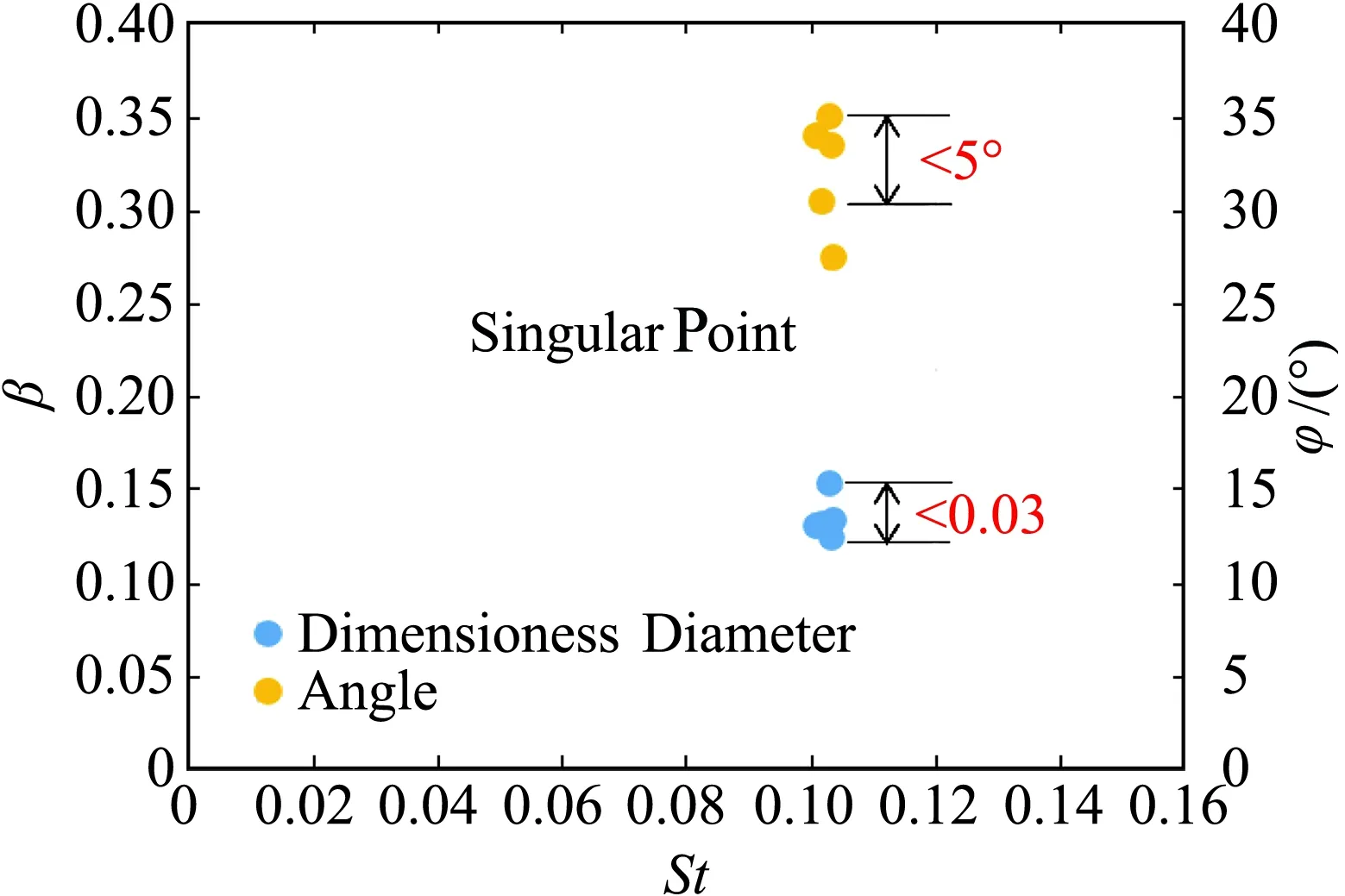
(a) 子液滴直径、角度重复性结果
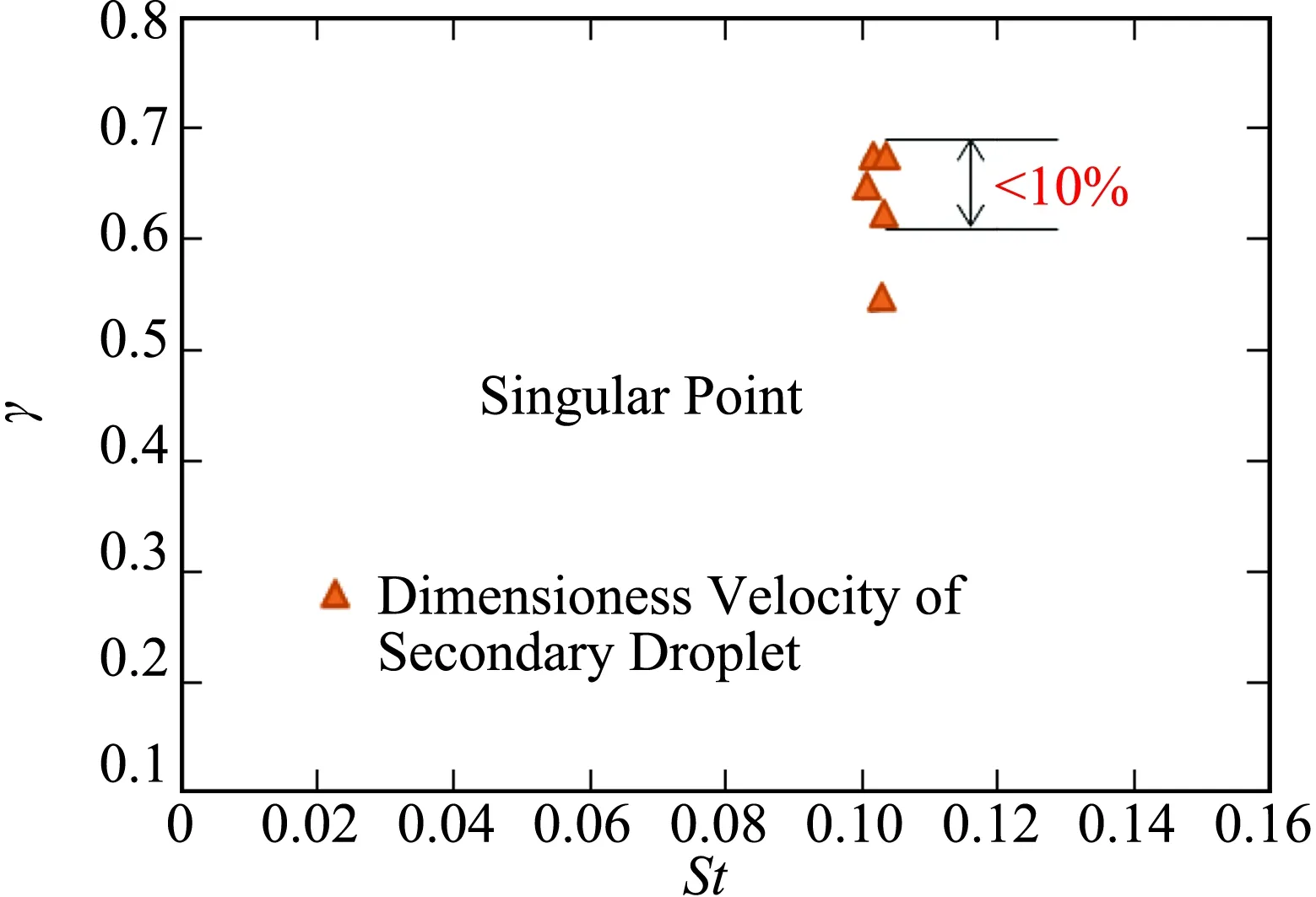
(b) 子液滴速度重复性结果
2.2 粗糙度对子液滴直径的影响
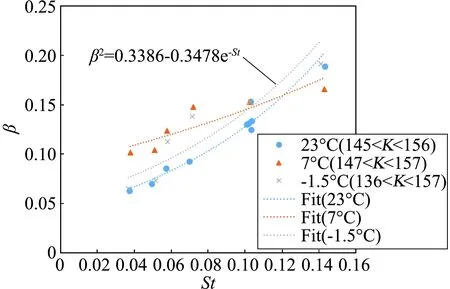
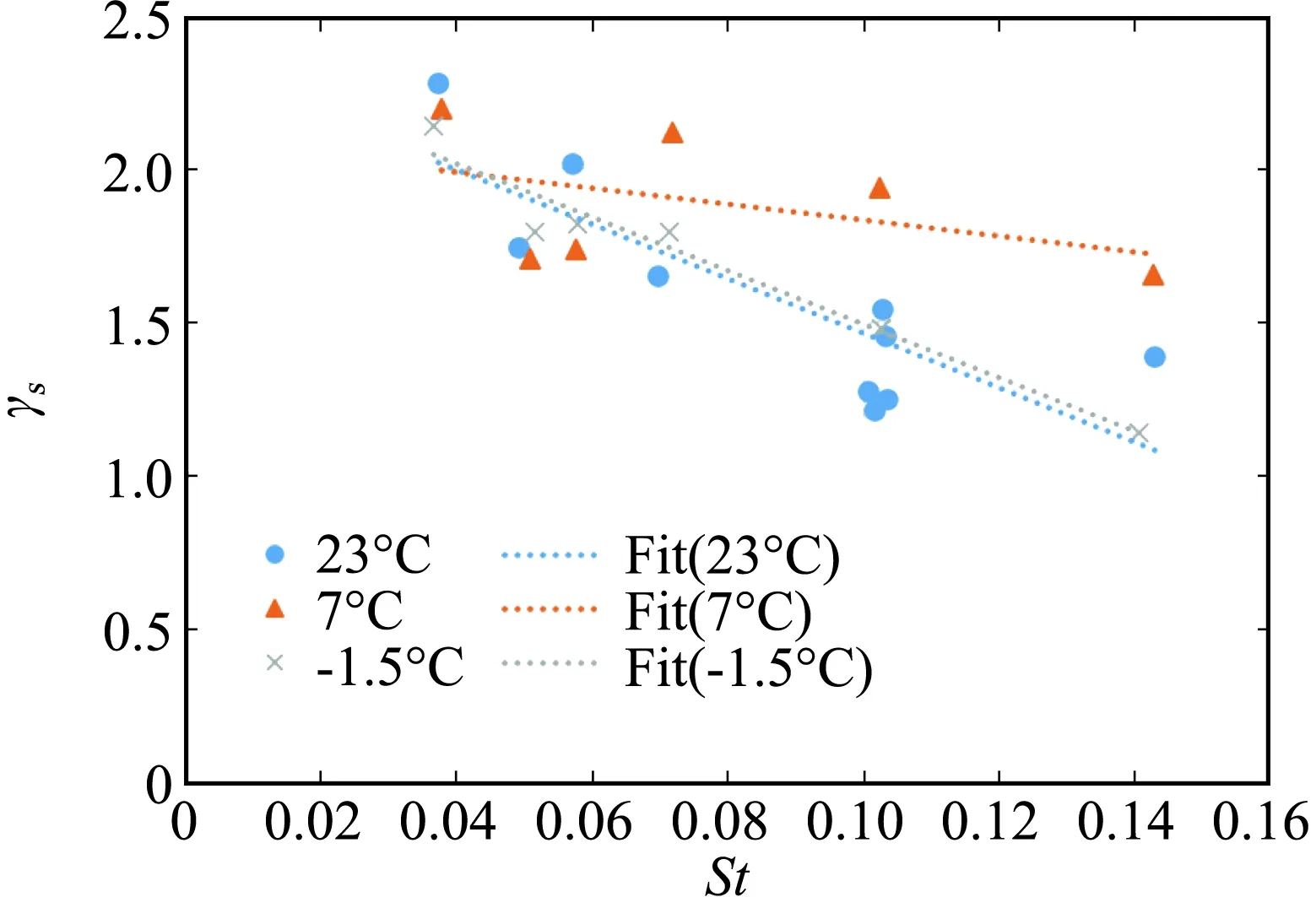
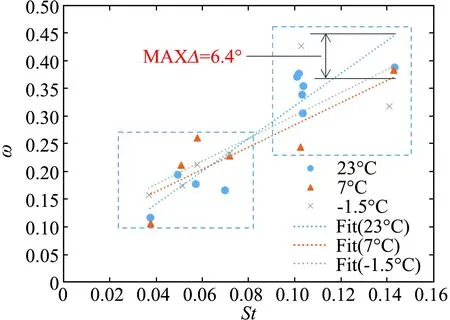
图7给出的是Case1~10在常温23℃条件下,不同粗糙度、不同撞击参数时子液滴无量纲直径的变化规律。图中蓝色曲线是美国知名结冰计算软件LEWICE 3.2版本给出的子液滴直径数学模型,由该模型可以看出,在不考虑粗糙度影响时,子液滴直径随着撞击参数K的增大较缓慢减小,而一旦引入粗糙度St的影响,子液滴无量纲直径β会在K变化较小的情况下,迅速减小,这也至少说明表面粗糙度对子液滴直径大小的影响在140 图7 子液滴无量纲直径随K值变化图Fig.7 Variation of the dimensionless diameter of sub-droplets with K value 图8是不同温度条件下,水滴无量纲直径随撞击参数K的变化规律。从图中可以看出,水滴温度的影响较小,无明显规律,故以-1.5℃的拟合曲线代表St对β的影响模型: β2=0.3386-0.3478e-St (10) 图8 不同水滴温度下子液滴无量纲直径随St值变化图Fig.8 Variation of the dimensionless diameter of sub-droplets with St value at different temperatures 图9(a)、(b)分别是飞溅子液滴法向(z+)和切向(x+和x-)速度随St值的变化规律。从图中可以看出,呈现了相反了的变化规律,随着St值的增大,γn增加,而γs减小,这是因为实验初始水滴垂直撞击粗糙表面,入射角为90°,越粗糙的表面,两个或几个粗糙颗粒之间的波谷越深,越容易阻碍水滴在撞击铺展或者飞溅时向切向方向运动,而在力的相互作用下,会把更多的能量提供给了与入射方向相反的方向。 在撞击参数140 (11) 切向:γs=8.1967+9.3549St1/2lnSt (12) (a) 子液滴法向速度γn (b) 子液滴切向速度γs 图10是不同温度条件下,子液滴无量纲角度随撞击参数K的变化规律。由于水滴几乎均垂直撞击,因此,无量纲角度计算式(9)中ω0取为90°。从图10中可以看出,子液滴无量纲角度δ与粗糙度St呈现正相关,并且随着St的增大,温度对δ的影响开始显现,但也不是特别明显,在实验范围中,最大差值仅为6.4°,也只比统计偏差高出2°,因此,温度影响相比粗糙度影响量仍然是小量。 图10 不同子液滴温度下子液滴无量纲角度随St值变化图Fig.10 Variation of the dimensionless angle of sub-droplets with St value at different temperatures 在不考虑温度影响的情况下,在撞击参数140 ω=0.7642+0.1936lnSt (13) 本文利用水滴撞击实验系统,开展了水滴撞击不同粗糙度表面的动力学实验,研究了表面粗糙度对水滴撞击飞溅特性的影响规律,通过数据分析得出以下结论: 1) 在撞击参数140 2) 粗糙度对子液滴法向和切向速度的影响规律不同,随着St值的增大,γn增加,而γs减小。 3) 子液滴无量纲角度δ与粗糙度St呈现正相关,并且当St>0.1时,温度对δ的影响开始显现,但相比粗糙度仍然是小量。
2.3 粗糙度对子液滴速度的影响
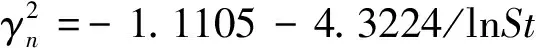

2.4 粗糙度对子液滴角度的影响
3 结 论

