龄期对碾压混凝土双K断裂参数影响的试验研究

，，，，，春蕊

(1.辽宁工业大学 土木建筑工程学院，辽宁 锦州 121000；2.天津市赛达伟业有限公司，天津 300000； 3.西安理工大学 水利水电学院，西安 710048；4.潍坊市公路路桥工程建设开发中心，山东 潍坊 261061)

1 研究背景

碾压混凝土在我国高坝建设中得到了大量的应用，但与普通混凝土的断裂性能得到了较为系统的研究不同[1-4]，目前对于碾压混凝土的断裂性能的研究仅限于试件尺寸、骨料级配等因素[5-7]。有学者通过三点弯曲梁试验法提出碾压混凝土断裂韧度存在着尺寸效应，并得到所适用的尺寸效应公式[8]，但关于龄期对碾压混凝土断裂韧度影响的研究则相对较少。而目前关于混凝土类准脆性材料的断裂模型有裂缝带断裂模型[9]、虚拟裂纹模型[10]、双参数断裂模型[11]、等效裂缝模型[12]、双K断裂韧度模型[13]和尺寸效应模型[14]等。其中，双K断裂理论以其清晰的理论模型、简单的实验操作方法和双K断裂参数计算方法而被我国的水工断裂试验规程所采用。

本文以双K断裂理论为基础，采用楔入劈拉法对不同龄期的碾压混凝土试件进行断裂试验，研究龄期对碾压混凝土双K断裂韧度、有效裂纹扩展量等参数的影响，总结了不同龄期碾压混凝土断裂参数的变化规律。

2 试验概况

2.1 试验设计

为探究不同龄期碾压混凝土楔入劈拉试件的断裂特性，试验共浇筑了龄期为28，60，90 d的3组共18个楔入劈拉试件，缝高比(缝的长度与试件高度之比)均为0.4,试件尺寸均为150 mm(长)×150 mm(宽)×150 mm(高)，分组编号分别为RCC-28，RCC-60，RCC-90，其中28，60，90代表试件的龄期。试件具体参数见表1。

表1 试件尺寸和参数Table 1 Dimensions and parameters of specimens

采用标号32.5普通硅酸盐水泥，Ⅱ级粉煤灰，细度模数为2.6的天然中砂，粒径为5～20 mm的一级配碎石，自来水，高效减水剂。配合比为水∶水泥∶粉煤灰∶砂∶石子∶外加剂=0.97∶1∶0.67∶6∶9.55∶0.013，水胶比为0.58，砂率为38%。采用木模浇筑，养护室标准养护成型。

2.2 试验过程

试验加载装置如图1(a)所示，所有试验均在20 t电液伺服试验机进行，以2×10-2kN/s的速度对试件进行加载并严格控制加载速率均匀连续，采用量程为0～50 kN的荷载传感器，裂缝口张开位移采用夹式引申仪，裂缝尖端及韧带方向的应变采用30 mm电阻应变片进行测量。试验的试件采用附着式振动器分2次碾压成型，在试件达到试验所需龄期后，需对试件裂缝一侧粘贴尺寸为150 mm×50 mm×30 mm(长×宽×高)的大理石，粘贴前需对试件的粘贴面进行打磨处理并使表面不平整度<0.5%，清洁后使用建筑结构胶粘贴牢固，图1(b)为缝高比0.4的试件简图。

图1 试验装置及试件简图Fig.1 Test device and diagram of specimen

2.3 双K断裂理论

20世纪80年代，徐世烺[15]结合大量混凝土断裂的试验，以应力强度因子为参量提出了双K断裂模型，该模型引入失稳断裂韧度和起裂断裂韧度作为裂缝失稳和起裂的控制参数，并结合虚拟裂缝方法和等效弹性方法，使试验方法简易可行，便于计算，同时考虑了双参数模型中所忽略的塑性变形影响，物理意义明确；其通过起裂断裂韧度和失稳断裂韧度将混凝土断裂过程分为3个阶段：起裂、稳定扩展和失稳扩展。具体描述如下：

2.4 双K断裂参数的计算

我国《水工混凝土断裂试验规程》(DL/T 5332—2005)[16]基于双K断裂理论提出了双K断裂参数的计算公式。这里采用规程中楔入劈拉试件双K断裂参数的计算公式，用于计算与碾压混凝土相关的各项参数。

2.4.1 弹性模量E的计算公式

在裂缝未发生扩展前，即荷载未达到起裂荷载，此时碾压混凝土处于线弹性阶段。根据试件F-V曲线(试件的实测荷载-裂缝口张开位移曲线)的上升段之直线段任意一点，确定初始柔度ci=Vi/Fi，计算弹性模量E。其E的计算公式为

(1)

式中：a0为裂缝的初始长度；t为试件厚度；h为试件高度；h0为装置夹式引伸仪刀口厚度。

2.4.2 临界有效裂缝长度ac的计算

试件承受最大荷载时对应的临界有效裂缝长度ac是计算失稳断裂韧度的重要参数，计算公式为

式中：CMODc为裂缝口张开位移临界值；FHmax为最大水平荷载。

2.4.3 失稳断裂韧度

楔入劈拉试件的失稳断裂韧度计算公式为

(3)

其中，

f(α)=3.675[1-0.12(α-0.45)](1-α)-3/2，

式中：Fmax为最大荷载；mg为楔形加载架的重力。

2.4.4 起裂断裂韧度

楔入劈拉试件的起裂断裂韧度计算公式为

(4)

其中，

f(α)=3.675[1-0.12(α-0.45)](1-α)-3/2，

式中：PHini为起裂水平荷载；Pini为起裂荷载。

3 试验结果与分析

3.1 试验现象

加载初期，楔入劈拉试件开始受力，此时混凝土内部产生裂缝并扩展，随荷载的增加，裂缝尖端开始出现肉眼可见的裂缝并稳步向下扩展，同时裂缝的张口位移逐渐增大；当荷载达到最大值时，混凝土的内部黏聚力难以承受外部荷载，裂缝的张口位移快速扩大，与此同时裂缝开始失稳扩展；此后荷载逐渐下降，直到荷载下降为0时，试件呈劈拉破坏。

3.2 起裂荷载的确定

图2 试验实测的P-ε曲线Fig.2 Measured P-ε curve

《水工混凝土断裂试验规程》中确定的起裂荷载是试件F-V曲线上升段从直线段转变为曲线段的转折点所对应的荷载，但在实际测量中线段转折点的确定难度较大，并存在一定误差，因此采用该方法确定起裂荷载存在难度大和准确性较低这2个问题。然而起裂荷载的确定是计算起裂断裂韧度的关键。为此，本文采用在裂缝尖端布置电阻应变片法[11]来测定起裂荷载。从加载开始，裂缝两侧混凝土不断聚集能量，随荷载的增加，裂缝尖端的应变值基本呈线性增长趋势，直至应变值达到极值后出现回滞，表明测点间有裂缝出现，混凝土聚集的能量得到释放，该测点开始得到卸载，其中应变开始回缩时所对应的荷载值即为起裂荷载。如图2所示。

图3为不同龄期碾压混凝土条件下的F-V曲线。由图3可看出不同龄期下的试件F-V曲线在加载初期基本呈线性关系，裂缝张口位移增长缓慢，无宏观裂缝产生；随荷载的增加，F-V曲线出现拐点，荷载与裂缝开口位移开始呈非线性关系发展；当荷载增加到最大值后，荷载开始迅速下降，同时裂缝开口位移迅速增大，直至试件破坏。与此同时，由F-V曲线可知，龄期越大，试件的失稳荷载越大，裂缝的张口位移变化越快，试件的延性越差。

图3 不同龄期下碾压混凝土试件的F-V曲线Fig.3 Curves of F-V of RCC specimens of different ages

3.3 结果分析

根据已知参数，通过式(1)和式(2)分别计算弹性模量E和临界有效裂缝长度ac，进而按式(3)求得各试件的失稳断裂韧度，采用本文中所提到的起裂荷载确定方法得到各试件的起裂荷载并通过式(4)计算其起裂断裂韧度。具体计算结果见表2、表3，其中Δac为裂缝亚临界扩展量，Δac=ac-a0。

由表2和表3可看出试件龄期为28，60，90 d所对应的起裂和失稳荷载的均值分别为0.82 kN和1.52 kN、0.84 kN和1.911 kN、1.78 kN和3.06 kN,其中起裂和失稳荷载的比值介于0.441～0.584。碾压混凝土强度随龄期增大而增大，随强度增大，试件的抗裂性能越好其对应的起裂荷载就越大，同时起裂荷载占失稳荷载的比值越重，这与文献[17]所述普通混凝土的规律有相似之处。

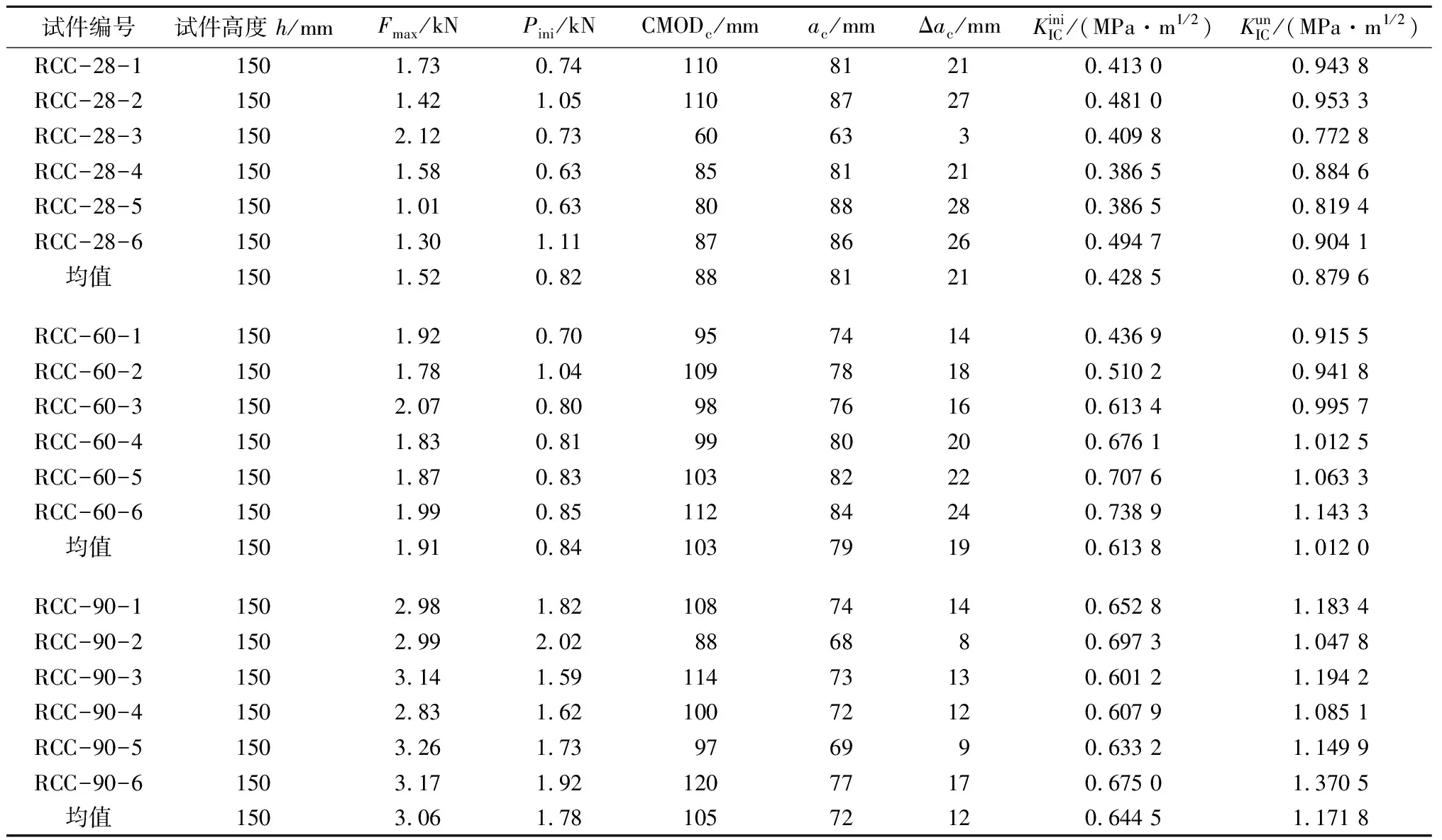
表2 碾压混凝土双K断裂参数Table 2 Double-K fracture parameters of RCC

表3 碾压混凝土断裂参数比值Table 3 Ratios of fracture parameters of RCC

为了更直观地观察断裂参数随龄期的变化规律，这里将不同龄期的双K断裂参数和起裂与失稳断裂参数比值绘制如图4所示。

图4 不同龄期下的断裂韧度及起裂韧度与 失稳韧度的比值Fig.4 Curves of the fracture toughness and the ratio of initial fracture toughness to unstable fracture toughness of specimens at different ages

由图4(a)可看出，随龄期的增加，起裂断裂韧度和失稳断裂韧度均呈逐渐上升的趋势，龄期从28 d增加到90 d，起裂断裂韧度均值从0.428 5 MPa·m1/2增加到0.644 5 MPa·m1/2，失稳断裂韧度均值从0.879 6 MPa·m1/2增加到1.171 8 MPa·m1/2，其中起裂断裂韧度增加了0.216 0 MPa·m1/2，失稳断裂韧度增加了0.292 2 MPa·m1/2。由图4(b)可以看出，不同龄期试件的起裂断裂韧度和失稳断裂韧度的比值基本在0.5～0.6，说明碾压混凝土结构的延性变化较小。

图5 裂缝长度随龄期的 变化曲线Fig.5 Relationship between crack length and age

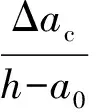
4 结 论

本文通过对龄期为28，60，90 d的3组18个碾压混凝土楔入劈拉试件的断裂试验，结合双K断裂理论，分析断裂过程中断裂参数的变化，得出以下结论：

(1)起裂荷载和失稳荷载均随龄期的增大而增大，其中起裂和失稳荷载的比值介于0.440 5～0.583 5，伴随着龄期的增加，起裂荷载占失稳荷载的比重越大。

(2)不同龄期条件下，碾压混凝土劈拉试件的起裂断裂韧度与失稳断裂韧度的比值趋于稳定，且起裂断裂韧度与失稳断裂韧度均随龄期的增大而增大，其中起裂断裂韧度均值从0.428 5 MPa·m1/2增加到0.644 5 MPa·m1/2，增加了0.216 0 MPa·m1/2，失稳断裂韧度均值从0.879 6 MPa·m1/2增加到1.171 0 MPa·m1/2，增加了0.292 2 MPa·m1/2。

(3)临界有效裂缝长度和裂缝亚临界扩展量随龄期的增加呈下降趋势，表明龄期越长，试件的延性越差，越容易发生脆性破坏。但裂缝扩展程度受龄期的影响较小。