强透水地基岸墙稳定性与墙前水位骤降关系研究

，，，

(1.华中科技大学 土木工程与力学学院,武汉 430074; 2.广州市水务工程建设管理中心, 广州 510640)

1 研究背景

潮汐、洪水退落和水库开闸降水等水位快速下降和长时间暴雨后墙后水位抬高往往存在挡土墙失稳的安全隐患。目前对挡土墙设计中墙前、墙后水位的取值还不明确，关于这方面的研究也比较匮乏。当前挡土墙设计中墙前、墙后水位关系的假定往往并不是最不利条件的假定，因而研究水位骤降条件下挡土墙稳定性规律以及墙前、墙后水位关系对挡土墙安全设计有重要意义。

目前关于水位骤降条件下挡土墙稳定性的研究中，挡土墙稳定性的判断是依据实际工程施工条件和调度使用状况，利用工程上几个特征水位组合作为控制。《重力式码头设计与施工规范》[1]规定，墙后设置抛石棱体或回填料粗于中砂时，可不计算剩余水头；当墙后回填中砂或比中砂更细的填料时，对受潮汐影响为主的码头，剩余水头的标准值可采用1/5～1/3平均潮差；针对河港其计算值应依据墙前水位及墙后地下水位状况确定；针对暴雨导致的墙后地下水位上升的码头，尚宜计算残余水压力。

《河道整治设计规范》[2]附录B建议水位骤降取1 m。不少挡土墙工程的设计，针对水位骤降条件下墙前、墙后的水位差的组合采取了简化处理，如墙前水位采用设计(校核)洪水位、墙后水位采用平墙顶(或地下最高水位)，或取墙前洪水位高度骤降到常水位、墙后水位高度取墙前洪水位下降高度的60%[3]。Terzaghi[4]通过研究发现，在持续性降暴雨的过程中，水不断渗入土体中将产生渗流，土中的渗流将产生稳定的渗流场，从而导致挡土墙上水压力的增加，致使有效应力减少，最后使挡墙失效。谢新宇等[5]认为水位变化是影响挡土墙路基稳定性的重要因素，水位缓慢变化与骤然下降对路基产生的影响不同。钟恒昌等[6]认为通常直接采用工程的几个特征水位组合作为控制挡土墙稳定计算水位组合进行分析不合理，这种水位组合往往并不是挡土墙抗滑稳定计算的最不利组合，最危险工况可能出现在特征水位区间内的某个水位组合。Barros和Santos[7]假定挡土墙后水位为定值，用数值模拟的方法分析了墙面排水条件下墙后水压的大小，并采用库伦理论分析了墙后主动土压力的大小。在他们的最新论文中[8]，墙后渗流面的位置可随时间变化，并以其为基础进一步推导出主动土压力的表达式，但是该研究并没有讨论墙前后水位变化的规律以及其与墙体参数及墙前水位下降速度的关系。

综上所述，在墙前水位骤降条件下，如何正确评价挡土墙稳定性以及墙前、墙后的水位关系尚无深入研究。本文以箱型岸墙为研究对象，结合大型模型试验对Seep/w渗流分析做数值标定，以此为理论依据结合具体工程案例，分析箱型岸墙抗倾、抗滑稳定性与水位骤降之间的关系，并探讨墙前、墙后水位关系与稳定性最不利时刻之间的关系。本文可为工程上挡土墙的安全设计提供参考价值，对正确评估水工挡土墙的安全度有重要意义。

2 数值模拟的模型验证

本文研究基于Seep/w渗流软件[9]，为确保结果的可靠性，利用大型模型试验对数值模拟进行标定，为后文研究提供依据。

2.1 模型设计介绍

模型试验在自制的大型模型箱内进行墙前水位骤降，降水速度取广州某河流某次洪水最不利降落时段的降水速度0.5 m/h。试验中其他物理参数依据《土工试验方法标准》室内试验测得(见表1)。

表1 填土物理参数Table 1 Physical properties of the backfill soil

试验填土高度为2 m，在填土底部临近挡墙部位填充高0.2 m，长0.56 m的碎石，另一侧蓄水空间同样填充高为0.2 m碎石，剖面图如图1所示，碎石渗透系数为18 cm/s。试验用土量约4.2 m3，其填充方法为分层填充，分层击实，并每隔0.2 m采用环刀法进行密实度检测，保证模型制样的均匀性。

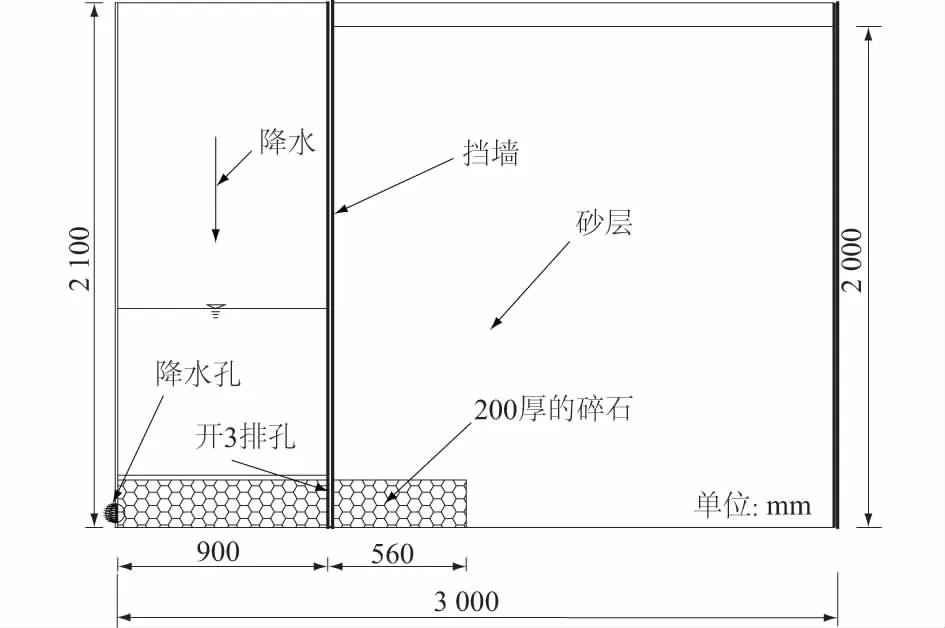
图1 试验模型剖面图Fig.1 Illustration of the test model

在箱内填土纵轴面上预埋振弦式通气型渗压计，用于监测墙前水位骤降条件下墙后填土内孔隙水压的变化规律，渗压计分3层埋设，其分布规律及编号如图2所示。

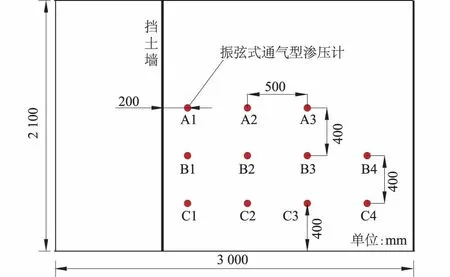
图2 振弦式通气型渗压计正剖面分布Fig.2 Layout of the vibrating string osmometers

2.2 数值模拟简介

根据模型试验的原模型，在Seep/w中建立有限元网格模型如图3所示。图中DEF代表不透水边界，DG代表模型初始水头边界，GH代表墙前水位下降初始高度；中砂和碎石材料参数与模型试验相同且尺寸完全一样；图中A1-A3、B1-B4、C1-C4表示渗压计分布，与模型试验位置相同；网格采用四边形，其网格尺寸为0.05 m。

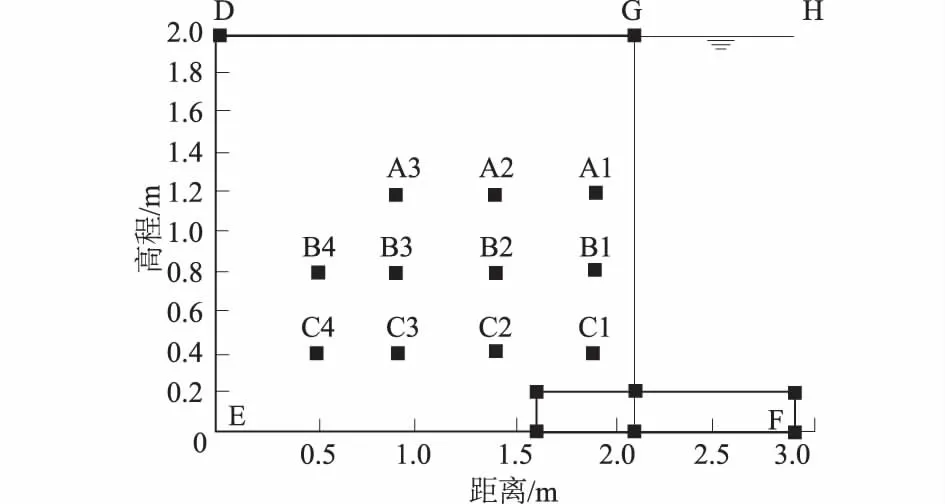
图3 数值分析模型Fig.3 Numerical model

数值模拟时土的体积含水量函数和渗透系数函数由Seep/w程序中内置典型填土的体积含水量曲线和渗透系数函数根据试验用土的性质修正得到。

表2 箱型岸墙设计有关参数Table 2 Design parameters of the caisson bank wall

2.3 模型试验与数值模拟孔压的对比分析

将试验中电磁流量计监测的降水速度数据导入Seep/w模块后，对模型进行瞬态渗流分析，提取渗流分析前标定渗压计位置点的压力水头随时间变化关系图，并与模型试验所得结果对比分析，其结果如图4所示。

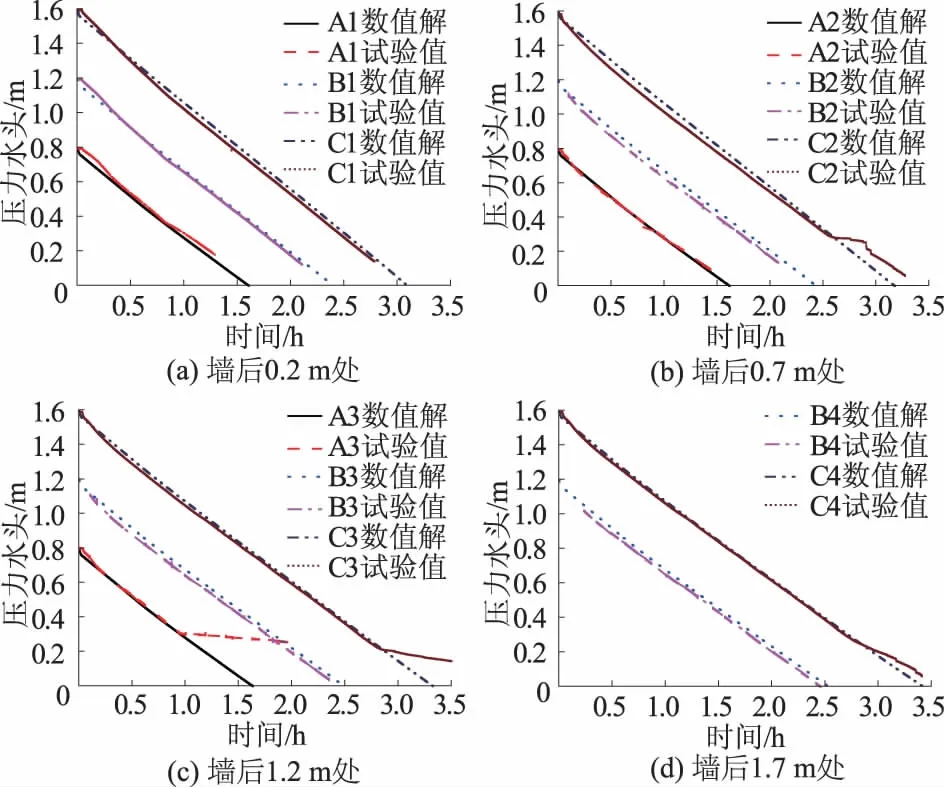
图4 测点压力水头试验值与数值解对比Fig.4 Comparison of water head between experimental and numerical results

由图4可知：数值模拟计算得到的压力水头与试验测得的压力水头基本吻合，因此在保证参数可靠性的前提下，本研究所采用的数值模型能够较准确模拟墙前水位骤降时墙后水压的变化，可用于研究实际工程中水位骤降对水工挡墙稳定性的影响。

3 水位骤降条件下箱型岸墙稳定性影响因素研究

本节依据前面的研究为基础，利用Seep/w软件对广州某河流箱型岸墙的稳定性影响因素及墙前、墙后水位关系进行分析，并探讨其与岸墙稳定最不利时刻之间的关系，以供水工挡土墙设计参考。

3.1 箱型岸墙断面设计

参考《水工挡土墙设计规范》[10]规定对箱型岸墙进行设计，墙后填土与岸墙顶部持平，填土范围内加10 kPa均布超载。设计相关参数取值如表2所示。

箱型岸墙抗倾、抗滑稳定计算公式如下。

抗倾稳定计算：

(1)

抗滑稳定计算：

(2)

式中：K0为抗倾稳定安全系数；∑MV为抗倾覆力矩(kN·m)，是所有竖向力的力矩之和；∑MH为倾覆力矩(kN·m)，是所有水平力的力矩之和；Kc为抗滑稳定安全系数；∑V为作用于墙体上全部垂直力的总和(kN)；∑H为作用于墙体上全部水平力的总和(kN)；f为墙底与基础之间的摩擦系数，取f=0.6。

岸墙断面尺寸如表3所示，根据表2参数及式(1)、式(2)计算可得岸墙设计骤降工况下(墙前水位从墙顶骤降1 m，墙后水位与墙顶齐平)抗倾、抗滑稳定系数分别为K0=2.08，Kc=1.35，满足规范要求。

表3 箱型岸墙截面设计尺寸Table 3 Cross-sectional dimensions of the caisson wall

3.2 数值模型建立及有关参数确定

岸墙典型断面如图5所示。地基从上往下依次为2 m厚的砾石层和强风化岩，回填砂土内侧为旧有浆砌石岸墙，相对于回填砂土和砾石地基，可认为旧岸墙、强风化岩和新岸墙为不透水材料。在中砂和砾石层地基交界面处填充有0.3 m厚的碎石，从保守考虑，取碎石渗透系数等同砾石，均取1×10-2cm/s；碎石与中砂之间铺有一层反滤土工布，土工布渗透系数取k=0.1 cm/s。

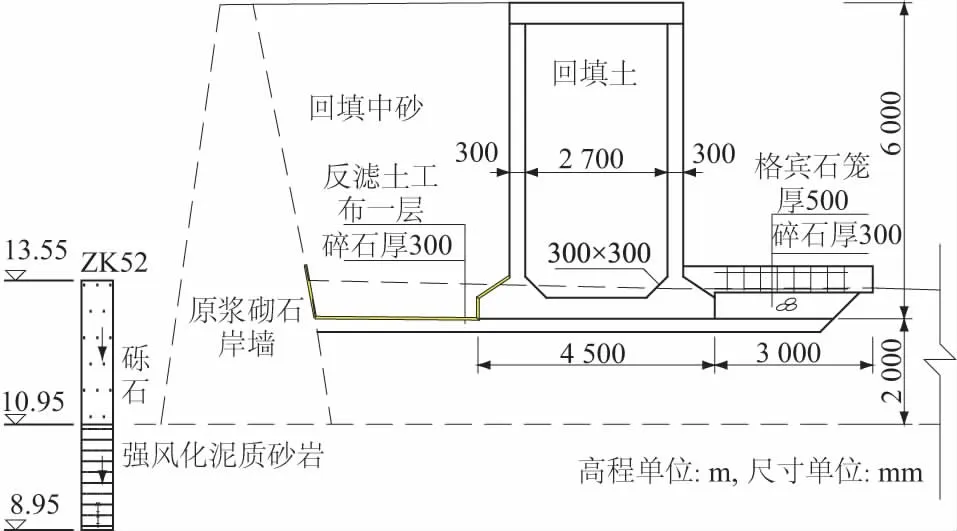
图5 箱型岸墙典型断面Fig.5 Typical cross-section of the caisson bank wall

王忠权等[11]对钱塘江海塘原型进行渗透试验研究，发现埋设于石塘后侧块石堆内的测压管及渗压计量测到的水位变化与石塘前的水位变化几乎同步，说明石塘下部抛石基床的渗透性很大，可假定为联通体。本文墙前干砌石和石笼压脚为强透水，参考王忠权等[11]研究成果，在渗流分析中可不予考虑。同时本研究不考虑墙身排水孔及结构缝的排水作用，假定墙后地下水只能通过墙下部砾石地基排出。

据此利用Seep/w软件分析岸墙在墙前降水速度分别在2,1.5,1,0.5 m/s 4种不同降水速度，不同墙后填土渗透性(饱和渗透系数分别取4×10-4,1.54×10-3,2.42×10-3,3.27×10-3,3.8×10-3cm/s)下的稳定性及墙前、墙后水位关系。墙前墙后的初始水位均与墙顶齐平，墙前水位降落为从墙顶降落到墙底。墙后水土压力计算截面取通过墙踵的垂直截面(以下简称计算截面)。

由于工程地质条件较好，地基承载力在各种工况均可满足规范要求，本文不对地基承载力进行研究，文中提到的稳定性均指抗倾稳定性和抗滑稳定性。

3.3 数值分析墙后水压分布特点及水土压力计算方法

以岸墙在降水速度0.5 m/h，墙后填土渗透系数为4×10-4cm/s为例，选取墙前水位下降某时刻时导出墙后计算截面的孔隙水压如图6所示。由孔隙水压的分布图得出：在瞬态渗流中孔隙水压的分布已不再是线性分布，并且孔隙水压也不等于静水压力。而图中墙高在0.5 m附近出现明显拐点是因为墙踵加设悬臂(长0.6 m)的影响，墙踵悬臂及铺设在悬臂板上的土工布也影响到该部分渗流线，对其他参数(不同降水速度和墙后填土渗透系数)情况也有类似结论。

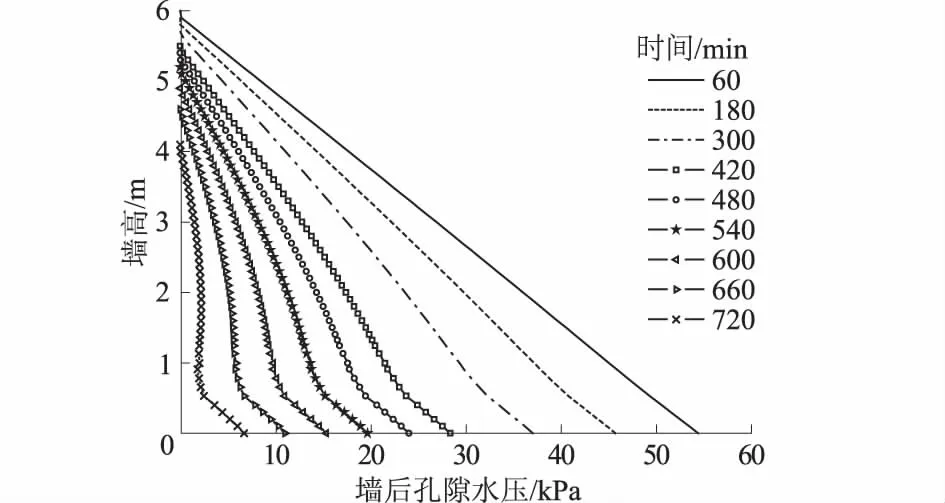
图6 墙后孔隙水压力分布Fig.6 Distributions of pore water pressure at the back of caisson wall against height

水土压力计算时：墙后水压力，根据瞬态渗流分析中孔隙水压力的分布特点，对孔隙水压力分布曲线进行分段拟合求积分，计算墙后水压力合力及作用点；墙前水压按静水压力计算；墙后主动土压力考虑回填砂土孔隙水压的作用，利用总应力减去对应时刻的孔隙水压。根据郎肯土压力理论，假定浸润线以上为非饱和土，浸润线以下为饱和土，其墙后主动土压力计算公式如下。

非饱和区：

σ1=γ1h1Ka；

(3)

饱和区：

σi=(γ1h1+γsathi-u)Ka。

(4)

式中：γ1为非饱和土重度,γ1=18 kN/m3；h1为非饱和土高度；γsat为饱和土重度,γsat=19.3 kN/m3；hi为距离浸润线的高度；Ka为主动土压力系数，Ka=tan2(45°-φ/2)；φ=32°为有效应力指标；u为对应时刻的孔隙水压力。

3.4 不同参数下岸墙稳定性分析

3.4.1 降水速度对岸墙稳定性影响

根据前面的分析，墙后填土渗透系数分别为4.0×10-4cm/s和3.8×10-3cm/s。结合式(1)—式(4)及墙前、墙后水压力的计算方法对岸墙在文中假定的降水速度下进行稳定性分析，其结果如图7所示。

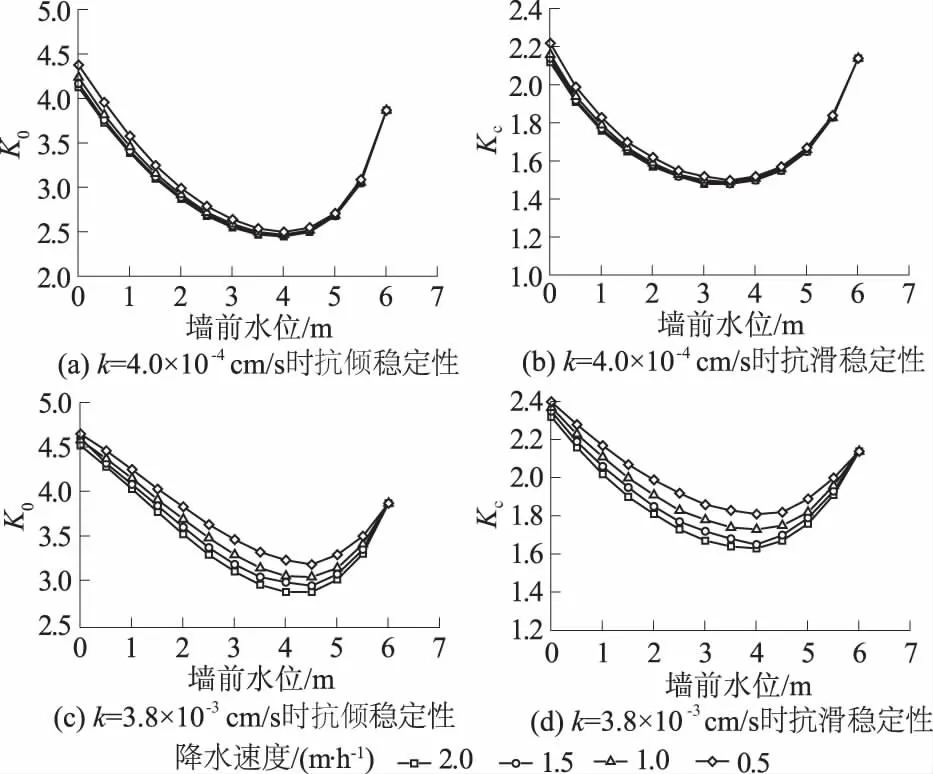
图7 不同降水速度下岸墙的抗倾、抗滑稳定性Fig.7 Stability of bankwall against overturning and sliding in the presence of different drawdown speeds

分析图7可得出：

(1)在所分析的范围内，填土的渗透系数较小时降水速度对岸墙抗倾、抗滑稳定性影响不大；填土的渗透系数较大时，降水速度对岸墙抗倾、抗滑稳定性影响较大；但在c,φ值不变情况下，填土渗透系数小的岸墙稳定性差。

(2)抗倾、抗滑稳定性都是随墙前水位的降低先减小再增大；在降水前期K0，Kc值减小得比较快，降水速度越大，降水前期安全系数值减小得越快；但同时随着墙前水位的下降，墙底扬压力减少，地基受到的承载力越来越大，地基安全性越来越小。

(3)在降水速度为0.5～2 m/h、墙后回填砂渗透系数为3.8×10-3cm/s时，抗倾稳定性最不利时刻出现在墙前水位处于2/3～3/4墙高之间；抗滑稳定性最不利时刻出现在墙前水位处于3/5～3/4墙高之间；随着降水速度的增大，岸墙抗倾、抗滑稳定性最不利时相应的墙前水位不断降低。

3.4.2 填土渗透性对岸墙稳定性影响

假定墙前降水速度为0.5 m/h，与3.4.1节计算方法相同对岸墙在文中假定的墙后填土渗透性下进行稳定性分析，其结果如图8所示。

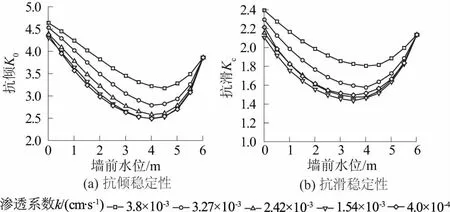
图8 不同墙后回填料渗透系数下岸墙的抗倾、抗滑稳定性Fig.8 Stability of bankwall against overturning and sliding in the presence of different backfill permeabilities

从图8可得出：

(1)在墙前降水速度一定时，对于墙后回填砂土而言，回填砂的渗透系数越大，岸墙稳定性越好；当渗透系数降到一定值后，渗透系数值的改变对岸墙稳定性影响不大。

(2)当降水速度为0.5 m/h时，岸墙在墙后回填料不同渗透系数下抗倾稳定性最不利时刻出现在墙前水位处于2/3～3/4墙高之间；抗滑稳定性最不利时刻出现在墙前水位处于3/5～3/4墙高之间；随着墙后回填料渗透系数的变小，岸墙抗倾、抗滑稳定性最不利时相应的墙前水位不断降低。

从图8(b)可看到，在墙前水位降落幅度一样情况下，墙后回填料的渗透系数k值从3.8×10-3cm/s递减到1.54×10-3cm/s时，Kc值随着k值的减小而变小；但当k=4×10-4cm/s时，在墙前水位降落幅度一样情况下，Kc值反而比k=1.54×10-3,2.42×10-3cm/s时大。

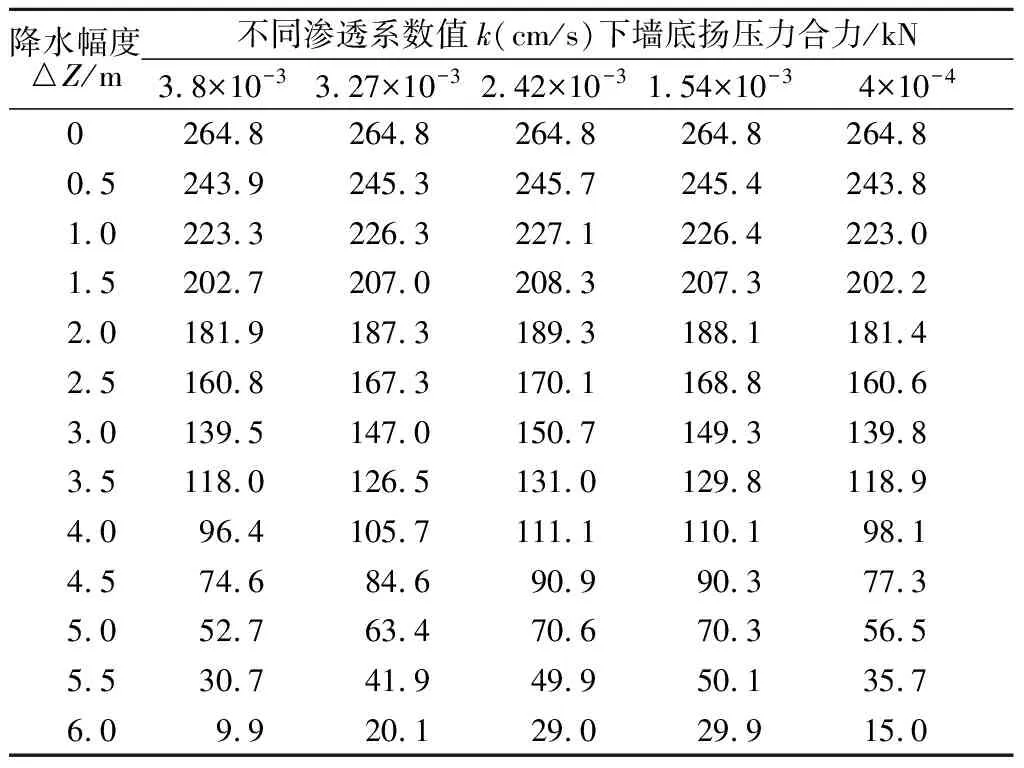
为什么当墙后回填料的渗透系数k值减小到一定数值后Kc值反而变大？通过分析不同墙前降水幅度△Z(m)时墙后回填料不同渗透系数值k(cm/s)相应的墙底扬压力合力U(表4)和墙后水压力合力Pw(表5)可发现：在墙前水位降落幅度一样情况下，墙底扬压力合力U和墙后水压力合力Pw随着墙后回填料渗透系数值的减小先增大后减小，k=1.54×10-3cm/s时大多数U值比k=2.42×10-3cm/s时的U值略小，k=4×10-4cm/s时的U值比k=2.42×10-3cm/s时的U值则小得多；k=4×10-4cm/s时的Pw值与k=2.42×10-3cm/s时的Pw值差别不大，但比k=1.54×10-3cm/s时的Pw值小得多，而且两者的Pw差值随着墙前降水幅度的增大而增大。这与墙踵悬臂及铺设在悬臂板上的强透水性的土工布的影响有关，也与砾石地基的强透水性有关。

此外，在各种条件下的岸墙稳定性最不利时刻的K0，Kc值均比设计骤降工况计算得到的K0，Kc值大，说明以往设计骤降工况的假定(墙前水位从墙顶骤降1 m，墙后水位与墙顶齐平)对于本文研究案例而言是偏于保守的。

表4不同墙前降水幅度时的墙底扬压力合力
Table4Resultanthydraulicupliftforcesatthewallbasewithdifferentdrawdownratesofwater
Table

降水幅度△Z/m不同渗透系数值k(cm/s)下墙底扬压力合力/kN3.8×10-33.27×10-32.42×10-31.54×10-34×10-40264.8264.8264.8264.8264.80.5243.9245.3245.7245.4243.81.0223.3226.3227.1226.4223.01.5202.7207.0208.3207.3202.22.0181.9187.3189.3188.1181.42.5160.8167.3170.1168.8160.63.0139.5147.0150.7149.3139.83.5118.0126.5131.0129.8118.94.096.4105.7111.1110.198.14.574.684.690.990.377.35.052.763.470.670.356.55.530.741.949.950.135.76.09.920.129.029.915.0

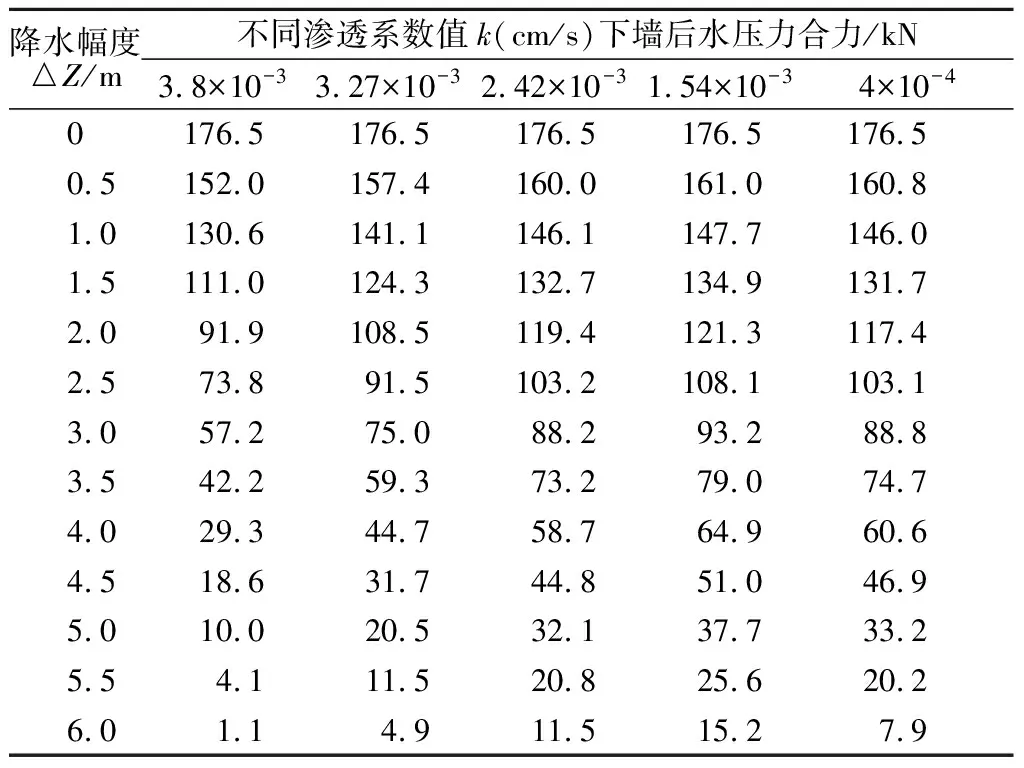
表5不同墙前降水幅度时的墙后水压力合力
Table5Resultantwaterloadsatthebackofcaissonwallwithdifferentdrawdownratesofwater
Table

降水幅度△Z/m不同渗透系数值k(cm/s)下墙后水压力合力/kN3.8×10-33.27×10-32.42×10-31.54×10-34×10-40176.5176.5176.5176.5176.50.5152.0157.4160.0161.0160.81.0130.6141.1146.1147.7146.01.5111.0124.3132.7134.9131.72.091.9108.5119.4121.3117.42.573.891.5103.2108.1103.13.057.275.088.293.288.83.542.259.373.279.074.74.029.344.758.764.960.64.518.631.744.851.046.95.010.020.532.137.733.25.54.111.520.825.620.26.01.14.911.515.27.9

3.5 墙前、墙后水位关系与最不利时刻关系研究

在第3.4节的研究中指出不同降水速度、不同墙后填土渗透系数下岸墙稳定最不利时刻发生在墙前水位下降1/4～2/5高度范围内。稳定分析表明，随着墙前水位的下降，墙后浸润线位置在不断发生变化，墙前、墙后水土压力也在不断改变，当水土压力变化到某一数值时，岸墙处于最不利时刻。

文中以墙后计算截面处不同时刻浸润线位置为墙后水位高度，以此来分析河道水位降落过程中墙前、墙后水位关系，并研究其与岸墙最不利时刻之间的关系。图9(a)反映墙后填土渗透系数为4×10-4cm/s时不同降水速度情况下墙前、墙后水位差的变化曲线；图9(b)反映在降水速度0.5 m/h情况下不同墙后填土渗透系数时的墙前、墙后水位差的变化曲线。

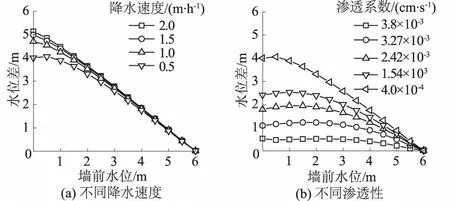
图9 不同参数下墙前、墙后水位差的变化曲线Fig.9 Variation of water level difference in front of and at the back of caisson wall with different parameters

在墙前水位降落到同一高度时，由图9(a)可看到，在墙后回填料渗透系数不变情况下，墙前、墙后水位差随着降水速度增大而增大，最大水位差出现于墙前水位基本降落到达墙底时；由图9(b)可知，对同一降水过程，墙前、墙后水位差随着墙后回填料渗透系数的变小而增大，且最大水位差出现时间随着渗透系数的变小而滞后。比较图9中(a)和(b)可知，墙后填土渗透性对墙前、墙后水位差的影响较降水速度大。

比较图8和图9(b)，发现岸墙最危险时刻并不是发生在墙前、墙后水位差最大的时刻(在本文研究的案例中，岸墙稳定性最不利时刻为墙前水位处于3/5～3/4墙高之间，而墙前、墙后水位差最大一般出现在墙前水位处于1/2墙高以下)。因为影响挡土墙稳定性的是墙后水土压力的大小及墙体的有效重力(考虑浮力/扬压力影响)，而不是单独的水位变化。随着墙前水位的变化，墙后水土压力及墙体的有效重量也在随之变化，故不能单纯认为水位差越大，岸墙越不稳定。

4 结 论

本文通过大型模型试验对Seep/w渗流软件进行标定，以此为理论依据分析了不同降水速度、不同墙后填土渗透性对挡土墙抗倾、抗滑稳定性影响规律及墙前、墙后水位关系与岸墙稳定最不利时刻的关系，得到如下结论：

(1)由试验与数值模拟对比可知，在保证试验参数可靠的情况下，Seep/w可以较准确反映挡土墙墙后水位的变化。

(2)随着墙前水位的骤降，墙后水压力呈非线性分布，而且岸墙的稳定性均先下降再升高。

(3)在文中所研究的范围内，墙后填土渗透性对墙前、墙后水位差及岸墙稳定性的影响均较降水速度大；回填土渗透系数越大，墙前、墙后水位差越小，岸墙稳定性越好。

(4)挡土墙的稳定性是由墙前、墙后水土压力及墙体的有效重力共同作用下决定的，墙前、墙后水位差最大的时刻并不一定是挡土墙稳定性最差的时刻。