土工袋挡墙变形特性有限元分析

，，，

(河海大学 水利水电学院，南京 210098)

1 研究背景

土工袋因其制作简单、 取材方便、 成本低廉等优点， 已经被广泛应用于地基加固、 减震隔震、 膨胀土处理以及各类工程的支挡结构， 并取得了极为广泛的经济效益。 近年来， 董鹏等[1]、 刘斯宏等[2]、 Matsuoka等[3]对土工袋增强机理、 工程特性等进行了较为深入的研究， 在此基础上将土工袋直接应用于构筑挡土墙。 土工袋挡墙作为一种新型加筋土结构， 对墙后填土兼有原位挡墙和表面压重的作用， 且与传统重力式挡墙相比， 土工袋结构较轻， 降低了对地基承载力的要求。 同时， 土工袋内填充物可以是现场开挖土料， 也可以是工程弃土、 建筑废料， 很好地解决了废料处理的问题； 在袋装土内放入草种， 还可起到绿化墙面、 美化环境的作用。 目前， 土工袋挡墙的应用在国内外的工程中已愈加广泛。

目前对土工袋及其组合体的研究已取得一定的成果。 刘斯宏等[4-6]研究了影响土工袋堆叠体层间摩擦大小的因素， 通过室内模型试验测量直立挡墙墙后填土的位移模式及墙背土压力的大小， 用薄层单元法推导了墙背土压力的计算公式， 并通过小型振动台试验探究了土工袋挡墙的动力特性； 王艳巧等[7]通过室内模型试验探究了土工袋堆叠体对砂性土质边坡的加固效果； 文华等[8]针对建渣土工袋倾斜挡墙的破坏形式和墙面变形特性特征进行了室内模型试验； Tantono 等[9]和高军军等[10]利用有限元法， 用理想弹塑性的杆单元模拟编织袋， 研究了二维模型竖向荷载下单个袋体的变形规律； Yousef等[11]和李栋等[12]通过建立三维有限元模型， 模拟了单个袋体的无侧限压缩试验， 但对于土工袋支挡结构的建模则多是对单个袋体附加黏聚力[13-15]。 上述试验成果均没有对土工袋挡墙在不同工况下的变形特性进行系统深入的探究， 在推导土压力计算公式时也未考虑挡墙变形的影响， 而实际墙后土压力的分布与挡墙变形模式密切相关。 因此， 土工袋挡墙的设计仍处于经验阶段， 土压力计算方法也缺少合理的理论基础。

针对土工袋挡墙应用范围较广， 各种工况对土工袋挡墙变形特性的影响不便通过模型试验获得的问题， 本文运用岩土工程通用有限元分析计算软件GTS对土工袋挡墙进行模拟。 GTS是针对岩土及隧道工程的分析与设计而开发的有限元计算软件， 具有14种材料本构模型及用户自定义本构， 前后处理功能强大， 能反映大部分岩土体的变形及破坏模式。 本文通过其施工阶段模块对挡墙初始堆筑阶段由于自重引起的变形进行清零， 重点探究挡墙变形形态和墙面水平位移大小随挡墙坡度、 高宽比及墙后填土表面荷载强度的变化规律， 并与已有试验结果[5,8]进行对比。 计算结果对工程设计具有一定的参考意义， 为土压力计算方法提供理论基础。

2 土工袋挡墙的模拟

2.1 编织袋的模拟

土工袋作为土工织物的一种，具有抗拉，但不能抗压、弯、剪的普遍特性，因此可以采用线弹性的杆单元对编织袋进行模拟。已有研究成果[10]表明，杆单元不仅能模拟编织袋对袋内土体的约束作用，同时能够客观地反映土工袋的应力-应变关系，将其用于模拟土工袋挡墙可以更加准确地反映出墙内不同位置处土工袋的变形。其不足之处在于实际的编织袋在其经纬向均对袋内土体有约束作用，而非单向约束，但由于挡墙产生主要由于墙后水平土压力的作用，因此袋体本身的变形较小，且计算结果中去除了初始堆筑阶段自重引起的墙体变形，因此运用杆单元法能够获得较为合理的挡墙变形结果。

为使计算结果合理，建模时需设置杆单元属性仅受拉，允许压力为0，避免计算过程中出现受压杆单元，影响计算结果准确性。

2.2 接触面的模拟

本文采用Goodman无厚度接触单元进行模拟。Goodman单元可以较好地模拟接触面上的错动滑移或张开，同时还可以考虑接触面变形的非线性特性。由于其单元厚度为0，当应力较大时，有时会出现两侧单元重叠，因此一般在受压时采用较大的法向刚度模量；由于接触面不能承受拉应力，当接触面受拉时，法向刚度模量取较小值。接触面受压法向刚度模量通常可取为(50～100)Emin[16](Emin为相邻材料的弹性模量较小值)，本文中取受压法向刚度模量kn=50Emin。

土工袋挡墙中存在3种形式的接触面：袋子与袋子之间、袋子与袋内土体之间以及袋子与墙后填土之间的接触。假设袋内材料颗粒与编织袋之间不发生相对滑动，仅在编织袋之间和挡墙与填土之间设置接触单元。

3 计算模型及参数

袋内填充料与墙后填土均为河砂，采用Duncan-Chang非线性弹性本构模型。参考文献[7]和文献[17]、文献[18]，本文计算中砂土模型参数为：弹性模量E=20 MPa，重度γ=17.5 kN/m3，黏聚力c=3.25 kPa，内摩擦角φ=30°，初始加载模量系数K=600，指数n=0.6，破坏比Rf=0.8，体积模量系数Kb=200，体积模量指数m=0.15。参考编织袋物理力学参数[10]所用杆单元参数如下：重度3.3 kN/m3，矩形截面宽度1 m，高度3×10-4m，弹性模量为5 GPa。根据土工袋层间摩擦试验[4]中所得河砂袋的层间摩擦系数，确定接触面参数如下：受压法向刚度模量kn=106kN/m3，切向刚度模量ks=104kN/m3，库伦摩擦参数中黏聚力取3.25 kPa，摩擦角取25°。

根据某实际工程情况设定模型参数，即墙高为5 m，袋体尺寸主要为1 m×1 m×0.25 m(长×宽×高)，墙后填土均布荷载施加范围取为6 m。挡墙由土工袋交错布置、垂直堆放而成，交错层两侧用相应尺寸的小袋子进行填补。假设墙体足够长，按平面应变问题处理。为精确计算结果，土工袋单元尺寸设置为0.1 m，墙后填土单元尺寸设置为0.2 m，采用德劳内网格。计算时限制最下层土工袋的水平向和竖向位移，模型底部和右侧均固接。

本文分别建立了不同高宽比、不同坡度和不同荷载强度下土工袋柔性挡土墙的计算模型，以探究各个因素对挡墙变形特性影响的大小与方式。计算模型及有限元网格划分如图1所示。

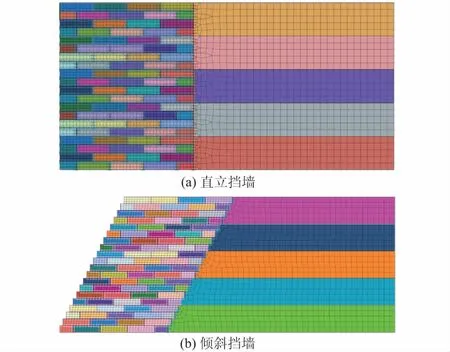
图1 有限元网格划分示意图Fig.1 Sketch of partitioning of finite element meshes

4 计算结果

4.1 坡度对土工袋柔性挡土墙变形规律的影响

图2给出了挡墙承受荷载为10 kPa和50 kPa、高宽比H/B分别为5∶4，5∶3，5∶2时，不同填土坡度土工袋挡墙变形特性的影响。

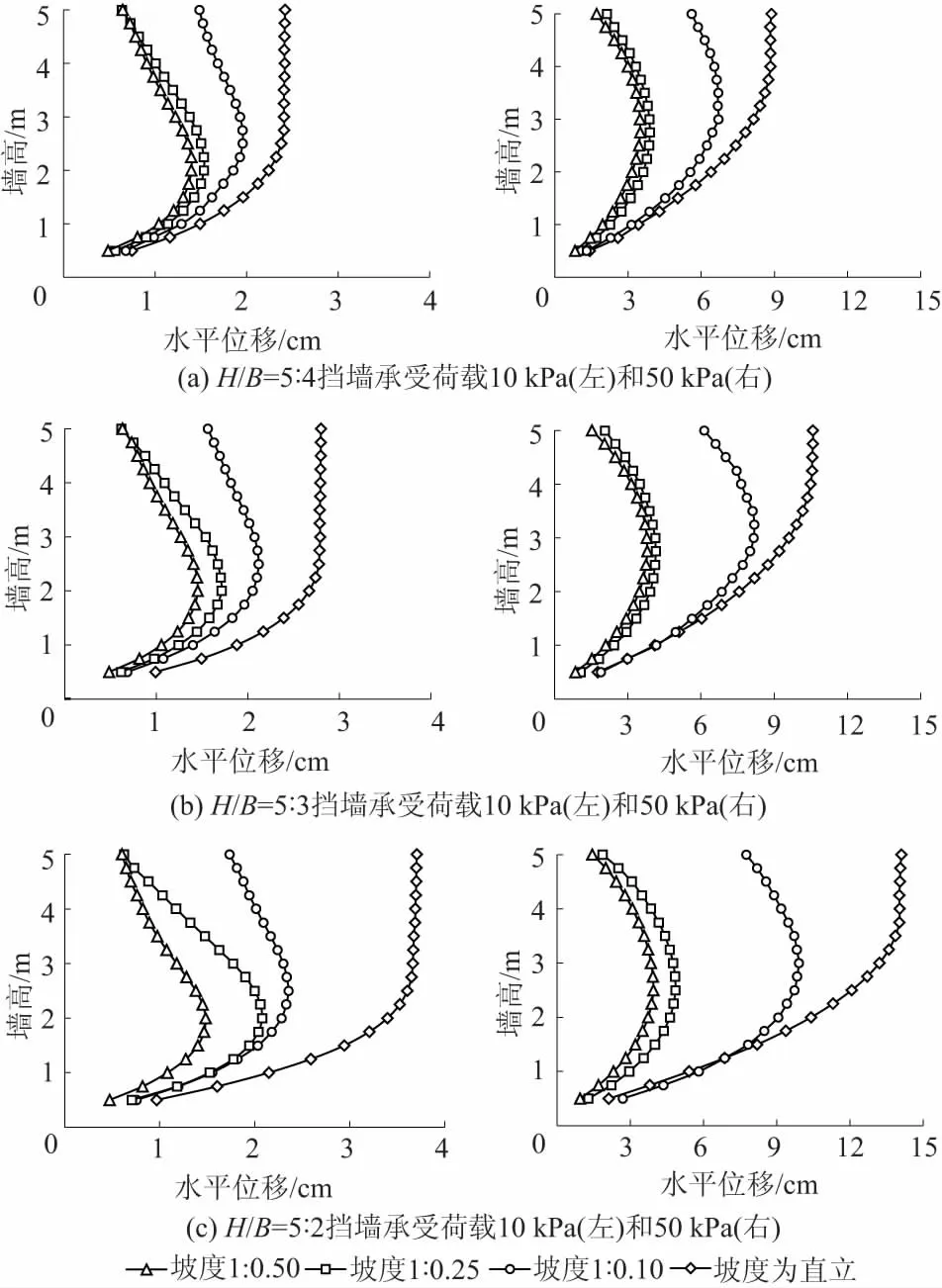
图2 坡度对于土工袋挡墙水平位移的影响Fig.2 Effect of slope gradient on horizontal displacement of retaining wall constructed with geobags

从图2中可以看出，坡度直接决定了土工袋挡墙的变形形态。挡墙直立时，挡墙发生“上平下转”的变位模式：最大位移发生在挡墙顶部，上部某一高度内墙面水平位移沿高程基本不变，近似平动，随着高度的降低，墙面水平位移逐渐减小，近似转动；随着坡度的减小，挡墙顶部水平位移量迅速减小，挡墙底部水平位移量仍然较小，最大位移发生点逐渐下移，形成“中间大两端小”的鼓形变位模式。可见减缓坡度可有效地限制墙顶过大的水平位移，这是由于直立挡墙墙后填土的位移模式主要为向前倾覆[2]，在墙后填土的推动下，墙身向前倾覆，而上部挡墙所受土压力较小，墙体变形主要以单个袋体变形为主而不发生层间滑动，因此出现“上部平动，下部转动” 的位移模式，挡墙顶部水平位移较大；坡度变小后，挡墙下部三角形土体范围变大，这部分土体由于缺少编织袋的加筋作用，顶部沉降过大，随着深度的增加沉降减小，墙后填土的位移模式主要为沿剪切带滑坡[5]，因此挡墙顶部以竖向位移为主，水平位移量较小，而挡墙中下部所受土压力较大，中下部位移仍然较大。同时，随着坡度的减小，挡墙自身重力发挥的压坡作用越大，墙面各高程处水平位移量均有所减小。

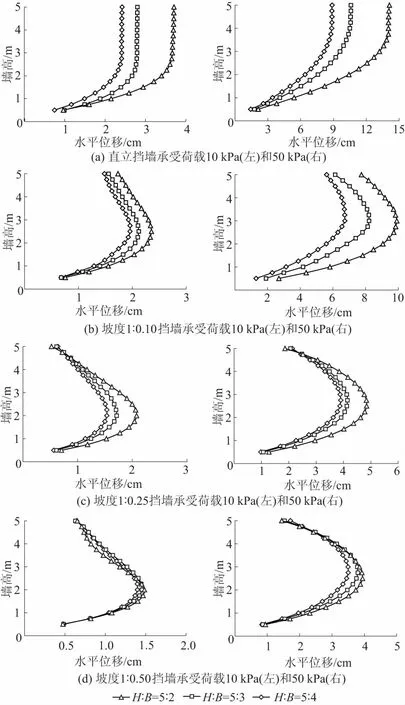
图3 高宽比对于土工袋挡墙水平位移的影响Fig.3 Effect of height-width ratio on horizontal displacement of retaining wall constructed with geobags

4.2 高宽比对土工袋柔性挡土墙变形规律的影响

为了研究土工袋柔性挡土墙的高宽比H/B对其变形特性的影响，对同一高度下不同宽度的土工袋挡墙分别进行有限元分析。图3给出了挡墙铅直以及坡度分别为1∶0.10，1∶0.25，1∶0.50、荷载为10 kPa和50 kPa时不同高宽比下挡墙受力变形产生的墙体前端的水平位移量。从图3中可以看出，当高宽比H/B较大时，挡墙刚度较小，墙体内部易发生层间滑动，具体表现为墙面弯曲变形较大；随着挡墙宽度增加，高宽比H/B逐渐减小，挡墙的整体刚度变大，挡墙变形形态保持不变，墙面弯曲变形逐渐减小，但墙底水平位移基本不变。对于坡度较陡的挡墙(坡比≥1∶0.10)，高宽比不仅可以减小墙面的弯曲变形，还能适当限制挡墙顶部的水平位移，而对于坡比≤1∶0.25的挡墙，高宽比对挡墙顶部水平位移影响很小。由此可见，对于公路等坡度较缓的挡墙，可考虑从上而下墙宽逐渐增大的断面型式以减小工程量和造价。此外，通过对比不同坡度挡墙增大高宽比对其减小水平位移量的效果可得，坡度越小，高宽比对挡墙变形量的影响越小，这是由于坡度变小后，墙身刚度的作用减小，挡墙自重对填土的压坡作用变大。

4.3 填土表面荷载强度对土工袋柔性挡土墙变形规律的影响

图4给出了直立和坡度1∶0.50两种挡墙在高宽比H/B分别为5∶4，5∶3，5∶2时，填土表面逐级施加10，20，30，40，50 kPa荷载后挡墙前端的水平位移。从图4中可以看出，填土表面荷载强度不能改变挡墙的变形形态，对于同一高宽比挡墙，填土表面承受荷载越大，墙背所受墙后土压力越大，墙面弯曲变形越大，墙底水平位移基本不变。通过对比发现，随着荷载增大，直立挡墙顶部水平位移变化较大，而倾斜挡墙顶部水平位移增大值较小。

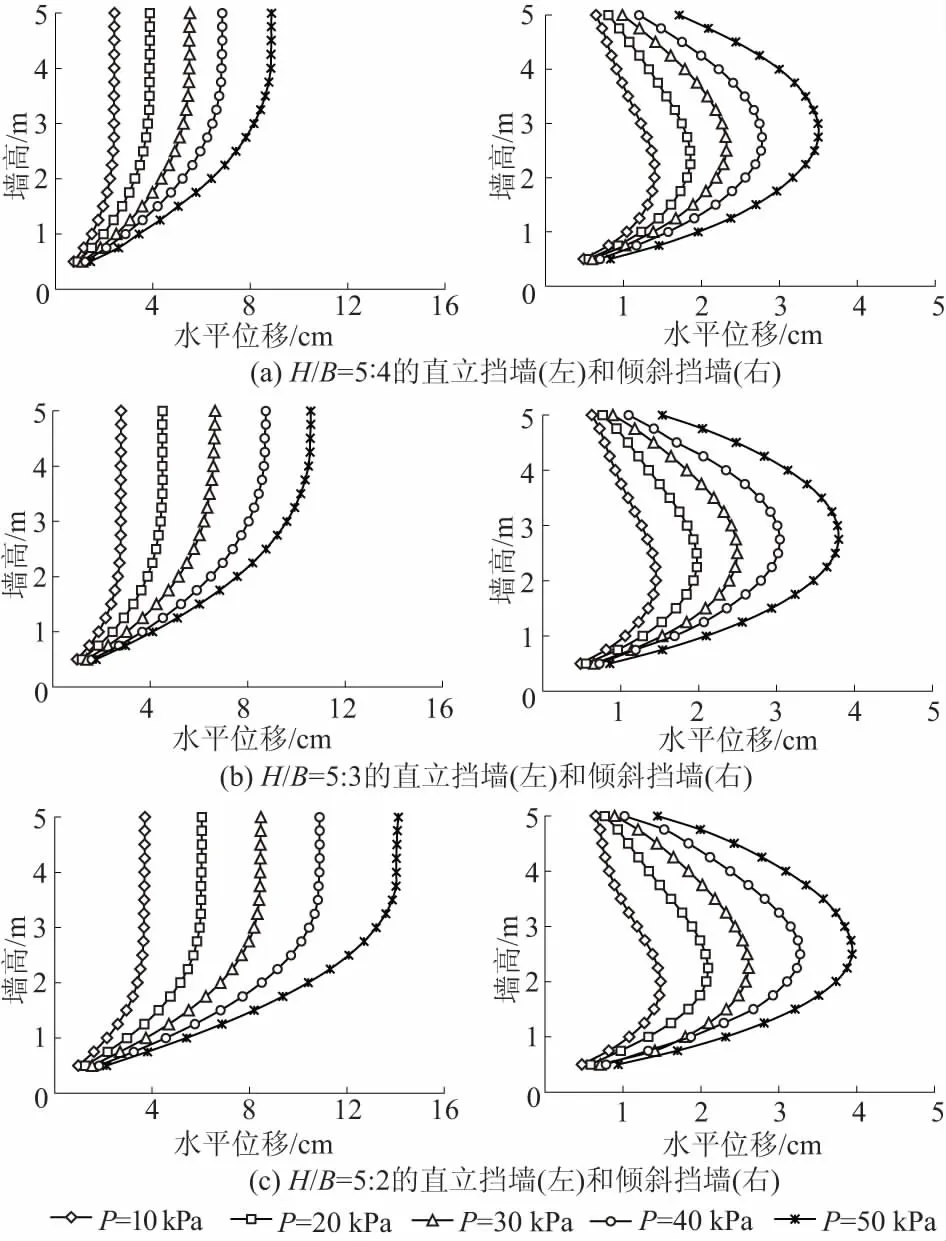
图4 荷载强度对于土工袋挡墙水平位移的影响Fig.4 Effect of surface load on horizontal displacement of retaining wall constructed with geobags

此外，由上述分析可以发现，土工袋挡墙在直立和倾斜时产生了2种不同的位移模式，且两者中均存在关键的转折点。直立挡墙上部平动部分水平位移量与转折点处位移量基本相等，下部转动区水平位移量由墙底向上逐渐增大，在转折点处达到最大值；倾斜挡墙在转折点处发生最大位移，挡墙变形由转折点向墙顶和墙底逐渐减小。因此减小转折点处的挡墙水平位移量是限制土工袋挡墙变形的关键。为进一步探究转折点位置变化范围及其影响因素，直立挡墙中以相邻节点位移差值开始小于挡墙最大位移的1%的点为转折点，倾斜挡墙中以位移最大点为转折点，将图4中不同工况下转折点位置高程提取，绘制成曲线，如图5所示。从图5中可以看出，填土表面荷载强度越大，转折点位置越高。根据这一规律，得出各个坡度挡墙变形转折点的变化范围，见表1。直立挡墙转折点位置主要在挡墙中上部(1/2～4/5)H范围内变化，而坡度<1∶0.25的倾斜挡墙转折点位置基本保持在挡墙中下部(2/5～1/2)H。

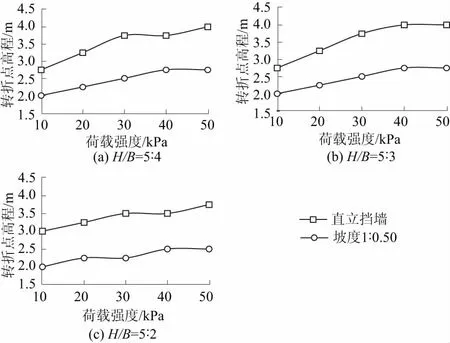
图5 荷载强度对于土工袋挡墙变形转折点位置的影响Fig.5 Effect of surface load on the height range of turning point of the deformation curve of retaining wall constructed with geobags

坡度高度坡度高度直立(1/2～4/5)H1∶0.25(2/5～1/2)H1∶0.10(1/2～3/5)H1∶0.50(2/5～1/2)H

5 结 论

通过岩土工程有限元分析软件GTS研究了土工袋挡墙在高宽比、坡度及填土表面荷载强度等不同组合工况下的变形规律，主要结论如下：

(1)土工袋挡墙高宽比、坡度以及填土表面荷载强度对于挡墙变形特性具有重要影响。

(2)坡度直接决定土工袋挡墙变形形态，直立挡墙发生近似“上部平动、下部转动”的位移模式，最大位移发生在挡墙顶部；随着坡度变小，挡墙顶端水平位移迅速减小，最大位移发生点逐渐下移，最大水平位移变小，墙身变形呈现“中间大两端小”的鼓形变位。

(3)同一高度挡墙在相同荷载作用下，高宽比H/B越小，墙面变形量越小，但高宽比的改变并不能改变挡墙变形形态；对于坡度较大的挡墙(坡度≥1∶0.10)，减小高宽比可以限制挡墙顶部的水平位移，而对于坡度≤1∶0.25的挡墙作用很小；挡墙坡度越大，减小高宽比对限制墙面弯曲变形的效果越好。

(4)填土表面荷载强度越大，墙面弯曲变形越大，挡墙变形形态不变；直立挡墙顶部水平位移受荷载大小影响相对倾斜挡墙较大；墙面变形转折点位置随着填土表面荷载的增大逐渐上移，直立挡墙转折点在挡墙中上部(1/2～4/5)H范围内变化，而坡度<1∶0.25的倾斜挡墙转折点位置基本保持在挡墙中下部(2/5～1/2)H。