U形和弧形底梯形渠道衬砌冻胀力的统一解

，*，，

(1.宁夏大学土木与水利工程学院， 宁夏银川750021；2.宁夏节水灌溉与水资源调控工程技术研究中心， 宁夏银川750021；3.旱区现代农业水资源高效利用教育部工程研究中心， 宁夏银川750021)

0 引言

宁夏引黄灌区年引水量达70余亿m3，但存在大量的渠水渗漏，渠道水利用系数仅为0.48，水资源浪费严重。为节约用水，减少灌渠渗漏，必须进行渠道防渗衬砌。目前，一般利用混凝土板、塑膜或两者结合进行渠道防渗，可减少渗漏70 %～90 %[1]。整体U形混凝土衬砌因其自身抗冻能力强而在宁夏引黄灌区渠道斗渠和支渠防渗衬砌中得到广泛应用，但宁夏处于典型的季冻区，冬季昼夜温差可达15 ℃以上，地基易冻胀而导致整体U形混凝土衬砌板的冻胀破坏，因此，准确计算整体U形渠道冻胀内力尤为重要。

国内研究混凝土衬砌渠道冻胀成果较多。力学模型分析研究成果：王正中等[2]考虑法向冻胀力、切向冻结力和衬砌板自重力三种荷载作用，建立了弧形底梯形渠道砼衬砌冻胀破坏的静力学分析模型。王正中[3]考虑法向冻胀力、法向冻结力、切向冻结力和衬砌板自重力4种荷载作用，建立了梯形渠道坡板的简支梁计算模型，得出了最大弯矩计算公式及混凝土板的强度校核公式。石娇等[4]和孙杲辰等[5]利用弹性力学理论，建立了弧底梯形和梯形混凝土衬砌渠道冻胀断裂破坏力学模型，给出了渠道衬砌设计方法。张茹等[6]建立了U 形混凝土衬砌渠道非对称冻胀破坏的力学模型，分析了渠道衬砌结构的冻胀内力。李翠玲等[7-8]考虑法向冻胀力、法向冻结力、切向冻结力和重力的共同作用下，分别建立了0倾角坡板的整体式U形混凝土衬砌渠道计算模型和两拼式U形渠道混凝土衬砌结构冻胀破坏力学模型，并给出了内力计算公式。郑源等[9]考虑复合土工膜和渠基土壤的摩擦力、冻胀力和冻结力的共同作用，建立了渠道板悬臂梁结构的计算模型，并求解了最大弯矩表达式。申向东等[10]建立了多跨简支梁坡道板的混凝土预制板衬砌的计算模型，利用平衡极限状态条件解出了梁的内力。肖旻等[11]通过对梯形渠道砼衬砌冻胀破坏力学的分析，认为渠道所受冻胀力和冻结力之间相互影响、相互依赖。

数值模拟分析研究成果：余书超等[12]建立渠道刚性衬砌受冻胀时的内力计算模型，并通过分析合理地解释了边坡板在实际工程中沿斜坡整体上移和隆起架空的现象。刘旭东等[13]和高靖等[14]利用ADINA数值模拟软件分别建立了“适变断面”混凝土衬砌渠道冻胀模型和不同U型结构混凝土渠道冻胀模型，刘旭东等的模拟得出边坡系数为1∶1.7～1∶1.4时，“适变断面”混凝土衬砌渠道的抗冻效果显著，高靖等的模拟得出坡道板倾角在8°～22°范围内，倾角的增大对其冻胀不均匀性影响适中的结论。安鹏等[15]和王英浩等[16]利用ANSYS 有限元软件分别建立了原渠道和部分保温渠道的热力耦合模型以及玻璃钢渠道的温度场、位移场模型。安鹏等的数值模拟得出部分保温法可大幅削减渠道的冻胀量和冻胀力，阴坡削减可达80 %以上，王英浩等的研究表明，玻璃钢渠道的抗冻能力优于混凝土渠道。董江伟等[17]和李爽等[18]利用限元分析软件 ABAQUS分别建立了典型的引额济克的梯形渠道接触特性模型和混凝土衬砌板与冻土接触非线性的渠道冻胀模型，董江伟等的研究表明，最大位移和应力变形发生在渠道坡板与底板交界处，说明在交界产生应力集中现象。李爽等认为考虑接触非线性的数值模型更能反映衬砌渠道冻胀破坏过程。

Everett[19]根据毛细理论分别对冻胀和冻胀力进行定量的解释和估计，毛细理论被称为第一冻胀理论。Miller[20-21]提出第二冻胀理论。Arenson[23]等研究了冻土流变特性与温度、含冰量、围压和荷载历史等条件之间的关系模型。

依据渠道防渗工程技术规范(GB/T 50600—2010)中的规定和说明可知，整体式U形渠道衬砌和弧形底梯形渠道衬砌结构构成相似，但其边坡系数、断面尺寸和渠道等级不同，U形整体式渠道衬砌边坡系数范围为0～0.4(相当于坡板倾角为0°～21.8°)，弧形底梯形渠道衬砌边坡系数范围为0.5～2.0(相当于坡板倾角为26.6°～63.4°)；整体式U形渠道衬砌断面小于弧形底梯形渠道衬砌；U形整体式渠道衬砌为五级衬砌，弧形底梯形渠道衬砌为四级以上衬砌。

前人研究的冻胀内力模型绝大数为静定结构，但整体式渠道冻胀模型实际上应为超静定结构，而利用静定计算简图计算整体式渠道衬砌内力会导致计算结果和实际误差较大，同时超静定结构冻胀位移也会产生较大的附加应力，因此，将超静定结构简化为静定结构显然有不妥之处。李翠玲[7]等建立0倾角坡板的整体式U形混凝土衬砌渠道超静定计算模型，但没有考虑坡板倾角的变化对渠道冻胀内力的影响。本研究建立了整体U形和弧形底梯形砼渠道冻胀内力的统一计算模型，研究不同坡板倾角、不同板厚、不同坡板长和不同半径对整体式U形和弧形底梯形混凝土渠道衬砌内力的影响规律，旨在为整体U形和弧形底梯形砼渠道防冻胀设计提供理论依据。

1 渠道砼衬砌冻胀内力计算简图及求解

渠道冻胀力学模型建立的方法和步骤：先假定渠道受力的数量和性质，建立力学计算简图，然后依据经验公式计算切向冻结力，并列出平衡方程，解出其余未知力。

1.1 基本假定

①渠道衬砌混凝土为均质、各向同性的线弹性材料。②渠道衬砌结构变形为小变形。③法向冻结力作用点位于坡板顶部，作用线垂直于坡道板，并假定坡顶变形为0[3]。④法向冻胀力由坡板顶部沿坡板到坡板底部呈线性变化分布，坡顶为0，坡底最大，渠底均匀分布，其值等于坡底法向冻胀力[3]。⑤切向冻结力由坡板顶部沿坡板到坡道板底部线性变化分布，坡顶为0，坡底最大，由渠底板与坡板连接处的最大连续减小到底板中心处为0[3]。⑥渠道衬砌板的周边土均已完成冻结，只考虑冻胀力和渠道自重对衬砌结构的作用，忽略土压力对渠道的作用[3]。⑦水平夹角α为坡板与水平线的夹角，弧形底板的中心角为2α，水平倾角与坡板倾角之和为90°。

1.2 渠道砼衬砌冻胀内力的计算简图求解

根据基本假定可以建立图1和图2的渠道冻胀内力计算简图。图中计算半径R为圆心到衬砌板轴线的距离，渠道防渗工程技术规范(GB/T 50600—2010)的半径为圆心到衬砌板内表面的距离，利用规范对计算半径取值时，计算半径R等于规范半径加上1/2衬砌板厚。

图1和图2中，渠道衬砌的自重为已知量，切向冻结力可由经验公式(1)计算[3]，即：

τ=c+mt,

(1)

式中：t为负温绝对值，m为与土质有关系数(c=0.3～0.6 kPa，m=0.4～1.5 kPa/℃)。

图1法向冻结力及法向冻胀力分布图的计算简图
Fig.1Calculatingdiagramofnormalfreezingandfrost-heaveforces

图2切向冻结力分布图的计算简图
Fig.2Calculatingdiagramofdistributionmapwithrespecttotangentialfreezingforces

在力学计算图中，法向冻结力F和法向冻胀力q为未知力，要计算出这两个未知力，需要两个方程去求解，由图1和图2可知，法向冻结力合力、法向冻胀力合力的作用线与计算简图的纵向对称轴重合，故只能列出1个静力学平衡方程，见式(2)。

2Fcosα+qlcosα+2qRsinα=τlsinα+τR(1-cosα)+2bγ(l+Rα),

(2)

式中：l为坡板长，b为板厚，γ为混凝土的重度。

图3 坡板计算简图Fig.3 Calculating diagram of slope roof

要解出2个未知力，必须引入1个变形协调方程才能求解这2个未知力。以坡板的计算简图为例(图3)，假设坡板底部为固定端支座的悬臂梁。依据基本假定②可知，简支梁自由端的竖向变形为自重力、法向冻胀力、法向冻结力和切向冻结力等4种荷载共同作用所产生的变形的叠加(小变形假设)，依据基本假定③，可列出变形协调方程，然后，可由联立方程组解出法向冻结力和法向冻胀力。

四种荷载独立作用下的挠曲线方程可由积分法算出。

法向冻胀力作用的挠曲线方程为：

(3)

切向冻结力作用的挠曲线方程为：

(4)

法向冻结力作用的挠曲线方程为：

(5)

自重垂直于坡板作用的挠曲线方程为：

(6)

令公式(3)～(6)中的x=l，可计算出板自由端的位移，依据假设，坡板顶端的位移为零，则变形协调方程为：

(7)

联立方程(2)和式(7)，可解出q和F：

(8)

(9)

四种荷载作用下的总弯矩方程为：

(10)

为了计算出弯矩的极值，对公式(10)求导，即可求出最大弯矩的作用位置，即：

(11)

把公式(11)的值代入公式(10)即可算出Mmax，依据力学公式，可计算出坡板的最大拉应力为：

(12)

其中，

(13)

由力学理论可知，整体U形和弧形底梯形渠道衬砌的弧形底衬砌结构相当于一个反拱，属于一个偏心受压构件，其抵抗冻胀力的能力很强，一般不会发生破坏；另一方面，弧形底渠道衬砌冻胀内力计算模型可参考文献[2]中的计算方法，故本文在此没有进行弧底衬砌冻胀内力分析。

2 整体U形渠道冻胀内力的计算结果与分析

由公式(8)～(11)可知，渠道衬砌结构的冻胀内力与渠道衬砌板厚、坡板长、半径和坡板倾角等4因素有关，其计算公式为非线性方程，随着4因素的变化，坡板最大弯矩及最大弯矩发生的位置均会呈非线性的变化规律。为此，开展了上述4因素对渠道冻胀内力的影响规律等方面研究。在文中后面的分析过程中，为了简化表达，衬砌厚度简称为厚度，坡板长简称为板长，坡板倾角简称为倾角。

2.1 0°倾角、半径300 mm的整体U形砼衬砌的冻胀内力变化规律

依据规范渠道防渗工程技术规范(GB/T 50600—2010)，对于0°(边坡系数为0)倾角、半径300 mm的整体式砼衬砌渠道内力进行分析。依据规范说明，当渠道水流中含推移质较多且粒径较大时，板厚宜加厚10 %～20 %。宁夏黄灌区泥沙含量较高，渠道衬砌可加厚，故板厚可采用40～120 mm，板长可采用300～400 mm。

设黏聚力c=0.45 kPa，绝对负温值为-16 ℃，m=0.8 kPa/℃，利用公式(1)计算出τ=13.25 kPa。依据公式(8)～(13)可计算出不同板厚，不同板长渠道衬砌的法向冻胀力(q)、法向冻结力(F)、渠道衬砌内表面最大拉应力(σmax)和最大拉应力发生位置(用最大拉应力发生处距坡板顶距离与坡板的长度之百分比表示)，计算结果见表1和表2。

表1 板长300 mm的渠道衬砌冻胀内力Tab.1 Channel lining internal force of the slope at the length of 300 mm

注：表1中冻胀力和冻结力正号表示力的方向和计算简图中假设的方向一致，反之，方向相反；最大应力正号表示受拉，反之，表示受压。

表2 板长400 mm的渠道衬砌冻胀内力Tab.2 Channel lining internal force of the slope at the length of 400 mm

由表1、表2和图4～图7可知，法向冻胀力随着板厚的增加呈线性增加的趋势，即为渠道衬砌自重力与法向冻胀力呈正比例增加；衬砌内表面最大拉应力随着板厚的增加呈降低的趋势，说明渠道厚度的增加，有利于提高渠道的冻胀能力。在混凝土结构设计中，为了防止混凝土构件发生受拉破坏，一般要求混凝土构件内部不产生拉应力，或者产生拉应力很小(C15混凝土的拉应力约1 MPa，假定取其1/10界定为很小，即约为0.1 MPa)，依据此规则并结合表1和表2可知， 0°倾角、半径300 mm整体式U形砼衬砌渠道板长300 mm时，则以板厚4～6 cm较佳，板长400 mm时，则以板厚6～8 cm较佳。由混凝土构件内部不产生拉应力，或者产生拉应力很小的规则，可确定任意倾角、板长、温度、厚度和温度的整体式U形渠道的最佳厚度。板长300 mm衬砌的切向冻结力随着板厚的增加呈线性增加，而板长400 mm衬砌的切向冻结力随着板厚的增加呈线性减小。板长300 mm衬砌的最大拉应力发生在离坡板顶约43 %长度处，并随着厚度的增加，其位置有靠近坡底的趋势，板长400 mm衬砌的最大拉应力发生在离坡板顶约49 %长度处，并随着厚度的增加，其位置有远离坡底的趋势。

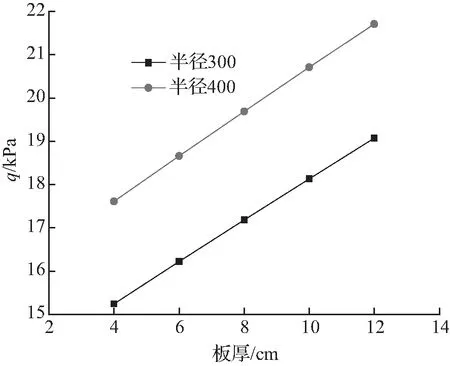
图4法向冻胀力与板长、板厚的关系
Fig.4Relationshipbetweenthenormalfrost-heaveforcesandthelengthofslope,thethicknessofplate

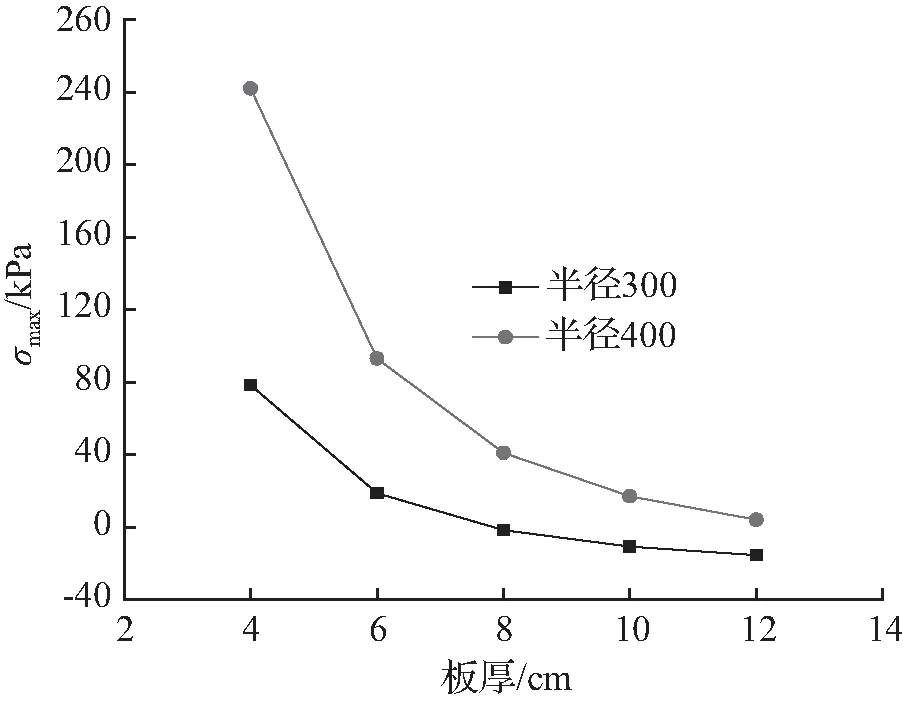
图5最大拉应力与板长、板厚的关系
Fig.5Relationshipbetweenthemaximumstressoflininginnersurfaceandthelengthofslope,thethicknessofplate

图6切向冻结力与板长、板厚的关系
Fig.6Relationshipbetweenthetangentialfreezingforceandthelengthofslope,thethicknessofplate

图7最大应力位置与板长、板厚的关系
Fig.7Relationshipbetweenthemaximumstressandthelengthofslope,thethicknessofplate

2.2 21.8°倾角、半径400 mm整体式U形砼衬砌的冻胀内力变化规律

依据规范(GB/T 50600—2010)，对于21.8°(边坡系数为0.4)倾角、半径400 mm的整体式砼衬砌渠道内力进行分析，依据规范，板厚可采用40～120 mm， 板长可采用400～900 mm。依据公式(8)～(13)可计算出不同板厚(4～12 cm)，不同板长(400 mm、500 mm)的衬砌冻胀内力，计算结果见表3和表4。

表3 板长400 mm的渠道衬砌冻胀内力Tab.3 Calculation with respect to the channel lining internal force of the slope at the length of 400 mm

表4 板长500 mm的渠道衬砌冻胀内力Tab.4 Calculation with respect to the channel lining internal force of the slope at the length of 500 mm

由表3、表4和图8～图11可知，21.8°倾角、半径400 mm整体式U形砼衬砌渠道与0°倾角、半径300 mm整体式U形砼衬砌渠道相比较，其法向冻胀力、最大拉应力和冻结力的变化趋势相似；板长400 mm衬砌的最大拉应力发生在离坡底49 %板长处，板长500 mm衬砌的最大拉应力发生在离坡底53 %板长度处，并随着厚度的增加，其位置有靠近坡底的趋势。

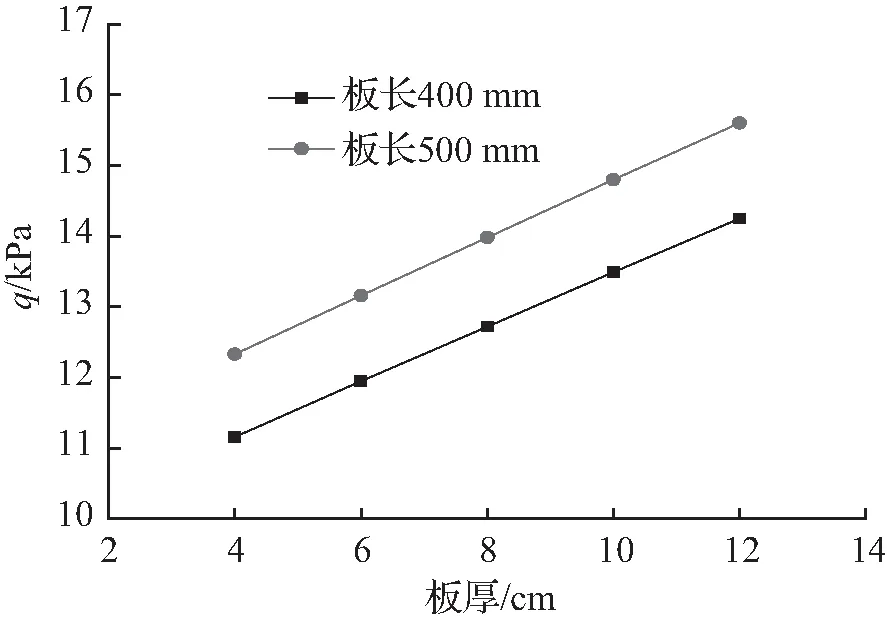
图8法向冻胀力与板长、板厚的关系
Fig.8Relationshipbetweenthenormalfrost-heaveforcesandradius,thethicknessofplate

图9最大拉应力与板长、板厚的关系
Fig.9Relationshipbetweenthemaximumstressoflininginnersurfaceandradius,thethicknessofplate

图10 切向冻结力与板长、板厚的关系Fig.10 Relationship between the tangential freezing force and radius, the thickness of plate

图11 最大应力位置与板长、板厚的关系Fig.11 Relationship between the maximum stress and radius, the thickness of plate

3 整体U形渠道衬砌冻胀内力的敏感性分析

整体式U形渠衬砌内力是在渠道衬砌半径、板厚、板长和倾角等4因素影响下的综合表现，这些因素都不同程度地影响U形渠衬砌冻胀内力的大小。由于影响因素较多，为了找到起控制作用的主要因素并加以分析和控制，进行了以上4因素3水平的正交试验，试验因素及水平取值见表5。

表5 因素及其水平取值Tab.5 Factors and its level

利用公式(8)～(13)计算渠道衬砌内力和极差分析，计算结果见表6。

由方差分析表6可知，4个因素对最大应力的影响大小依次为：板长>板厚>半径>倾角；对法向冻胀力的影响大小依次为：板长>倾角>板厚>半径；对法向冻结力的影响大小依次为：板长>倾角>板厚>半径；对最大拉应力发生位置的影响大小依次为：板长>板厚>倾角>半径。可见，板长为第一控制因素，其他因素次之，对不同分析对象各因素的影响不一致。由以上分析得出：从削减渠道衬砌最大拉应力方面而言，主要影响因素为板厚和板长，故在满足渠道断面流量的前提条件下，并考虑经济条件，尽可能采用“短坡厚板”设计，依据坡板衬砌冻胀最大拉应力很小的规则，利用相应公式可计算确定最佳厚度，以期减小渠道衬砌的冻胀破坏。

表6 正交表极差分析Tab.6 Analysis of range in the orthogonal table

4 弧形底梯形渠道冻胀内力的敏感性分析

弧形底渠道衬砌与整体式U形渠衬砌冻胀内力计算简图相似，其受力也与整体式U形渠衬砌受力相似，为了分析弧形底梯形渠道衬砌受力规律，考虑同样的影响因素，各因素的取值参考规范(GB/T 50600—2010)和文献[2]，按照4因素3水平安排正交试验，见表7。

表7 因素及其水平取值Tab.7 Factors and its level

利用公式(8)～(13)计算渠道衬砌内力，计算结果见表8。

表8 正交表极差分析Tab.8 Analysis of range in the orthogonal table

由方差分析表8可知，4个因素对最大应力的影响大小依次为：倾角>板长>半径>板厚；对法向冻胀力的影响大小依次为：半径>倾角>板厚>板长；对法向冻结力的影响大小依次为：倾角>板长>半径>板厚；对最大拉应力发生位置的影响大小依次为：倾角>板长>板厚>半径。可见，倾角为第一控制因素，其它因素次之，对不同分析对象各因素的影响不一致。对于不同几何尺寸混凝土衬砌，最大应力发生的位置也不同。理论上最大拉应力位置即为渠道实际渠道衬砌可能发生冻胀破坏的位置，实际渠道冻胀破坏位置也可能离最大拉应力位置较远，因为渠道衬砌破坏还受渠道材料缺陷和渠道衬砌板后的填土土质、含水量、压实系数等因素差异的影响。由以上分析可以得出：从削减渠道衬砌最大拉应力而言，主要影响因素为倾角和板长，在满足渠道断面流量和经济的前提条件下，尽可能采用“缓坡短板”设计，以期减小渠道的冻胀破坏，但边坡过缓，同样渠深，板长必然增大，故两因素要综合考虑进行渠道衬砌优化设计。

5 工程实例分析

作者对宁夏银川市西夏区军马场农场二队整体式U形渠道衬冻胀砌破坏进行了调研，并利用文中建立的力学模型对调研项工程实例进行了衬砌冻胀破坏情况分析。

对宁夏军马场农场二队约600 m长的U形渠道衬砌进行了现场调研，发现坡板衬砌冻胀破坏12块，调研现场见图12。混凝土渠道衬砌砼标号为C15，容重取γ=24 kN/m3，板长为 55 cm，弧底半径为 40 cm，衬砌板厚为 6 cm，坡角为 22°，τ=13.25 kPa，利用文中建立的模型计算出坡板最大应力位置(即易发生衬砌冻胀破坏处)和调研所获得的渠道坡板衬砌冻胀破坏位置见表9。渠道板冻胀破坏产生的断板裂缝以斜裂缝居多，见图12，裂缝位置量取了两处尺寸，取其平均值作为渠道衬砌板冻胀破坏位置，见表9。

图12 渠道衬砌冻胀破坏调研Fig.12 Channel lining of frost heaving damage research

破坏坡板序号破坏距离坡顶长度1/cm破坏距离坡顶长度2/cm距离坡顶平均长度/cm坡板长度/cm实际破坏位置/ %理论破坏位置/%1442936.55566.455.12474345.05581.83372129.05552.74321322.55540.95293029.55553.66351123.05541.87513342.05576.48453540.05572.79332026.55548.210293029.55553.611321423.05541.812392532.05558.2平均破坏位置/%57.3

由表9可知，坡板衬砌平均冻胀破坏位置为57.3 %，理论计算坡板衬砌平均破坏位置为55.1 %，为了确定理论破坏位置是否可以代表实际渠道破坏位置？对调研数据需要进行α=0.05的t检验：H0:μ=0.551，H1：μ≠0.551，检验统计量为公式(14):

(14)

代入调研数据，得到：

检验的临界值t0.025(11)=2.2010，即有|t|=0.56702.2010，样本值没有落入拒绝域，故接受原假设H0，认为渠道衬砌板的破坏位置为55.1 %，实例工程调研分析结果说明该模型确定渠道坡板衬砌冻胀的破坏位置科学合理。

6 结论

① 整体U形渠道衬砌和弧形底梯形渠道衬砌的力学计算简图相似，本研究考虑板厚、板长、倾角和半径对渠道衬砌的法向冻胀力、法向冻结力和切向冻结力的影响素建立了整体U形和弧形底梯形砼渠道衬砌冻胀内力的统一计算模型。

② 利用文中公式，假定渠道衬砌板最大拉应力接近1/10衬砌材料的允许拉应力为设计规则，依此规则可确定出渠道衬砌板的最佳厚度。

③ 从削减整体式U形渠道衬砌最大拉应力考虑，在满足渠道断面流量和经济的前提条件下，尽可能采用“短坡厚板”设计。

④ 从削减弧形底梯形渠道衬砌最大拉应力考虑，在满足渠道断面流量和经济的前提条件下，尽可能采用“缓坡短板”设计。

⑤ 渠道衬砌坡板最大拉应力产生的位置因为受到不同因素的影响，文中计算了多种尺寸组合模型，渠道衬砌尺寸不同，坡板最大拉应力产生的位置不同，利用文中建立计算模型对调研工程实例计算分析，说明该计算模型对计算渠道衬砌冻胀破坏具有借鉴意义。

文中建立的对称冻胀模型是在基本假设为线弹性、冻胀力假设为线性变化、假设法向冻结力在坡板处以及该处变形为零等较理想的条件下得到的，与实际有一定偏差，后期拟进行法向冻结力不同作用位置及坡顶不同变形量的非对称冻胀模型的研究。