大直径扩底人工挖孔桩承载力预测与数值验证

，，，，

(1.广西大学土木建筑工程学院， 广西南宁530004；2.广西防灾减灾与工程安全重点实验室， 广西南宁530004；3.桂林理工大学广西岩土力学与工程重点实验室， 广西桂林541004；4.中铁建设集团有限公司， 北京100040)

0 引言

随着超高层建筑的大规模建设，对其基础的承载力和变形要求不断提高。大直径扩底人工挖孔桩因其承载力大、沉降小、抗震性能好、施工质量容易控制等优点通常用作超高层建筑的地基基础[1-3]。为避免大直径扩底桩承载力偏小导致地基失稳及过大而浪费材料，工程界亟需一种能准确计算大直径扩底人工挖孔桩极限承载力的方法。

由于大直径扩底人工挖孔桩承载力较高，试验中无法提供如此大的反力系统而不能用常规的静载荷试验来得到其极限承载力。目前常用的方法有理论计算、经验估算、有限单元法等[4-5]。理论计算方法由于计算结果可靠、适用性强等优点，国内外研究人员对其进行了许多有益研究，并相应提出了扩底桩承载力计算理论。Mayerhof[6]通过对不同砂土的扩底桩承载特性进行分析，提出扩底桩的承载力应按不同土体密实度取用不同折减系数。黄强[7]把桩端变形近似划分为两个阶段，并通过扩底桩的变形特征给出相应计算公式。邓洪亮[8]基于固体力学和弹性理论对桩—土作用的荷载传递机理进行分析，提出了考虑深度效应的扩底桩承载力的理论解。

可以看出，目前国内外研究人员关于桩端位移计算主要采用线弹性理论。而大直径扩底桩的承载力由端阻控制，其端阻力可达总承载力的80 %以上，在巨大的桩端荷载作用下岩基变形模量呈非线性变化[9]。因此，采用非线性模量计算桩端位移更加符合工程实际情况。本文基于岩基载荷试验结果，提出了一种更能反映实际桩土体系受力性状的大直径扩底人工挖孔桩极限承载力预测模型，并结合数值模拟对该方法进行验证。基于此预测模型对大直径扩底桩相关参数展开分析，探究桩身几何参数对大直径扩底人工挖孔桩承载力的影响规律。

1 工程背景

1.1 工程概况

广西九洲国际工程项目，场地位于南宁市埌东开发区，其总建筑面积214 729.8 m2，总建筑高度317.6 m，地上71层，地下6层，地下室埋深26.5 m，地基基础设计等级为甲级，场地地貌属于构造剥蚀丘陵地貌。主楼采用大直径扩底人工挖孔桩基础，桩基持力层为中风化砂岩，桩基设计等级为甲级，共设计36根扩底桩，最大桩身直径为4.0 m，扩底直径为5.6 m。根据该场地土工试验和原位测试成果，结合该场地岩土工程勘察报告，该工程场地各地层的主要物理力学性质见表1。

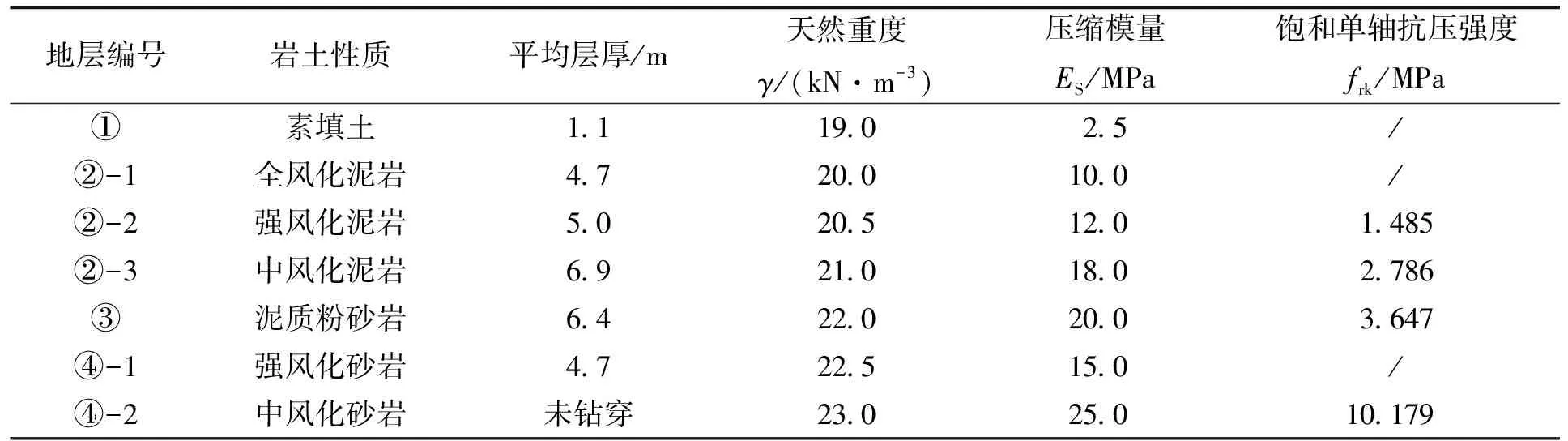
表1 各岩土层物理性质指标Tab.1 Geotechnical physical and mechanical parameters of soil

1.2 岩基载荷试验

由于该工程单桩承载力设计值最大达128 000 kN，成桩后极限承载力测定时无法提供如此大的反力系统，不能进行常规静载试验。又因为按室内岩石饱和单轴抗压强度乘以折减系数得到的岩石地基承载力远低于岩石地基的实际承载力[10]，而岩基原位载荷试验确定性高、安全可靠，对积累地区经验具有重要的意义和实用价值[11]。因此对工程10#桩孔进行岩基载荷测试确定桩端岩土性质，试验结果见图1。

地基变形模量按弹性理论采用Boussinesq解，地基土处于半无限弹性体内，计算公式为：

(1)

式中：p为压力(kPa)；b为平板直径(m)；ω为沉降影响系数，取0.785，v为泊松比；s为沉降值(mm)。

根据岩基载荷试验数据，由式(1)得到变形模量，采用指数函数模型，将各级压力下的变形模量进行拟合，指数函数模型公式为：

(2)

式中，A1，t1，y0是需要确定的3个参数，它们与试验岩基的性质息息相关。同一地基不同测试点，得到的3个参数也有所差异，但在同一地基上，可以根据大量实测数据得出其各自的取值范围。

图2为桩端持力层的变形模量随压力变化曲线，由图可知随着压力增大，持力层变形模量逐渐减小，最后趋于稳定。通过拟合得到近似的函数关系式(3)，可以预估出任一压力下该测点处的岩基变形模量。该关系式可用于下文桩基极限承载力预测模型，即用荷载传递法计算桩端位移时，桩端传递函数可以考虑非线性模量的情况:

(3)

图1岩基载荷试验荷载—沉降曲线
Fig.1Load-Settlementcurveofplate-bearingloadtest

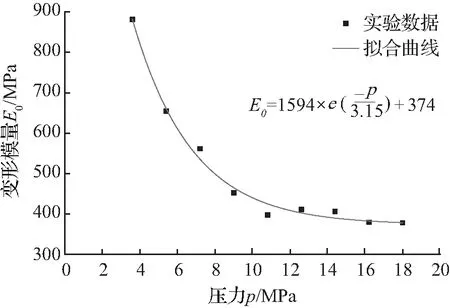
图2变形模量拟合曲线
Fig.2Deformationmodulusfittingcurve

2 承载力预测

2.1 计算模型

本文大直径扩底桩承载力预测模型基于荷载传递法，式(4)为桩—土体系荷载传递的基本微分方程，其中，u为桩身周长，Ep为桩身弹性模量，Ap为桩身截面积，

(4)

为求解此微分方程，桩侧采用由Gardner(1975)提出的桩侧双曲线传递函数[12]，如下式所示：

(5)

其中，A为试验常数，S(z)为桩土相对位移，Ks为初始切线模量。τu的计算一般采用α法和β法，但对于本工程中桩土层为强风化砂岩的情况，这两种方法并不适用。《建筑桩基技术规范》给出了不同土层桩的极限侧阻力qsik的经验参数，更加接近实际情况，故采用其给出的qsik作为桩侧极限摩阻力τu。

而对于桩端传递函数，基于刚性圆面积上的Boussinesg解，根据Fleming (1992)和Delpak (2000)的研究建议[13]，可采用下式计算：

(6)

其中，vb为桩端下土体平均泊松比，D为桩径，E为桩端下土体的平均模量，η为考虑深度效应的折减系数。

在实际工程中，由于桩端土的平均模量E随压力的变化而非线性变化，E可采用基于现场岩基载荷试验实测数据计算得到的变形模量，更能真实反映实际情况。通过图2曲线，即可得到任一压力下的桩端平均模量E。

2.2 计算方法

已知荷载传递函数，则解式(4)微分方程即可得到单桩的荷载传递情况，目前求解该方程的方法有解析法、位移协调法以及矩阵位移法。本文利用位移协调法，桩侧采用双曲线荷载传递函数，桩端采用考虑变模量的非线性传递函数，由假设的桩端位移计算桩顶荷载—沉降关系，计算步骤为：

① 已知该大直径扩底桩的特征值、桩侧传递函数曲线τ(z)-S(z)以及桩侧和桩端土物理性质指标。

② 将桩身根据地基分层情况，或同层内等分，分成n个单元，每个单元视为一个摩擦段，则单元长h=(L-hc)/n。

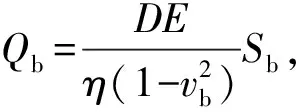
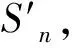
⑤ 求得第n段桩单元顶面处的轴力Qn-1=Qn+τnuh。

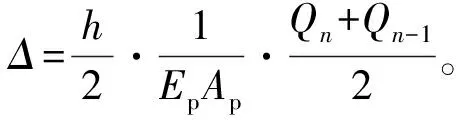
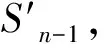
⑨ 逐渐向上一个单元递推，直到桩顶的首个单元，即可求得对应于此次假定的桩端位移Sb的桩顶荷载Q0及桩顶沉降量S0。

⑩ 重新设定下一级的桩端位移，然后回到上述(3)～(9)步，便可以得到桩顶荷载—位移曲线(Q0-S0曲线)。

通过MATLAB编写预测模型程序，输入桩和土的材料参数，假定不同的桩端位移即可得到不同的桩顶荷载和桩顶位移，作图可得桩顶Q-s曲线，运用变形控制的原则，在图上划出40 mm桩顶沉降对应的桩顶荷载值，该值即为单桩极限承载力预测值。

2.3 计算结果

图3 扩底桩Q-s曲线Fig.3 Load-Settlement curve of the belled pile

预测模型采用桩长9.2 m，直径4 m，扩底段标高2.8 m，扩底直径5.6 m的扩底桩，用C40钢筋砼，弹性模量为32.5 GPa，地基岩土参数根据工程实际数据取值。通过本文预测模型简化计算绘制的Q-s曲线如图3所示。

从图3可以看出，大直径扩底桩的Q-s曲线呈缓变型，在加载前期的低荷载水平下，曲线大体呈线性增长，每级加载下桩顶沉降增量不大，但当荷载逐渐增至极限荷载后，桩顶沉降量有明显增大趋势。由图可看出该曲线较平滑，没有明显的特征点来确定极限承载力，宜用桩顶位移控制原则确定其极限承载力，可得本模型中该大直径扩底桩极限承载力为176.6 MN。

3 数值验证

3.1 有限元模型

为验证预测模型的合理性，拟借助ABAQUS建立三维弹塑性数值模型对桩基静载荷试验进行数值分析。参照有关学者[14]的计算经验并经试算，确定地基模型尺寸为40 m×40 m×40 m，考虑到实际工程中的土层分布情况，桩侧为泥质粉砂岩③层，桩端持力岩层为中风化砂岩④-2层，持力层下还有泥质粉砂岩③层夹层，最底部是较厚的中风化砂岩④-2层，如图4所示，本构模型均采用Mohr-Coulomb模型，具体参数如表2所示。

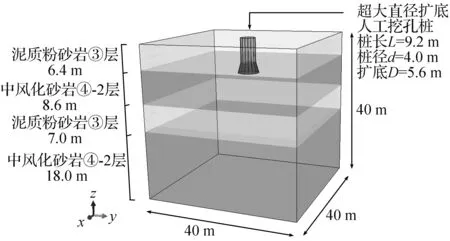
图4 桩基静载荷试验模型Fig.4 Static load test numerical model

岩土层层厚/m弹性模量/MPa泊松比密度/(kg·m-3)内摩察角/(°)黏聚力/kPa泥质粉砂岩③0～-8-15～-221 2800.152 20020450中风化砂岩④-2-8～-15-22～-401 6000.202 30020500

桩基模型参照广西九洲国际工程实际建立，参数选取依据工程实际情况，与预测模型参数一致。标准工况采用桩长9.2 m，直径4 m，扩底直径5.6 m的超大直径扩底人工挖孔桩，桩身砼为C40，具体参数见表3。

表3 扩底桩模型参数Tab.3 Parameter of the belled pile

模型中设置扩底桩与桩侧、桩底岩土体接触，其接触面采用表面—表面接触，滑移公式采用小滑移，切向摩擦公式采用罚函数，摩擦系数为0.3，法向采用硬接触，允许接触后分离。网格划分如图5和图6所示。

土体共划分为20 864个单元，扩底桩划分为2 700个单元，两者均采用C3D8单元进行结构划分，桩端与桩底接触部分岩土体网格加密，网格划分如图5和图6所示。

桩基静载试验的加载分为十级荷载，每级在桩顶叠加1.8 MPa的压力，相当于22.62 MN的桩顶压力，直至加载到第十级荷载226.20 MN。

图5岩土体网格划分
Fig.5Meshgenerationofthefoundationsoil

图6扩底桩网格划分
Fig.6Meshgenerationofthebelledpile

图7 扩底桩数值模拟结果与预测模型对比Fig.7 Comparison of numerical simulation with prediction models of the belled pile

3.2 计算结果

将有限元计算得到的桩顶荷载—沉降曲线和上文预测模型计算得到的曲线置于同一图中对比如图7所示。

从图7可以看出，两条曲线吻合较好，相互印证了两种方法的可靠性。加载前期，预测模型的Q-s曲线和有限元计算结果基本重合，可以看出在低荷载水平下，两条曲线都基本呈线性增长。在中等荷载水平下，有限单元法计算的桩顶位移比预测模型稍小，究其原因，发现有限元计算的桩侧摩阻力发挥情况和预测模型得到的结果有所差别，并不是预测模型中标准的双曲线函数模型，而实际工程中摩阻力的发挥情况十分复杂，理论方法并不能很精准的模拟实际情况。

在位移控制点40 mm处，由数值模型计算得到扩底桩的Qu1=182.0 MN，预测模型计算得到扩底桩的Qu2=176.6 MN，两条曲线的极限荷载相差不大，说明本文的预测模型能够较好地预测大直径扩底人工挖孔桩的极限承载力，指导大直径扩底人工挖孔桩的设计计算。

4 参数分析

为了得到桩身几何参数对大直径扩底桩承载力的影响规律，指导大直径扩底人工挖孔桩的设计计算，基于本文得到的单桩承载力预测模型，对这些影响因素如桩长、桩径、扩底直径进行详细的分析。预测模型的基本几何参数见表4。

表4 预测模型的基本几何参数Tab.4 Basic geometric parameters of prediction model

4.1 桩长的影响

图8表示桩长分别为9.2 m、13.2 m、17.2 m和21.2 m，其他因素不变时，大直径扩底桩的桩顶荷载—沉降曲线。由图8可知，不同桩长的单桩Q-s曲线变化不明显，随着桩长的增加，极限荷载略微增大，对应的极限荷载均为170～190 MN左右。由此可见，虽然随着桩长的增加，桩侧摩阻力分担的荷载相应增加，但是大直径扩底桩的承载力主要由端承力提供，不能通过增大桩长来有效提高承载力，经济性不佳，对于此类嵌岩桩只需将桩底牢固地嵌入岩基中即可。

4.2 桩径的影响

图9表示桩径分别为4.8 m、4.0 m、3.2 m和2.4 m，其他因素不变时，大直径扩底桩的桩顶荷载—沉降曲线。由图9可知，随着桩径的增大，同一荷载作用下的单桩沉降显著减小，承载力增大，不同桩径单桩对应的极限荷载范围为110 MN～240 MN，各桩径承载能力差异明显。因此，对于大直径扩底人工挖孔桩来说，桩端承载力为其主要承载力，增大桩径能显著提高桩的极限承载力，但是在实际工程中，同样需要考虑到经济性和适用性条件。

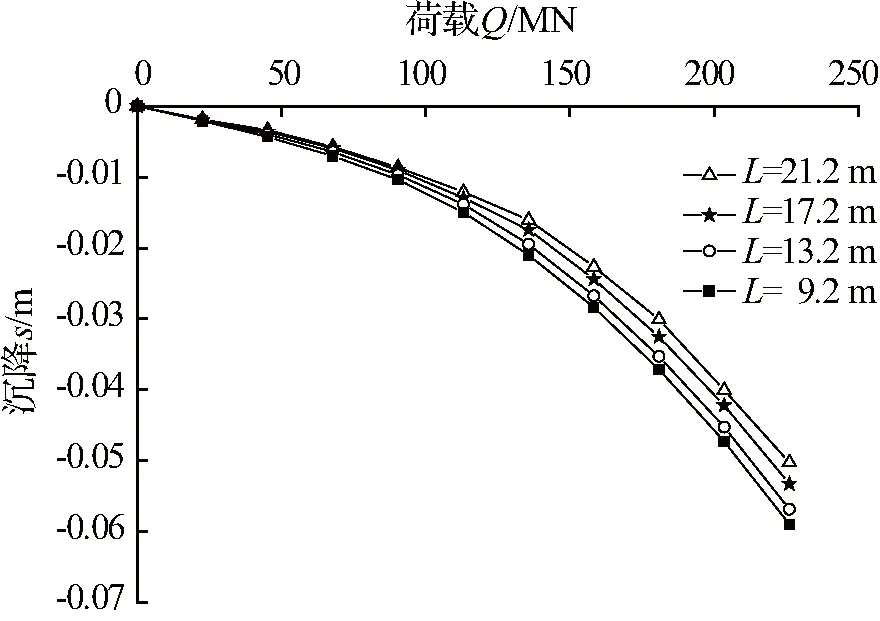
图8不同桩长时的Q-s曲线
Fig.8Load-Settlementcurveunderdifferentlengthofthepile

图9不同桩径时的Q-s曲线
Fig.9Load-Settlementcurveunderdifferentdiameterofthepile

图10 不同扩底直径的Q-s曲线Fig.10 Load-Settlement curve under different bellout diameter of the pile

4.3 扩底桩径的影响

图10表示扩底直径分别为4.0 m(等直桩)、4.8 m、5.6 m(标准)、6.4 m、7.2 m，其他因素不变的情况下，大直径扩底桩的桩顶荷载—沉降曲线。由图10可知，扩底桩径的大小对扩底桩承载变形特征有显著影响。随着桩径的增大，大直径扩底桩的Q-s曲线更趋平缓，同一荷载作用下的桩顶沉降显著减小，扩底直径为5.6m的扩底桩相比同桩径等直桩承载力提高53 %，增加较小扩底桩径就能得到较大的承载力提升，且相比增加桩径提高承载力能有效减少混凝土用量，经济效益明显。因此在工程地质条件容许的情况下应当尽可能使用扩底桩以提高人工挖孔桩的极限承载力。

5 结论

针对大直径扩底桩极限承载力难以确定问题，本文通过岩基载荷试验得到不同荷载作用下的岩基变形模量，基于荷载传递法，提出了一种更能反映桩土体系受力性状的大直径扩底人工挖孔桩极限承载力预测模型，并用数值模拟验证其可靠性。在此基础上，对大直径扩底桩承载力进行参数分析，得到以下主要结论：

① 岩基变形模量随着荷载水平的增加而减小，岩体变形增大，后趋于稳定，岩基无明显的弹性变形阶段。岩基的变形模量随压力的变化曲线可用负指数函数拟合，通过拟合得到近似的函数关系式，可以预估出任一压力下，该测点处的岩基变形模量。该关系式可用于桩基极限承载力预测模型，即在用荷载传递法计算桩端位移时，桩端传递函数可以考虑非线性模量的情况，更能反映实际桩土体系受力性状。

② 本文提出的预测模型计算得到的Q-s曲线和有限元软件模拟得到的结果吻合较好，曲线皆呈缓变型，两者极限承载力计算结果接近，验证了该预测模型的可靠性。该预测方法可供今后类似工程借鉴，指导大直径扩底人工挖孔桩的设计计算。

③ 通过本文得到的预测模型可知，南宁软岩互层地基桩基表现出摩擦端承桩的特性。桩长对桩的极限承载力影响相对较小，桩长21.2 m扩底桩相比同参数情况下9.2 m桩长扩底桩承载力仅提高11.7 %；而桩径对桩的极限承载力影响较大，桩径4.8 m扩底桩相比同参数情况下2.4 m桩径扩底桩承载力提高118 %。在实际工程应用时，考虑到经济性等因素，相较于增加桩长，增大桩径对于提高单桩承载力效果更好。

④ 相比于同参数下的等直径桩，扩底直径为5.6 m的扩底桩承载力提高53 %，增加较小扩底直径就能明显提高承载能力，且有效减少混凝土用量，经济效益明显。因此在工程地质条件容许的情况下应当尽可能使用扩底桩以提高人工挖孔桩的极限承载力。