基于向量机方法的基坑工程预警系统研究

，*，，，，

(1.大连海事大学交通运输工程学院道桥所, 辽宁大连116026;2.中交隧道工程局有限公司， 北京100102)

0 引言

预应力锚索支护技术通过施加高预紧力对锚索支护范围内的围岩产生有效的径向约束，锚索与围岩共同组成自承载结构，充分提高岩土体自身强度的同时显著减小结构自重，有效的维持了结构的稳定性[1]。根据不同的岩体强度理论，众多学者对锚索的作用机理进行了多种探索及解释[2-4]，但是由于预应力锚索与围岩作用机理的复杂性及周围地层结构的不确定性，至今尚无可应用于所有工程的普适方法。

支持向量机作为一种能够进行自学习的算法，可以很好地解决岩土工程中多参数、大变量、地层条件复杂且难以预测等问题。赵洪波，冯夏庭等[5-7]对向量机在岩土工程中的应用做了较为详细的研究，结果表明支持向量机方法可对边坡施工过程中的滑动面确定、稳定性预测分析等目标函数实现有效的计算。姜谙男[8]通过粒子群算法与支持向量机的结合，对洞室围岩变形时间序列进行了预测研究，证明了模型在隧道工程中的可靠性。基于时间序列的向量机计算具有较好的稳定性和普适性，但是单纯的基于时间序列的计算方式可能会出现误差累积等问题，应考虑进一步完善支持向量机的预测过程以避免这些问题的产生。

为了实现对基坑工程的实时监测，同时对可能出现的工程灾害进行超前预警，研制开发了岩土工程自动化监测预警系统并应用于青岛城市轨道工程建设中。该系统依托多元信息集成方法实现数据的实时监测，通过最小二乘支持向量机方法对锚索拉力进行计算，基于改进的时间序列滚动预测法对未来的锚索拉力值进行预测，在滚动过程中同时考虑气温、地下水位等因素的影响，以此对可能产生的计算误差进行及时修正。

1 多元信息监测系统

借助振弦式钢筋计、应力计等自动化传感采集硬件实现多目标参数的实时监测与数据采集，将传感器网络分布式嵌入至工程需监测位置，并在此基础上采用无线通讯技术进行数据传输。具体量测项目参考基坑工程监测技术规范[9]，基于YT-ZD-01型自动采集箱对终端采集到的数据信息进行汇总处理，处理后数据经由GPRS模块上传至云服务系统，实现数据的远程获取。多元信息采集系统如下图所示。

图1数据采集模型
Fig.1Dataacquisitionmodel

图2自动化采集箱
Fig.2Automatedcollectionbox

图3 计算判定流程图Fig.3 Calculation and judgment flow chart

数据采集系统实现了监控测量的遥控化，在避免了人力物力浪费的同时，可实现多项内容的同时测量，并且这种测量结果可在任意时刻获得。与此同时，自动化的采集过程避免了人工测量可能会产生的误差，测量结果更精准，监测所得数据通过计算机系统进行处理，基于LSSVM方法进行计算分析，解决了人工处理冗杂繁多数据过程中效率低下的问题。

LSSVM计算判定过程如图3所示，在当前日对此后3 d的数据进行滚动预测，即每组数据在实测前会进行3次预测计算。若预测值超出警戒值，但是所预测的日期与当前日相差大于一天，则考虑计算可能存在的误差及岩土体的自我调节能力，暂不做预警处理，而是加强数据的自动化采集密度，对危险结构面进行实时监测；若某一位置的预测值连续3次超出警戒值，则系统发出超前预警。

2 基于最小二乘法的支持向量机

基于统计学习理论的VC维理论和结构风险最小化的支持向量机[10]可实现在小样本、非线性的条件下进行学习预测计算的功能。SVM方法通过二次型寻优得到全局最优解，在求解过程中仅需确定不敏感系数ε、惩罚因子C、核函数宽度系数σ等3个参数，较好地解决了神经网络训练容易陷入局部最优化、BP网络建模复杂等问题。但是传统SVM方法训练样本时需求解二次规划问题，计算速度较慢。最小二乘法支持向量机(least squares support vector machine, LSSVM[11])采用最小二乘价值函数和等式约束, 将传统的二次规划问题求解转变为线性问题, 很大程度上提高了计算速度。

LSSVM 的回归预测可认为是用一个超平面对已知数据进行拟合的过程。对于给定的N个训练样本{xi,yi}i=1…N(其中xi∈Rn为n维训练输入样本，yi∈Rn为训练输出样本)，目标优化函数为

(1)

式中：φ(·):Rn→Rnf为核空间映射函数；ω∈Rnf为权矢量；ek∈R为误差变量；b为偏置量；γ为可调参量；yk不再是类别标签，而是估计函数y=f(x)中的y。

LSSVM回归函数：

(2)

训练误差最小化和平滑程度之间的权衡程度通过正则参数γ来体现；高斯RBF核中的平方带宽通常情况下以σ2表示，这两个参数的取值结果决定了所采用径向基核函数的性质，文中在应用最小二乘支持向量机进行计算过程中，通过预留一个依赖于样本大小的交叉验证来自动调整这两个参数。相对于传统支持向量机，LSSVM算法复杂性的优势体现在其复杂性的弱化，这种弱化得益于所需求解的优化问题通过最小二乘价值函数和等式约束转化成为线性方程。

3 锚索拉力变化的向量机模型

3.1 锚索拉力变化的向量机表示

对锚索拉力进行监测，通过现场测量已获得的数据记为一个锚索拉力随时间变化的时间序列{xi}={x1,x2,…,xN},对这个非线性变化序列进行预测，就是要寻找在p+1时刻的锚索拉力值与前p个时刻的锚索拉力值x1,x2,…,xp的关系，即xp+1=f(x1,x2,…,xp)为学习函数，表示锚索拉力变化序列之间的非线性关系。

根据最小二乘支持向量机理论，上述非线性变形关系可以通过支持向量机对p个已获得的实测锚索拉力值学习来获得，也就是通过对n-p个变形序列xi,xi+1,…,xi+p,(i=1,2,…,n-p)的学习，来获得锚索拉力变化序列之间的非线性关系，即：

(3)

式中：y(xp+1)为第p+1时刻的锚索拉力值；xp+1为p+1时刻处前p个锚索拉力值，xp+1=(x1,x2,…,xp+1)；xk为p+k时刻位置处的前p个锚索拉力值，xk=(xk,xk+1,…,xk+p+1)。

3.2 修正的动态滚动预测方法

假设通过现场测量已获得的锚索拉力变化序列为{xn}，需要以此作为学习样本并进一步预测之后的数个时间序列xn+1,xn+2…，最佳历史步数设为P。在上述的条件下，学习样本的映射形式设置为{x1,x2…xp}→{xp+1},{x2,x3…xp+1}→{xp+2}…{xn-p,xn-p+1…xn-1}→{xn}。向量机学习的结果是可通过预测点前p个历史数据预测当前位置的数据，例如需要预测xn+1，只需输入，{xn-p+1,xn-p+2…xn}即可得到预测结果；继而将预测获得的xn+1作为已知量，将{xn-p+2,xn-p+3…xn+1}作为一个新的时序对xn+2进行预测，依此类推。滚动预测方法未通过影响锚索拉力的气温、地下水位、支撑长度、架设时间等影响因素直接作为学习过程的映射输入值，而是将已测得的锚索拉力数据自身作为预测依据，保证了预测结果不会由于未考虑足够因素而出现偏移。

上述方法在很大程度上解决了施工过程中影响因素多、部分参数无法精准确定等问题，但是预测过程中每一个预测步仍不可避免的存在某些误差，随着预测步数的增加，这种误差不断累积，最终可能导致预测结果无法准确表达真实工况。为了减小这种误差的影响，在输入时序中加入Q个可以准确确定的影响参数，对每一步预测过程进行有效地修正。本文影响因素的数量设置为2，假设An,Bn分别代表影响锚索拉力的两种不同的外界因素在第n天的测量值，上述的学习样本的映射方式变化为{Ap+1,Bp+1,x1,x2…xp}→{xp+1}。对xn+1的预测计算输入时序变化为{An+1,Bn+1,xn-p+1,xn-p+2…xn}。

锚索拉力变化的最佳历史步数p和影响因素Q的确定对预测结果有很大影响，可以通过优化算法来进一步完善，本文通过对比方法确定其取值。

3.3 预测参数的选取

经对比验算，向前滚动预测3步内预测结果精确度较高，第4步开始出现预测误差。据此，本工程预测步数设置为3，即对实测值位置后的3组锚索拉力值进行预测。由于影响因素取值无法提早预知，预测过程中第一组采用改进预测法，另两组在第一组的预测结果基础上采用基本滚动预测法。

地下水位对基坑稳定性的影响主要是由于承压水层改变所导致的[12-14]，水位过高会导致坑底隆起，两侧围护墙体产生差异沉降导致支撑失稳断裂；水位长时间偏低，会使得围护墙在坑底部分受弯甚至发生不可逆变形，上部已安装支撑受力过大而发生挠曲，导致支撑失稳破坏[15]。由此可见，地下水位对基坑稳定性的影响是一个变形累积导致破坏的过程，即第n天的水位变化对基坑坑底、围护墙及锚索拉力产生的影响在n+1天甚至更久之后才能体现。在此，充分考虑地下水位作用效果的滞后性，将第n天测得的水位值作为第n+1天锚索拉力变化的预测影响参量。考虑目前的数值天气预报方法已较为完善[16]，第n天时刻下直接采用第n+1天的温度预报值作为锚索拉力变化的预测影响参量。

4 实例分析

青岛西海岸经济新区城际轨道交通项目是贯穿西海岸经济新区的轨道交通骨干线和快速线，将整个青岛市西海岸经济新区融入全市轨道交通网，形成青岛市“一谷两区”格局的互联互通。线路位于青岛市西海岸新区，总体呈东北—西南走向。工程划分为12个区段，共包含12个车站，本文以井冈山车站基坑工程为背景进行预测计算。车站中心里程为YCK7+680，结构形式采用三层双柱三跨结构，施工工法为明挖顺做法。结合青岛地质条件特点及该地区深基坑施工设计经验，确定车站主体围护结构在一期东西两施工段设置一道6根间距4.5 m的对拉锚索，其它部分采用钻孔桩+预应力锚索+岩石锚杆的形式，主体围护桩采用A1000(部分为A800)钻孔灌注桩，嵌固深度为中风化层2.5 m。

按照第3节所述的计算方法，分别用常规的滚动预测法与修正后的滚动预测法对锚索拉力数据进行学习计算。选择变形序列的历史最佳点数为3，同时将温度，地下水位作为决定锚索拉力值的影响因素。以表1中的44 d实测数据组成41组学习样本，建立基于最小二乘法的支持向量机模型。计算获得常规滚动算法对应的参数为：y=3.988 6,σ2=9.505 4，改进的滚动算法对应的参数为：y=9.505 0,σ2=56.961 3。两种模型的学习曲线见图4。

表1 青岛地铁井冈山站基坑工程ML2-2监测数据Tab.1 Detection Data of ML2-2 in Foundation Pit Engineering of Jinggangshan Station in Qingdao Subway

图4模型学习曲线
Fig.4Curveresultofmodellearning

对于不同学习方法，其学习曲线形状不完全相同(图中标出位置)，关键参数γ与σ2的计算结果也存在差异，但两种学习方式均较好地实现了对数据点的拟合，改进方法的学习曲线拟合度相对较高。基于已有的向量机学习结果，采用滚动预测的方式对未来3 d的深基坑锚索拉力变化进行预测，预测结果及误差分析见表2。

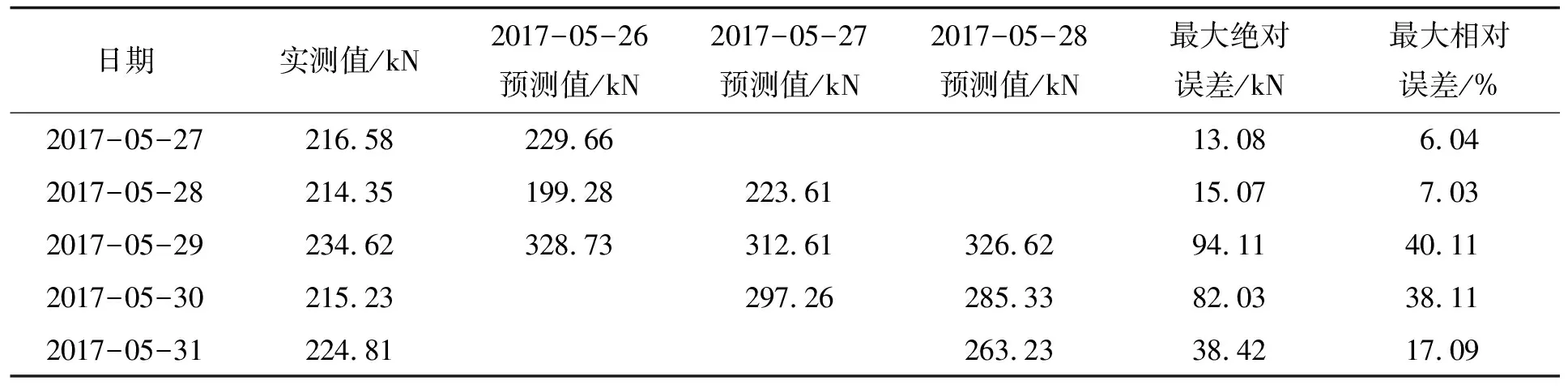
表2 支持向量机预测结果Tab. 2 Prediction results of support vector machine

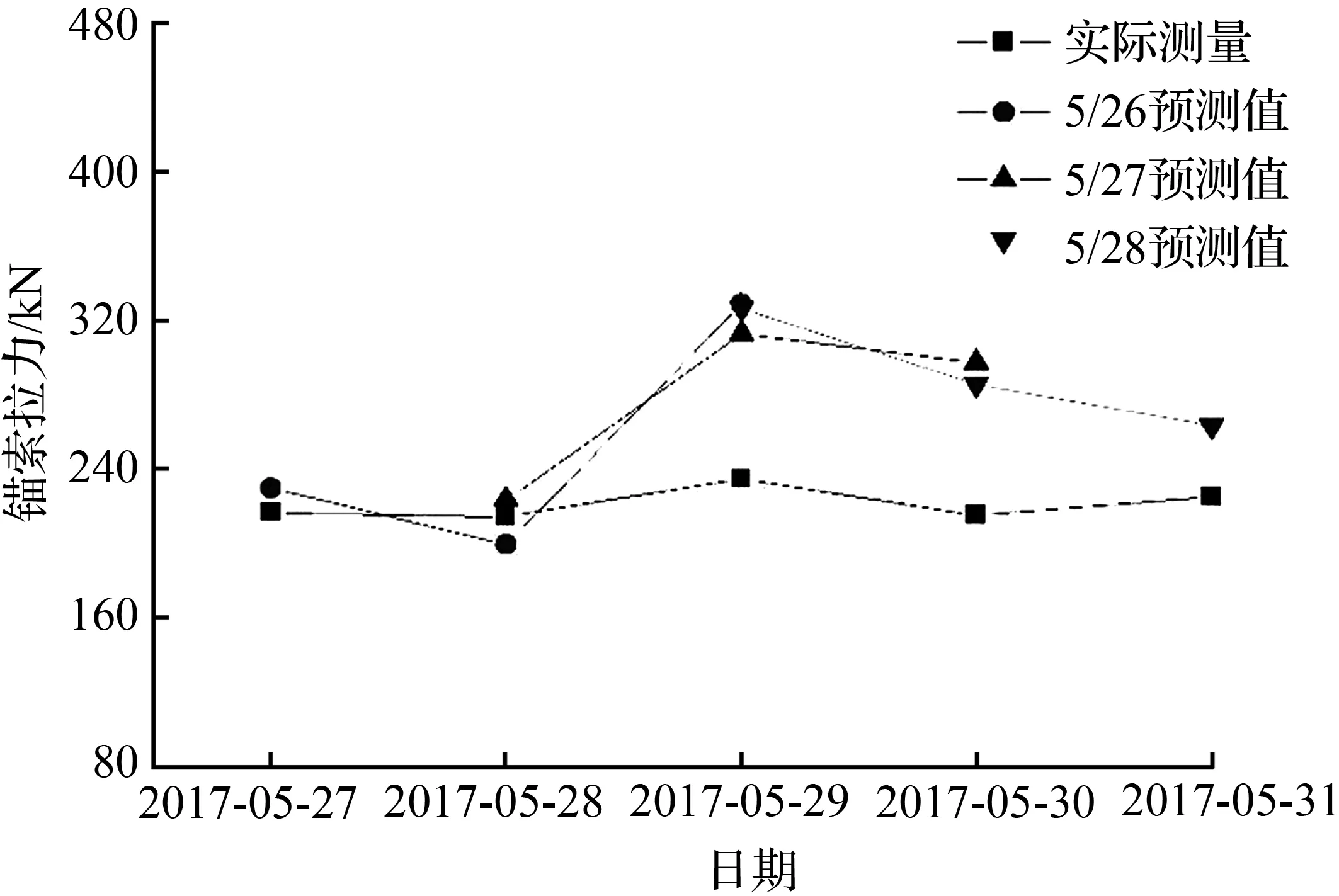
图5 变形预测值和监测值的比较Fig.5 Comparison of deformation predictions and monitoring values

由表2和图5可以看出，5月29日之前，预测数据与监测数据基本一致，最大绝对误差为15.07 kN，最大相对误差为7.03 %。5月29日锚索拉力预测值连续3次远大于设计最大值，系统发出超前预警。在此警报信息的基础上，会同设计单位和施工单位，结合实际地质条件与结构特点进行了现场勘查，并进一步共同商定了加固方案，于5月28日对报警位置对应结构面实施锚索加密与灌浆加固处理。加固后监测结果表明，29日锚索拉力实测值出现小幅度增长但仍处于设计值范围内，后续监测数据逐渐趋于平稳，说明基于预警信息的加固措施有效防止了施工灾害的发生。结果表明最小二乘法支持向量机可以很好地表达锚索拉力与其他影响因素之间的映射规律，能够较好地适应青岛基坑工程，同时表明本预警系统可有效地对基坑工程潜在危险实现超前预警。

5 结论

① 多元信息采集系统可对施工过程中的相关参数实现实时监测与采集，大幅节省了监测成本，同时避免了人工测量可能产生的误差，提高了监测结果的可靠性与准确性。

② 针对岩土工程所具有的复杂性、高度非线性等特点，综合应用基于时间序列的滚动预测和基于影响参数的映射预测是十分有效的，预测结果可较为准确地表达实际工程问题。

③ 将该预警系统成功地应用于青岛城市轨道交通工程的基坑施工过程中，实现了对施工过程的实时监测与超前预警，确保了施工安全有序进行。