考虑高阶振型影响的输电塔抗震性能评估方法

,,,4,*

(1.广西大学土木建筑工程学院， 广西南宁530004；2.工程防灾与结构安全教育部重点实验室， 广西南宁530004；3.广西防灾减灾与工程安全重点实验室，广西南宁530004；4.浙江省交通运输科学研究院， 浙江杭州311305)

0 引言

输电塔是重要的生命线工程，保障其安全性十分重要[1-2]。对于大量修建于高地震烈度区的输电塔，地震作用常使其发生不同程度的破坏，直接威胁电力正常供应与人们生命财产安全[3-6]，因此开展输电塔的抗震性能评估非常必要。

Pushover法是工程结构开展抗震性能评估的常用方法[7-9]，而传统Pushover法的侧向力分布模式主要采用倒三角、多振型、均布等固定分布模式，未考虑高阶振型对抗震性能的影响，所以难以准确分析输电塔等高耸结构的抗震性能[10-11]。对此，目前发展了多种考虑高阶振型的改进Pushover法，具有代表性的包括考虑高阶振型的模态Pushover法[12]以及考虑动力特性的自适应Pushover法[13]等。上述方法具有计算精度高的优点，但是计算过程较为复杂，与传统Pushover法简便易行的优点不协调[14-15]。对此，Kunnath[16]考虑各振型响应的正负差别，提出了考虑高阶振型的振型侧向力组合方法(Modal Lateral Force Combination, MLFC)，该方法克服了模态Pushover需要多次进行Pushover分析、自适应Pushover需要在每个荷载步检查与调整侧向力所存在的繁琐过程[17-18]。文献[19-20]基于传统侧向力分布模式对输电塔抗震性能进行研究，但未能考虑由于输电塔高耸且柔度大等特点所引起的高阶振型显著的影响。因此有必要提出一种能够有效考虑高阶振型影响的输电塔抗震性能评估方法。

鉴于此，本文首先基于MLFC确定了侧向力组合模式，并采用能力谱法分析了输电塔的能力曲线和性能指标；然后根据输电塔的抗震性能目标和顶部位移性能水准进行抗震性能评估，提出了能够有效考虑高阶振型影响的输电塔抗震性能评估方法，并以增量时程分析法为基准，与传统方法进行了对比验证分析。

1 考虑高阶振型影响的能力谱法

1.1 振型侧向力组合模式

根据振型侧向力组合方法(MLFC)[16]，侧向力计算公式为：

(1)

式中：Fi为第i质点作用的侧向力；N为振型数；Rj为第j阶振型的振型贡献系数；Γj为第j阶振型的振型参与系数；M为结构质量矩阵；φj为第j阶振型；Sa(ζj，Tj)为阻尼比ζj、周期Tj时第j阶振型谱加速度。

式(1)通过振型贡献系数Rj引入了振型间的相互耦合，保证各振型组合侧向力Fi能较准确地模拟地震动作用[21-23]。本文基于文献[22]的研究成果，将Rj定义为振型参与质量系数的相对比值：

(3)

式中：αmax为前j阶振型的振型参与质量系数的最大值；αj为第j阶振型对应的振型参与质量系数，计算公式为：

(3)

式中：I为单位矩阵；mi为第i质点的质量；K表示质点总数。当考虑各振型侧向力的正负向组合时，j阶振型由式(1)可组合出2j-1种侧向力组合模式。以2阶振型为例，可组合出侧向力组合模式为：

F1=R1Γ1Mφ1Sa(ζ1,T1)+R2Γ2Mφ2Sa(ζ2,T2)F2=R1Γ1Mφ1Sa(ζ1,T1)-R2Γ2Mφ2Sa(ζ2,T2),

(4)

其侧向力组合模式如图1所示。

图1 考虑2阶振型的侧向力组合模式Fig.1 Lateral force combination patterns considering two modes

1.2 能力谱的确定

通过基于侧向力组合模式的Pushover法，可以获得考虑高阶振型影响的底部剪力与顶点位移(Vb-ur)曲线。在将Vb-ur曲线转化为能力谱曲线时，可采用结构等效振型考虑高阶振型的影响[24]：

φ*=M-1F，

(5)

式中：φ*为结构等效振型向量；F为由式(1)得到的各侧向力组合模式向量。

将式(4)代入式(3)中可以得到相应的等效振型质量系数α*，进而得到等效SDOF体系的谱加速度：

(6)

式中：Vb为结构基底剪力。

根据归一化的等效振型和等效振型参与系数，可得位移谱中：

(7)

(8)

2 考虑高阶振型影响的输电塔抗震性能评估方法

基于上述考虑高阶振型影响的能力谱分析原理，可以建立考虑高阶振型影响的输电塔抗震性能评估方法，基本流程如图2所示，主要计算步骤包括：

图2 考虑高阶振型的输电塔抗震性能评估流程Fig.2 Flowchart of seismic performance evaluation of transmission tower considering higher modes

① 根据几何参数、材料与力学参数、荷载与边界条件，建立输电塔分析模型。

② 进行模态分析，由式(1)～(3)组合结构不利方向的各振型侧向力组合模式，形成能力曲线(Vb-ur曲线)。

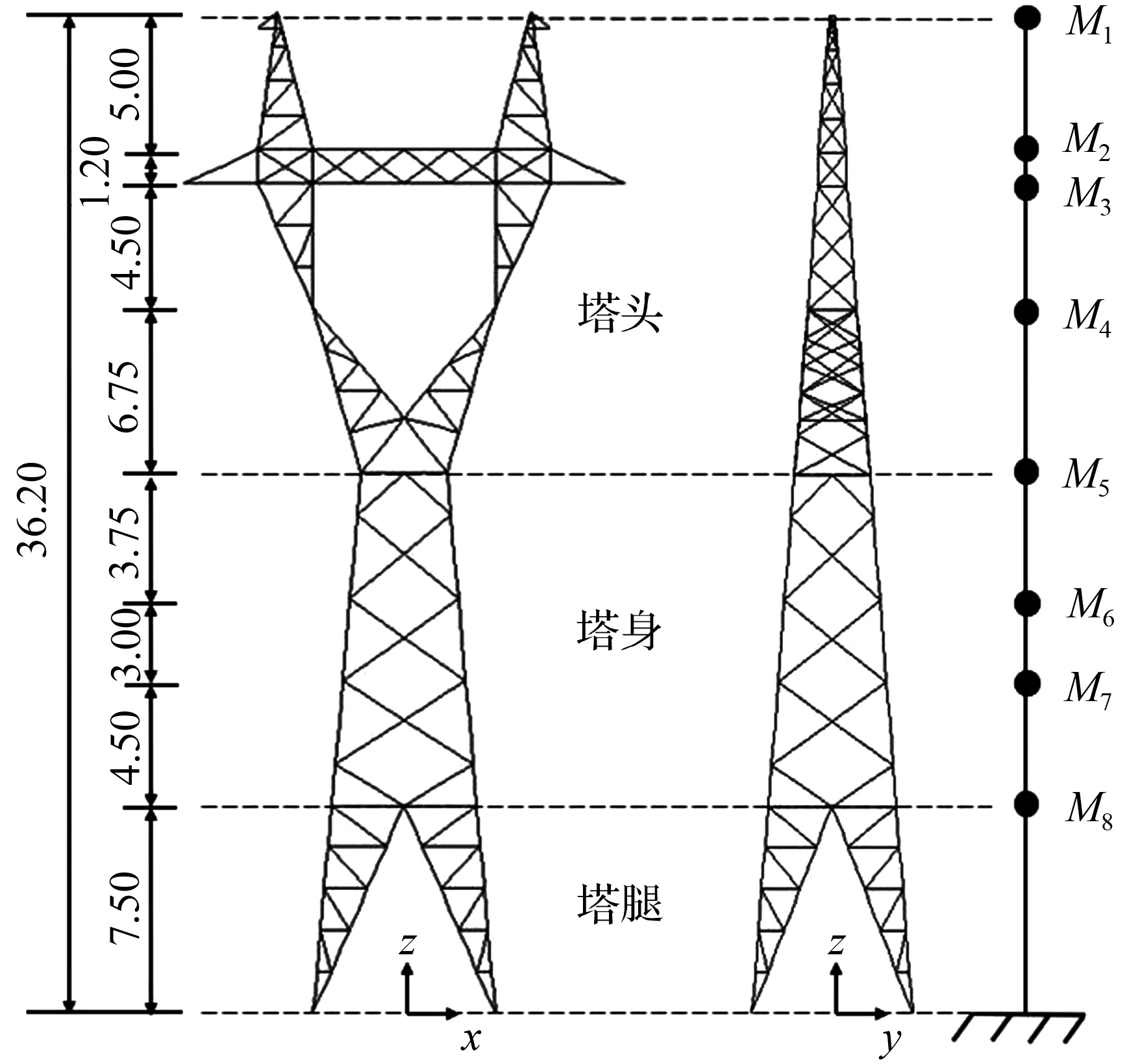
图3 酒杯型直线输电塔(单位：m)Fig.3 Model of wine-cup-type transmission tower

③ 采用式(5)和(3)分别求解出对应于各侧向力组合模式的等效振型向量φ*和等效振型质量系数α*，由式(5)～(8)形成输电塔的能力谱曲线(Sa-Sd曲线)。

④ 建立不同地震影响下需求谱曲线，并确定输电塔的各抗震性能点处水平位移ur。

⑤ 与各性能水平量化指标限值[ur]相比，判断输电塔是否满足抗震目标要求。若不满足，则需调整输电塔刚度和强度。

3 输电塔的抗震分析模型

3.1 输电塔的计算模型

如图3所示，某实际工程的220 kV直线酒杯型输电塔位于8度区的Ⅱ类场地，设计地震分组为第2组。该塔呼高为30 m，总高为36.2 m，根开为6.6 m，采用500 m水平档距和550 m垂直档距。构件主材采用Q345角钢，斜材与辅助材采用Q235角钢，角钢截面几何参数如表1所示。钢材的弹性模量为2.0×105MPa，密度为7 850 kg/m3，泊松比取0.3，阻尼比取0.02。采用通用有限元分析软件ANSYS进行结构分析，构件均采用空间梁单元Beam189，塔脚处固定约束，考虑结构自重、风荷载和地震组合作用，材料采用理想弹塑性本构模型。

表1 角钢截面几何参数Tab.1 Dimensional parameters of angle steel

3.2 输电塔的振型侧向力组合模式

根据输电塔的模态分析，可以得到如表2所示的输电塔自振特性参数，分析可知，输电塔的第一振型以x向振动为主，为结构不利方向，故本文主要考虑从x向输入的地震作用。为了合理选取对结构反应起最主要控制作用的振型阶数，本文根据振型贡献系数Rj值选取振型。输电塔的振型贡献系数Rj的分布情况如图4所示。分析可知，在前10阶振型中，第1和第8振型对结构x向的地震响应起到最主要的贡献作用，振型贡献系数Rj分别为100 %和52.3 %，其他振型贡献系数Rj均在10 %以下，对结构地震响应的影响相对较小，故本文选取第1和第8两阶振型，即x向振动第1和第2振型，进行侧向力组合，相应的2种侧向力分布如图5所示，同时也给出倒三角和多振型侧向力分布模式。

表2 自振特性参数Tab.2 Vibration characteristic parameters

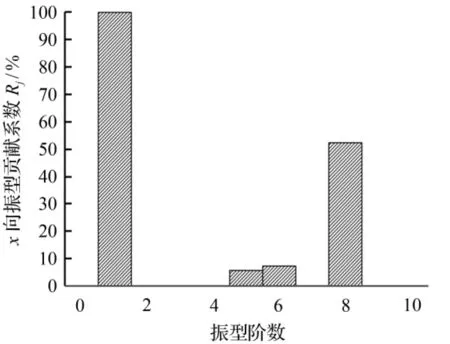
图4振型贡献系数
Fig.4ModalContributioncoefficients

图5侧向力分布模式
Fig.5Lateralforcepatterns

由图5可见，考虑高阶振型影响的两种侧向力组合模式与传统侧向力分布模式有所不同。其中，侧向力组合模式1与倒三角分布模式在结构底部相差不大，但在中部和顶部相差较大，而与多振型分布模式在结构中部较为接近，在结构底部和顶部有一定的差别；侧向力组合模式2与其他三种加载模式大小及加载方向均相差较大。

3.3 时程分析的地震动输入

为验证本文考虑高阶振型的能力谱分析的合理性，将开展结构动力时程分析(IDA)。根据《电力设施抗震设计规范》(GB 50260—2013)[25]规定，当抗震设计引入IDA分析时，应选取不少于三条地震波且至少应有一条人工合成地震波。因而，本文根据结构所处场地条件和地震烈度等条件，采用对应于50年内超越概率为10 %的12条美国PEER强震记录数据库中实际地震波和6条拟合人工波。从图6可知，实际地震反应谱均值、人工波反应谱均值与阻尼比为2 %的规范反应谱基本一致，具有良好的代表性。

(a) 地震动记录加速度反应谱

图6地震反应谱
Fig.6Responsespectraofgroundmotionrecords

4 输电塔的抗震性能分析

4.1 输电塔的能力谱曲线

将图5中两种侧向力组合模式施加在图3直线酒杯型输电塔的计算模型上进行Pushover分析，得到图7所示的结构能力曲线，图中也同时给出倒三角分布、多振型分布和IDA计算结果。同时，本文以IDA分析结果为参照，采用能力曲线偏差系数[26]研究不同侧向力模式下Pushover分析的能力曲线误差：

(9)

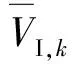
由图7可知，侧向力模式1的能力曲线位于其他侧向力模式之上，并与IDA分析结果较为接近。图8给出了各侧向力分布Pushover能力曲线的能力曲线偏差系数，侧向力模式1和倒三角分布的能力曲线偏差系数分别为5.3 %和11.2 %，侧向力模式2和多振型分布的能力曲线偏差系数达25 %以上。由此说明，本文侧向力模式1能较好地分析输电塔的抗震性能，后续将采用侧向力模式1进行结构性能分析与评估。

4.2 输电塔的侧向变形分析

为了检验本文侧向力组合模式的合理性，给出了罕遇地震下性能点处输电塔关键点的水平位移和层间位移角，如图9所示，图中也同时给出倒三角分布、多振型分布和IDA计算结果。由图9可知，本文侧力组合模式下各关键点处的水平位移和层间位移角均与IDA中位值偏差较小，分析结果明显优于其他侧向力分布。说明本文侧力组合模式能较好地反映输电塔抗震性能。此外，图9(a)中输电塔水平位移随着高度的增加而增大，但水平位移变化较为平缓，说明输电塔的抗侧移性能良好。图9(b)中输电塔在中部和顶部的层间位移角较大，表明该结构损伤主要集中在结构的中部和顶部，其中该结构的中上部结构处出现结构最大层间位移角，参照罕遇地震作用下结构弹塑性层间位移限值[27]，最大层间位移角值为1/237<[θp]=1/50，该输电塔满足弹塑性变形要求。

图7能力曲线
Fig.7Capacitycurves

图8能力曲线偏差系数
Fig.8Capacitycurvediscrepancyfactor

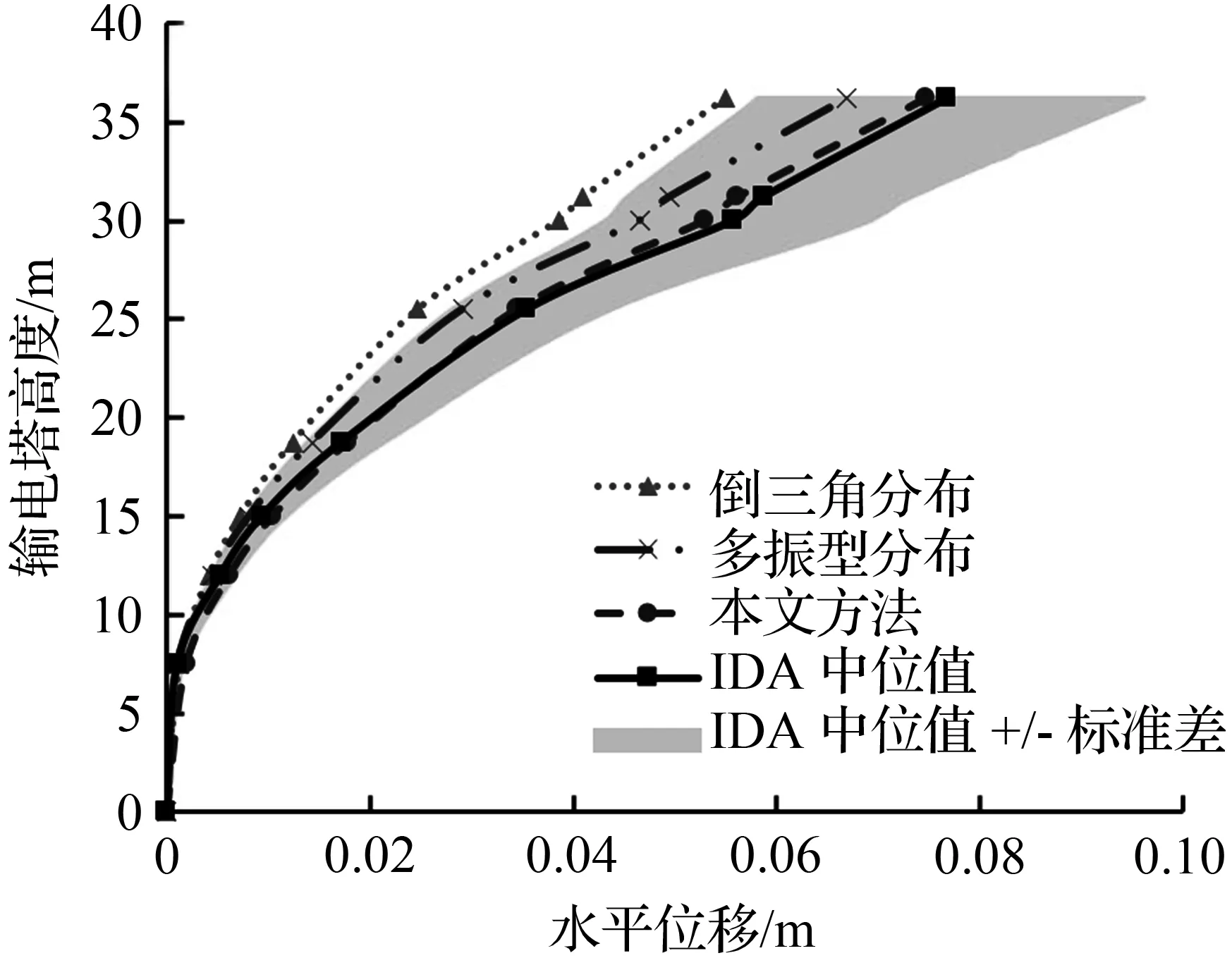
(a) 水平位移

图9性能点处结构关键点的位移响应
Fig.9Comparisonoftargetdisplacementatperformancepoint

4.3 输电塔的抗震性能评估

为了综合评估输电塔的抗震性能，本文选取输电塔的抗震目标为：在8度设防烈度的多遇地震、偶遇地震和罕遇地震作用下，输电塔应分别满足轻微破坏、中等破坏和严重破坏的性能水平要求。通过将本文侧力组合模式分析得到的能力谱曲线与需求谱曲线叠加在同一张ADRS图中，可获得如图10所示的不同地震影响下的性能点，从而结合输电塔性能点处水平位移和前期输电塔性能评估研究的性能水平量化指标[20]可得到如表3所示的结构抗震性能评估结果。分析可知，在8度设防烈度的多遇、偶遇、罕遇地震作用下，输电塔性能点处水平位移分别为0.014 2 m、0.042 6 m和0.074 7 m，均小于相应的抗震性能水准限值，满足抗震目标要求。

图10 不同地震作用下性能点计算Fig.10 Calculation of performance point under different earthquake actions

地震类别性能水准性能点[Sd/(m·s-2), Sa/m]性能点处结构响应(ur/m, Vb/kN)是否满足相应地震影响的性能水准多遇地震正常使用(ur < 3 h/1 000)(0.009 5, 1.70)(0.014 2, 18.8)ur<0.108 6,满足要求偶遇地震构件未屈服(ur

5 结论

结合振型侧向力组合法和能力谱法，提出了一种可以有效考虑高阶振型影响的输电塔抗震性能评估方法，并结合工程实例进行了验证分析。根据分析结果，可以得出以下结论：

① 以增量时程分析法的能力曲线为基准，本文方法的偏差系数为5.3 %，而倒三角和多振型侧向力分布的偏差系数分别为11.2 %和27.8 %，说明本文方法的计算精度更高。

② 与倒三角和多振型侧向力方法相比，由本文方法求解的地震水平位移、层间位移角与增量时程分析法中位值间的偏差更小，说明本文方法能够有效考虑高阶振型对输电塔抗震性能的影响。

③ 由于输电塔具有高耸、柔度大的特点，所以考虑高阶振型的影响能够更准确地获得不同地震下输电塔的性能水平，进而结合性能水平量化指标，可以更有效地评估输电塔的抗震性能。