补偿灰色周期外延模型诊疗预测方法研究*

张忠林 贾茹阁△ 张 静

本文提出了一种BP神经网络补偿灰色周期外延模型的预测方法,通过BP神经网络对灰色周期外延预测模型的残差序列进行修正,来提高预测精度,使预测值与原始值更吻合。实验分析了甘肃庆城区的诊疗情况,结果表明改进的算法适用于处理的预测对象,并且能较大幅度提高模型的预测精度。

资料与方法

1.资料来源

对地区性门诊人数进行建模预测,能够为政府以及相关医院制定相应工作计划提供决策理论依据,为了更加直观地说明补偿灰色周期外延模型在诊疗人次预测的具体过程,本文采用的数据为甘肃省庆城区某年1～12月门诊人数。

2.研究方法

(1)建立灰色GM(1,1)预测模型:

①设有原始序列:X(0)={x(0)(1),x(0)(2),…,x(0)(n)}

(1)

其中x(0)(k)≥0,k=1,2,…,n

对原始序列做一次累加:

X(1)={x(1)(1),x(1)(2),…,x(1)(n)}

(2)

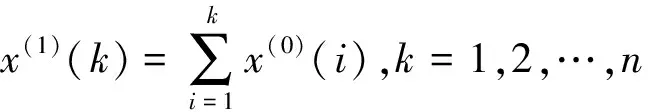
②X(1)={x(1)(1),x(1)(2),…,x(1)(n)}满足单变量常微分方程:

(3)

其中-a为发展系数,b为灰色作用变量。

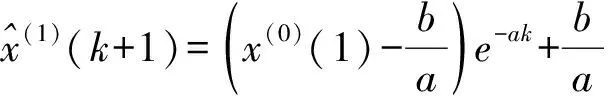
(4)

根据最小二乘法求得系数a和b:

[a,b](-1)=(BTB)(-1)BTY

(5)

其中:Y=[x(0)(2)x(0)(3) …x(0)(n)]-1

③把求得的a和b代入式(4)中的影响方程:

(6)

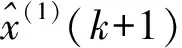
(7)

(2)残差序列

根据上述灰色预测模型结果得到其残差序列:

(8)

(3)建立残差序列的周期外延模型

①残差序列x′(k)的均值生成函数。其计算公式如下:

(9)

式中,n为样本序列长度,nm为小于n/m的最大整数,M为小于n/2的最大整数。

fm(k)=xm(k),k=i[mod(m)],k=1,2,…,n

(10)

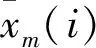
②提取优势周期

检验序列x′(k)是否存在隐含长度为m的周期,有如下公式:

F(m)=(n-m)S(m)/((m-1)S),其为服从自由度(m-1,n-m)的F分布。

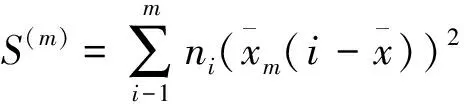
(11)

(12)

(13)

事先设定一个置信水平a,如果F(m)>Fa(m-1,n-m),则认为此序列存在隐含长度为m的优势周期。

③序列x′(k)减去周期m对应的延拓函数,构成新的序列,表示为x″(k)=x′(k)-fm(k),然后再对新的序列x″(k)重复步骤(2)、(3),再次提取优势周期。

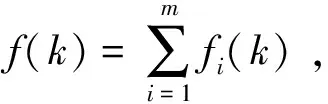
(4)BP神经网络修正残差

首先,采用收集好的序列数据对模型进行训练。其次,通过不断调整神经网络各单元的权重,减小误差,当误差达到预先设定好的精确度时便完成训练。此时,实际值和预测值非常接近。训练完成的模型便可用来进行预测。本文采用新陈代谢预测法,具体描述为:先设定好参数,再将连续3个月的门诊数据作为模型的输入序列,第4个月的预测值为输出值;随后输入序列中每次会加入1个新的数据,舍弃最前面的1个数据。本研究中,以1月～3月的数据预测4月数据,以2月～4月数据预测5月数据,依次类推,逐步预测。12月的数据用来检验改模型,若检验合格,则可用来预测未来5个月门诊人数。图1为BP神经网络结构图。以上工作均在Matlab R2014a软件中实现,具体实现流程图如图2所示。

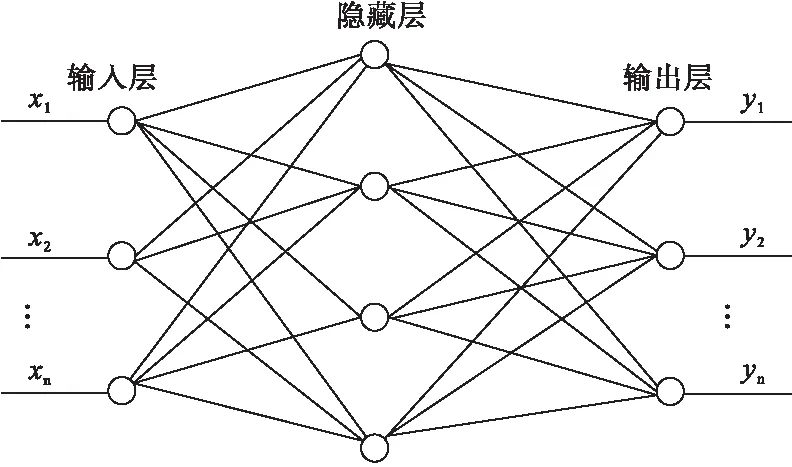
图1 BP神经网络结构图

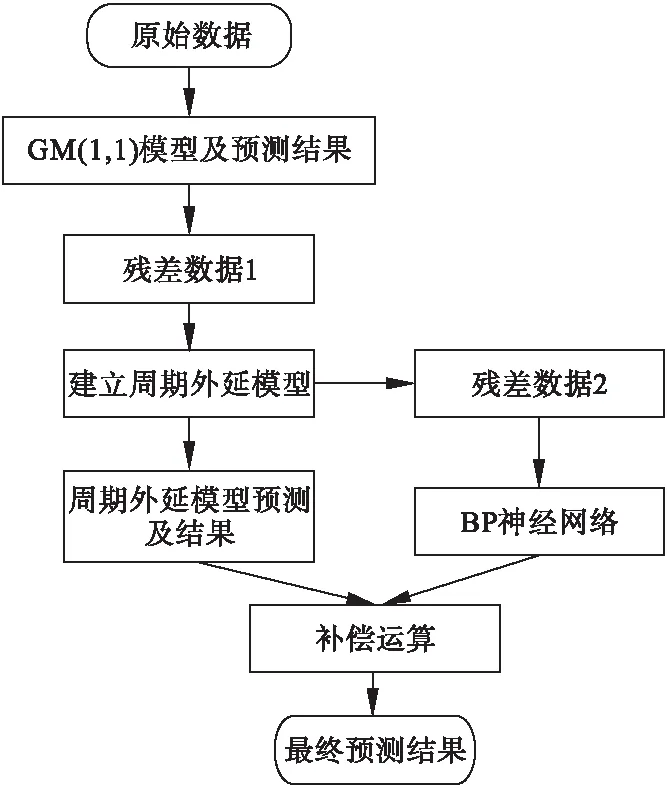
图2 BP神经网络补偿模型预测流程图

其相关参数设置如下:

①三层网络:输入层,S型隐含层,线性输出层。

②各层节点数:输入层3;隐含层9;输出层1。

③训练函数为trainoss:一步分割法,它是共轭梯度法和拟牛顿法的一种折中方法。该算法每次迭代所需的存储量和计算量也介于这两种算法之间。

④其他参数:特征参数3个,学习率0.01;训练次 数100;均方误差0.001。

结 果

1.仿真预测及模型的检验情况

经计算,预测样本序列的平均相对误差为1.1892%,用12月的数据检验该模型,结果表明12月份的门诊人数为2.4254万,而实际门诊人数为2.4312万,其相对误差为0.2386%,预测值与原始值拟合度较高。

由表1和图3可以看出,单纯地使用GM(1,1)模型时结果只具有变化的总体走向(增长趋势),而灰色周期外延模型则考虑了序列的周期波动性,对原始数据的周期性变化进行分析,在一定程度上提高了精度和准确性,但其预测精度还有待提高。本文在此基础上采用神经网络对周期外延模型的预测误差进行修正,使预测结果更靠近原始值,预测精度更高。其中,GM(1,1)模型预测结果的平均相对误差为6.6487%,灰色周期外延模型预测结果的相对误差为6.1211%,相比于GM(1,1)模型有所提高。而本文提出的BP神经网络补偿周期外延模型预测结果的平均相对误差为1.1892%, 将近前两种预测结果的6倍,且每个预测精度均小于5%，说明本文提出的方法预测精度高,适用性好。

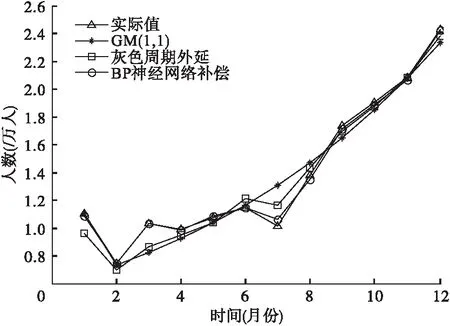
图3 三种模型预测结果比较图

由表1和图4可知,GM(1,1)模型、灰色周期外延模型和BP神经网络修正这三种模型的预测误差均在可接受范围内,我们分别用这三种模型来对诊疗人次数据做预测,可以看出:本文模型的预测精度要大大高于其他两种方法的预测精度,而且其误差曲线相对其他两种较平稳,波动幅度小,说明其预测效果佳。因此当原始数据具有一定的趋势性以及明显的周期变化特点时,采用本文提出的方法进行预测,可以准确把握诊疗人次的未来趋势,且预测精度较高。

2.对未来5个月门诊人数的预测

利用本文建立模型和方法,可以得到甘肃省庆城区未来5个月的诊疗人次分别为:1.0881万,0.7446万,1.0324万,0.9849万,1.0838万。

讨 论

地区诊疗人次是反映地方性管理经营状况的重要指标,对其动态变化进行客观、 准确的分析和预测,可对地方医院提供科学有效的管理方法。目前对门诊人数常用的预测模型有灰色模型、马尔科夫链模型、神经网络模型以及各种组合模型等。灰色模型[1]所需样本量小且不需有规律性分布,模型简单易操作,适合稳定的短期预测[2]。近年来一些学者在初值优化[3]、灰导数[4]、背景值[5]等方面对GM(1,1)模型进行了改进,丰富了灰色系统理论的研究,并将其应用于经济管理、疾病预测等诸多领域[6],也有部分学者将灰色理论与灰色周期外延模型[7-8]、神经网络模型[9-10]等相结合,以提高预测精度。马尔科夫链模型是一种适用于随机波动的动态预测方法,但预测结果的准确性会因划分不同状态而受影响[11]。

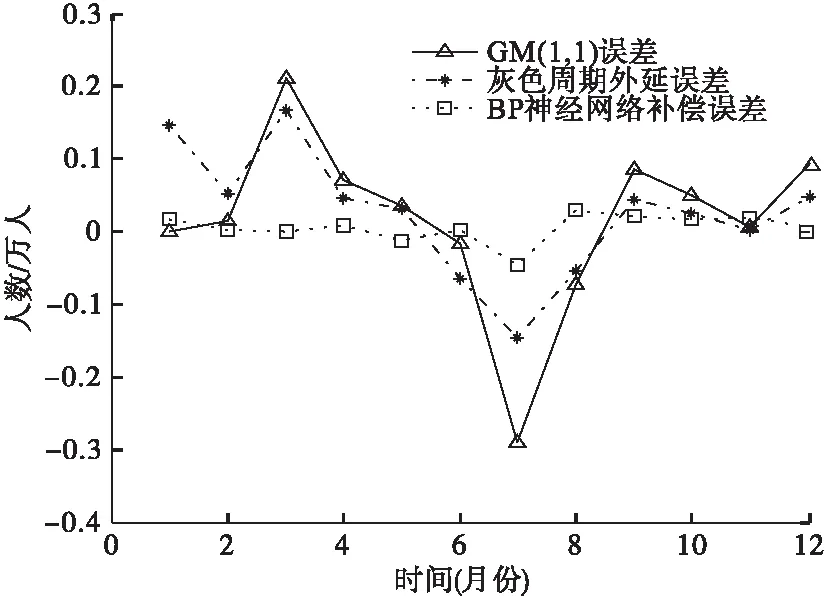
图4 三种模型预测误差比较图

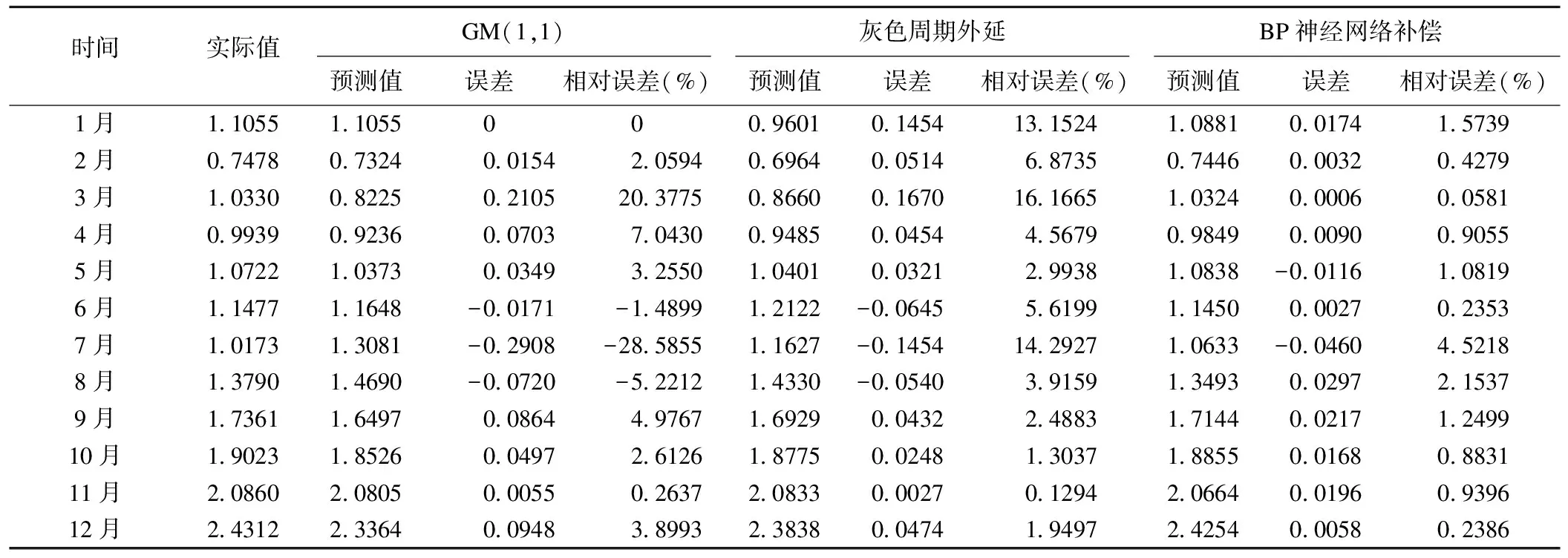
表1 三种模型预测结果比较

BP神经网络模型能够处理复杂的大规模数据,从而被广泛地应用于门诊和住院等方面的预测。它能描述许多复杂的非线性相关性,学习和存贮大量的输入输出模式映射关系,无需满足先验知识、正态性、线性及独立性等各种条件[12]。因此本研究采用BP神经网络补偿修正残差的方法,在灰色周期外延模型预测的基础上,利用神经网络对灰色周期外延模型的预测误差进行校正,既保持了原始序列的周期性和波动性,也提高了预测精度,并采用此方法对甘肃省庆城区某年的门诊人数进行了探讨研究。结果表明仅使用灰色模型和周期外延模型得到的相对误差分别为6.6487%、6.1211%,而本文方法得到的平均相对误差为1.1892%,并且预测误差均小于5%。本文方法通过分析诊疗人次的历史数据,可以掌握其动态变化规律,发现医院运营过程中的问题,调整部署经营策略;也可为流行病学研究人员提供有效的依据和理论研究方法。