基于两条生存曲线间面积的非参数统计推断方法研究*

黄兴辉 陈金宝 杨紫荆 吕晶晶 侯雅文 陈 征△

在医学临床研究中,组间生存率差异的检验是常见的研究问题之一。Log-rank检验[1]是目前最常用的方法,其在风险率成比例假定成立时具有较高的检验效能,但当不满足比例风险假定,特别是两条生存曲线交叉时,交叉点前后生存率高低逆转可能导致正负差异相互抵消,从而使Log-rank检验的检验效能大幅降低。为此,Pepe和Fleming[2]提出了一类加权Kaplan-Meier检验,它通过两组Kaplan-Meier估计值的累积加权差来构建统计量,同时已有研究表明[3],当风险率交叉时,加权Kaplan-Meier检验的检验效能比Log-rank检验高。对此Lin[4]提出一种基于两条生存曲线间面积值大小来构造统计量的面积检验法,不管风险率是否成比例、生存曲线是否交叉,其统计量构造均不受影响,避免了交叉点前后正负差异相互抵消的问题;然而在原假设下其检验统计量假设服从标准正态分布,但经作者模拟研究发现,该检验法一类错误偏离预设的检验水准,且其统计量呈非正态性,检验结果可靠性受到影响。本文基于置换检验思想,对原面积检验法[4]进行校正,得到置换面积检验法,用两条生存曲线间面积值大小构造统计量,利用置换重抽样技术得到相应的拒绝域,而不依赖于统计量原始分布,从而校正了面积检验法统计量呈非正态性的问题;同时通过模拟研究和实例验证分析,对置换面积检验法、Log-rank检验、加权Kaplan-Meier检验和面积检验法进行性能比较。

方法介绍

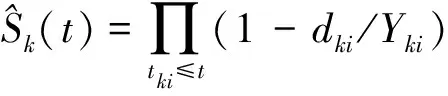
比较两组间生存率的差异,原假设是在任意时刻t上,两组对应的生存率相等,即H0:S1(t)=S2(t),备择假设为:H1:S1(t)≠S2(t)。

1.面积检验法

将两条生存曲线之间的绝对面积值大小作为衡量差异的指标[4],根据上述面积指标定义可以将其表示为:

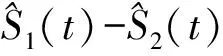
利用正态近似的原理,面积指标Δ均值和方差可以分别估计为:

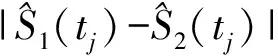
2.置换面积检验法

置换重抽样的思想是根据所研究的问题构造一个检验统计量[5],并利用原始样本,按照排列组合的原理,构造检验统计量的理论抽样分布;然后求出从该分布中获得原始样本及更极端样本的概率(P值),并界定此概率值,由此作出推论。在原假设下,本文通过计算检验统计量Δ*的偏度系数和峰度系数[6],同时结合正态性检验验证Δ*的正态性;并且将面积检验法和置换思想结合提出一种置换面积检验法,通过999次重抽样过程得到Δ*的拒绝域。置换面积检验法对原始数据分布不作要求,从而校正面积检验法统计量不服从正态分布而导致影响检验稳定性的问题。

具体步骤如下:

1.建立原假设、备择假设;

2.将两组原始生存数据混合起来,进行无放回重抽样,并且计算检验统计量Δ*(1);

3.重复第2步999次,依次计算得到Δ*(2),Δ*(3),……Δ*(1000);

4.计算双侧概率P值:p=sum{|Δ*(n)|>|Δ*|}/1000。

模拟研究

本文采用Monte-Carlo模拟来比较Log-rank检验、加权Kaplan-Meier检验、面积检验和置换面积检验法的检验效能和I类错误,并且评价各种检验方法的稳健性和适用性。检验效能的比较分下列三种类型[3,8-9](包含六种模拟情形):(1)组间风险率满足成比例假定(图1A);(2)两条生存曲线部分发散:前中期发散(后期收敛)(图1B);两条生存曲线后期发散(前中期收敛)(图1C);(3)两条生存曲线交叉:生存曲线交叉于前期,交叉点约位于S(t)=0.6～0.8(图1D);生存曲线交叉于中期,交叉点约位于S(t)=0.4～0.6(图1E);生存曲线交叉于后期,交叉点约位于S(t)=0.2～0.4(图1F)。一类错误中两组生存时间均由参数为0.25的指数分布产生,在每一种参数下都模拟设置了删失比例为0%、15%、30%、45%的情形,同时考虑了均衡设计(N1=N2=20,50,100)以及非均衡设计(N1=20,N2=50;N1=50,N2=100)对各种检验方法统计性能的影响。

每一个参数组合下模拟1000次,显著性水平α=0.05。首先产生服从于某一特定分布(如分段指数分布、威布尔分布)生存时间X,当无右删失时,记录生存时间T=X,状态δ=1;当右删失存在时,两组删失时间C分别由服从于U(0,a)和U(0,b)的均匀分布产生,记录生存时间T=min(X,C),δ=I[X≤C](称I(·)为指示函数);并通过设定参数a和b的值控制每组平均删失比例。

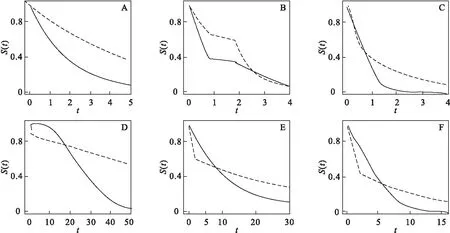
图1 模拟类型图

1.面积检验法统计量服从正态性的问题

在原假设下得到不同样本量、删失率组合下的检验统计量Δ*,分别计算其偏度系数和峰度系数,同时结合Shapiro-Wilk正态性检验判断检验统计量是否服从于正态分布。通过模拟研究发现,在5种样本量与4种删失率的不同组合下:其检验统计量的偏度系数最小值和最大值分别是1.033、1.436(正态分布偏度系数为0),峰度系数最小值和最大值分别是1.206、3.290(正态分布峰度系数为3),提示检验统计量呈右偏态;并且Shapiro-Wilk正态性检验结果显示在不同样本量和删失率组合下检验统计量均不服从正态分布(P<0.001)。

2.I类错误和检验效能

由于模拟研究中样本量、删失率以及模拟类型组合较多,为了更清晰展示一类错误率和检验效能,以及方便总结模拟结果,本文利用方差分析技术[10],建立以下四个模型。模型构造的思想为:在考虑控制了其他多余影响因素下,研究主要影响因素对检验法的影响。比如模型1,在控制删失率(CENSORE)、不同模拟情形下(SITUATION),研究不同样本量(NUM)组合下各种检验法的表现(模型2、模型3同理);对于模型4,控制所有影响因素,单纯看各种检验方法的表现。I类错误评价指标:结果变量Y减去尺度水平0.05再乘以100,即评价指标为平均偏差值,方法表现越好其期望E(Y)越接近于0;检验效能评价指标:结果变量Y为平均拒绝率,即评价指标为平均拒绝率,方法表现越好则其期望E(Y)越大。

模型1:E(Y)=TEST×NUM+CENSORE+SITUATION

模型2:E(Y)=TEST×CENSORE+NUM+SITUATION

模型3:E(Y)=TEST×SITUATION+CENSORE+NUM

模型4:E(Y)=TEST+SITUATION+CENSORE+NUM

表1反应一类错误的结果,面积检验的I类错误偏离预设的检验水准,而基于置换面积检验法以及其他几种检验法的I类错误均在0.05左右轻微波动,其中加权Kaplan-Meier检验相对保守;整体来看,删失比例和不同样本量组合对I类错误影响不大。

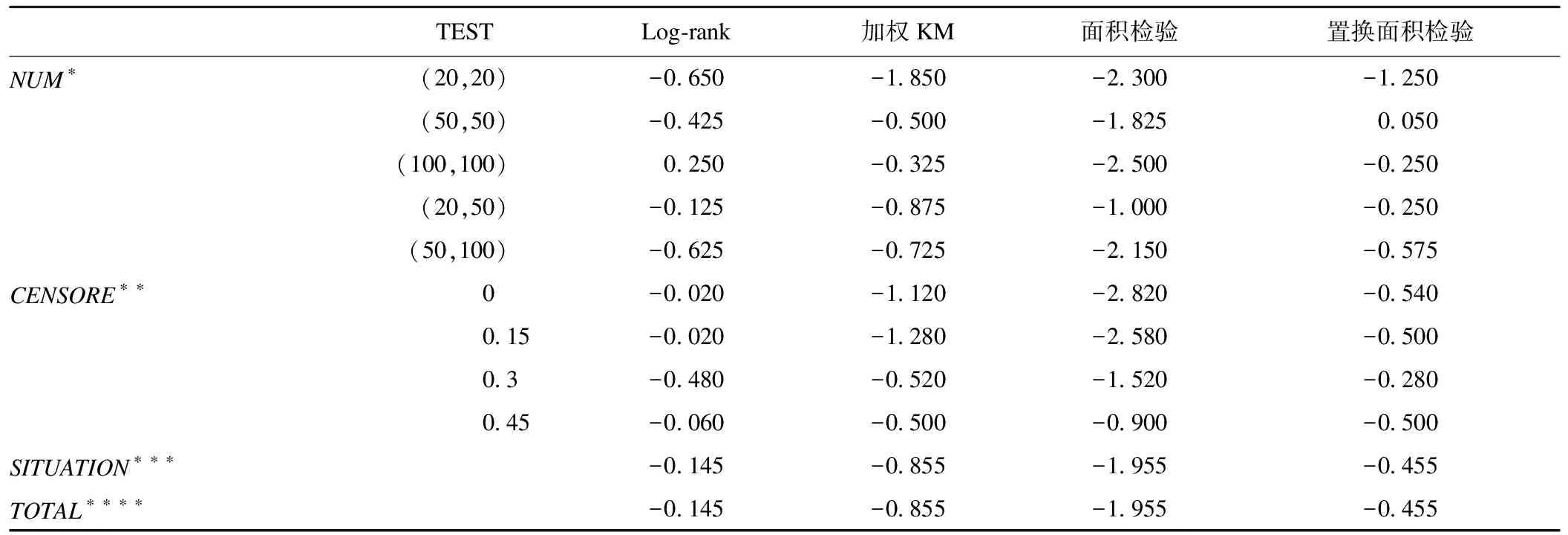
表1 四种检验方法的一类错误(平均偏差值)

检验效能的结果展现在表2,随着样本量增大,各检验方法的检验效能均有所提高;随着删失率增大,面积检验法以及置换面积检验法的检验效能都呈下降趋势,而Log-rank检验、加权Kaplan-Meier检验均在删失率为45%时出现反转;情形A时,即成比例,各检验法的检验效能均在0.7以上,Log-rank检验表现最佳;情形D时,即生存曲线交叉于早期,面积检验和置换面积检验的检验效能最高;其它所有情形下,B、C、E、F,即生存曲线前中期发散(后期收敛)、后期发散(前中期收敛)、生存曲线交叉于中期或后期,置换面积检验法的检验效能均最高。

综合一类错误(表1)和检验效能(表2),样本量是否均衡对五种检验法的影响不大;置换面积检验法与其它检验法相比,既较好地控制了I类错误,又在生存曲线交叉、生存曲线部分发散(收敛)时提高了检验效能,特别是组间风险率成比例假设失效或生存曲线交叉时具有较高效能。

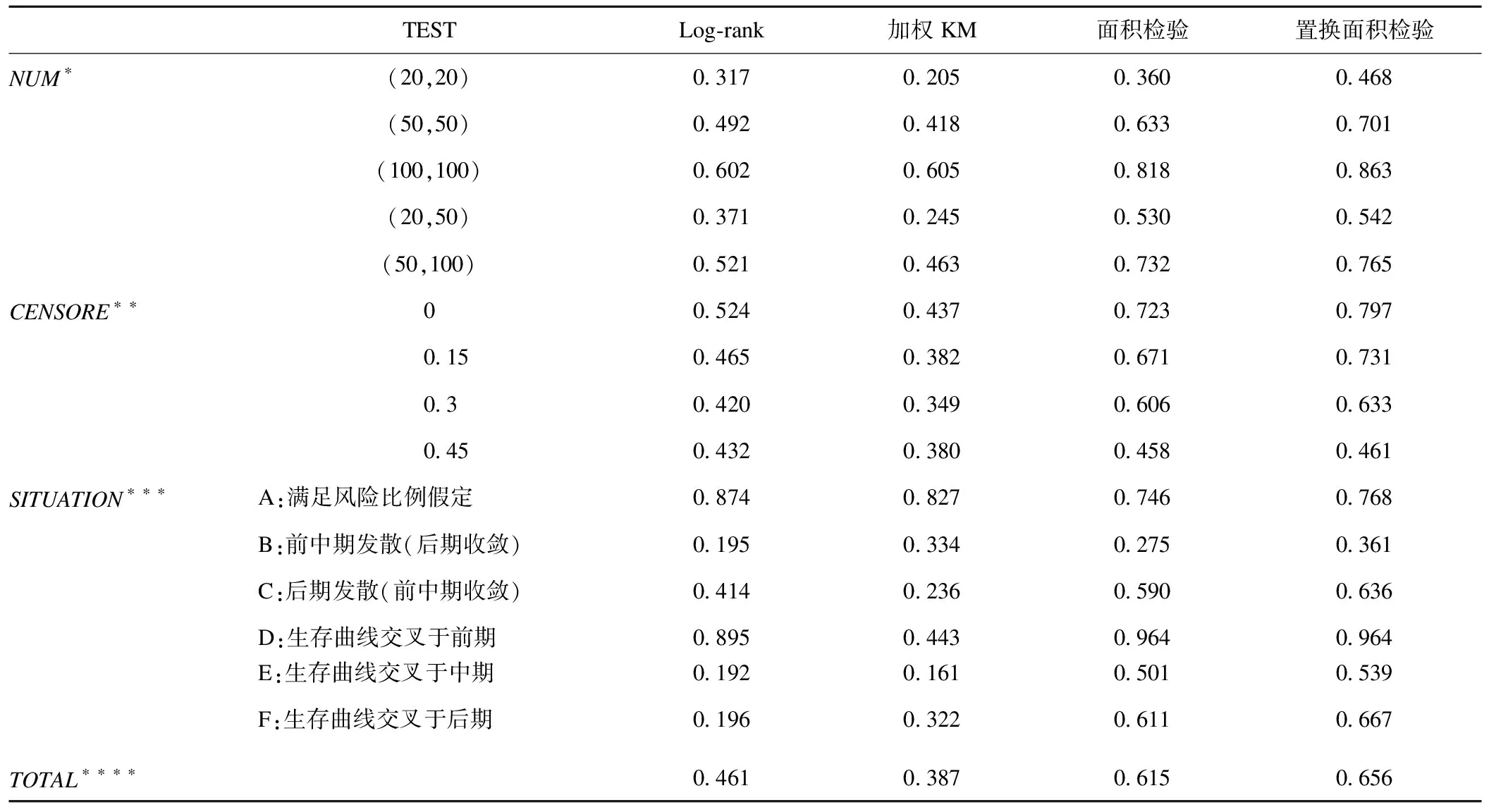
表2 四种检验方法的检验效能(平均拒绝率)

实例分析

实例一(风险率成比例):在一项两种药物对治疗膀胱癌患者疗效的临床试验中[11],共收集340例患者,其中安慰剂组纳入188名患者,噻替派组纳入152名患者,两组删失率分别为38.3%和26.3%,终点事件为出现膀胱癌复发,到研究截止时间尚未发生终点事件为右删失。经Grambsch-Therneau检验得到组间风险率成比例假定有效(χ2=0.07,P=0.789),其生存曲线见图2A。两组疗效的差异检验显示,Log-rank、加权KM、面积检验、置换面积检验的P值均小于0.05,提示噻替派的治疗效果优于安慰剂组,具体结果见表3。

实例二(成比例假设失效且生存曲线交叉):一项两种药物(吉非替尼、卡铂-紫杉醇)治疗肺腺癌的临床研究中[12],共收集1217例患者,其中吉非替尼组纳入患者609例,卡铂-紫杉醇组纳入患者608例,两组删失率分别为25.6%和18.3%,主要终点事件为恶化或者死亡,到研究截止时间尚未发生终点事件为右删失。由于原文数据无法获得,因此参照Royston[13]的方法模拟产生了本例两组样本量均为100的模拟数据。图2B显示在中位生存期附近(S(t)=0.5,约随访至第6个月)两条生存曲线出现明显交叉,并经Grambsch-Therneau检验得到组间风险率成比例假定失效(χ2=10.00,P=0.002),置换面积检验结果(P=0.042)提示两种药物(吉非替尼、卡铂-紫杉醇)治疗肺腺癌的效果有统计学差异,与此相反Log-rank、加权KM、面积检验的结果均显示差异无统计学意义(P>0.05)。由于生存曲线出现交叉,从图2B直观发现交叉点前卡铂-紫杉醇组生存率可能高于吉非替尼组,但卡铂-紫杉醇不能提供长期疗效,在约第6个月后发生逆转,吉非替尼组生存率可能会高于卡铂-紫杉醇组。因此进一步比较短期和长期(交叉点前、后)两组生存率的差异,随访至第6个月的Log-rank检验结果提示短期上两组差异无统计学意义(χ2=0.272,P=0.602),而对于交叉点后的时期,基于二次型χ2检验[14]结果(χ2=4.098,P=0.043)发现从长期角度看,吉非替尼组能提供更好的疗效。

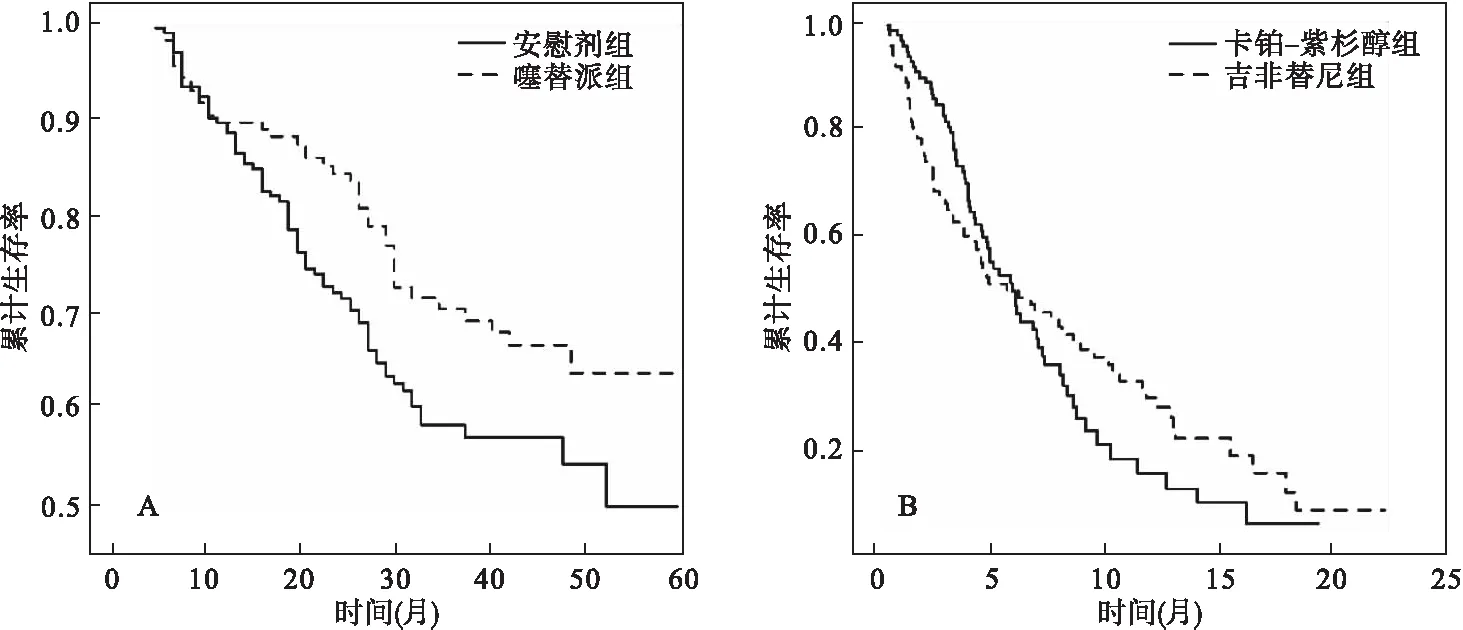
图2 实例的生存曲线图(A:实例一,B:实例二)

表3 四种检验法在实例一、二的应用结果

讨 论

在删失率为45%的时候,Log-rank检验、加权Kaplan-Meier检验的检验效能出现反转,而其他检验法的检验效能均下降,考虑到情形D(生存曲线交叉于前期)、情形F(生存曲线交叉于后期)时,随着删失率升高到一定比例时,可能在模拟中出现生存曲线不交叉或者近似成比例的情况,从而导致Log-rank检验、加权Kaplan-Meier检验的检验效能在删失率为45%时出现反转。

本文将置换思想与面积检验法结合起来,在多个样本量和删失率组合下,既能够较好的控制I类错误,又在面积检验法的基础上,提高了检验效能,与其他几种检验方法相比,综合表现较优;置换面积检验法可以用两条生存曲线间的面积直观反映两组生存率的差异大小,不管成比例假定是否成立,生存曲线是否交叉均能适用。因此本文建议当两条生存曲线满足比例假定时,首选Log-rank检验法;而当两条生存曲线风险率成比例假设失效,特别是生存曲线出现交叉时,推荐更稳健的置换面积检验法。