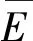平面四索驱动并联机构的零点标定方法

郭晓玲,汤奥斐，张 奔

(西安理工大学机械与精密仪器工程学院，陕西西安710048)

索驱动并联机器人是由柔索代替刚性连杆的一种新型并联机构，具有工作空间大、承载能力强、累计误差小、易拆卸、可重构等优点，在加工制造、航空航天、医疗机械等领域得到广泛应用[1]。

定位精度是索驱动并联机器人的重要性能指标之一，对于实现末端执行器的精确操作具有重要意义。索驱动并联机器人定位误差主要分为两类：一类是系统误差，如加工误差、装配误差、传动误差等；另一类是随机误差，如数字误差、环境误差、负载误差等。

研究表明，几乎95%的机器人位置误差都是由于机器人内部运动学模型不准确引起的[2]，从而有必要对机器人进行运动学标定。

鉴于末端执行器所有的操作任务是相对于坐标系零点位置的相对运动，零点位置的准确程度直接决定机器人的定位精度。因此，减小零点误差对提高机器人定位精度具有重要意义。

目前，对于零点误差，国内外的解决方法主要有机械调整法和零点标定法两种。其中，零点标定技术方面的研究较少，大多仍停留在理论研究和实验阶段[3]。Ding等[4]应用几何误差迭代及非线性拟合方法，对一种2自由度并联机器人的零点误差进行了辨识；郭云鹏等[5]运用空间矢量法建立了6自由度并联平台的零点误差模型，借助激光跟踪仪完成零点标定，提高了精度；隋春平等[6]以Delta并联机器人为例，提出一种基于视觉测量的零点标定方法；梅江平等[7]针对一种4自由度高速并联机器人Cross-IV的零点标定问题，提出了一种基于末端转角误差信息的快速零点标定方法。

本文针对平面四索驱动并联机构，提出一种简单快速的零点标定方法，首先根据运动学逆解建立零点误差模型并建立目标函数；然后通过直角尺、千分表、磁力表座等标准量具采集测量点的坐标；接着，利用非线性最小二乘法对实验数据进行处理，完成零点标定，并对实验结果进行分析。

1 误差模型

1.1 结构模型

四索驱动并联机构的结构示意图如图 1(a)所示，该机器人系统由四个位于地面的电机同时驱动四个独立的卷索机构，每个卷索机构上的柔索通过架设在静平台四个顶点上的定滑轮牵引动平台运动。四索驱动并联机构的连接图如图 1(b)所示，其中，全局坐标系为O-XY，其原点位于矩形B1B2B3B4的中点，OX方向为水平方向，OY方向为竖直方向；局部坐标系为O′-X′Y′，其原点位于动平台的中心点，当动平台位于矩形B1B2B3B4的中点时，局部坐标系与全局坐标系重合。

索与定滑轮的切点为Bi(i=1,2,…,4)，索与动平台的连接点为Ai(i=1,2,…,4)，已知模型参数a=50 mm，b=1 120 mm。

由矢量封闭原理得，四索驱动并联机器人的索长Li(i=1,2,…,4)为：

Li=|OBi-OAi|

(1)

式中：在全局坐标系O-XY下，OBi为柔索与静平台连接点的位置矢量；OAi为柔索与动平台连接点的位置矢量。

此外，四根索的初始索长分别为L01、L02、L03、L04。卷索机构中的滚筒结构简图如图 2所示。

已知电机旋转一圈对应的脉冲数M=8 192，滚筒直径D=50 mm，则一个脉冲对应的索长LM=πD/8 192=0.02 mm。因此，四根索的索长变化量ΔLi便可由脉冲变化ΔMi求得：

ΔLi=LM×ΔMi(i=1,2,…,4)

(2)

则索长Li为：

Li=L0i+ΔLi=L0i+LM×ΔMi(i=1,2,…,4)

(3)

图1 四索驱动并联机构结构简图Fig.1 Structure diagram for four-cable-driven parallel mechanism

图2 滚筒结构简图Fig.2 Roller structure diagram

1.2 误差模型

四索驱动并联机构要实现精确控制，首要问题就是找到初始零点的准确位置。

设全局坐标系O-XY的原点O(x0,y0)为初始零点，为了找到它的准确位置，现对其进行标定。

首先，建立如图 3(a)所示的测量坐标系O′-X′Y′。

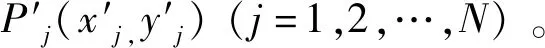
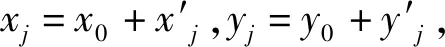
Li,j=|OBi-OAi,j|

(i=1,2,…,4;j=1,2,…,N)

(4)

式(4)中方程组的个数为4N，其中包含2N+4个未知量。若方程有解，根据方程个数和解的关系有4N≥2N+4 ，即N≥2 ，因此测量点的个数至少为2。式(3)相应改写为：

Li,j=L0i+ΔLi,j=L0i+LM×ΔMi,j

(i=1,2,…,4;j=1,2,…,N)

(5)

图3 零点标定示意图Fig.3 Diagram for zero-point calibration

由式(4)和式(5)可得，目标函数索长误差E：

(6)

2 误差测量

测量时，首要问题是确定测量坐标系的基准轴线，才能保证测量数据的准确。本文利用标准直角尺的两条相互垂直的边来确定测量坐标的轴系，如图 4所示。

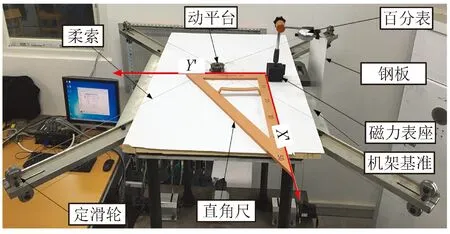
图4 测量坐标系的选择Fig.4 Selection of measurement coordinate system

前期准备工作：

姥姥没接她的茬。反正也不是什么大不了的事，当年全是我做的主，今天我就再做主一次，也不跟你爸你妈商量了，全告诉你吧。

1) 因为静平台加工精度高，故选择静平台上与全局坐标系X轴平行的边作为测量坐标系X′轴的基准，在基准面处固定一块与XOY平面垂直且与X轴平行的钢板；

2) 标准量具磁力表座的底面平面度较高，沿着直角尺一条直角边滑动，磁力表座上的百分表与钢板接触。

具体操作为：

首先，使直角尺与X轴平行的一条边与磁力表座紧密接触；

然后，记录磁力表座沿着直角尺的直角边滑动过程中百分表的读数，即间接获得直角尺与基准面的偏差，由于本文的测量精度为0.1 mm，故在滑动过程中百分表显示的偏差在0.1 mm以内视为定位准确；

接着，不断调整直角尺的位置，磁力表座在400 mm(最大实验值)之内移动的过程中，其百分表的读数偏差在0.1 mm以内，即说明直角尺一条直角边所在位置为测量坐标系的X′轴，且与参考基准面平行；

同时，由于直角尺为标准量具，直角尺的另一直角边确定为测量坐标系的Y′轴，此时，直角尺两条边便组成了测量坐标系O′-X′Y′[8]。

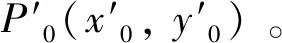
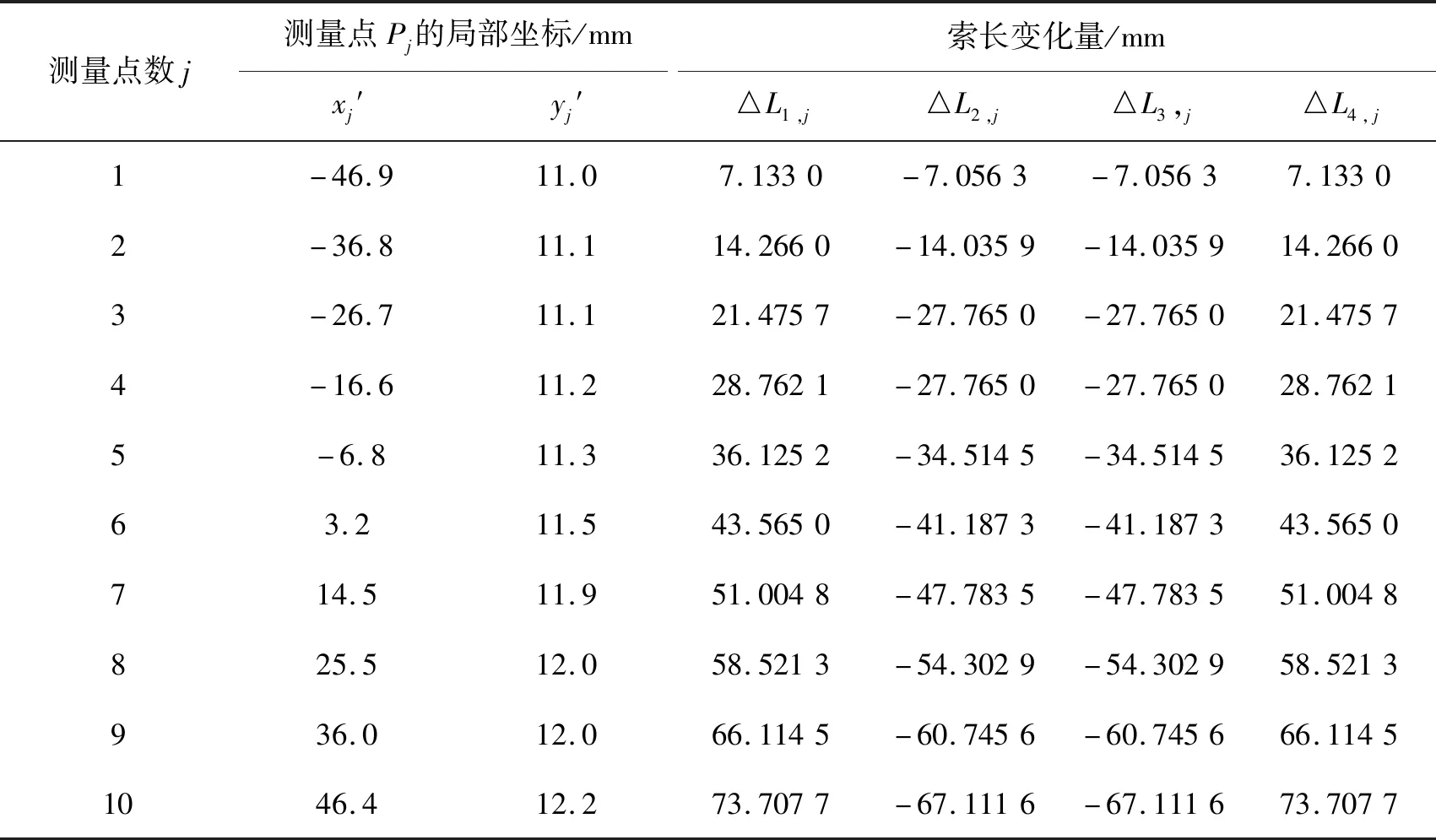
表1 零点标定实验数据Tab.1 Experiment data from zero-point calibration

3 参数识别与误差补偿

测量点的坐标采集后，运用最小二乘法进行数值计算，求出满足式(6)目标函数的最优解。求解过程中，先求解出目标函数的雅克比矩阵，再使用迭代法求出零点位置。

现将静平台和动平台坐标代入式(6)中求出第i根索索长误差，则式(6)变为：

Ei(x,y)=(bix-aix-x)2+(biy-aiy-y)2
(i=1,2,…,4)

(7)

式中：bix、biy为第i根索与静平台连接点的坐标；aix、aiy为第i根索与动平台连接点的坐标；x、y为动平台P的坐标位置。

对式(7)求其雅克比矩阵：

(8)

由于最小二乘法一般对初值的选取要求较高，这里选择零点附近的值作为初值，即动平台零点在测量坐标系下的初值P0坐标为：x0=-85.0 mm，y0=38.0 mm；初始索长(即标定零点位置对应的索长)为：L01=L02=L03=L04=756.60 mm。

(9)

给定迭代收敛精度ε=10-3mm，若存在：

(10)

则满足收敛条件；否则继续迭代，迭代增量为：

ΔP=-J+F

(11)

Pk+1=Pk+ΔP

(12)

式中：F为外力螺旋；Pk为第k次迭代的坐标，k的取值由式(10)的迭代结果确定；J+=(JTJ)-1JT。

标定算法的计算过程如图5所示，其为第i根索最小二乘法标定流程图。

通过上述方法，经4次(索编号i分别取1、2、3、4)计算后，标定后的零点坐标为：x0=-82.94 mm，y0=38.89 mm。

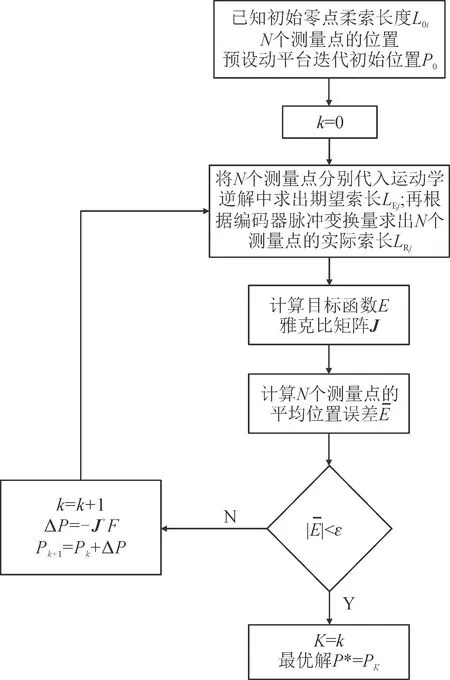
图5 最小二乘法标定Fig.5 Least-squares calibration method

图6 迭代计算误差Fig.6 Iterative calculation error

4 结 语