非配对设计多值有序资料多水平多重Logistic回归分析

凤思苑，李长平，2，胡良平

（1.天津医科大学公共卫生学院卫生统计学教研室，天津300070；2.世界中医药学会联合会临床科研统计学专业委员会，北京100029；3.军事科学院研究生院，北京100850*通信作者：胡良平，E-mail：lphu812@sina.com）

1 基本概念

1.1 多值有序资料

“多值有序”资料特指因变量或结局变量为多值有序变量（例如在描述药物或手术疗效时经常用“治愈、显效、好转、无效和死亡”作为一个主要疗效指标的不同取值），而自变量没有任何的限制，可以是定量的或定性的（包括二值的、多值有序的、多值名义的）变量。

1.2 多水平的概念

在社会科学研究中，“社会”的基本概念是一个具有分级结构的整体。所谓的分级结构就是指较低层次的单位嵌套在较高层次的单位之下，而这种社会分级结构自然而然的使其产生的数据呈现多层次（多水平）结构［1］。例如，在对学生成绩的研究中，认为学生的学习成绩或状态不仅与个人的内在因素有关，还与所处的环境（学校、班级）有关，因此，在研究学生成绩与个体水平变量的数量关系时，还需将其嵌套到相应的学校和班级中去。由此形成3个层次的结构数据：第一个层次的观察单位是学生，第二个层次的观察单位是班级，第三个层次的观察单位是学校。这里的“多水平”是指层次结构数据中的多个层次，其中学生为低水平即水平1单位，班级为中水平即水平2单位，而学校则为高水平即水平3单位；而在通常的回归分析中，只有一种观察单位，那就是“个体”或“受试对象”。此时，若资料中出现了“学校”“班级”等变量，则它们就被视为定性的“影响因素”（即自变量），通常需要将它们产生哑变量后引入回归模型中去［2］。

1.3 多重logistic回归模型

多重logistic回归模型是一种广义线性回归模型，适用于研究一个定性因变量与多个自变量之间的依赖关系，其因变量y可以是二值变量、多值名义变量或多值有序变量。它不同于一般的多重线性回归模型，其本质属于非线性概率回归模型，在这种回归模型中，真正的因变量是y取某特定值时所对应的概率［如P(y=0)或P(y=1)］。

2 数据结构

【例1】研究者选择8所医院开展多中心临床试验，每所医院均选取400名受试者，在各医院内随机等分成两组，分别接受试验药物和对照药物治疗，治疗结果为多值有序变量（好、一般、差），试比较两种药物的疗效。基本信息见表1。

表1 多中心临床试验的基本信息

3 回归模型的构建与求解

3.1 模型的构建

分析结局变量为多值有序变量时，一般构建累积logistic回归模型，也称为比例优势模型。累积logistic回归模型其实就是结局变量为二值变量的logistic回归模型的扩展，从潜在变量的概念出发，模型可定义如下：

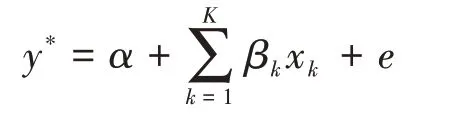
其中y*表示观察现象的内在趋势，不能被直接测量；e为误差项。当实际的观测结果变量有J个不同的类别时（j=1，2，…，m，…，J），相应的取值即为y=1，y=2，…，y=J。于是，（J-1）个分界点将相邻各类别分开［3-4］。

与结局变量为二值变量的logit变换类似，logit变换后的累积logistic回归模型表达如下：

在该模型中，P（y≤m|x）实际是结局变量取值≤m的累积概率，即为P（y=1|x）+P（y=2|x）+…+P（y=m|x）的概率之和。该模型是将结局变量的J个等级人为分成两类｛1，2，…，m｝和｛m+1，…，J｝，在这两类基础上定义的logit函数，实为前m个等级的累积概率与后（J-m）个等级累积概率比值的对数。该模型中共有（J-1）个累积的logits，β0m是第m个logit的截距，βk是协变量xk的斜率。模型的一个重要特征就是（J-1）个截距互不相同，但每个logit中相同自变量的系数相同，故而又称比例优势模型［1，4］。

多水平累积logistic回归模型是对固定效应和随机效应做了更细致的考察，其模型可以表达如下：

该公式与普通的（单水平）累积logistic回归模型相似，对应了（J-1）个logit，但不同的是：此处的每个logits的截距可能是随机系数，因而可体现宏观水平（本例为2水平）单位间的差异。公式中的X是含有固定斜率的协变量的设计矩阵，β代表固定效应，而Z是含有随机斜率的协变量的设计矩阵，U代表随机效应［1，3-4］。

3.2 模型的参数估计和假设检验

多水平累积logistic回归模型由于存在水平1和水平2残差组成的复合残差结构，模型的参数估计较为复杂，需同时估计固定回归系数、随机回归系数以及矩阵G和R的方差/协方差矩阵（矩阵G为水平2残差的方差/协方差矩阵、矩阵R为水平1残差的方差/协方差矩阵）。目前SAS的GLIMMIX、NLMIXED过程进行参数估计的方法主要有RSPL、MSPL、RMPL、MMPL，其本质都是基于最大似然的估计方法。

多水平累积logistic回归模型的假设检验包括固定效应的假设检验、随机效应的假设检验以及模型比较的检验。固定效应即模型中的固定参数包括总体的截距、协变量的斜率。随机效应是指模型中的随机部分，主要指宏观水平（本例为2水平）残差的方差/协方差。当采用不同的模型拟合相同的数据时，可以用似然比检验，有关的统计量有-2倍的对数似然值。当模型中包含的参数数目相同时，-2倍的对数似然值越小，模型对数据的拟合效果越好。

4 SAS程序及结果解释

4.1 SAS程序

【程序说明】程序共3步，包括1个数据步和2个过程步。首先建立例1的数据集MLMO，利用do循环语句输入变量Hospital（医院编号）、Drug（药物类型）、Gender（性别）和结局变量y（疗效类型）。程序第2步调用GLIMMIX过程运行多水平累积logistic回归模型，其中Class语句创建分类变量Hospital，model语句中设置y为响应变量，“dist=multi”和“link=clogit”选项分别设定分布为多项式分布，连接函数为累积logit函数。Random语句用来设定随机效应，“type=chol”选项采用chol-esky分解法来设定G矩阵，目的是保证G矩阵具有正特征根，以保证模型参数估计的稳定。程序第三步利用NLMIXED过程实现多水平累积logistic回归模型，parms语句给出模型中有关参数的初始值，此处初始值为由GLIMMIX过程计算所得。z为定义的线性预测值，由固定效应部分和随机效应u组成。

4.2 主要输出结果及解释

以下为GLIMMIX过程方差/协方差参数估计的结果，给出了随机效应方差的估计值。其中随机截距的方差（即）的估计值为0.4447，标准误为0.1243。但此处未给出随机截距方差是否为0的假设检验结果，故不能判断与0之间的差异是否有统计学意义，尚不能说明是否存在随机效应。

以下为GLIMMIX过程输出的固定效应检验结果。模型有两个截距，这是因为响应变量疗效有三个水平。在响应变量为J个水平的多水平累积logistic回归模型中，有（J-1）个logits函数式，这些函数式中有（J-1）个不同的截距，但会有一组相同的协变量系数的估计值。因模型是以“y=1”为基础，故截距值-0.4714表示协变量均取0值时治疗结果为“好”的对数发生比；截距值为0.7312表示协变量均取0值时治疗结果为“好”和“一般”的对数发生比［注意：疗效单独为“一般”的截距应为“0.7312-（-0.4714）=1.2026”］。正（负）斜率表示治疗效果为“好”的可能性高（低）。例如，Drug的斜率为0.3627（P＜0.0001），表示试验组药物的治疗效果为“好”的概率比对照组药物治疗效果为“好”的概率高［1，5］。此外，还可以在程序中model语句的“/”之后添加选项oddsratio获得各个协变量的OR估计值及95%CI。

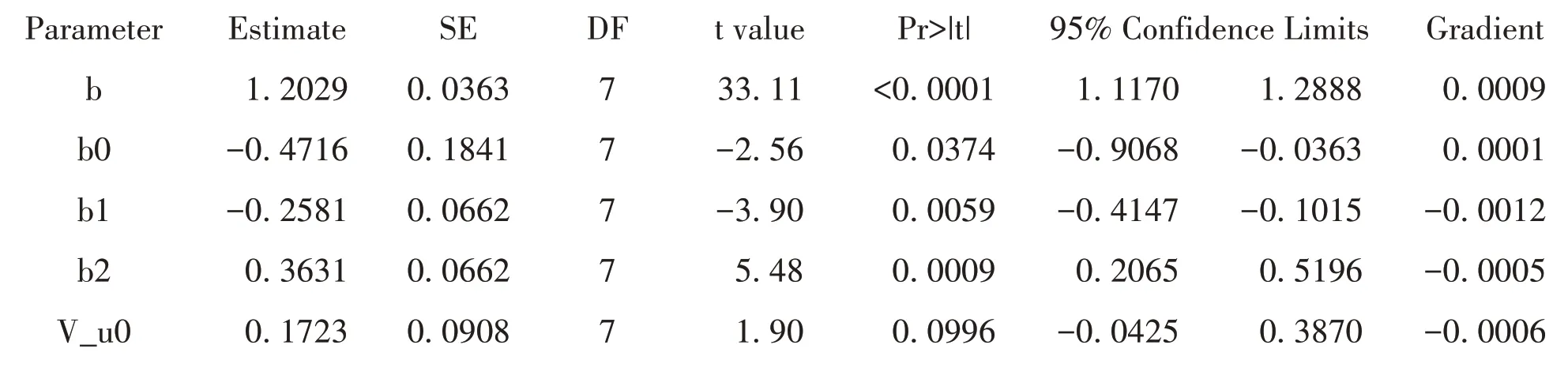
NLMIXED过程输出了与GLIMMIX过程类似的结果，即模型的总体信息、优化信息以及迭代史，其中重要的是模型各参数的初始值信息：b0为模型的总体截距，b1为性别的效应，b2为药物的效应，V_u0为随机效应的方差，这些参数的设定来源于GLIMMIX过程计算结果。NLMIXED过程模型的初始参数如下：

以下为NLMIXED过程输出的模型的拟合信息和参数估计，包括固定效应和随机效应方差的参数估计以及相应的假设检验结果。其中b0、b+b0、b1和b2分别表示截距1、截距2、Gender和Drug的系数值。对于随机效应的假设检验，这里进行的是双侧检验。实际上，由于方差不可能为负值，所以检验残差方差应选用单侧检验，故此处的V_u0对应P值除以2后才是正确的P值，实际小于0.05，说明确实存在随机效应。有关其他固定效应参数的解释参考GLIMMIX过程输出结果的解释。当然，由于NLMIXED过程所得的结果提供了随机效应的假设检验，更为精确，最终结果应以NLMIXED过程的输出结果为准。

5 讨论与小结

对非配对的多值有序资料建立logistic回归模型时，除了要考虑有充足的样本量，以保证参数估计的稳定性，还必须考虑研究个体是否存在聚集性特征。目前医学研究试验设计大多数会产生多层次（即多水平）数据，而此类数据常存在组内相关的问题，即组内观察值相互间是非独立的。这种现象的存在会导致自变量和结局变量的关系随着宏观水平单位的不同而变化，此时若依然采用一般的累积logistic回归模型，会导致错误的参数估计结果，而多水平累积logistic回归模型可以很好地解决组内同质、组间异质数据的回归建模问题。

本文就多水平多值有序数据分别利用SAS的GLIMMIX过程和NLMIXED过程来拟合多水平累积logistic回归模型，结果发现两个过程参数估计的结果极为相似，但仍存在一些区别：NLMIXED过程的参数估计结果中直接提供了随机效应的假设检验结果，有利于模型对于随机效应的取舍，若随机效应检验的结果没有统计学意义，可以直接采用普通的累积logistic回归模型直接拟合数据。GLIMMIX过程并不提供该检验，但却为NLMIXED过程的初始参数设置提供了参考，极大地缩短了模型拟合的速度。建议二者同时使用，但以NLMIXED过程的输出结果为准。

采用多水平累积logistic回归模型分析数据时还需要注意以下问题。①测量中心化：在多水平累积logistic回归分析中，要注意同时关注水平1截距和斜率的变化。因为假定一个水平1截距为1.30的回归模型，我们可以说当模型中所有自变量都为0时，某种结局的对数优势比为1.30。但是所观察的某些解释变量若没有实际的零值，则上述解释便无任何实际意义。此种情况下要使截距变得有意义，必须通过中心化重新定义或转化自变量的测量值［1］。②随机效应检验：模型随机部分的检验主要指对宏观水平残差的方差/协方差检验，根据定义，方差不能为负数，所以检验残差方差应选用单侧检验，其统计量相应的P值应除以2；其次，用于模型比较的似然比检验也可以用于随机效应的检验。即先将特定的水平1回归系数设定为固定系数，然后再将其设定为随机系数，分别拟合并比较以筛选出适宜的模型［1］。