GPS/GLONASS/BDS/Galileo系统载波相位观测值质量对比分析

刘琳, 席瑞杰

(1. 武汉大学 卫星导航定位技术研究中心,湖北 武汉 430079;2. 武汉大学 测绘学院,湖北 武汉 430079;3. 诺丁汉大学地理空间研究所,英国,诺丁汉郡 诺丁汉 NG7 2TU)

0 引 言

随着GPS、GLONASS系统的现代化及Galileo和BDS系统的不断完善,卫星导航系统已由单一的GPS系统发展为多系统并存的全球性卫星导航系统[1-2]．为了增强全球卫星导航系统(GNSS)在各个应用领域的服务能力,应尽可能充分利用这些丰富的卫星信号资源．通过对不同系统不同频率的GNSS观测数据进行质量分析与评估,可为观测数据选择、质量控制等方面提供有效信息[3],也是多系统组合应用中构建随机模型的重要依据．因此,对GPS/GLONASS/BDS/Galileo系统的原始观测数据进行质量分析具有重要意义,也是当前的研究热点之一[4-6]．

截止目前,已有部分学者对各系统观测数据质量进行了分析和评估[3-4,7-9]．一般可从载噪比、多路径、观测卫星数及DOP值等方面分析不同系统观测值质量[3,7],但仍难以反应观测数据的实际精度;为更真实地评估观测值质量,采用高度角加权模型和信噪比加权模型对相应观测值定权,且被广泛运用[4-5,8,10-11]．总体来说,目前对于四个系统各个频率的观测值质量分析的研究仍不够完善,全面系统地评估和对比四系统观测值单差残差及其质量随高度角的变化情况,对实际应用中各卫星系统观测数据的选择具有重要意义．

观测值的随机模型影响观测方程的参数估值及其质量评定[5]．目前,Gamit、Bernese等国际知名精密数据处理软件中仍采用经验高度角模型[6]．然而,随着多系统多频观测值应用的日益广泛,研究适用于各系统不同频率的随机模型十分重要．本文采用几何无关和M-W组合方法,基于科廷大学实测零基线数据计算了四系统的载波相位单差残差序列,并对比分析其在不同系统不同频率随高度角变化情况．同时,本文将该单差残差序列恢复为非差观测值均方根(RMS)序列,利用高度角随机模型中的正弦模型和指数模型对载波相位观测值精度随高度角变化情况建模,获得适用于不同系统不同频率观测值的随机模型．

1 数据处理方法

1.1 基于几何无关组合的单差函数模型

在零基线实验中,多路径效应、电离层误差等认为被完全消除,故可将其用于检验和评价接收机噪声[9]．对GNSS观测值的随机特性进行评估时,由于站间单差几何无关模型(SingleDifferenceGeometry-freefunctionalmodel)卫星之间无几何相关性,因此分析单颗卫星的观测值质量时比常用的双差模型适用性更好[4-6]．由于GNSS精密定位中主要使用载波相位观测量,因此本文仅对GPS(L1、L2)/GLONASS(G1、G2)/BDS(B1、B2)/Galileo(E1、E5a)四系统的双频载波相位观测值进行分析(以下均写作L1,L2)．

通常,单历元单频站间单差相位观测方程[4]表示如下:

λjΔφj=Δρ+esΔTj-λjΔNj+Δεφ,

(1)

为方便进行观测值精度估计,本文采用综合应用几何无关(GF)组合和M-W(Melbourne- Wubbena)组合的方法[4]来固定每颗卫星的站间单差模糊度．该方法具有无需参考星,能有效消除卫星钟差、距离相关项等优势,且适用于包括GPS、GLONASS、BDS、Galileo在内的多个卫星导航系统．载波相位单差GF和M-W组合方程[4]如下:

(2)

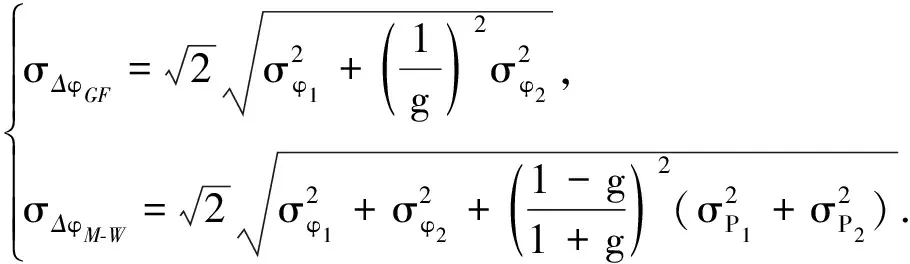
(3)

基于式(2),单差模糊度浮点解可表示为

(4)

其标准差表示如下:

(5)

(6)

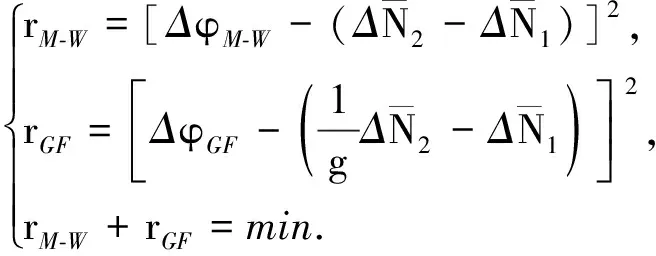
(7)

固定模糊度后,式(1)中只需估计参数ΔTj．采用最小二乘模型,误差方程如下:

v=Bx-l.

(8)

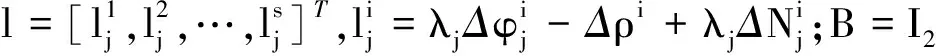
1.2 GF/M-W组合值平滑及粗差剔除

一般来说,某颗卫星在某一观测时段中未发生周跳,其单差M-W组合观测值应接近于某一常数;在电离层变化缓慢的情况下,单差GF观测值序列较为平滑[13]．考虑单差M-W组合观测值可能受较大伪距噪声影响而使模糊度固定不准确,本文采用如下方法对单差M-W/GF值进行周跳探测、粗差剔除及平滑．以M-W为例,第k个历元的单差M-W平滑值递推计算公式如下:

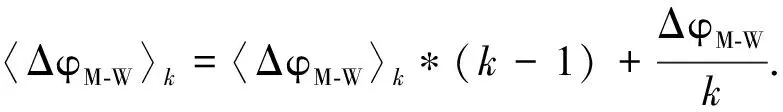
(9)

若在历元k有|〈ΔφM-W〉k-ΔφM-W(k)|〉3σΔφM-W,则认为该历元可能存在周跳或粗差,继续判断下一历元,若有|〈ΔφM-W〉k+1-ΔφM-W(k+1)|〉3σΔφM-W,判定k历元存在粗差,进行剔除;否则,计算两超限值之差,若差值小于阈值(设为1),认为历元k存在周跳,否则认为是粗差．遍历所有历元,得到平滑的M-W组合观测值．对GF观测值序列的平滑过程与上述处理方式相同．

1.3 非差观测值标准差计算

一般而言,在相对短的时间内(如几分钟)同一卫星高度角变化缓慢,可认为其观测值精度保持不变[5]．假定短时间内同时观测到s颗卫星,使用连续n个历元的观测数据计算第i颗卫星的非差观测值标准差[4-5],计算公式如下:

(10)

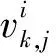
2 实验与结果分析

2.1 数据描述

本文实验采用澳大利亚科廷大学GNSS研究中心(The GNSS Research Centre of Curtin University)公布的实测零基线GNSS数据(http://saegnss2.curtin.edu/ldc/)进行对比分析．一般来说,接收机观测值质量由接收机内部噪声、测站环境、观测时刻卫星高度角等多方面因素影响[5]．本文数据采集所使用接收机为同型号接收机,可避免接收机端GLONASS系统各卫星频率间偏差的影响．因此,可用于分析GPS/GLONASS/ BDS/Galileo四个系统载波单差残差及观测数据质量随高度角的变化．

测站CUT0和CUT2位于南纬32°,东经115.9°,接收机类型为Trimble Net R9,天线类型为TRM 59800.00 SCIS,固件版本为5.10．本文采用该测站2018年年积日095天的数据(4月5日)进行计算,采样率为30 s,截止高度角设置为10°．

图1示出了CUT0测站2018年095天各个系统的卫星可见数随时间变化情况．由于BDS卫星系统现主要覆盖亚太地区,因此该站该天观测到的北斗卫星整体数量最多,除少数时间段外基本在9颗以上;GPS卫星略少,大部分时候也至少有8颗可见卫星;在同一时段GLONASS卫星最多可见9颗,最少可见5颗;而Galileo系统卫星可见数最少,部分时段最多可观测到6颗,大约20 h之后可见卫星数低于3颗,无法单独进行定位解算．经统计,同时观测四个卫星系统至少能接收到25颗卫星信号,增强了复杂环境下GNSS定位导航的可靠性和可用性[1-2]．

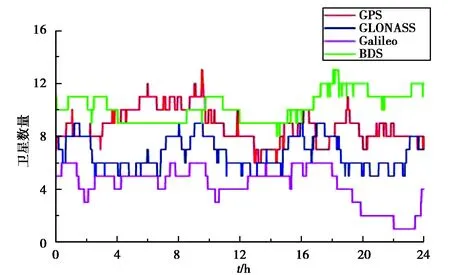
图1 CUT0测站2018年095天四系统卫星可见数序列

2.2 单差观测值残差与高度角相关性分析

北斗系统包含地球静止轨道卫星(GEO )、倾斜地球同步轨道卫星(IGSO)、中地球轨道卫星(MEO)三类卫星;由于GEO卫星相对地球静止,不适用于分析北斗卫星观测值随高度角变化的情况,因此将该类卫星B1、B2载波观测值单差残差序列单独列出,如图2所示．由图可知GEO卫星B1单差残差序列较B2序列质量稍好,而在B1、B2上各GEO卫星单差残差序列均在高度角范围内有一定角度的变化,最多变化3.5°,可能原因为摄动力等因素对GEO卫星轨道有一定影响[8]．

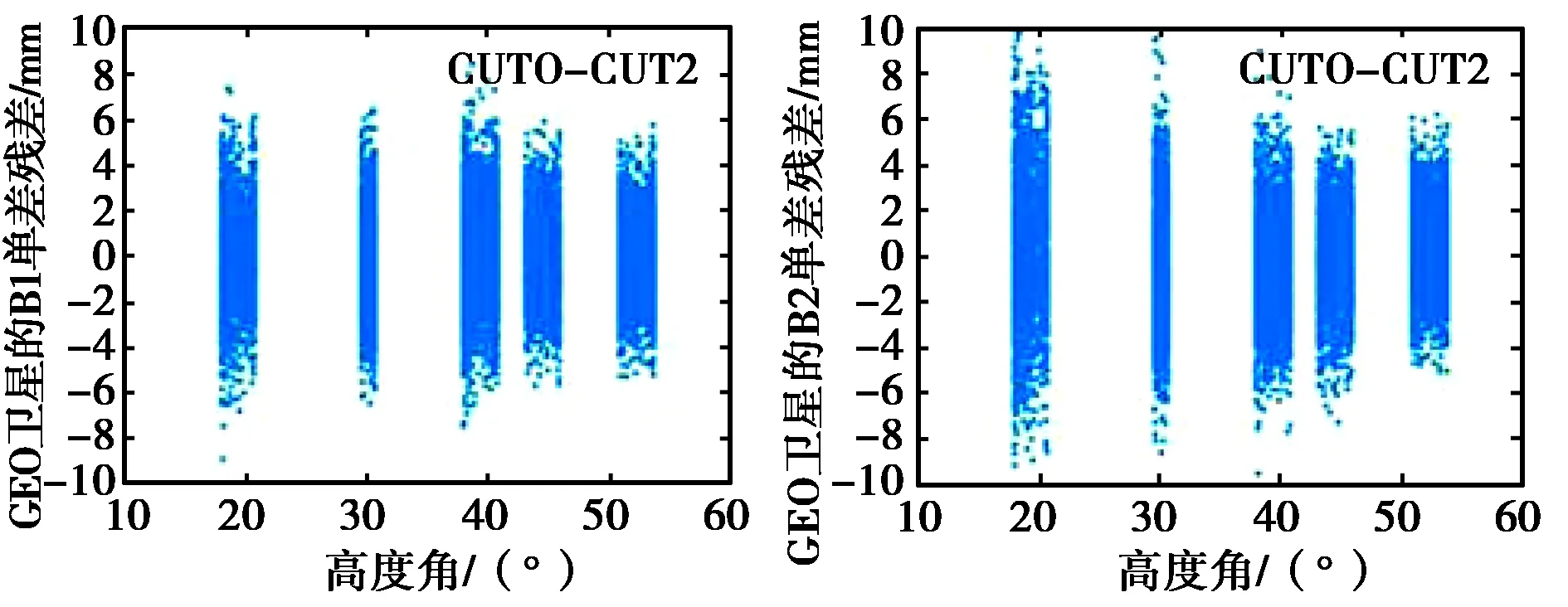
图2 GEO卫星B1、B2载波相位单差残差与高度角关系

图3、图4示出了各卫星系统2018年095天L1、L2载波相位观测值单差残差随高度角的变化情况,红色虚线为各系统各频率所有历元所有卫星标准差的±平均值．如图所示,四个系统L1、L2观测值单差残差序列均随高度角增大而有一定程度的收敛,直至趋于平稳;其可能原因为原始信号质量和接收机接收功率随着高度角变化而相应不同,从而使观测值单差残差发生变化．

同时,各个系统卫星观测值不同频率单差残差均与高度角相关,且残差序列在不同系统不同频率表现出不同性质．如图3所示,当高度角>20°,GPS与Galileo系统L1载波相位单差残差序列稳定,与高度角相关性不强,大部分残差在±3 mm范围内波动,Galileo观测值精度略差．GLONASS与Galileo的L1观测值精度相当,但残差序列随高度角变化更为敏感,在10°～25°间残差值相对发散．BDS系统单差残差序列随高度角变化也不显著,但整体精度超过1 mm,而其他三个系统的L1观测值精度均优于1 mm．

在L2频率上,Galileo观测值单差残差序列及精度则表现出最优特性,与L1单差残差和精度整体相当,其他系统L2单差残差值和精度与L1相比则有明显区别．GPS的 L2单差残差序列较L1序列波动幅度显著增大,尤其当高度角在10°～25°之间变化时;BDS的L2单差残差序列较L1则整体更为发散,大部分值在±4 mm范围内变化;两系统的L2载波观测值精度均在1.2 mm左右．GLONASS系统L2残差序列与高度角强相关,且在所有高度角范围内都很分散,观测值精度超过1.5 mm．

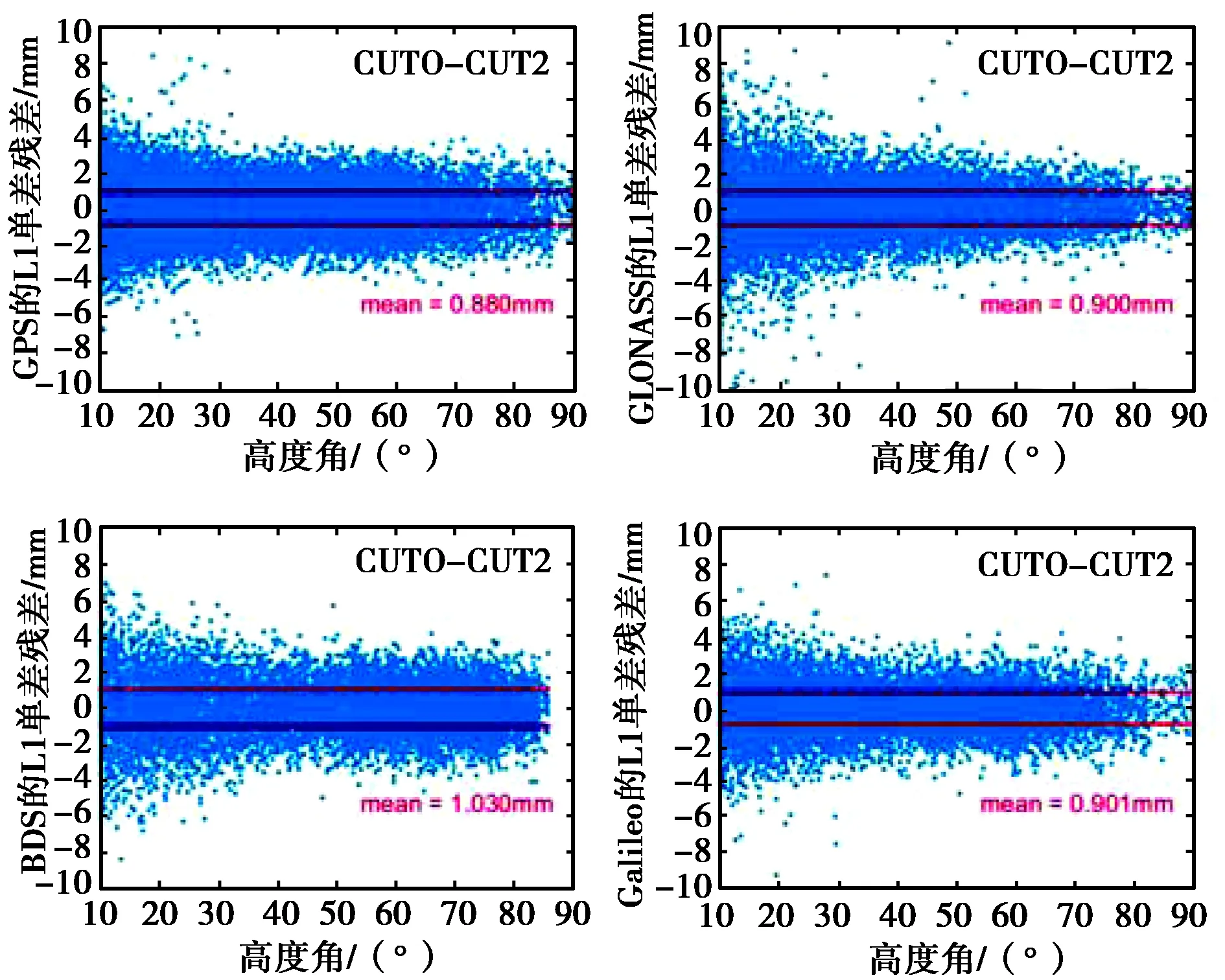
图3 各卫星系统L1载波相位单差残差与高度角关系图

图4 各卫星系统L2载波相位单差残差与高度角关系

2.3 四系统观测值质量与高度角相关性分析

卫星高度角是评价观测值质量的重要指标之一,基于高度角定权可进一步提高定位解算精度[5-10]．本文采用高度角定权中的正弦函数模型和指数函数模型进行观测值质量评估,其扩展形式如下:

(11)

式中：a、b和c0、c1、E0为常数项；Ele为高度角.戴[10]和Han[11]给出GPS系统高度角模型经验值如表1所示.

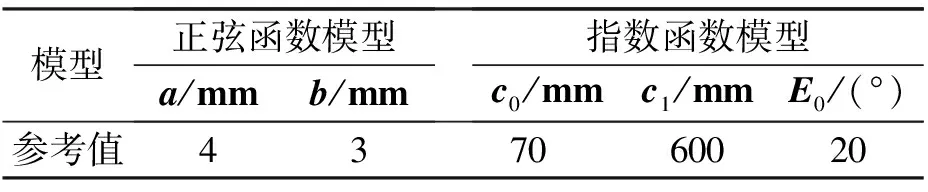
表1 文献中正弦模型和指数模型的经验值

本文对每颗卫星以1°高度角为间隔逐次估计RMS均值,记录该值随高度角的变化情况,并基于此序列对正弦模型和指数模型参数进行拟合,从而获得适用于不同系统不同频率载波观测值的随机模型．图5、图6示出了各卫星系统L1、L2载波相位观测值精度随高度角变化情况及相应的正弦模型和指数模型拟合曲线,两模型的拟合参数估值如表2所示．

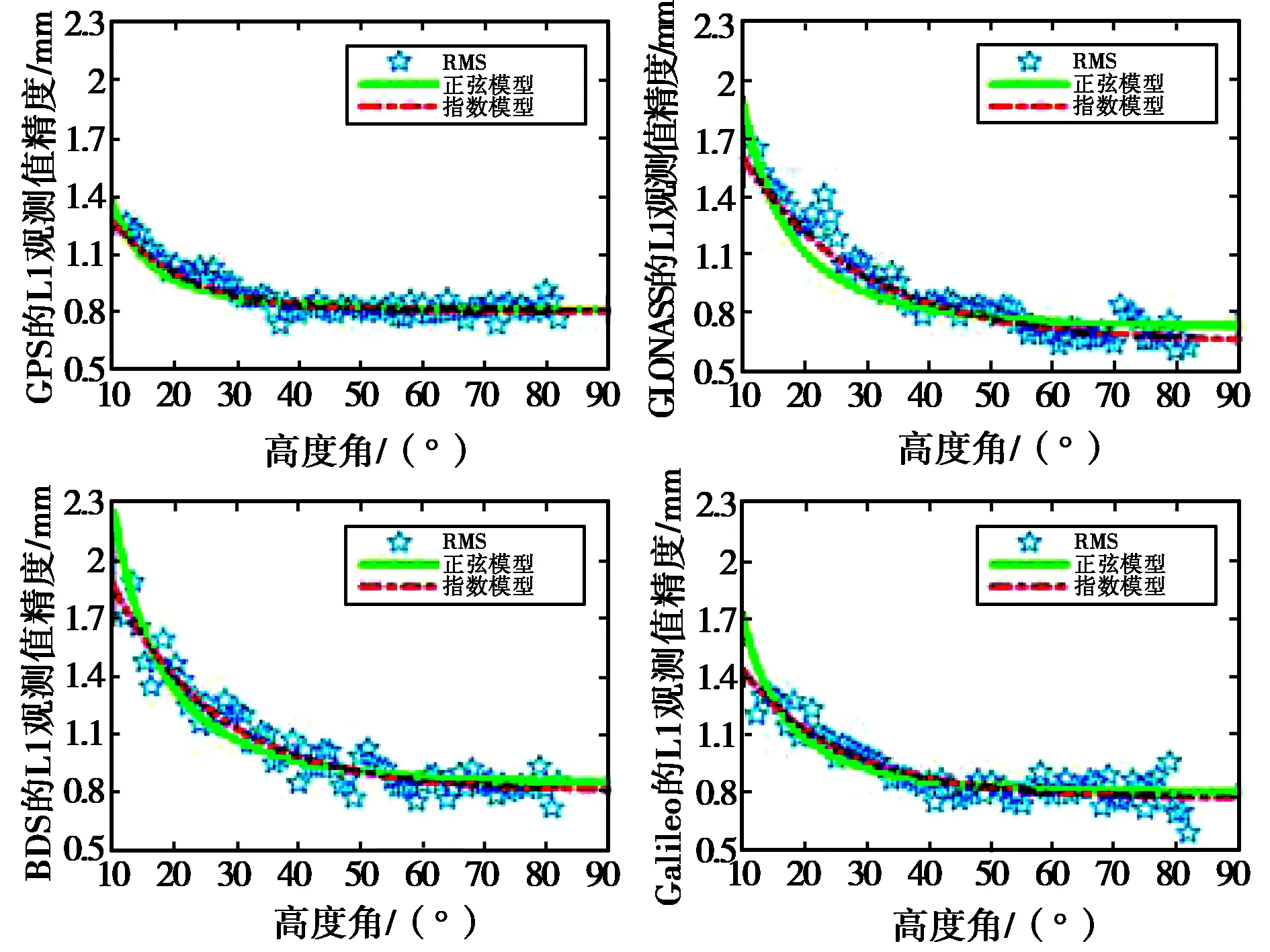
图5 各卫星系统L1观测值质量随高度角变化

图6 各卫星系统L2观测值质量随高度角变化

卫星系统L1正弦函数模型a/mmb/mmL1指数函数模型c0/mmc1/mmE0/°L2正弦函数模型a/mmb/mmL2指数函数模型 c0/mmc1/mmE0/(°) GPS1.10.31.11.911.41.10.71.47.010.6 GLO0.90.50.92.519.01.60.80.63.552.4 BDS1.10.51.12.717.01.10.81.13.623.2 Gal1.10.41.11.716.21.00.41.12.614.4

由图5可知,各系统各频率的相位观测值精度均与高度角相关且表现不同性质．GPS、Galileo系统正弦模型和指数模型在L1和L2上拟合曲线均与系统原始观测值精度相一致,并且两拟合曲线相关性极高;高度角高于40°后,非差观测值精度均趋近于一个常数．对于BDS系统,L2观测值精度统计信息与两个函数模型匹配度较高,但L1拟合效果相对略差,与观测值本身RMS值之间差异较大有关;高度角为10°时,L2频率上正弦函数拟合值与RMS计算值相差将近1mm,表明该模型在低高度角范围拟合效果比指数模型差．GLONASS系统L1频率的观测值精度极大地优于L2精度,且两个函数模型拟合曲线与实际值更为符合,正弦模型比指数模型拟合效果稍差;L2观测值精度与L2单差残差随高度角变化情况一致,随着高度角增大并未趋于稳定,相邻高度角之间RMS值的差异也较大,指数模型在15°～55°范围内与RMS序列较为符合,而正弦函数模型整体拟合效果不能准确反应该系统L2观测值统计特性．当高度角大于70°,Galileo、GLONASS等系统观测值精度序列均存在发散现象,主要原因为当高度角太大时,观测数据较少而导致统计结果不准确．

表2中GPS系统两模型拟合参数值与表1相比,相差较大,可能是由于卫星信号自身质量、测站地理位置以及硬件配置等一系列原因的综合作用造成,进一步证明对不同系统不同频率载波相位观测值应根据实际应用的具体情况而选择不同的高度角函数模型[5]．

3 结束语

本文基于几何无关和M-W组合方法,通过零基线实验计算了各系统单差残差序列并分析其随高度角变化情况,统计载波相位观测值精度与高度角相关性并对高度角加权模型中的正弦模型和指数模型进行精化,获得了适应于不同系统不同频率观测值的随机模型．各系统各频率观测值单差残差序列均随高度角增大而收敛,但不同系统不同频率其相关性不同．Galileo系统观测值在L1、L2频率上的整体精度最高,均在0.9mm左右;其他系统则表现出L2精度比L1精度更差的性质,尤其GLONASS系统L2观测值精度大于1.5mm,还需进一步提升以便更好地为GNSS各应用领域提供服务．正弦模型和指数模型对GPS和Galileo系统的L1、L2精度序列拟合一致性较好,而BDS系统使用正弦模型拟合效果略差,GLONASS系统则不适合采用正弦模型评估L2观测值精度．因此,对不同系统不同频率载波相位观测值应根据实际应用的具体情况来选择不同的高度角模型．