顾及MLE的IGS坐标时间序列噪声模型特性分析

王子舆,李仲勤

(兰州交通大学 测绘与地理信息学院,甘肃 兰州 730700)

0 引 言

国际全球卫星导航系统(GNSS)服务组织(IGS)坐标时间序列中包含相关有色噪声的结论已经得到了广泛的认可．不同噪声模型对GPS站速度及其不确定度影响较大,如闪烁噪声(FN)、白噪声(WN)、随机游走噪声(RW)和幂律噪声(PL)．随着对GPS坐标时间序列噪声特性的研究,有学者认为纯WN的假设会导致速度不确定度过低估计[3],也有学者认为WN+FN模型是GPS噪声模型中的最优模型,文献[1]得出结论如果忽略相关噪声的影响,其速度不确定度将被过低估计达一个数量级,但文献[4]研究表明WN+FN噪声模型代替WN模型时测站速度不确定度将增大3～6倍;文献[5]中提出,PL模型、高斯-马尔科夫模型(GGM)等可用于分析GPS时间序列,文献[6]中研究发现GPS坐标时间序列中包含有一阶高斯-马尔科夫噪声和带通滤波噪声,并在美国南加州等地检测到此类噪声．综上研究分析,学者研究存在差异的原因可能如下:1)选取的噪声模型过于单一;2)选取的不同区域的GPS坐标时间序列存在差异;3)选取的GPS坐标时间序列长度较短．GPS站坐标的时间序列及噪声特征有助于获取模型参数估计的实际不确定度,正确分类及改正噪声分量对于合理应用GPS坐标时间序列数据具有重要的意义．

为此,本文以全球范围内30个GPS站10年的坐标时间序列为研究对象,采用赤池信息量准则 (AIC)及贝叶斯信息准则 (BIC),分析对比FN+RW、FN+WN、FN+WN+RW、PL及WN五种组合噪声模型,并探讨改进的最大似然估计 (MLE)噪声模型估计及其噪声模型对GPS站速度及其不确定度的影响．

1 噪声模型评价准则

传统的MLE方法在噪声模型估计方面存在不足．随着噪声模型包含的未知参数越多,估计出的MLE值越大[6]．为此,需要更为准确的噪声模型估计准则判定GPS时间序列噪声模型估计的可靠性．

1.1 AIC噪声模型估计准则

研究分析较长周期的GPS坐标时间序列及噪声特征需选择合适的噪声模型估计准则,而噪声模型估计准则直接影响最优噪声模型的选取．本文采用改进的AIC,其原理[7-8]为

AIC=-2lnL+2k.

(1)

式中:L为某一模型中的似然函数;k为模型变量个数,判定最优模型时,AIC最小的模型作为最优模型．

1.2 BIC噪声模型估计准则

相比AIC,增加了参数数量,即模型复杂度,会增大似然函数,但是也会导致过拟合现象,BIC原理[9]为

BIC=kln(n)-2ln(L),

(2)

式中:n为样本数量,其余变量的意义见式(1),BIC越小,对应的模型越接近最优模型．

2 噪声模型对IGS站速度及其不确定度影响分析

2.1 GPS站速度模型的建立

目前国内外许多学者探讨分析噪声模型对IGS站速度及其不确定度的影响,KLOS、BOS等人[8,10]假设GPS站速度用线性回归法拟合估计,噪声模型对站速度的准确估计可表示为

mv≈±

(3)

式中:N为观测值时间序列长度;κ代表估计谱指数;ΔT为采样率;APL为噪声振幅;τ为伽玛函数．

2.2 GPS时间序列噪声模型分析

以30个GPS站7～10年的坐标时间序列为研究对象,采用AIC模型估计准则及BIC噪声模型估计准则,分析对比FN+RW、FN+WN、FN+WN+RW、PL及WN五种组合噪声模型对GPS站速度及其不确定度的影响分析．表1示出了AIC方法估计出的不同噪声模型在E方向、N方向及U方向的最小值个数及所占比例如表1所示．

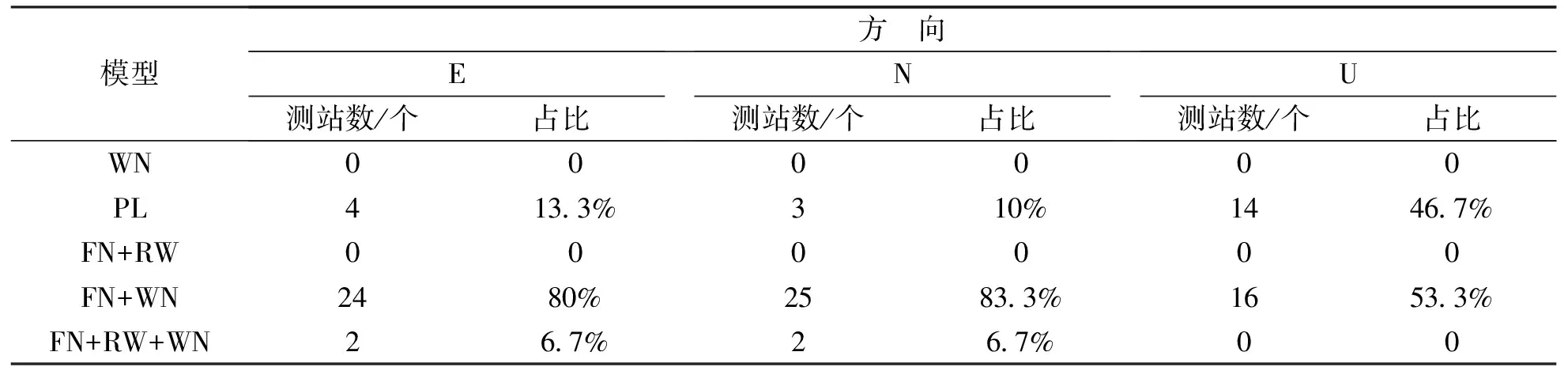
表1 不同模型下AIC最小值分布结果

由表1可得,坐标E方向主要表现为FN+WN模型(约80%)、PL模型(约13.3%)以及FN+RW+WN模型(约6.7%);坐标N方向主要表现为FN+WN模型(约83.3%)、PL模型(约10%)、部分表现为FN+RW+WN模型(约6.7%);坐标U方向分量主要表现为FN+WN模型(约53.3%)和PL(约43.3%)模型．

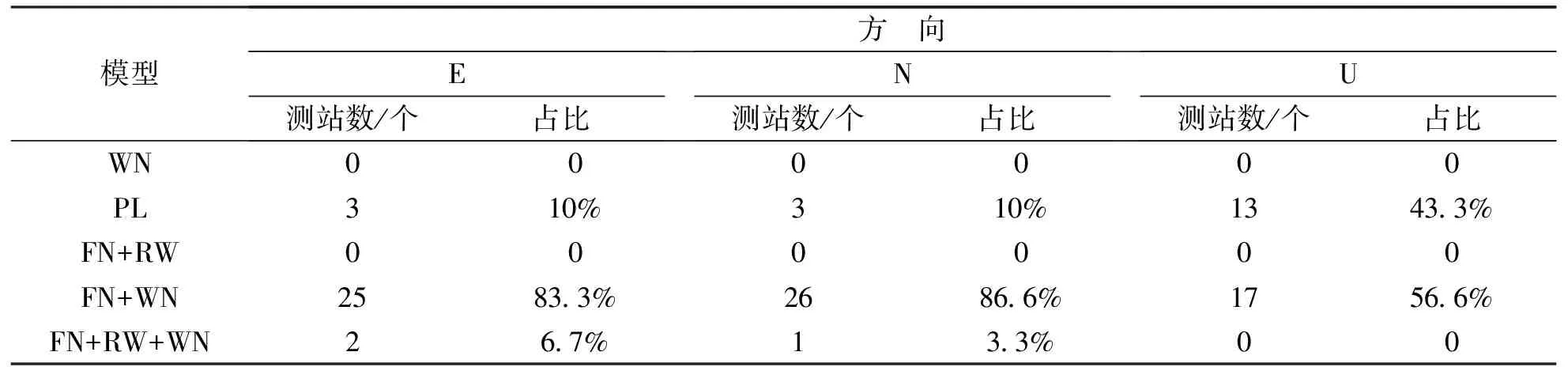
表2 不同模型下BIC最小值分布结果

从表2可得,坐标E方向主要表现为FN+WN模型(约83.3%)、PL模型(约10%)以及FN+RW+WN模型(约6.7%);坐标N方向主要表现为FN+WN模型(约86.6%)、PL模型(约10%)、部分表现为FN+RW+WN模型(约3.3%);坐标U方向分量主要表现为FN+WN模型(约56.6%)和PL(约43.3%)模型．由表1表2可知:1)AIC与BIC噪声模型估计准则对最优噪声模型的判定可靠性高,每个方向(E、N、U)仅存在一个站点的差异(如AIC,FN+WN测站数为24个,BIC,FN+WN测站数为25个);2)GPS站坐标时间序列噪声模型主要表现为FN+WN模型、PL模型以及FN+RW+WN模型,说明GPS时间序列噪声模型具有多样性,传统的WN和FN的最优噪声模型模型不具有普遍性和最优性;3)少数测站呈现出FN+RW+WN模型,其中RW模型特性主要分布在水平方向上,说明测站水平方向引起的RW分量不可忽略,如呈现出FN+WN+RW模型特性的PIMO站,站点位于菲律宾,因受到2011年日本大地震的影响,导致测站向E、N方向同震位移60 mm,说明受同震、震后变形影响,是GPS站噪声模型特性呈现出RW特性的原因之一．

2.3 噪声模型对IGS站速度的影响分析

为了探讨噪声模型对GPS站速度的影响,本文以FN+RW+WN、WN、PL、FN+WN、FN+RW五种噪声模型为例, 以FN+WN+RW为基准模型,与其他四种噪声模型站速度求差, 分别对测站E、N、U三组坐标分量的速度差值对比分析,得出不同噪声模型背景下速度差值估计结果,如图1所示．

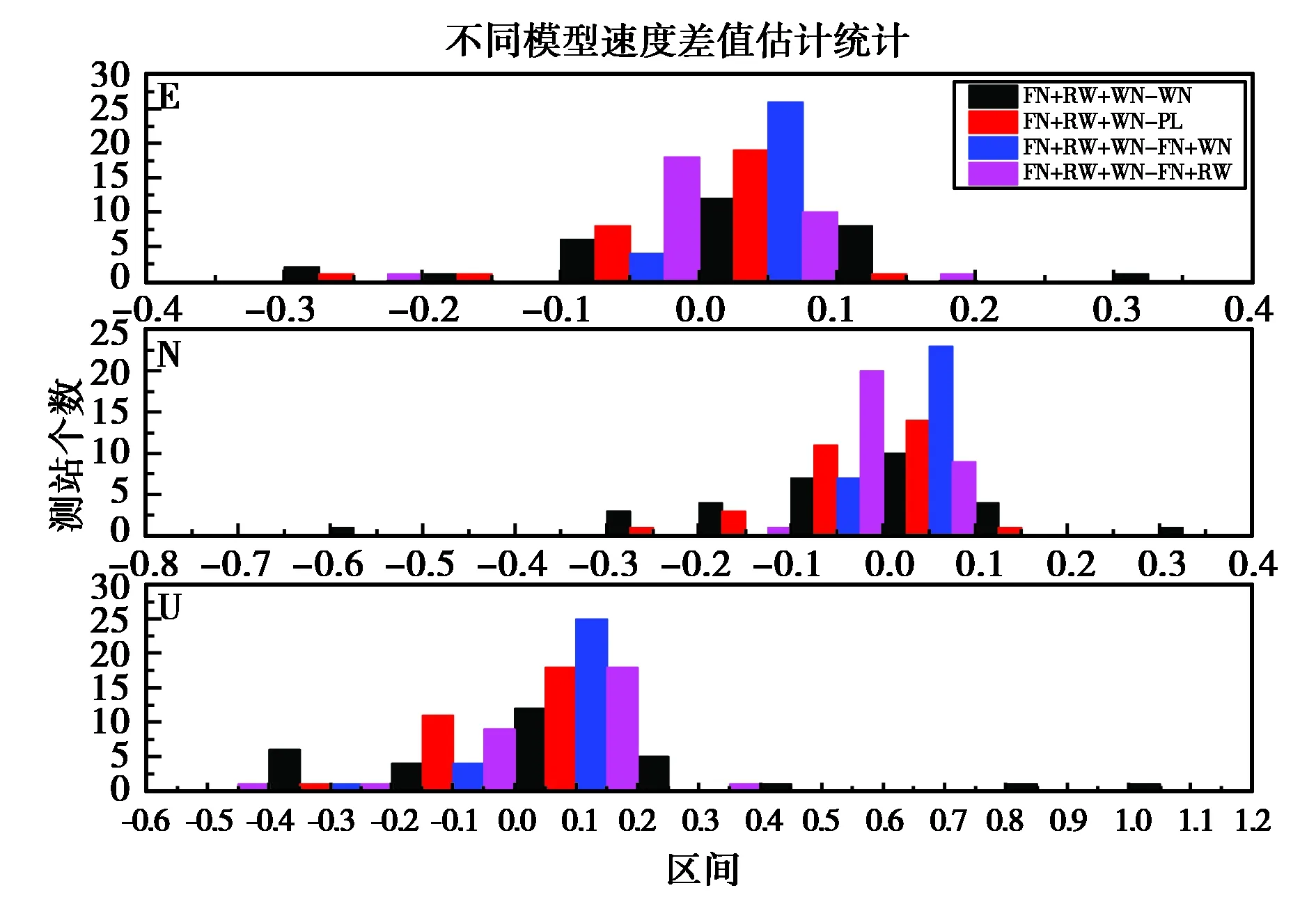
图1 E、N、U三方向不同噪声模型站速度差值估计分布

由图1可知,E方向不同噪声模型站速度差值较小,集中分布在0～0.1 mm/a,FN+RW+WN与FN+WN站速度差值较为集中,约83.3%以上站速度差值小于0.1 mm/a;N方向上站速度差值介于-0.1～0.1 mm/a,最大值约为0.3 mm/a;U方向站速度差值较E方向与N方向的站速度差值较大,站速度差值介于-0.4～0.2 mm/a,个别测站最大站速度差值达到1.0 mm/a.进一步对GPS站速度估计值进行统计分析,不同噪声模型站速度差值极值表如表3所示．

表3 不同噪声模型速度差值极值

由表3可知,E方向不同噪声模型站速度差值均值小于0.03 mm/a,最小值为0.052 mm/a,最大值为0.368 mm/a;N方向不同噪声模型站速度差值均值与E方向一致均小于0.03 mm/a,速度差值最小值为0.002 mm/a,最大值为0.504 mm/a;U方向站速度均值相比E、N方向略大,均值小于0.09 mm/a,最小值为0.03 mm/a,最大值为1.045 mm/a．综上可知在E、N方向上,FN+WN+RW与WN、PL、FN+RW、FN+WN的站速度差值较小,但在U方向上,不同噪声模型站速度差值略大于E、N方向的站速度估计差值,说明不同噪声模型对站速度的影响在U方向表现更为明显．

2.4 噪声模型对IGS站速度不确定度的影响分析

已有研究结果表明噪声模型对速度不确定度的影响较大,为了深入分析噪声模型对IGS站速度不确定度的影响,以FN+WN+RW为参照,对所选的30个IGS站在不同噪声模型下的速度不确定度进行分析,图2示出了E、N、U方向不同模型下速度不确定度差值比较结果，如图2所示．

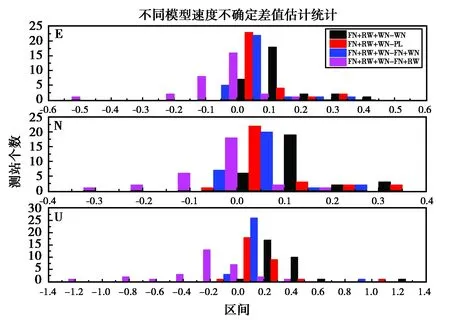
图2 E、N、U三方向不同噪声模型站速度不确定度差值估计分布

由图2可知,E方向不同噪声模型站速度不确定差值较小,集中分布在0～0.05 mm/a, FN+RW+WN与FN+WN及FN+RW+WN与FN+RW的站速度差值小于0.1 mm/a的约占93.33%;N方向上不同噪声模型站速度变化与E方向相近,但U方向上,不同噪声模型站速度不确定度差值变化较大,其差值分布于-1.2～1.3 mm/a区间,经offset资料查证,个别测站如GOUG与PIMO测站受offset影响,其中GOUG站E、N、U方向RW占比分别为2.8%、1.8%、0%,对应的RW分量振幅分别为5.3、4.4、0.0 mm/a r0.5,而BRMU站E、N、U方向RW占比分别为1.5%、0.0%、1.4%,对应的RW分量振幅分别为4.1、0.0、10.5 mm/a r0.5．综上表明,U方向上,RW分量对站速度不确定度有一定的影响,且影响不可消除．

为了较深入地分析噪声模型对测站速度不确定的影响结果,以FN+WN+RW为参照,对所选的30个IGS站在不同噪声模型下的速度不确定度比值分析,如图3所示．

由图3可知,FN+RW+WN噪声模型与WN噪声模型站速度不确定度比值,在E、N、U方向三坐标分量比值最大,分别约为5.3～21.5倍、5.8～21.4倍、5.2～20.3倍; FN+RW+WN噪声模型与FN+WN噪声模型站速度不确定度比值,在E、N、U方向,三坐标分量为1.0～3.1倍、1.0～3.2倍、1.0～2.5倍．综上表明:1)假定的GPS坐标序列为白噪声模型时,对测站速度不确定度过高估计;2)不同噪声模型对E、N、U方向上的速度不确定度不可忽略,尤其为U方向．

3 结束语

本文选取30个GPS站坐标时间序列,探讨AIC与BIC噪声模型估计准则对最优噪声模型选取的可靠性,以FN+WN+RW噪声模型为参考,与WN、PL、FN+WN、FN+RW噪声模型对比分析,分析噪声模型对GPS站速度及其不确定度估计的影响．得出以下结论:

1)AIC与BIC噪声模型估计结果可靠性高,GPS时间序列主要表现为FN+WN模型、PL模型以及FN+RW+WN模型,说明GPS时间序列噪声模型具有多样性,传统的WN和FN的最优噪声模型不具有普遍性和最优性,此外,当AIC与BIC噪声模型估计结果不一致时,需进一步研究．

2)不同噪声模型对GPS站速度及其不确定度影响较小,但不同噪声模型E、N、U方向不确定度估值差异较大,且在U分量更为明显．

3)特殊地理位置的GPS测站(如处于地震带的测站),存在RW噪声模型特性,但占比较小,说明地震是引起RW噪声特性的因素之一．对GPS时间序列进行噪声模型估计时,可将地震带的测站做标记研究,尽量减少RW带来的不利影响．