基于混沌序列的SCMA码本设计及系统性能分析

赵耿，马艳艳，马英杰

（1. 西安电子科技大学通信工程学院，陕西 西安 710071；2. 北京电子科技学院网络空间安全系，北京 100070）

1 引言

随着科技的不断发展和网络的大规模商业化，5G技术的研发已成为移动无线网络发展的重要推动力。未来海量设备的连接和种类繁多的物联网业务给无线接入技术带来了巨大的挑战[1]，对网络效率和系统容量提出了新的需求。高容量和高效率的新型多址技术成为了学科和社会各界关注的热点，其中稀疏码多址接入（SCMA, sparse code multiple access）技术脱颖而出，成为5G多址接入候选技术之一[2-3]。SCMA技术是一种热门的非正交多址接入方式。在SCMA编码系统中，不需要原始分多址中的调制和扩频，每个用户都有属于自己的码本（CB，codebook）[4]，编码比特流直接映射到SCMA码本的一个多维码字上，且多个用户的码字在资源块上叠加传输，可以成倍增加用户数量，从而更好地提升系统整体容量。近些年，国内外学者都在不断规范码本设计的通用原则，主要是以低密度签名（LDS,low density signature）为基础的优化改进算法[5]。目前，对SCMA系统的研究大多以码本设计方法为重点，主要分为两大类：一类是基于格的星座设计原则[6]，比较常用的方法是多维格型星座的设计方法，该方法利用独立QAM（quadrature amplitude modulation）星座的笛卡尔积来建立多维星座，从而设计码本[7]；另一类是以旋转为设计原则，比如基于星型QAM信号星座图的SCMA系统，就是采用旋转相位的方法设计码本[8]。此外，利用信号空间分级技术解决多维星座设计问题也是一个研究热点，通过代数数论或计算机搜索构造酉矩阵旋转 QAM星座图，从而建立多用户码本[9]。

上面提到的设计方法都是通过改变码本的设计规则来提升SCMA的系统性能，虽然已经达到良好的效果，但是系统始终采用传统随机序列选择码本。面对未来5G海量用户的信息传递需求，系统的安全性必须有更好的保障。本文通过对SCMA系统的研究和对混沌序列的理解，打破常规，首次提出不改变码本设计方法，仍采用基于网格编码调制（TCM，trellis coded modulation）的子集分割法设计星座图[10]，将混沌序列代替随机序列应用到SCMA系统中，改变用户选择码本的方式，并通过实验仿真证明了这一方法在不改变编码效率的条件下进一步降低了系统的误码率。

2 基于混沌序列的SCMA系统分析

2.1 logistic混沌序列的动力学特性

混沌现象从确定非线性系统的演化过程来看是指内在的随机性，它们在混沌区的行为都表现出随机不确定性，然而这种不确定性不是来源于外部环境的随机因素，而是系统自发产生的[11]。用于 SCMA系统的混沌序列通常通过映射模型产生，其中 logistic混沌映射是一个被广泛研究的非线性系统[12]，由于其形式简单且具有复杂的动力学行为，是一个由倍分期分叉到达混沌状态的典型例子。该映射的方程为

其中，1≤μ≤ 4，μ被称为分形参数，logistic混沌映射的动力学行为与μ密切相关。当 3.566≤μ＜ 4时，系统处于混沌状态，产生的混沌序列具备非周期性且对初始状态极其敏感；当μ=4时，称为logistic满混沌映射，此时映射的输出信号如图1所示，相轨迹如图2所示。

由图1和图2可知，此时输入区间与输出区间的分布都在（0,1）区间，且图1的输出的序列值呈随机分布。满混沌映射的概率密度函数如式（2）所示。

图1 logistic满混沌映射输出信号

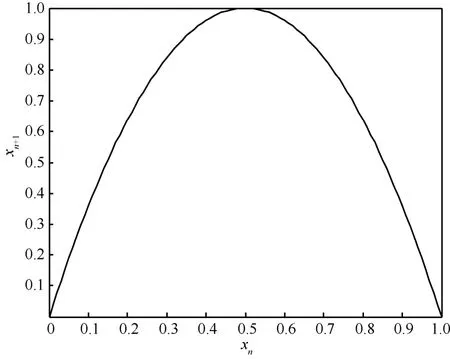
图2 logistic满混沌相轨迹

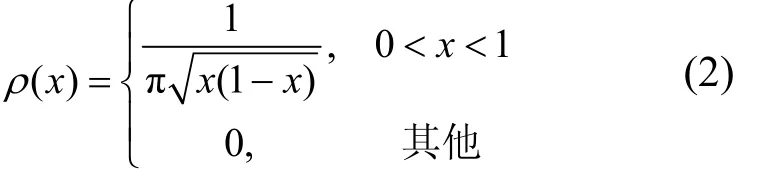
由式（2）计算得到序列的均值如式（3）所示，自相关函数如式（4）所示。

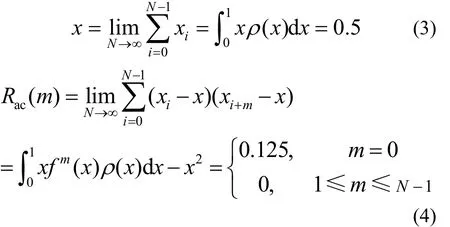
其中，m表示序列间隔。

给出2个不同的初始值x10和x20，迭代产生2条不同的序列，它们的互相关函数如式（5）所示，可见序列几乎互不相关。

其中，fm（x）=f（f…f（x）…）。

由式（3）可知序列的平均值为 0.5，因此二值量化的判决门限可以选为0.5，量化方法如式（6）所示。对量化后的logistic混沌序列进行相关性能的仿真，其自相关性如图3所示，互相关性如图4所示。

图3 二值量化后序列自相关性

图4 二值量化后序列互相关性

由图3和图4可知，二值量化后logistic混沌序列的自相关函数值和互相关函数值都非常小，基本稳定在0.2～0.3，相关性能良好。

2.2 SCMA编码原理

假设6个用户在4个资源块上传输信息，采用四点星座图调制，由SCMA基本原理可知，用户将被分配到属于自己的码本，是一个4×4的复数矩阵，矩阵的行代表资源块，列代表码本的码字。设每个用户每次传输的比特数为b，则需要占用的星座数为

即分别对应2b个码字。用户将数据流通过信道编码映射到预定义码本的码字上，在这里假设每个用户传输2 bit信息，所以有4种可能，用（0,0）、（0,1）、（1,0）、（1,1）表示，对应4个码字，分别是码本的第1～4列，如图5所示。

图5 SCMA编码原理

6个用户同时发送消息，假设用户1传输（1,1），用户 2 传输（1,0），用户 3传输（0,0），用户4 传输（0,1），用户5传输（1, 0），用户6传输（0, 0），各用户分别对应各自码本的第4、3、1、2、3、1列码字。6个用户的码字叠加后在4个资源块上进行传输，白色的块表示用户不占用该资源块。在SCMA系统中，为了表示方便，引出映射矩阵F的概念，矩阵中元素1的位置表示该资源块上有信号进行传输，0表示没有信号，一般通过手动设计得到。故图5对应的映射矩阵F为

每个用户仅利用 2个资源块，例如用户 1只在资源块 1和资源块 2上进行传输。而每个资源块只有 3个有效用户，例如第 1资源块只有用户 1、3、5使用。因此，在使用相同频谱的情况下，SCMA通过多址码域的引入，大大提升了频谱效率。

3 基于logistic混沌序列的SCMA系统设计

3.1 系统设计方案

SCMA是以扩频码分多址（CDMA, code division multiple access）为基础发展而来的一种多址接入方式[13]。它将 QAM 映射器与 CDMA扩频器结合起来，通过星座调制和映射矩阵扩频生成码本。各用户的输入信号由 SCMA编码器编码后，由 logistic混沌序列选择出对应码本的码字，叠加后经高斯信道到达解码端。由于SCMA系统具有稀疏特性的优点，采用复杂度较低的MPA（message passing algorithm）算法在解码端进行解码，可以实现近似用户最大似然解码[14]，系统方案如图6所示。

图6 系统方案

SCMA编码器是将二进制比特流映射为一个N维码字的过程。用户通过SCMA编码器将输入的信号（二进制数据比特流）分别映射到多维码本的码字上，用户k的SCMA编码器可表示为

其中，b为用户k输入的比特流，fk为用户比特流到码本的映射关系函数，xk为用户k对应的N维码本。

在多用户传输时，每个用户都对应属于自己码本的码字，经 logistic混沌序列选择后叠加，通过高斯信道传输至系统的接收端，接收到的用户层的叠加信号为

其中，xj是用户j的N维码字，hj是用户j的信道向量，n是均值为0、方差为σ2的高斯白噪声。

3.2 SCMA码本的设计

SCMA采用设计好的多维码本替代QAM调制器和稀疏序列扩频器，使系统具有多维星座的赋形増益[15]，通过码本的多维星座能提高频谱效率，并实现过载，此外，还可保持较低的译码复杂度。

3.2.1 设计资源块上的星座图

SCMA系统中一个资源块上重载的用户越少，系统产生的碰撞越少，越能降低误码率。但是一旦用户数变多，尤其面对未来海量用户的接入，同一个资源上互相影响的用户数量必然增加。用户的码字是由信息比特流通过多维星座映射得到的，因此要求用户对应的星座点在同一个资源块上不能重合，那么设计有效的多维星座是系统设计的关键点之一。

本文采用基于TCM子集分割法的星座图设计方法[10,16]，使用现有的调制星座图，如PSK（phase shift keying）星座，采用TCM子集分割法产生各用户对应的有效星座集合。由式（7）可知，若每个用户每次传输的比特数为b，则需要占用的星座点数为B个，假设每个资源块上有M个有效用户，则每个资源块上总的星座点数为

于是采用Bs点PSK星座，然后进行TCM子集分割，得到M个子集，分别对应资源块上M个有效用户。

3.2.2 构造映射矩阵

映射矩阵F可以反映出每个资源块上的用户数以及资源块的利用情况。假设SCMA系统的子载波数为N，即码字的长度，K表示非零元素数，那么SCMA系统的最大用户数为

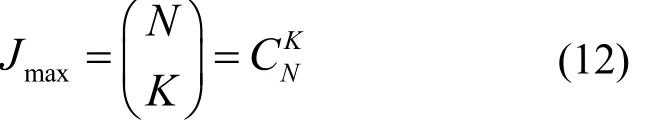
每个资源块上传输的实际用户数为

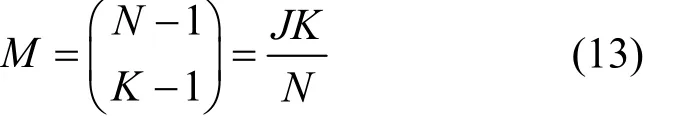
过载率为

实际用户数也影响了 MPA检测的复杂度，编码后的码字拥有的非零项越少，MPA检测的复杂度越低。由于映射矩阵与低密度奇偶校验码（LDPC,low density parity check code）的校验矩阵具有相似性[17]，只需知道系统的资源块数、用户数、行重（每个资源块上的有效用户）、列重（每个用户利用资源块数），就可以通过设计规则的 LDPC校验矩阵来得到具有较好性质的映射矩阵，也可以手动设计。

3.2.3 生成码本

将星座图与映射矩阵结合起来生成星座矩阵。星座矩阵中星座的位置对应映射矩阵中元素 1的位置，且每个资源块上的有效星座子集位置是随机的，只需保证选择的星座子集是不重复的。然后将每一列展开为n×m矩阵，n为矩阵第一维，表示资源块数；m是第二维，表示码字；第三维是用户。n×m矩阵即为每个用户的码本。

4 SCMA码本设计仿真研究

6个用户在4个资源块上传输，每个用户仅占用2个资源块，且每个资源块上实际有效用户只有3个。由式（7）可得，每个用户每次传输的比特数为2 bit，则需要占用的星座点数为4。由式（11）可得，每个资源块上的总星座数为4×3=12个，采用12点PSK星座进行子集分割，得到3个子集，分别对应资源块上3个有效用户，如图7所示。

图7 12点PSK星座分割子集

图7中，圆点星座用A1表示，三角星座用A2表示，方形星座用 A3表示，根据要求手动设计F矩阵如式（15）所示。

结合图 7和式（15）可以得到用户与资源块的星座矩阵图。每个资源块上实际的有效用户只有3个，且这3个用户选择子集星座是随机的，但是3个子集组合起来正是12点PSK星座图。因此，用户与子集星座之间有多种对应关系，随机选择一种如图8所示。

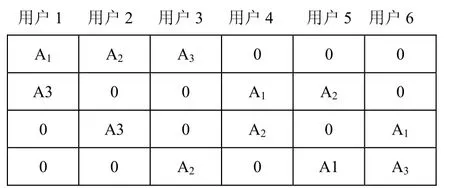
图8 星座矩阵

假设第1个码字到第4个码字分别对应星座图上的第一象限到第四象限的值，由图8可知，用户1的第一列码字的4个元素分别为A1的第一象限值、A3的第一象限值、0、0；第二列码字的4个元素分别为A1的第二象限值、A3的第二象限值、0、0。以此类比可以得到 6个用户的TCM码本如下。

用户1

用户2

用户3

用户4

用户5

用户6

4.1 不同信号下性能分析

在高斯白噪声下，系统采用 logistic混沌序列选择用户对应码本中的码字，与文献[10]中使用传统随机序列选择码字进行对比，并进一步使用文献[11]中改进的 logistic混沌序列代替系统的logistic混沌序列进行对比。采用码率Turbo编码，在MPA算法译码下，迭代8次，用户传输1 000 bit信息，得到的误码率（BER, bit error rate）对比仿真曲线如图9所示。其中，横坐标为信噪比（SNR,signal noise ratio）。

由图 9可以看出，采用 logistic混沌序列选择SCMA系统的码字时，在不改变编码效率的条件下误码率低于传统随机序列。当信噪比达到10 dB时，系统误码率出现小幅度降低，并且随着信噪比的增大，降低幅度不断增大，当信噪比等于14 dB时，误码率明显降低。若使用改进的logistic混沌序列选择码本时，系统的误码率又有了非常明显的降低，特别是当信噪比达到14 dB时，系统的误码率骤降。这一方面说明logistic混沌序列的随机性和非相关性虽然很强，但是仍可以进一步改进；另一方面，SCMA系统充分利用了星座的赋形增益，有效降低了接收端解码复杂度，消除了用户之间的干扰。

图9 采用不同序列误码率对比

4.2 不同过载条件下性能分析

系统采用 logistic混沌序列来选择用户对应码本的码字。假设有6个资源块，每个用户实际利用的资源块为2块，那么最大用户数为15。分别取用户数为6、9、12这3种情况，则对应的过载率为100%、150%、200%，以上3种情况仍采用码率Turbo编码和MPA算法译码，迭代8次，得到的BER-SNR性能仿真曲线如图10所示。

图10 不同过载率条件下误码率对比

由图 10的仿真结果可得以下结论。当用户数一定时，系统误码率随着信噪比的增加而显著减小。当信噪比相同时，系统未达到过载，即λ=1，系统的误码率较低；达到过载后，随着过载率的增大，用户干扰增加，系统的误码率明显增大。信噪比越大，过载率对系统误码率的影响也越大。这是因为过载能力越大，接入用户越多，用户之间干扰增大，彼此间竞争也增大，并且解码也变得比较困难。因此，合理选择过载率，对提高系统的误码率性能至关重要。

5 结束语

在SCMA系统传输过程中，设计出好的码本可以在不增加频带利用率、不改变编码效率的前提下有效降低误码率，提高系统的容量和效率。面对未来5G海量用户的需求，不仅需要好的码本，高效性和安全性也是需要重视的问题。本文设计使用logistic混沌序列来选择用户对应码本的码字进行用户信息传输。仿真结果表明，与使用传统随机信号相比，本文系统传输的误码率明显降低，且改进型的 logistic混沌序列效果更优。这不仅说明了SCMA系统具有安全性和高效性，更有力证明了混沌序列的伪随机特性。并且在不同过载率的条件下，系统的性能依然良好。