非高斯噪声与高斯色噪声作用的基因调控网络研究

马相毓，仝卫明

(1.山西大学 数学科学学院，太原 030006；2.太原科技大学 应用科学学院，太原 030024)

基因调控在生命活动中具有非常重要的作用。随着科学技术的不断进步，越来越多的研究表明基因调控是一个非线性随机过程[1]。噪声的扰动对非线性系统有很大的影响，许多学者研究[2]指出噪声可诱导基因突变，导致癌症的发生，因此研究噪声作用下的基因调控十分必要。BALTAZAR et al[3]于2008年提出了一个抽象模型，该模型耦合了E2F/Myc正反馈过程和E2F/Myc/miR-17-92负反馈过程，结果显示不同浓度的转录蛋白因子E2F和Myc在细胞的增值与凋亡过程中扮演着不同的角色。对于该模型，LI et al[4]研究发现miRNAs能导致系统出现双稳现象，并且可以优化基因的“开-关”过程；同时研究表明正反馈过程会导致噪声的敏感性，负反馈过程对噪声有抑制作用。ZHANG et al[5]发现减少噪声的自相关时间会加强对噪声的抑制，但不影响系统的敏感性。

目前，许多研究是关于高斯白噪声对基因调控过程的影响，高斯白噪声是一种理想噪声，而实际生活中的噪声主要是非高斯噪声或高斯色噪声。因此，研究非高斯噪声与高斯色噪声激励下的基因调控是非常有意义的。本文将非高斯噪声和高斯色噪声作用到BALTAZAR et al[3,6]建立的基因调控模型中，通过求解与系统对应的FPK方程，得到系统的稳态概率密度函数。研究了非高斯噪声强度 、偏离高斯噪声程度以及两噪声的互相关强度对基因调控过程的影响。

1 基因调控过程的动力学模型

将非高斯噪声和高斯色噪声作用到BALTAZAR et al[3,6]建立的基因调控模型上，得到如下新模型：

(1)

式中：x表示蛋白质(Myc和E2F)的浓度；μ为胞外生长因子刺激下基本蛋白质表达效率；k表示蛋白质的自动催化效率；β1为蛋白质表达效率；β2为抑制蛋白质表达效率；η(t)和ξ(t)分别是非高斯噪声和高斯色噪声，且满足下列关系：

(2)

(3)

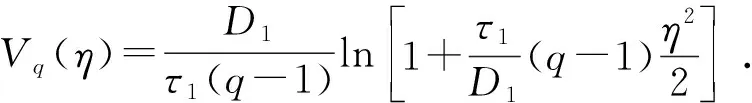
ε(t)和Γ(t)是高斯白噪声，其统计性质如下：

式中：D1,D2分别是非高斯噪声强度和高斯色噪声强度；λ为噪声间的相关强度；q为偏离高斯噪声程度；τ1为噪声相关时间。

根据文献[7-10]，可以得到η(t)的稳态概率分布

(4)

式中：Zq表示归一化常数(q<3)；η(t)的一阶矩和二阶矩分别为

〈η〉=0； 〈η2〉=2D1/τ1(5-3q);q<5/3 .

显然，当q=1时，η(t)为高斯色噪声。

进一步，当|q-1|=1，有[7-10]

(5)

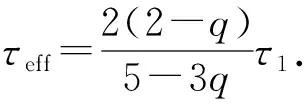
因此，方程(2)可以化简为：

(6)

其中，

方程(1)对应的势函数为：

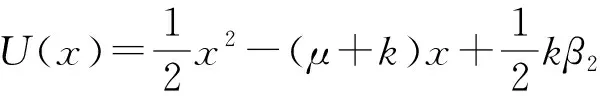
(7)

当μ=0.1，k=5.0，β1=1.0，β2=1.8时，系统的势函数如图1所示。从势函数图像可以看出方程(7)有一个不稳定解xu和两个稳定解x1，x2.通过计算得出xu≈1.040 4，x1≈0.126 1，x2≈2.133 5.

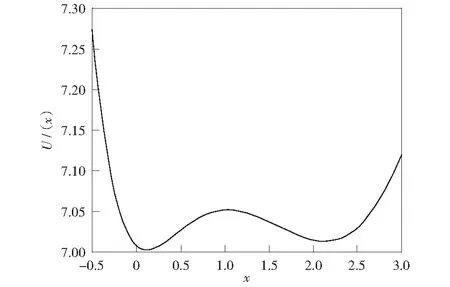
图1 模型(1)的势函数Fig.1 Potential function of system(1)

方程(1)对应的福克普朗克方程为[11-14]：

(8)

其中，

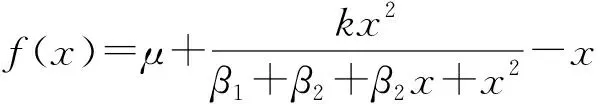
方程(8)的稳态概率密度函数分3种情况讨论，如下：

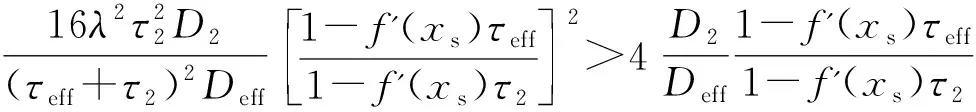
(9)

式中，N1为归一化常数，

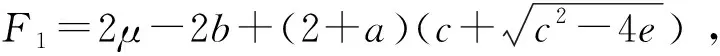
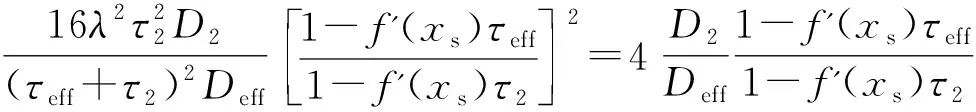
(10)

式中，N2为归一化常数，并且

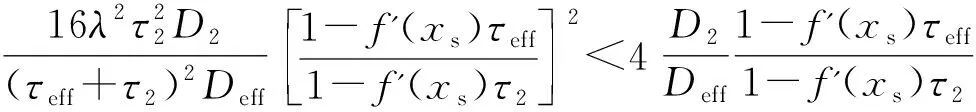
(11)

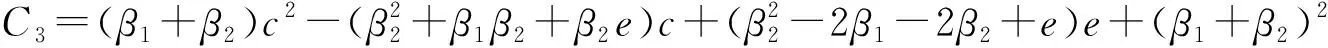
式中：

2 结果分析

根据上述方程(8)的解析解，用Matlab作出稳态概率密度Pst在不同参数下关于蛋白质浓度x的函数图像。图2表示其他参数相同、非高斯噪声强度D1不同的情况下，稳态概率密度函数Pst关于蛋白质浓度x的函数图像。图2表明：当非高斯噪声强度D1为0.1时，稳态概率密度主要分布在低浓度状态，此时基因处于“关”状态。随着D1逐渐减小，稳态概率密度在低浓度状态的峰值逐渐减小，同时在高浓度状态处出现峰值，并且峰值逐渐增加。基因从“关”状态向“开”状态转变。因此非高斯噪声的强度既可以影响基因转录的效率，又可以改变基因的“开-关”机制。

μ=0.1, k=5.0, β1=1.0, β2=1.8, λ=0.3, q=0.8, D2=0.03, τ1=τ2=0.3图2 不同非高斯噪声强度D1下概率密度函数Fig.2 Stationary probability distribution for different D1

图3表示其他参数相同、偏离高斯噪声程度q不同的情况下，稳态概率密度函数Pst关于蛋白质浓度x的函数图像。显然偏离高斯噪声程度q=1时，η(t)为高斯色噪声。从图3可以看出：当q从1.4逐渐减小到1，基因从“关”状态向“开”状态转变；当q从1逐渐减小到0.2，稳态概率密度主要集中在同一高浓度状态，并且峰值逐渐增加。说明此时基因的“开-关”机制不再改变，但转录效率逐渐提高。因此，当偏离高斯噪声程度q>1时，改变q的值不仅能影响基因转录的效率，还能改变基因的“开-关”机制。当偏离高斯噪声程度q<1时，改变q的值只能影响基因的转录效率，而不能改变基因的“开-关”转换机制。

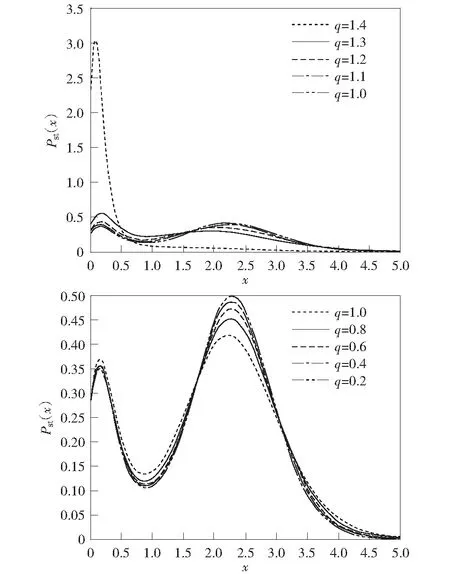
μ=0.1, k=5.0, β1=1.0, β2=1.8, λ=0.3, D1=D2=0.03, τ1=τ2=0.3图3 不同偏离高斯噪声程度q下概率密度函数Fig.3 Stationary probability distribution for different q

图4表示其他参数相同、噪声间的互相关强度λ不同的情况下，稳态概率密度函数Pst关于蛋白质浓度x的函数图像。如图4所示：互相关强度λ=0.13时，稳态概率密度主要分布在低浓度状态，基因处于“关”状态。随着λ逐渐增加到0.93，稳态概率密度在低浓度状态下的峰值逐渐减小到0，同时在高浓度状态处出现峰值，并且峰值逐渐增加。换句话说，基因从“关”状态完全过渡到“开”状态。所以噪声间的互相关强度λ对基因的转录效率和“开-关”机制也有很大的影响。

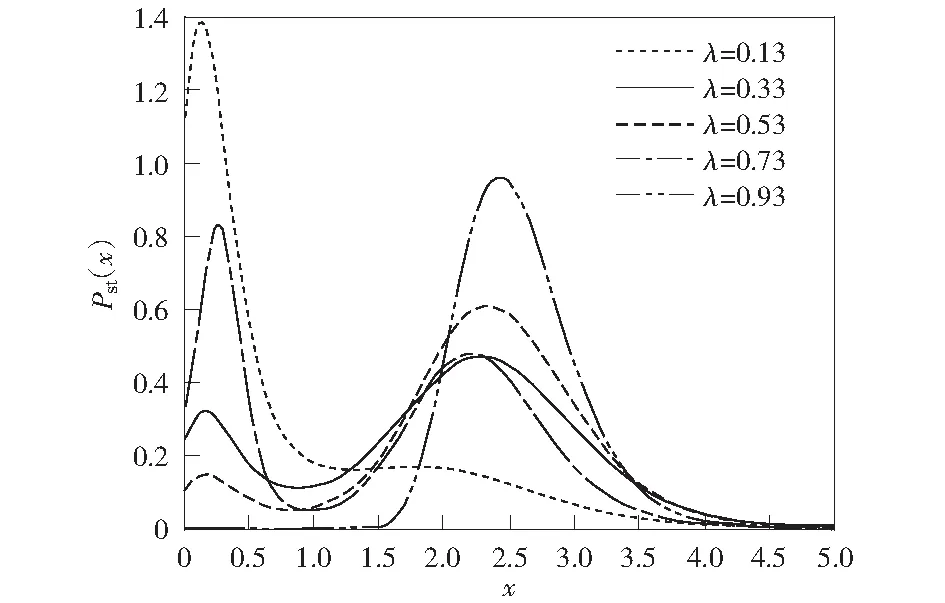
μ=0.1, k=5.0, β1=1.0, β2=1.8, q=0.8, D1=D2=0.03, τ1=τ2=0.3图4 不同噪声间的互相关强度λ下概率密度函数Fig.4 Stationary probability distribution for different λ

3 结束语

近些年，大量的生物学研究指出了基因调控与人类重大疾病的发生息息相关。BALTAZAR et al的研究表明转录因子在基因调控过程中既可以作为抑癌基因，又可以作为致癌基因，这主要由它们的表达水平决定。本文通过随机动力学的方法研究了噪声在基因调控过程中对转录因子的影响，得到非高斯噪声强度、偏离高斯噪声程度以及噪声间的互相关强度在一定条件下不仅能够影响基因调控的表达效率，还能使基因转录表达在低浓度稳态和高浓度稳态间转换。同时，也期望本文的成果能为基因调控的研究以及癌症的治疗提供一个理论基础。