学习全局边函数的半监督社区检测

丁彩英，李泽鹏，刘松华，3

(1.太原理工大学 信息与计算机学院，山西 晋中 030600；2.兰州大学 信息科学与工程学院，兰州 730000； 3.北京大学 信息科学与技术学院，北京 100871)

现实生活中众多复杂系统都能用网络进行建模，如社交网络、经济网、生物网络等。而随着在线网络信息量激增，获取的各种属性等数据越来越多。如何理解这些网络的内在机制，并有效利用这些数据成为当前社区检测领域的重要研究热点。

检测社区允许我们发现与对象相关的功能，研究模块之间的关联，推断丢失的属性值，预测没有观察到的连接等。传统的社区检测中，所谓的社区一般是保证组内的边的连接密度高于组间[1]。如在线社交网络中，社区对应一组朋友，他们就读于相同的学校或者来自相同的县市。蛋白质相互作用网络中，社区对应相互作用的蛋白质之间的功能模块。协作网络中，社区对应学科分类。

从建模模型角度分析，传统的社区检测算法可以分为两类：1) 概率模型，如SBM(stochastic block model)模型[2]、Dirichlet模型[3]等；2) 谱近似模型，如模块度[4-6]、及其它的谱聚类[7]、矩阵分解类[8-9]等算法。目前，已有社区检测算法已经取得了巨大成功，在各行各业都有具体的应用。但由于已有算法大多数均基于聚类的无监督版本，唯一可利用的信息就是图结构，通常考虑图的邻接矩阵，无法有效挖掘潜在的社区形成和发展的机制。因此不可避免会碰到如下问题：1) 噪声问题，如数据的获取方式本身会带来各种干扰信息；2) 不同的检测算法产生不同的解，如分别从节点和边的角度进行检测会产生不同的社区。

近年来，随着网络数据获取能力的提升，出现了大量可用数据。针对社区挖掘面临两大挑战：1) 可用数据以指数级增长；2) 数据标注任务繁重且昂贵，同时需要专家参与。因此国内外学者开始以半监督学习的方式进行社区挖掘，在现实网络中，除了网络拓扑信息外，可能会有特定节点聚类归属的信息。主要包括两类[10]：1) 节点类别、属性等信息；2) 成对约束(必连和必不连)。

从节点等信息分析，文献[11]提出了利用部分节点语义信息进行社区检测的方法，该方法可以用于检验先验知识对检测阈值[12]的影响程度。文献[13]提出了基于密度的自适应聚类方法，结合节点类别控制密度区域参数的选取。文献[14]基于非负矩阵分解提出了一种结合节点重要程度的学习方法。文献[15]结合离散势理论进行半监督社区检测，但仅限于无重叠类型，不考虑多条边，且要求每个社区至少有一个有类别的节点。文献[16]提出了将网络结构和节点特征结合的社区检测算法，有别于其它工作，它可以检测重叠社区。但是上述方法没有考虑节点特征的重要性，因此文献[17]提出了判别节点特征的重要性并结合邻接矩阵进行社区检测的方法。

从成对约束分析，文献[18]将主动学习引入社区检测问题中，利用主动学习来生成必连和必不连约束，然后进行半监督社区检测。文献[19]将成对约束结合到邻接矩阵中，并采用NMF(non-negative matrix factorization)、谱聚类、InfoMap等方法，结合降噪的一致矩阵进行半监督社区检测。文献[20]提出了基于对称非负矩阵分解的半监督方法，该方法将成对约束结合到邻接矩阵中寻找社区结构，并证明了模块密度与对称非负矩阵分解的等价性。在此基础上，文献[21]添加一个逻辑推断步骤来利用必连和必不连约束，最后进行半监督学习。

除了上述工作外，有学者结合节点和边的内容进行社区检测，如文献[22]提出节点属性等信息与真实类别之间的关联，证明了节点等先验知识对社区检测的重要作用。文献[23]提出了基于连接的主动监督信息获取框架，主动选择集线器节点所连的边并断开社区间的边，最后以文献[19, 21]提出的半监督社区检测方法为基准进行比较。

值得注意的是，上述半监督社区检测方法都是将有类别信息的数据编码并将先验信息转化到拓扑信息中，通过直接转换和修改邻接矩阵来使用先验知识。但存在一个主要的缺陷是无法有效利用必连先验，因此会存在诸如直接连接的节点不能保证分配到相同的社区等问题，而且这些方法通过修改网络拓扑，将半监督转化为了传统的无监督学习，半监督作为社区检测的预处理，没有使用半监督的本质特性。因此文献[24]提出了一种统一框架，将NMF和谱聚类统一到一个框架下进行半监督学习，但是没有对先验知识的重要性进行提取。

为了解决上述问题，有效利用现有网络内的各种信息，基于文献[10]的自旋玻璃模型(SG,Spin-Glass)和文献[6]的模块度优化模型，本文提出了新的半监督社区检测算法(SSE,Semi-supervised community detection based on global edge function learning)，该模型能够将网络拓扑信息、节点属性、边属性等信息或者其它有用的先验知识结合到社区检测中，能针对特定的需求有效引导社区发现过程，最大程度提升半监督学习的社区检测性能。

1 学习全局边函数的半监督社区发现

本节针对上述半监督学习面临的问题，提出从3个方面结合属性等信息完成社区发现，首先引入节点属性信息和部分类别信息。其次引入必连和必不连成对约束条件。最后引入网络的拓扑信息，从三个层面不断优化。

1.1 问题描述

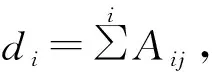
本文的任务是结合边属性、节点属性或者部分已有类别等可利用信息来预测每个未标注节点u(u∈U)的合理的类别r.

1.2 融合边函数的目标函数

模块度[6]用来衡量网络中一个划分的质量，是社区检测中普遍采用的方法。该度量从全局视角测度图中获取的社区结构，其主要思想是假定一个没有社区结构的空模型，进而采取谱分解的方法来优化模块度函数。设Q是一组社区C的模块度，则其计算公式如下：

(1)

式中：Pij表示空模型中节点vi和vj之间存在一条边的概率；Ck表示节点vk所属的社区；d(Ci,Cj)是Kronecker delta函数，如果节点vi和vj属于相同社区，其值为1，否则为0.

NEWMAN et al[6]采用的空模型如下：

(2)

该模型保持总的边数和度分布不变，对给定的图进行重新连接，构成了空模型。

然而，随着属性网络的出现，如何将属性结合到社区发现过程中成为了重要的研究方向。YANG et al[24]指出合适的采用各种属性信息能极大提高社区发现的质量，并有效提升发现社区的可解释性。因此本文在公式(2)空模型的基础上，定义新的模型如下：

(3)

一旦公式(3)中所示改进空模型确定，则根据自旋玻璃模型SG[10]，将公式(1)对应的模块度优化问题转化为波茨模型的汉密尔顿最小化问题：

(4)

其中g参数与文献[10]中计算相同。

1.3 边函数学习

采用公式(3)的主要目的在于将现有信息直接结合到目标函数中，如文献[18-21]中涉及的必连和必不连信息。本文可以对边函数采用两种学习方法：设置为核函数或者用半监督聚类学习边函数。

1.3.1 直接设置为核函数

与文献[25]的边函数设置不同，本文将边函数定义为核函数[26]，形式如下：

kij=w(vi,vj)=〈j(vi),j(vj)〉 .

(5)

由公式(5)即可计算相应的边函数，采用上式的原因有两点：1) 根据文献[5]，模块密度计算目标函数等价于核k均值聚类，因此本文可以很方便地推广到模块密度；2) 根据文献[26]，其中的低秩近似方法在应用于大规模图时能有效降低时空复杂度，提高算法的推广性能。

1.3.2 半监督聚类边函数学习

设图中每个节点vi∈Rd表示一个d维向量，包含了节点的各种属性等信息。M为必连约束集合(vi,vj)∈M表示节点vi和vj属于相同社区；CN为必不连约束集合(vi,vj)∈CN表示节点vi和vj属于不同社区。F∈{0,1}n×n为二值矩阵，表示n个节点划分到最多n个社区。对于所有可能的社区划分结果表示如下：

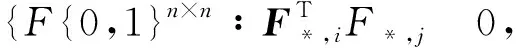
(6)

其中Fl,*和F*,j表示矩阵第l行的向量和j列的向量。

基于以上背景，公式(3)中的边函数可以设置为F，使得其与学习到的K尽可能一致。因此需要测度两者之间的偏差，采用如下距离：

(7)

除了满足公式(7)的条件，还需要测试F与约束条件的一致性，因此引入两个损失函数，必连约束的损失函数定义为Loss-(Fi,*,Fj,*)：

(8)

同理，必不连损失函数定义为Loss+(Fi,*,Fj,*)：

(9)

结合公式(7)和损失函数，可以将上述半监督学习转化为如下的优化问题：

(10)

综上，采用文献[27]的方法求解公式(10)，可以获取到公式(3)所需的边函数w=F.

1.4 半监督社区发现算法

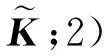
经过半监督学习框架获取的目标矩阵为P，其对应的元素为Pij。据此，本文采用矩阵分解的方法对P求解如下优化问题并进行社区检测。

(11)

其中P为公式(4)优化后的目标矩阵，U为社区类别归属矩阵，大小为n×r，表示n个节点分别属于r个社区，公式(11)的求解采用算法SBMF的思路进行。

最后，本文提出的半监督学习算法整体框架如下。

算法1:学习全局边函数的半监督社区发现框架(SSE)输入:邻接矩阵A,已知部分类别信息节点集合L,包含属性的节点集合V,成对约束必连条件M和必不连条件CN,节点类别数目r输出:类别归属矩阵U1:引入节点属性V和部分类别信息L求解核矩阵,根据公式(5)结合文献[26]的T-SLKMS方法输出K2:引入成对约束条件M和CN求解边函数F,根据公式(7-10)结合文献[27]的方法输出F3:引入图拓扑信息A求解矩阵P,根据公式(3,4)结合文献[10]的方法输出P4:采用矩阵分解方法对P进行求解,根据公式(11)的方法输出U

2 仿真分析

为了证实本文提出算法的有效性，本文与已有的算法进行比较：无监督的SBMF算法、半监督自旋玻璃模型SG[10]、半监督NMF_LSE算法[24]。数据采用人工数据GN，真实数据采用Karate，Dolphins，Football，这些数据均为上述方法采用的公开数据。最后用结合真实数据的合成赣南客家数据进行了测试，结果采用10次平均，其它均采用50次实验的平均值与标准差标注。

评价算法性能除了从社区分类正确率和F测度[10]来分析，还采用了通用的规范化互信息NMI来衡量。

2.1 人工合成数据GN实验

GN(Girvan-Newman)网络数据是测试社区检测算法的一类基准数据集，划分示意图如图1所示。网络包含128个节点、4个社区，每32个节点划分为1个社区，每个节点与Zin个社区内和Zout个社区间节点随机连接生成平均16条边，即Zin+Zout=16.对于每对Zin与Zout随机生成10个网络，实验结果显示随着Zout的增加，网络结构变化复杂，难以有效检测社区。

与文献[24]的NMF_LSE比较结果，可得如下结论：1) 与SBMF同样，本文算法能有效获取GN网络的真实社区划分；2) 与NMF_LSE比较，本文能在Zout=6，先验知识使用10%的时候将真实社区划分出来，见图1(b)所示，与NMF_LSE性能接近。3) 随着Zout的增加，网络会变得难以划分，当达到8时，仅仅使用拓扑信息无法有效发现社区，而SSE算法与NMF_LSE算法仍然能有效检测真实社区，且SSE在先验知识使用10%时能检测出4个社区，相比NMF_LSE性能稍高。4) 本文SSE算法在使用先验知识达到26%的时候NMI=0.882±0.101，因此本文算法从一定程度上可以避免分辨率极限问题，也表明了先验知识对社区划分的重要影响。

图1 GN合成数据划分示意图Fig.1 Sketch map of GN compose data

SBMF仅给出了正确检测社区数，而文献[10]由于作者没有在GN上进行测试，因此没有与其对比。

2.2 真实数据实验

Karate数据包含34个俱乐部成员作为节点，78条边表示成员之间的关系。划分示意图如图2所示。由于俱乐部管理员和教练之间的分歧，俱乐部一分为二，分别由上述两人带领各自团队组建。Dolphins该数据包含62个海豚，159条边。划分示意如图3所示。Football数据有115个美国足球队，613条边。划分示意如图4所示。节点表示足球队，如果两队之间有比赛则有边连接。该数据已知的信息是足球队被分为12个大型比赛，在某个比赛中足球队通常与多个其它对进行比赛。FaceBook数据有10个自我网络(ego-networks)，包含193个社交圈和4 039个节点，88234条边，网络的平均聚类系数为0.605 5，该网络为无向图，每个节点包含26个属性(包括家乡、生日、同事、政治面貌等)。

与NMF_LSE实验结果表2比较，本文算法SSE在Karate上算法与其类似，在dolphins算法上性能较高，主要原因在于SSE有效的特征提取性能，但当先验知识使用比例增大时，NMI值会不同程度下降，检测的社区数目会增加，存在过度学习问题。与SG实验结果fig1比较，在上述两个数据结果类似，体现了半监督的独有特性。

与SBMF实验结果fig6(a)比较，本文算法SSE在检测到社区数目为11和13时均有较高的NMI值，但与NMF_LSE算法结果Table II比较可知，在该数据集上的NMI值相对较低。同时发现在社区检测数目增多的时候，可能能检测出新的有意义的社区，如图2(b)、3(b)、4(d)，一定程度上可以表示社区演化结果。SBMF算法在分解的过程中引入惩罚项控制分辨率极限问题。而SG，NMF_LSE方法则受限于监督信息的获取。本次实验中SBMF可以看作本文算法的后处理阶段。

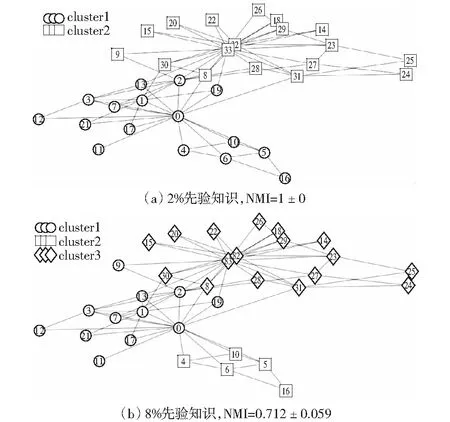
图2 Karate数据划分示意图Fig.2 Sketch map of Karate data to divide

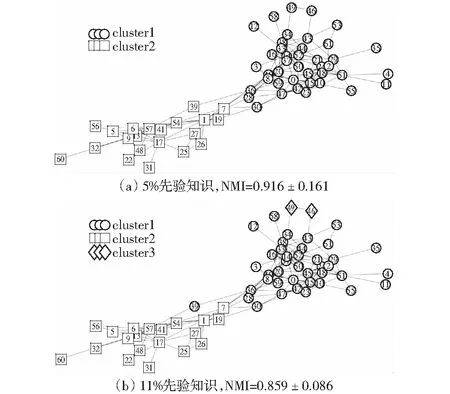
图3 dolphins数据划分示意图Fig.3 Sketch map of ddphins data to divide

为了验证本文算法在数据量较大时的有效性，以赣南客家群落为研究对象，研究其迁徙地属性特征对迁徙后群落形成的影响，并进一步探讨群落分类。由于客家数据目前仍在整理阶段，因此本文模仿LFR合成数据，主要用于测试不同社区节点数目不同以及节点度数差异较大的网络结构问题。数据生成器允许指定节点数目、平均度数、社区大小分布、度分布、最小最大社区大小、重叠比率。LFR中社区大小和度分布都服从幂率分布，通过抽样的方式生成节点和社区。本节实验中，节点数目设置为201 8，社区数目为13，平均度为10，节点度和社区大小的幂指数分别为-2和-1，重叠比率为0.1～0.5，并将平衡参数设置为1。表1中给出了本文算法在赣南客家网络上的实验结果，由于运行时间较高，因此最终结果取10次实验的平均值。数据集生成时模拟Facebook引入属性，分别是赣南水系(空间：长度、流向、落差，特征：江、河、湖)、赣南地形(面积，特征：丘陵、山地)、耕地(山地、平原)、道路(村、省、国道)等14个特征属性，属性根据生成数据时的聚类或分类分别加入，属性加入服从常见高斯分布，数据生成时间为东晋南北朝末第一次大迁徙到唐末中期第二次大迁徙阶段。

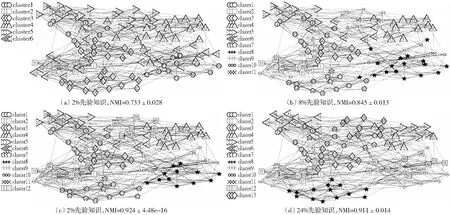
图4 football数据划分示意图Fig.4 Sketch map of football data to divide

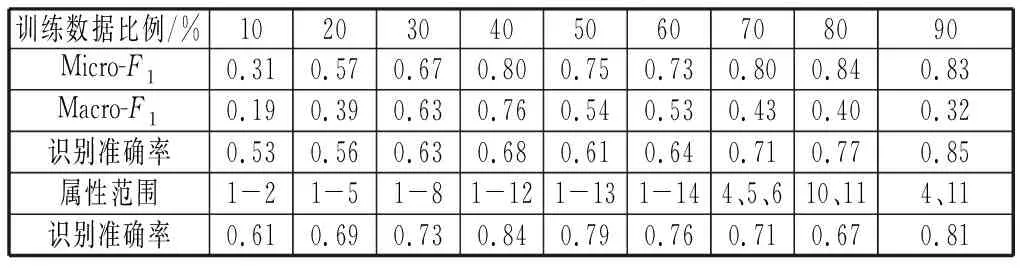
表1 在合成赣南客家数据集上进行测试结果Table 1 Test result of Gannan Hakka

表1中，本文算法主要考虑引入类别知识后边的必连和必不连信息，同时考虑先验知识中的节点属性。分析F测度，Micro-F1基本呈现递增趋势，Macro-F1则无此规律，可见训练数据集的选取对算法性能有较大影响，同时也说明了数据中存在较大的冗余。同时从表1中发现，单单分析社区识别准确率，SSE算法在使用训练数据方面，随着使用比例加大识别率会单调递增。而采用所有数据后，对于不同属性，识别准确率呈现多样性，并不会随着属性增加识别率单调递增，表明算法加入的属性有类似噪声的作用。所以，对属性提取后，选取江、河、湖(4，5，6)，山地、平原(10，11)以及江、平原(4，11)计算识别准确率，结果发现水系对赣南客家迁徙相比于耕地对迁徙意向起了较多的影响，而水系和耕地结合则更能影响迁徙路径，因此迁徙中地理环境对赣南客家人有较为重要的作用。

3 结束语

本文提出的半监督策略，能有机结合已有先验知识，获取全局最优解，但对数据要求较高，在人工和真实数据上的仿真实验结果表明提出的方法具有较好的效果和可扩展性。下一步工作将集中在各类附加信息在动态社区检测中的影响及应用，以及对网络各类型数据的降解工作，便于处理海量数据。

本文给出了一种新的验证赣南客家迁徙的思路，生成的实验数据可以说明迁徙中的部分影响因素，下一步工作集中在数据生成器，在设计时应该考虑度分布与属性分布相结合，同步生成可能更切合实际情况。