分别基于接近性和相似性的面板数据关联度的公理化
王 慧,魏 勇
(西华师范大学 数学与信息学院,四川 南充 637009)
0 引言
灰色关联分析是灰色系统理论的一个重要分支,它对作用对象的数量和有无规律性没有要求,计算量小,弥补了采用传统数理统计方法时导致的缺点[1]。学者们以邓聚龙的灰色关联四公理为理论基础,基于不同研究对象的实质,提出了不同类型的灰色关联度,如邓氏关联度、灰色B型关联度、灰色绝对关联度、灰色C型关联度等。但对于现实而言,数据的复杂程度决定了学者们应着力于灰色关联分析在多指标的面板数据中的应用研究。观察相关文献[2-6]可以发现,应用于面板数据时学者们基于不同的理论点提出了不同的关联度计算方法,相似性关联度和接近性关联度是其中的核心部分,已有的文献暂时没有一个可以公理化这两大类关联度计算式的定义,不能清楚地说明各种关联度可以反映哪种实际应用,从而导致其他方向应用关联度时因为概念混淆而错误判断关联程度。在此基础上,文献[7]指出对于时间数据序列而言,不可能定义一个既能反映相关性又能反映接近性的关联度,应分门别类地讨论相似性和接近性关联度。而且很多关联度计算式在满足邓氏关联四公理的规范性前提下不能均匀分布在[0,1]区间内,导致结果的辨析程度较差,出现多个关联度间结果差距较小,或者差距太大,不能较好反映序列间关联程度差异。
针对以上情况,本文首先提出了一种新的面板数据初始化方法,能较好地反映数据在均值附近波动的情况,从而便于观察数据序列间变化形式的相似性,其次分别公理化了面板数据的接近性关联度和相似性关联度并给出案例,探讨了在规范性前提下利用分辨系数ξ(0<ξ<+∞)来拓展关联度取值分布,提高了对结果的辨析程度,最后通过实例分析来说明结论的可靠性。
1 准备知识
1.1 面板数据的矩阵表示
面板数据也叫平行数据,是指在时间序列上取多个截面,在这些截面上同时选取样本观测值所构成的样本数据,区别于传统的单指标时间数据序列,面板数据具有时间维度、指标维度和样本维度,是多样本多指标时间序列。对面板数据进行关联分析首先要了解其数学表达,设样本总体数量为N,指标数量为m,时间长度为n,文献[2]采用三维数据表来描述面板数据,由于数据表不能体现出面板数据的几何特征,故将二维表中的值对应为三维坐标中的点,将其在三维空间中每一个点记作xi(s,t),表示样本i关于指标s在时间t处的值。
定义1[2]:若面板数据X中的样本i关于指标s在时间t的数值为xi(s,t),则称

为样本i的行为矩阵。
定义 2[6]:面板数据序列X=(X1,X2,…,XN)为其样板序列,将面板数据投射到n维空间中的n维向量,则设样本序列中的Xi满足:
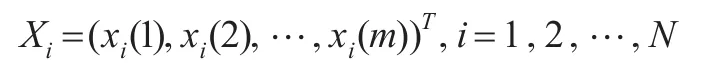
其中xi(s)=(xi(s,1),xi(s,2),…,xi(s,n)),s=1,2,…,m,称xi(s)为这组面板数据中样本i关于指标s的时间序列。
1.2 新的面板数据初始化方法
定义3:Xi是样本i的面板数据,D是初始化算子,若:
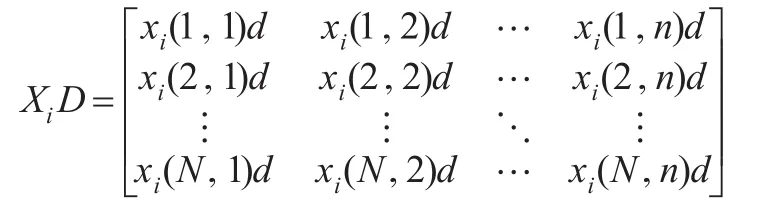
灰色关联分析基本思想中的两大类,一是根据时间数据序列曲线几何形状的相似程度来判断其关联程度大小,二是根据时间数据序列的接近程度来判断其关联程度大小,对于空间中的向量而言,一方面向量夹角越小其相似程度越高,其关联程度也越大,另一方面两向量之差的模长越小,则越接近关联程度越大,因此可以利用向量夹角和向量差的模长来描述相似性和接近性关联度。
定义4:设样本i与样本j在s指标下通过均值波动算子初始化后的的时间序列为:

则两指标序列的夹角为:
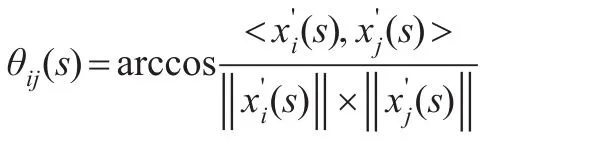
值得注意的是利用向量差的模长计算接近性关联度来判断序列间关联程度大小是不能用均值波动算子处理数据的,因为均值波动算子会改变原向量在空间中的位置及距离。
2 主要结果
2.1 基于面板数据的接近性关联度的公理化定义与具体构造示例
定义5(面板数据的接近性关联度):设面板数据序列为X=(X1,X2,…,XN),其中X0=(x0(1),x0(2),…,x0(m))为系统特征序列,Xi=(xi(1),xi(2),…,xi(m)),i=1, 2,…,N为系统比较序列,且Xi(s)=(xi(s,1),xi(s,2),…,xi(s,n)),s=1,2,…,m。若实数γ(Xi,Xj)满足:
(1)规范性:0<γ(Xi,Xj)≤1 且γ(Xi,Xj)=1⇔Xi=Xj即γ(Xi,Xj)=1⇔Xi(s,t)=Xj(s,t),s=1,2,…m,t=1,2,…,n;
证明:(1)规范性:
显然 0<γ(Xi,Xj)≤1,还需证明γ(Xi,Xj)=1 ⇔Xi=Xj⇔Xi(s,t)=Xj(s,t)s=1,2,…,m;t=1,2,…,n。
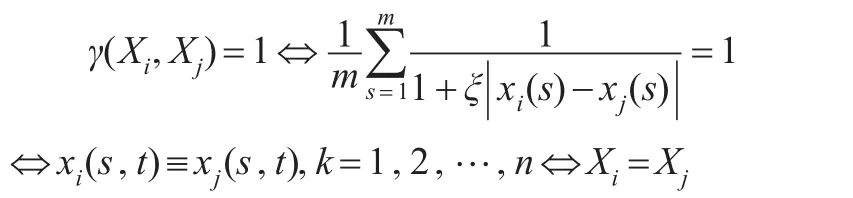
(2)接近性:
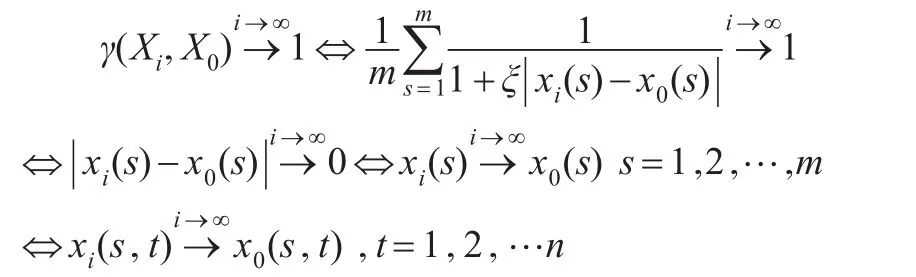
可以发现案例中的接近性关联度使得除了完全相同的两面板数据在任何分辨系数下关联度为1保持不变以外,其他任何不同的两面板数据都会随着分辨系数增大而关联度值减小,随着分辨系数减小而关联度值增大,从而起到了调节辨析率的作用。
此处分辨系数ξ为0<ξ<+∞,并建议根据具体研究对象的实质以及计算出的关联度差异来动态地确定ξ的取值。如当计算出的两不同方案数据序列关联度值均接近于1时接近程度高,不易辨析其二者差异时,可通过分辨系数动态地取值来调节差距,这时分辨系数ξ越大,关联度值就越小,就如同放大镜来放大差距,提高辨析程度。分辨系数ξ越小,关联度值就越大,且关联度值越接近于1,就越来越淡化其差异,肯定其接近程度,如果允许ξ=0,则将完全抹杀所有序列之间的差异,关联度值衡为1,从而是一种毫无意义的关联度。
值得注意的是:接近性关联度不能对数据进行初值单位化、零像化等操作,因为初值单位化会抹杀对应项成比例的两序列之间的差异,初值零像化会抹杀序列各坐标平移某固定常数前后之间的差异,均会导致对应坐标相聚甚远而关联度值较大的情形,这就必然失去通过计算其接近性关联度来判断关联程度大小的真实性。
2.2 基于面板数据的接近性关联度的公理化定义与具体构造示例
定义6(面板数据的相似性关联度):设面板数据序列为X=(X1,X2,…,XN),其中X0=(x0(1),x0(2),…,x0(m))为系统特征序列,Xi=(xi(1),xi(2),…,xi(m)) ,i=1,2,…,N为系统比较序列,且Xi(s)=(xi(s,1),xi(s,2),…,xi(s,n)),s=1,2,…,m。若实数ρ(Xi,Xj)满足:
(1)线性相关规范性
0<ρ(Xi,Xj)≤1且ρ(Xi,Xj)=1⇔∀s=1,2…,m,∃αsi≠0,βsi满足Xi=αsiXj+βsi;即ρ(Xi,Xj)=1⇔∀s=1,2…,m,∃αsi≠0,βsi使xi(s,t)=αsixj(s,t)+βsi,t=1,2,…,n
(2)线性相关接近性:
ρ,∃αsi≠0,βsi满 足αsi,即≠0,βsi满足:则称ρ(Xi,Xj)为面板数据样本序列中Xi与Xj的相似性关联度。
证明:(1)线性相关规范性:
显然,0<ρ(Xi,Xj)≤1,还需证明ρ(Xi,Xj)=1⇔∀s=1,2…,m,∃αsi≠0,βsi满足Xi=αsiXj+βsi,即ρ(Xi,Xj)=1⇔∀s=1,2…,m,∃αsi≠0,βsi使xi(s,t)=αsixj(s,t)+βsi,t=1,2,…,n
先证必要性:
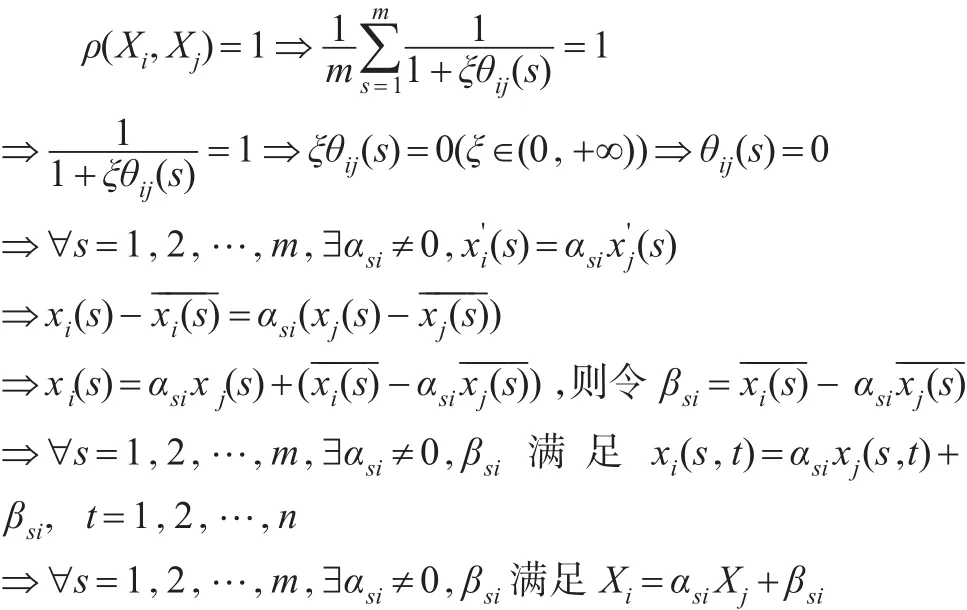
再证充分性:

即ρ(Xi,Xj)满足线性相关规范性。
(2)线性相关接近性:
先证必要性:
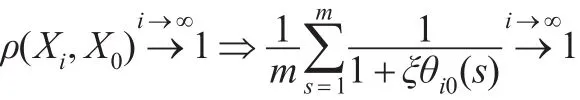
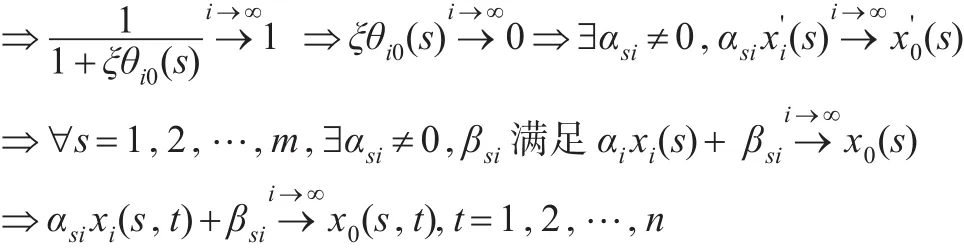
再证充分性:
∀s=1,2,…,m, ∃αsi≠0,βsi满足(s,t)
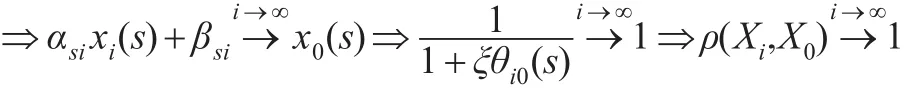
即ρ(Xi,Xj)满足线性相关接近性。
此处分辨系数ξ仍然为0<ξ<+∞,也建议根据具体研究对象的实质以及计算出的关联度差异来动态地确定ξ的取值。当一组并不完全线性相关的数据序列计算出的关联度值均不等于1但接近于1时,不易辨析,可通过分辨系数动态地取值来调节差距,这时分辨系数ξ越大,关联度值就越小。分辨系数ξ越小,关联度值就越大,关联度值越接近于1,就越来越淡化其并不完全相关的事实。另外,与接近性关联度一样决不允许ξ=0。
值得注意的是:相似性关联度与接近性关联度相反,能容忍对数据作平移和数乘变换,因为两序列各自平移、数乘任意常数不影响线性相关程度。
3 实例分析
案例1:设西部某省A、B、C、D四市在一项政府新政策下达后2014—2016年平均每户家庭每月在饮食、旅游、教育上的金额如下(单位:千元),X0为A市面板数据,X1,X2,X3为B、C、D市的面板数据,若想要以此探讨此项新政策对四市的经济发展情况的影响,应如何运用灰色关联分析?
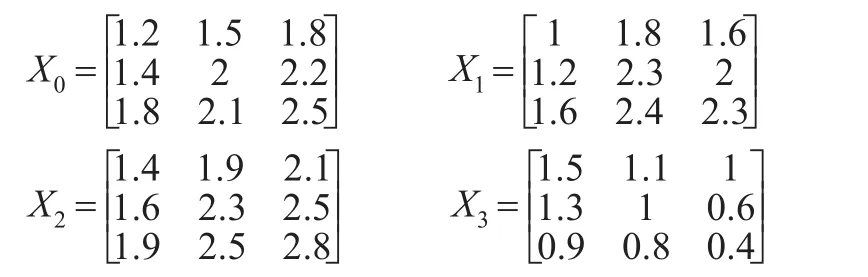
首先应分析题意,选择接近性或者相似性关联度,题中描述此面板数据体现的是在该项新政策影响下平均每户家庭每月在饮食、旅游、教育上的金额的变化情况,强调在该政策下不同市之间每户家庭在不同指标下金额的变化情况的相似性,而不是消费水平的接近性,所以应采用相似性关联度来计算,本例即选取例2的相似性关联度:
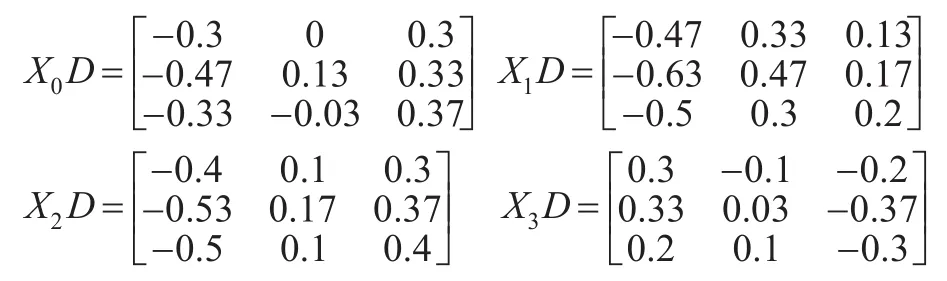
经过均值波动算子处理后的面板数据为:取ξ=1时通过改进的关联度计算得到:ρ01=0.6032 ,ρ02=0.8522 ,ρ03=0.2947
即从关联程度上看,有ρ02>ρ01>ρ03,且从时间维度上观察面板数据初始化后在每个指标下的时间序列,X0与X2的变化趋势确实比X0与X1的变化趋势接近,X0与X1的变化趋势也确实比X0与X3的变化趋势更接近,结果与实际相符,另本例中设出的数据与文献[6]的相同,得到的结论也是一样的,更加说明此例中采用的关联分析的正确性。
案例2:现有A、B、C、D四省在2014—2016年平均每户家庭每月在饮食、旅游、教育上的金额如下(单位:千元),X0为A省面板数据,X1,X2,X3为B、C、D省的面板数据,若需要以此为依据分析A、B、C、D四省的经济发展情况,该如何利用灰色关联分析?
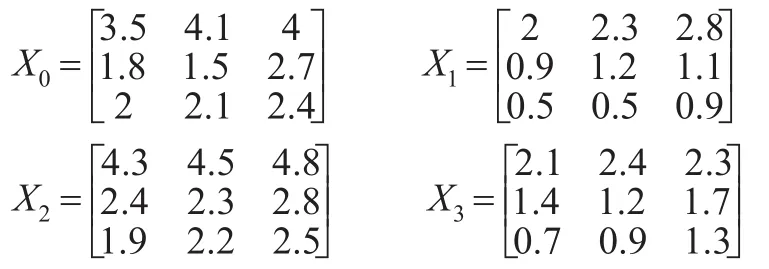
首先分析题意,选择接近性或者相似性关联度,题中描述的面板数据是平均每户家庭每月在饮食、旅游、教育上的金额,强调的是西部四个不同省份之间每户家庭在饮食、旅游、教育三个指标下消费水平的接近性而不是相似性,所以应采用接近性性关联度来计算,本例即选取例1中的接近性关联度,因为是探讨的接近性,所以不能对数据进行初值单位化、零像化等操作,取分辨系数ξ=1,直接利用式子计算后得:
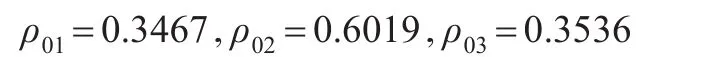
即从关联度来看ρ02>ρ03>ρ01,从分指标的时间序列来看,确实C省的数据与A省更接近,但B、D两省与A省计算出的关联度太接近,可尝试适当调节分辨系数来增强辨析性,当ξ=1.5时,有ρ03=0.2649>ρ01=0.2702,增大了二者之间差值,但关联序没有变化,更说明了D省与A省的关联程度比B省与A省的关联程度大。
4 总结
本文主要作了以下几方面工作:
(1)提出了基于面板数据的接近性和相似性两类性质炯然不同的关联度之公理化定义,举出的接近性或相似性相应类型关联度的实例仅仅是示范,并不唯一;
(2)给出一种的面板数据初始化方法,但并不是硬性要求,因为初值化与否并不影响关联度值的计算结果;
(3)强调通过适当添加分辨系数来调节关联度,此时分辨系数应是动态的,提高关联度的辨析性,分辨系数不局限在(0,1),而是所有可能的正数;
(4)就接近性关联度和相似性关联度在实际中的应用分别给出实例,并解释采用哪种类型关联度的原因,为之后的针对应用问题的相关实质选择所需关联度提供参考示例。

