多臂空间机器人操作大型目标的全身接触柔顺控制研究

刘嘉宇， 李通通， 余张国， 陈学超， 黄强

(1.北京理工大学 机电学院, 北京 100081； 2.中国运载火箭技术研究院 北京精密机电控制设备研究所, 北京 100076)

0 引言

以空间机器人为代表的智能无人系统作为人类的代理，将在未来空间应用中成为主力，而空间机器人的操作能力作为未来“抓”、“修”、“建”等应用的重要组成，具有重要的研究价值和意义。Yoshida等[1]早在20世纪90年代就开展了空间机器人在轨操作的应用——研究工程试验卫星(ETS-7)，美国国防高级研究计划局(DARPA)开展了轨道快车任务[2]、德国/加拿大/俄罗斯宇航局(DLR/CSA/RKA)合作开展了空间系统演示验证技术卫星项目(TECSAS)[3]、DLR开展了德国轨道维修任务(DEOS)[4]，但是这些研究并未考虑大型目标特性带来的挑战。美国DARPA 的凤凰计划[5]是典型的大型目标操作任务，其目标质量是机器人的4倍，但其技术细节鲜有文献公开发表。

大型目标给机器人捕获带来两个挑战：首先，操作大型目标时，由于负载惯量过大，机器人难以对目标进行有效的约束，而是在目标拖拽力的牵引下跟随运动；其次，目标的翻滚运动会导致把手的运动轨迹比较复杂，而目标动力学参数的未知性更加剧了被牵引运动的复杂性。因此，机器人操作大型目标极具挑战。另外，与单臂机器人相比，多臂机器人具有更强的操作能力，极大地拓展了在轨服务能力的上限。有学者开展了面向空间翻滚目标捕获的研究[6-9]，但均未针对大型目标特性展开讨论。显然，随着目标与机器人质量比的增大，机器人在捕获和操作过程中将处于越来越被动的地位。

另外，接触安全也是大型目标捕获和操作研究中极具挑战性的问题，阻抗控制方法给柔顺接触问题提供了良好的解决思路，最早由Hogan[10]于1985年提出，已经得到了广泛应用和拓展。Rastegari等[11]提出了基于虚拟连杆的多臂空间机器人阻抗控制方法，能够对多臂协同操作产生的内力进行有效管理。Stolfi等[12]提出了一种阻抗加比例- 微分(PD)组合控制方法，用来控制双臂空间机器人操作的非合作目标。然而，这些方法均未针对性考虑大型目标特性带来的挑战。

为了应对来自大型目标的拖拽，机器人需要尽可能利用自身有限的运动能力对目标实施操作。因此，机器人不仅需要产生合适的全身柔顺行为以避免支撑臂应力过大，还需要在该过程中将外部拖拽力有效地分配到多个支撑臂中，从而尽可能减少单点过应力，进而提升系统生存空间。

本文针对多臂空间机器人操作大型目标时面临的挑战，提出一种全身接触柔顺策略，旨在有效降低操作风险、提升操作安全性和成功率。该方法兼顾考虑了全身阻抗控制、多臂力分配、单臂独立导纳控制和关节力矩优化等要素，并利用二次规划(QP)方法构建了具有一定开放性的多目标动态规划框架。最后，通过仿真和基于气浮的物理实验综合验证了上述方法的有效性。

1 空间机器人操作大型目标模型

1.1 多臂空间机器人建模

如图1所示，多臂空间机器人是一个典型的树形、多刚体、铰链体结构，由本体和多条挂载其上的机械臂组成。

图1 多臂空间机器人操作大型目标示意图Fig.1 Schematic diagram of multi-arm spatial robot manipulating a large target

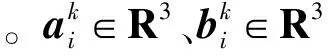
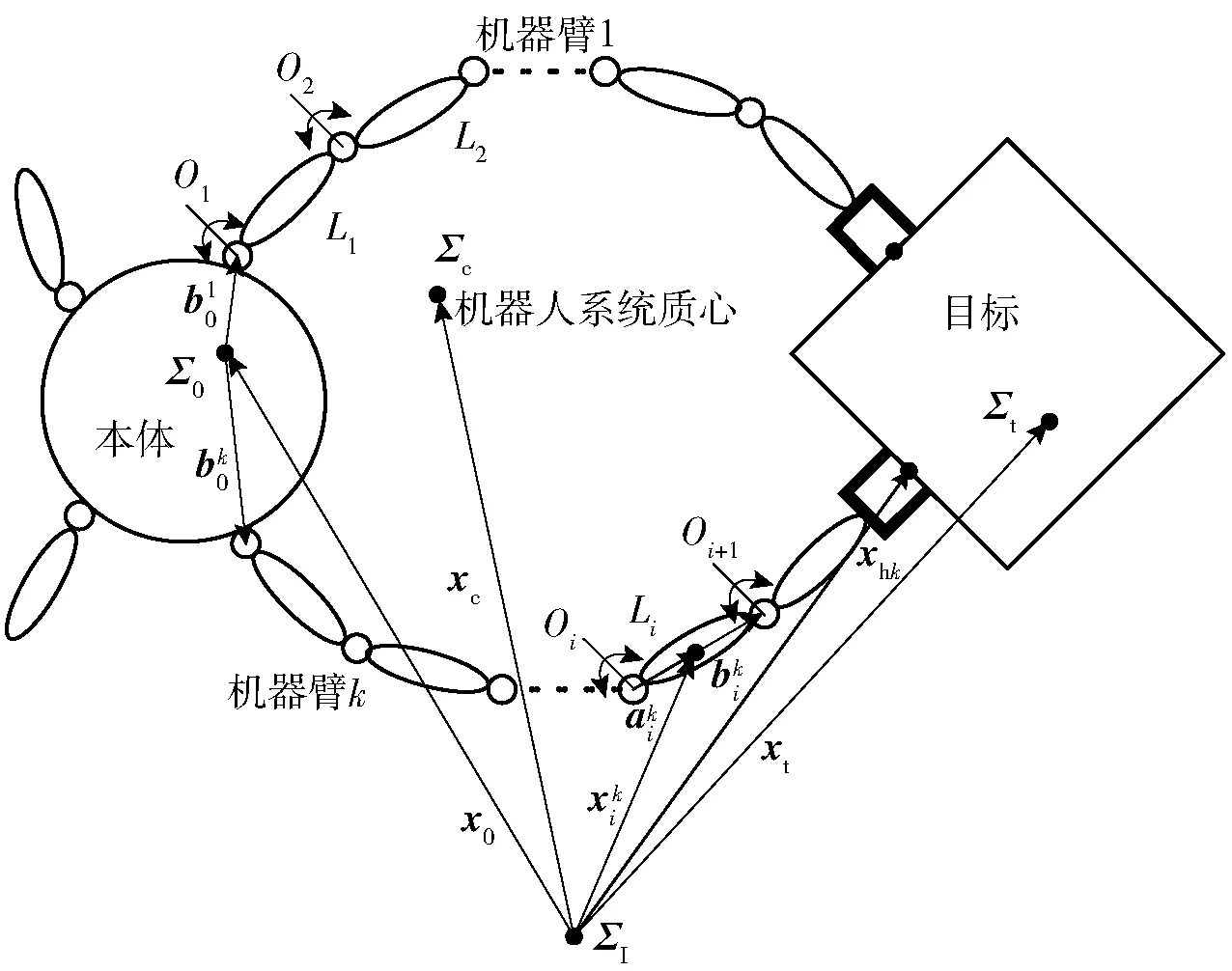
图2 多臂空间机器人操作目标示意图Fig.2 Model of robot contacting with target

1.2 系统CoM

多臂空间机器人的CoM位置是关节变量的函数，满足如下关系：

(1)

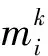
(2)

求解(1)式和(2)式，可得CoM的位置矢量表达式：

(3)

式中：Σc与Σ0的姿态矢量φb∈R3一致，φb可由本体在ΣI下的姿态测量确定。因此，多臂空间机器人CoM的广义位置可定义为

(4)

1.3 动力学建模

由于每一个支撑臂都能够紧持对应的目标把手，每一个支撑臂都受到来自其对应把手上的一个力旋量fhk∈R6，因此，将所有支撑臂上的力旋量进行堆栈，广义力矢量fh可表达为

fh=col[fh1…fhk…fhK]，

(5)

式中：col为多个矢量的列矢量堆栈；fh∈R6K. 当多臂空间机器人对目标实施操作时，自由飘浮的多臂空间机器人运动学方程可表达为

(6)

式中：Hb、Hm、Hbm和H分别为机器人本体、手臂、本体手臂耦合和广义变量对应的惯量矩阵；q为机器人多臂关节空间变量；cb和cm分别为本体和手臂的非线性速度独立项；τθ、τ分别为所有手臂的控制扭矩和广义扭矩；Jh为广义变量qg映射到所有机械臂末端的雅克比矩阵，Jh的分块子矩阵Jhk对应第k条手臂，Jbk和Jmk分别对应第k条手臂和Σ0与该手臂关节空间q之间的雅克比映射，二者满足(7)式：

(7)

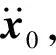
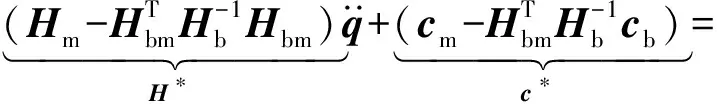
(8)

1.4 多臂操作约束

与单臂机器人不同，多臂空间机器人通过多条机械臂对同一个单刚体目标进行操作，多机械臂之间会构建出几个相互耦合的运动学闭链，这些支撑臂在笛卡尔空间的运动关系受到约束。图3所示为运动学闭链示意图，下面以4臂机器人为例描述约束运动学。

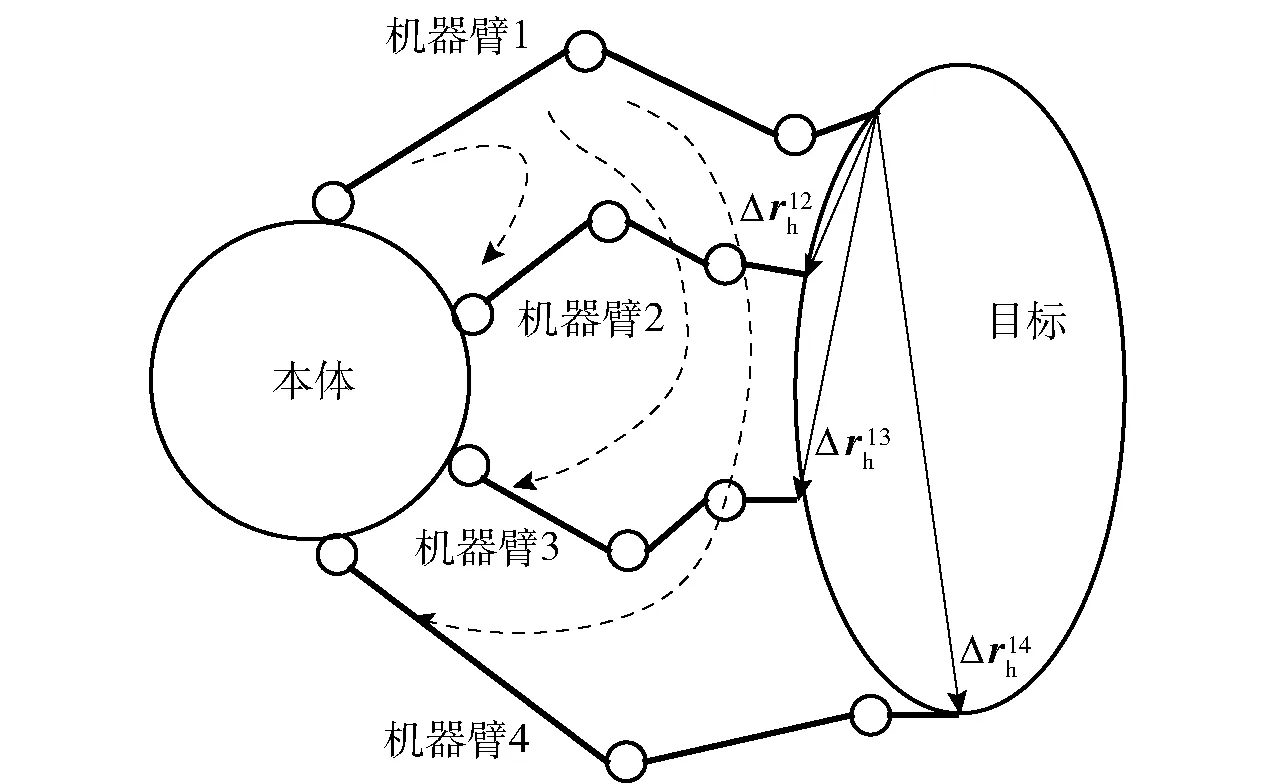
图3 多臂运动学约束及闭链示意图Fig.3 Multi-arm kinematics constraints and close-loop chains

设第k1条机械臂和第k2条机械臂之间在速度层面的运动学约束关系为

(9)

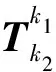
(10)

(11)

两个支撑手之间的位置矢量关系为

(12)

(13)

式中：E(q)∈Rnθ×nθ为约束雅克比矩阵，nθ为关节空间维度；子块矩阵

(14)

显而易见，在轨道微重力环境下多支撑臂之间的约束关系与空间机器人本体的运动无关，因此，在速度层面上关节坐标系下的运动学关系可描述为

(15)

2 全身接触柔顺策略

当机器人受到来自目标把手的较大拖拽力时，机器人为防止机械臂过应力，势必需要顺应该牵引力，从而控制机器人的运动。本文将机器人CoM构建为体现笛卡尔空间机械阻抗特性的弹簧、阻尼和惯量特性，并将每条机械臂独立控制为导纳特性，从而构建出一种组合柔顺策略。

2.1 CoM层面的全身阻抗控制

空间机器人的线动量和角动量可表达为

(16)

式中：线动量P0和角动量L0可以用机器人上配置的惯性器件(IMU)测量得出。另外，机器人关节空间和CoM间的运动学关系为

(17)

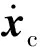
(18)

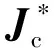
(19)

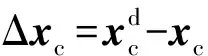
2.2 多臂力分配

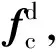
(20)

式中：fh=col[f1…fk…fK]为多支撑臂末端受到的广义力堆栈表达；W为抓捕矩阵，其子分块矩阵Wk可表达为

(21)

显然，多臂操作时抓捕矩阵W为冗余解，且不可逆，因此求解其Moore-Penrose伪逆[13]作为从CoM上的合力到多个支撑臂末端的分配矩阵W+，体现抓捕矩阵W最小二范数意义上的广义平均，分配关系满足：

fh=W+fc.

(22)

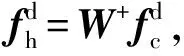
2.3 独立机械臂层面的导纳控制

(23)

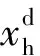
(24)

期望末端在Σc下加速度可表达为

(25)

3 基于QP框架的控制综合

本文采用多目标优化方法对机器人进行控制并在线生成运动行为，这种动态行为的控制需求与腿足机器人行走控制有一定的相似之处。Kuindersma[14]等将腿足机器移动问题抽象为QP问题并进行求解。Feng等[15]将Atlas仿人机器人的运动学和动力学分别抽象为QP问题，并将其应用到DARPA机器人挑战赛上。此外，其他学者也开展了类似研究工作[16-20]。

本节将多个控制目标构建成QP形式，并将运动方程构建成等式约束，然后考虑关节限位、关节速度和力矩限制并构建了不等式约束。

3.1 基于QP的控制综合

(26)

(27)

s.t.Ce=Cχ+c=0，

(28)

Ci=Dχ+d≥0，

(29)

式中：Ce和Ci分别表示等式约束和不等式约束；C、c、D和d为标准QP格式的约束矩阵；(27)式中的函数可以表示为如(30)式表述的二次函数：

0.5‖Aχ-b‖2，

(30)

G=ATA，

(31)

g=-ATb，

(32)

A和b由如下分块矩阵堆栈而成：

(33)

其中一组加权矩阵ωv(v=0,…,V)用来综合一系列控制行为目标。

3.2 全身柔顺控制的优化目标

为实现多臂空间机器人在多点接触过程中接触柔顺的目的，本节设计了全身柔顺优化目标Ec，通过惩罚与期望输入的偏离将柔顺目标纳入基于QP的多目标寻优体系。用优化变量χ整理(24)式，可得

(34)

通过惩罚期望笛卡尔空间加速度和实际CoM加速度，得到Ec表达式为

(35)

(36)

Ac、bc为全身柔顺控制优化目标Ec形如(2))式的不等式约束矩阵。由此可知，(36)式构建了期望运动和实际运动之间的负反馈控制率，从而建立了优化目标Ec的闭环。

3.3 关节力矩优化目标

作为接触控制最为重要的目标之一，接触臂关节力矩应该尽可能小，因此应惩罚期望的关节力矩和当前力矩之间的偏离。期望力矩可以设置为0，从而达到力矩广义最小的目的，同时功率消耗也最优。所有支撑臂对应关节力矩与期望0力矩之间的偏离关系可表达为

(37)

式中：Aτ、bτ为关节力矩优化目标Eτ形如(27)式的不等式约束矩阵。Ec和Eτ可通过(33)式形式堆栈处理，转化成形如(27)式所示的新的动态优化控制目标。

3.4 约束条件

3.4.1 等式约束

空间机器人的运动方程可以用来定义QP问题的等式约束，整理(8)式可得出等式约束表达式为

(38)

式中：C1、c1为机器人系统遵循动力学模型的等式约束矩阵；Ce1为遵循动力学模型约束形如(28)式的表达式。当支撑臂数量大于1时，支撑臂之间的运动受到约束运动方程的限制，根据(15)式，支撑臂运动学约束关系可表示为

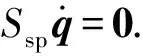
(39)

将(39)式按照优化变量重新整理，可得

(40)

式中：C2和c2为机器人系统遵循多臂协作运动约束的等式约束矩阵；Ce2为遵循多臂运动约束形如(28)式的表达式。将(38)式和(40)式进行堆栈处理，可得到(28)式中QP问题的等式约束Ce(χ)：

(41)

式中：C和c分别为遵循动力学模型和多臂运动约束的堆栈表达；总的等式约束Ce用来表达Ce1和Ce2的堆栈组合。

3.4.2 不等式约束

(42)

依据优化变量χ，将(42)式整理为如下不等式约束：

Dq1χ+dq1≥0，

(43)

Dq2χ+dq2≥0，

(44)

Dqd1χ+dqd1≥0，

(45)

Dqd2χ+dqd2≥0，

(46)

同理，考虑关节力矩约束，可得约束形式为

Dτ1χ+dτ1≥0，

(47)

Dτ2χ+dτ2≥0，

(48)

式中：Dτ1=[I00]；Dτ2=[-I00]；dτ1=τmax；dτ2=τmax. 将(43)式、(45)式和(47)式进行堆栈整理，可得(29)式中不等式约束Ci(χ)的统一表达式：

Ci(χ)=Dχ+d≥0，

(49)

式中：系数阵D=col[Dq1,Dq2,Dqd1,Dqd2,Dτ1,Dτ2]，d=col[eq1,eq2,eqd1,eqd2,eτ1,eτ2]分别为机器人系统形如(29)式的不等式约束对应的约束矩阵。

3.5 基于二次规划的控制综合和求解

当得到如(27)式所示的动态优化控制目标以及如(28)式和(29)式所示的约束条件后，多臂空间机器人操作大型目标问题已经转化为一个标准QP问题，本文采用CVX优化求解器[21]对该多目标优化问题求解。

4 仿真与实验

机器人操作策略及控制器分别通过仿真和降维度实验的方式进行验证。首先，通过建立4臂机器人仿真模型构建近似轨道的微重力环境，并对惯性系进行简化；其次，开展基于气浮的物理实验。由于在地面重力环境下构建微重力的局限性，本实验采用气浮技术构建水平面内的3自由度微重力环境，包含2个平动和1个转动自由度。虽然该方法无法直接验证全维度算法，但能够局部验证包含有限维度微重力特性算法的有效性。物理实验可作为仿真验证的补充，通过降维度实验和全维度仿真共同验证柔顺策略的有效性。

4.1 仿真及分析

大型目标采用圆柱体来模拟火箭末级，并给出特定的初始三轴角速度来模拟目标翻滚。机器人以恒定速度向期望操作点靠近，达到操作点附近时多条臂开始对目标表面的把手实施操作，从而产生接触碰撞。全身控制器在该顺次过程中对机器人进行在线运动规划与控制，以驱动机器人有效地应对接触过程。

图4所示为6自由度空间机械臂自由度配置和关节坐标系定义示意图。

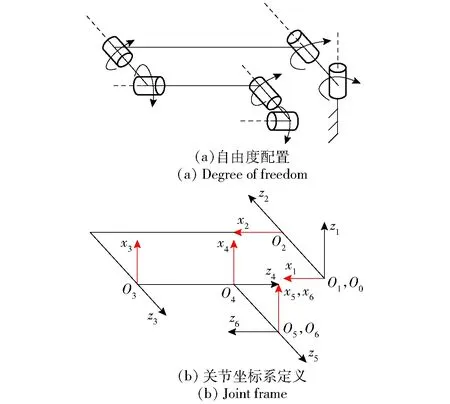
图4 机械臂连杆模型Fig.4 Arm configuration model

CoM和目标一个把手的运动轨迹如图5所示。由图5可见，目标与机器人的质量比为4.82，大型目标在接触过程中占据绝对的主动权。

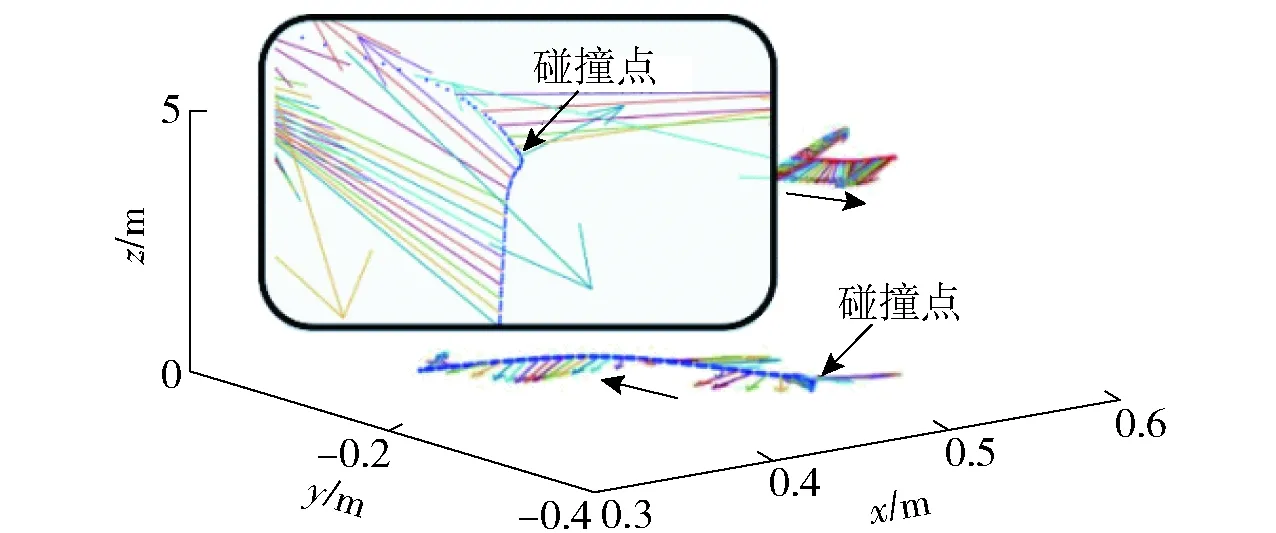
图5 CoM和目标某把手的运动轨迹Fig.5 Trajectories of CoM of chaser and one target’s handle

如图6所示为4条机械臂关节力矩，从图6(a)到图6(d)依次为顺次接触的4条机械臂，每个子图中包含本条机械臂的j1、j2、j3、j4、j5、j66个关节力矩，虚线表示本臂与把手碰撞时刻示意。从图6中可见，在机械臂1和机械臂2作为支撑臂的柔顺接触控制下，本体和目标间的相对运动速度得到了有效控制。

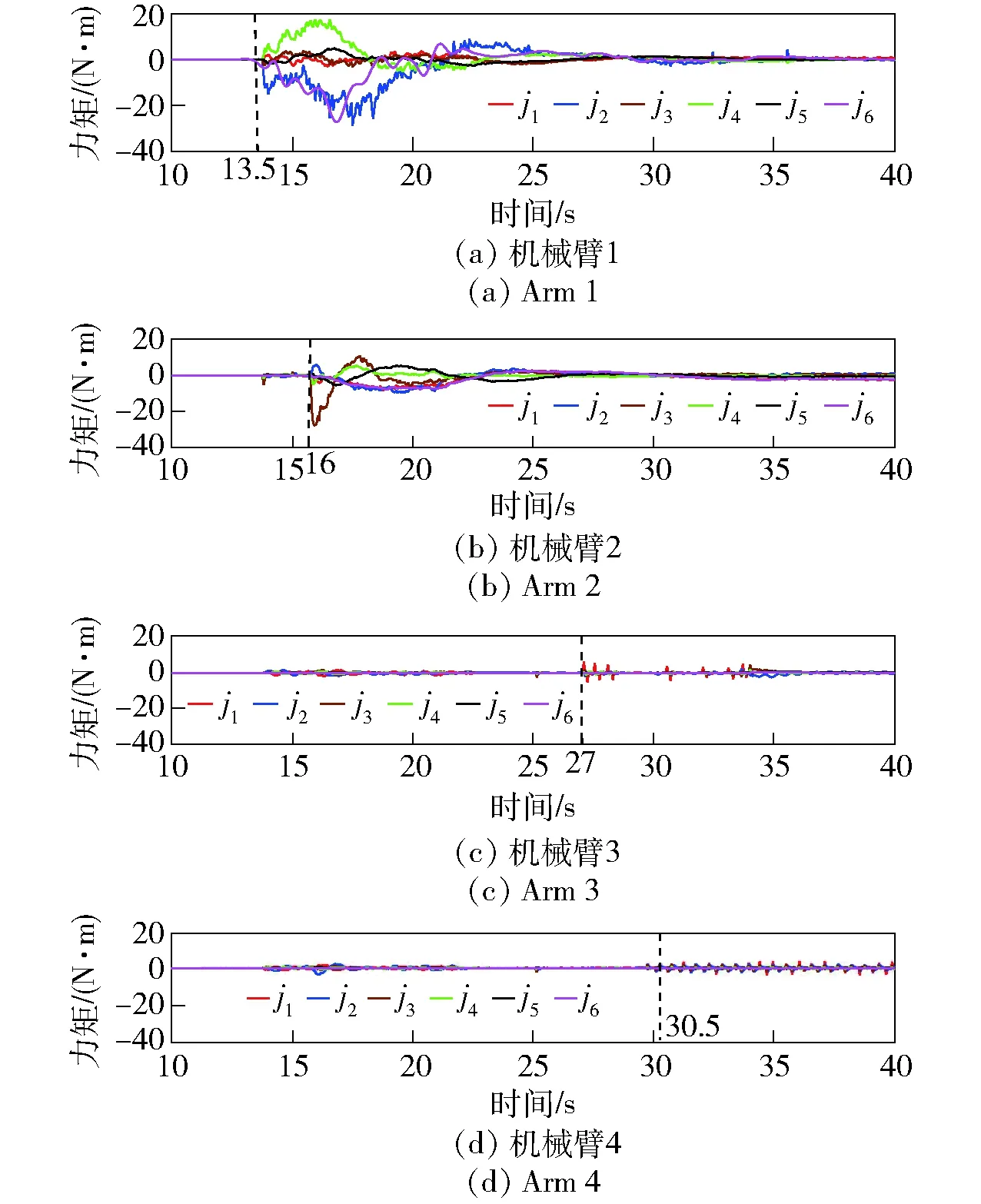
图6 4条机械臂关节力矩曲线Fig.6 Joint torque curves of four arms

如图7所示为机械臂末端受力情况，图7(a)、图7(b)分别表示fa1、fa2、fa3、fa4和ta1、ta2、ta3、ta44条机械臂末端的力、力矩的模，不包含方向信息，因此所有数据均为正。与关节受力情况类似，机械臂1和机械臂2承担了几乎所有的接触柔顺任务，为后续接触臂提供了良好的接触环境。

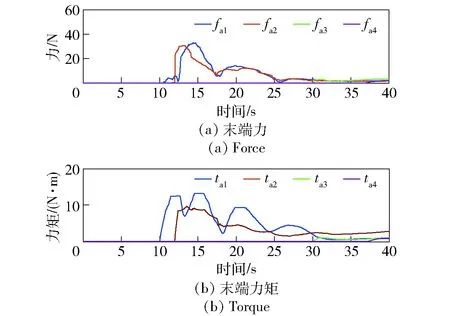
图7 4条机械臂末端力和力矩的模Fig.7 Forces and torques at the terminals of four arms

如图8所示为机器人操作目标仿真过程截图，结合图5、图6和图7中各个指标的变化趋势分析可知，在多点接触过程中，机器人能够以柔顺的接触行为应对来自大型目标的拖拽，尽可能柔顺关节力矩，防止损坏或任务失败。综合上述数据可知，CoM 轨迹柔顺、受力曲线有界且过度平滑，接触过程柔顺可控，证明了相关算法的有效性。

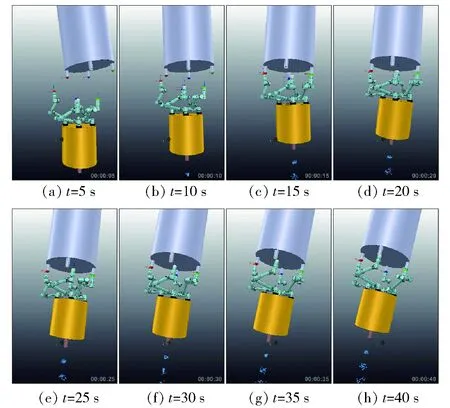
图8 机器人操作大型目标仿真截图Fig.8 Screenshots of robot capturing target in simulation

4.2 实验及分析

在地面重力环境下构建轨道微重力环境极具挑战性，因此本文将多臂系统简化成水平面内的降维度双臂系统，作为仿真验证的补充，以验证本文提出方法的有效性。从控制角度而言，双臂降维度系统在运动方程上要比4臂全维度系统的复杂度低，对比4臂仿真模型和双臂实验模型可以发现，实验系统的3自由度机械臂在3自由度气浮降维度空间内为非冗余构型，仿真系统的6自由度机械臂在6自由度工作空间中也是非冗余构型，二者的算法设计与计算流程严格一致，在某种意义上，降维度系统及其计算过程是全维度系统的“子集”。因此，从实验验证角度而言，降维度系统能够覆盖验证全维度系统关于“在轨微重力特性”相关算法的有效性，这也是本文提出的降维度实验方法的理论依据。

图9所示为基于气浮实验的双臂实验平台，其中右臂和左臂分别为支撑和摆动臂。实验过程中，实验员对右臂施加拖拽力并模拟外界目标施加给机器人的力。当机器人被实验员拖拽产生运动时，机器人右臂作为支撑臂与“目标”连接，并应对外部环境拖拽力，从而产生柔顺控制行为。

图9 双臂地面实验平台Fig.9 Ground experimental platform of dual-arm robot

图10和图11分别为接触柔顺实验过程中双臂jr2、jr3、jr5和jl2、jl3、jl5关节运动曲线和支撑臂腕部力Fx、Fy与力矩Tz传感器曲线。由图10和图11可见，所有参数能够在柔顺控制器控制下保持较低的系统刚度，且有界可控。

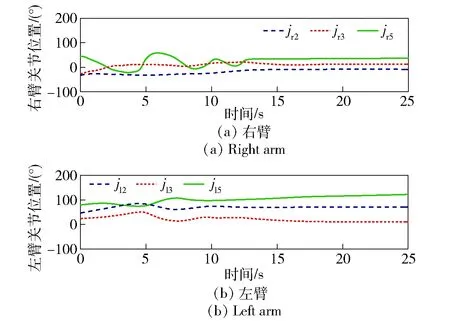
图10 双臂的关节位置Fig.10 Joint positions of two arms

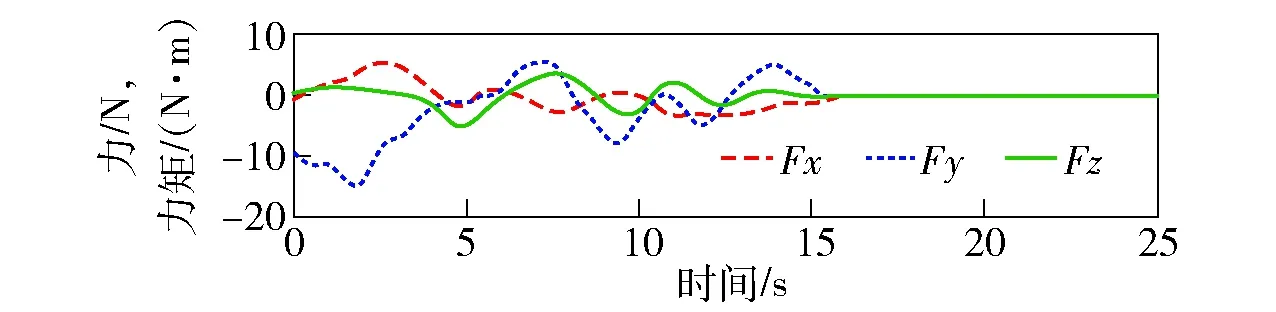
图11 支撑臂腕部力与力矩Fig.11 Force and torque in the wrist of supporting arm

图12所示为气浮实验的视频截图，在实验人员拖拽下机器人通过右臂构建笛卡尔空间的柔顺特性，从而实现接触柔顺的目标。从图10、图11和图12中可以看出，机器人在受到外部环境拖拽力情况下，能够有效制定应激运动行为，并保障与环境间的接触柔顺，从而验证了组合式全身接触柔顺控制策略和基于QP方法的有效性。

5 结论

本文提出了一种组合式全身柔顺控制方法，解决了多臂空间机器人捕获大型翻滚目标时的柔顺接触及碰撞安全问题。本文主要结论如下：

1)提出了一种组合式柔顺控制策略，分别设置CoM的阻抗行为和支撑臂独立的导纳行为，兼顾了全身运动行为和多臂力分配的目标。

2) 提出了一种基于QP的多目标优化控制框架，将全身柔顺控制和关节力矩等优化目标统一起来，并具有一定的扩展性，可管理不同维度的优化目标。

3)将上述接触柔顺控制方法通过基于气浮的实验系统进行验证，实验结果证明了该方法的有效性。

后续将持续开展多臂捕获接触柔顺研究，考虑如何将动态力分配过程纳入柔顺控制范畴，从而进一步增强接触柔顺性。