城镇客车车身振动特性仿真分析

王建美，冯 理 Wang Jianmei，Feng Li



城镇客车车身振动特性仿真分析

王建美，冯 理 Wang Jianmei，Feng Li

（武汉华夏理工学院 汽车工程学院，湖北 武汉 430223）

以一款城镇客车为研究对象，针对其车身壁板振动剧烈的问题，利用有限元法对其结构振动进行相关研究。对车身进行模态计算和谐响应分析，得到车身结构的固有频率、模态振型和位移响应；结果表明：车身顶棚的振动比较剧烈，尤其在75 Hz时振动位移量最大，车身前部和两侧也有明显的振动形变；最后，提出降低振动、提高乘坐舒适性的措施。

NVH；模态分析；谐响应分析

0 引 言*

随着人们对汽车安全性和乘坐舒适性关注度的提高，汽车振动的控制水平已逐渐成为衡量汽车质量的重要指标之一。各汽车企业在对新车型的开发和设计上，也更加注重汽车NVH（Noise、Vibration、Harshness，噪声、振动、声振粗糙度）特性的研究[1]。发动机运转、传动系统和悬架系统振动以及路面不平度等引发的汽车振动易使驾驶员和乘客感到疲劳不适，甚至诱发交通事故[2]。客车的承载结构主要集中于车身结构，其使用寿命及乘坐舒适性直接受车身结构刚度和振动特性的影响；因此，对其研究具有一定的现实意义。

1 车身几何模型的建立

以一款5 995 mm×2 180 mm×2 750 mm半承载式城镇客车为研究对象，利用几何建模软件CATIA，根据车身各部分的尺寸数据建立车身三维几何模型。由于车身结构较为复杂，其中包含非承载结构以及对结构变形、应力影响不大的非主要承载件等，所以根据车身结构的实际受力状态，对模型进行抽象和简化。在不影响整车结构刚度、强度的基础上大幅提高建模以及后续分析的速度。

在建立几何模型过程中，结合该城镇客车的车身结构特点，把车身板块拆分为顶棚、底架、左右侧围、前围、后围及地板6个板块分别进行建模，将建立好的各个部分在CATIA中进行装配，最终得到车身结构模型如图1所示。

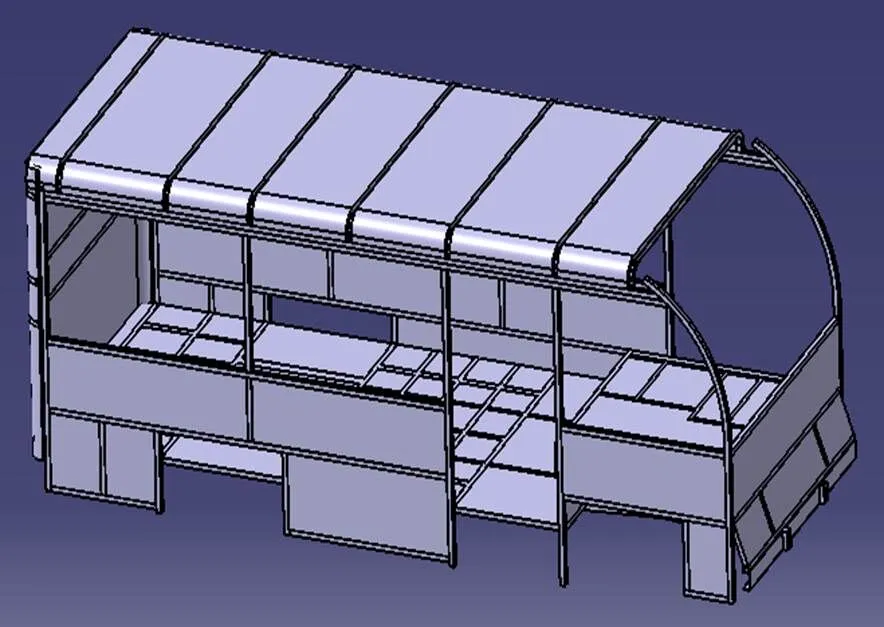
图1 城镇客车车身几何模型

2 车身有限元模型的建立

2.1 材料属性的指定

几何模型建好后指定其材料属性。材料属性参数有泊松比、密度、剪切模量、弹性模量及屈服极限等，客车车身结构材料有两种，Q235钢和16 Mn钢，16 Mn钢用于底架部分，Q235钢则用于前后围、侧围、底板和顶棚部分。材料参数见表1。

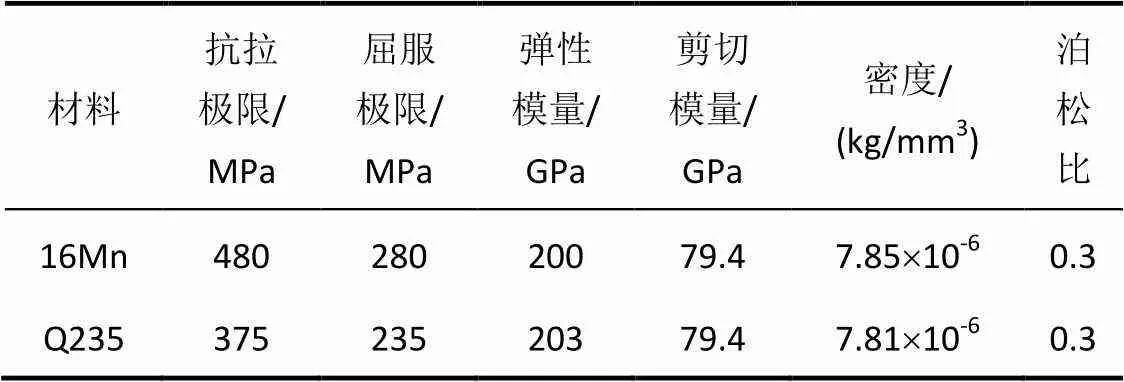
表1 材料参数

2.2 车身有限元模型的生成

利用LMS Virtual.Lab对城镇客车车身结构进行网格划分，生成车身结构有限元模型如图2所示。模型中网格单元总数是49 201，节点数量是57 292。

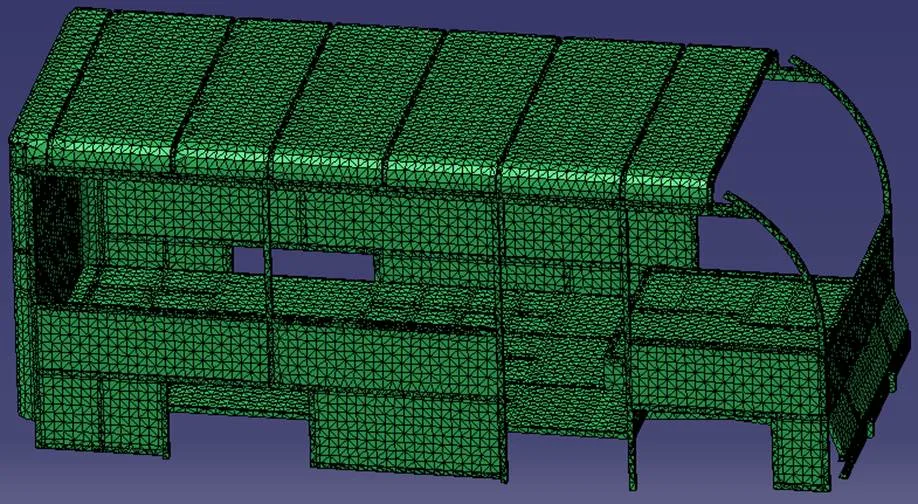
图2 车身结构有限元模型

3 客车车身结构模态分析

3.1 模态分析的基础理论

模态分析是一种计算分析结构动力特性的方法，用于结构在自由振动状态下的分析，也是动力学分析的前提，通过模态计算可以清楚认识系统结构的振动特性，得到结构的固有频率和相应振型[3]。由于大多数机械结构都要求避免共振，所以模态分析在动力学分析中起着重要作用。考虑结构的自由模态，在没有受到阻尼和外力的作用时，系统振动属于自由振动，振动方程为

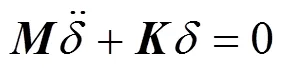
在系统自由振动的模式下，各个节点作简谐运动，振动位移为

式中：0为固有振型；为固有频率；为振动时间；为相位角。

将式（2）代入式（1）得

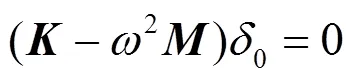
因为各节点的振幅0不全部为零，因此，式（3）所包含的矩阵行列式必须等于零，这时结构系统的固有频率方程可以写为

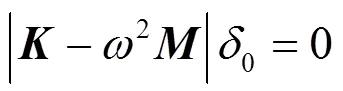
需要说明的是，结构模态是实数模态。

3.2 模态分析评价原则

车身结构的振动性能主要从两方面进行评价：

（1）车身结构的低阶频率（主要指1阶扭转和弯曲）要避开客车发动机怠速频率和客车悬架的固有频率，避免结构发生共振；

（2）车身结构固有频率不应该出现在人体敏感的振动频率段。

3.3 模态结果分析

客车车身的模态分析一般是在车身结构无阻尼自由振动条件下计算，模态分析主要是计算车身结构的固有频率和振型，由于车身动力性能受其高阶频率的作用很小，因此对于高阶频率不做计算。在LMS Virtual.Lab中计算车身结构前20阶模态频率和振型，根据模态计算的结果，取客车车身前6阶模态参数见表2，前6阶模态振型如图3所示。

表2 客车车身前6阶振型

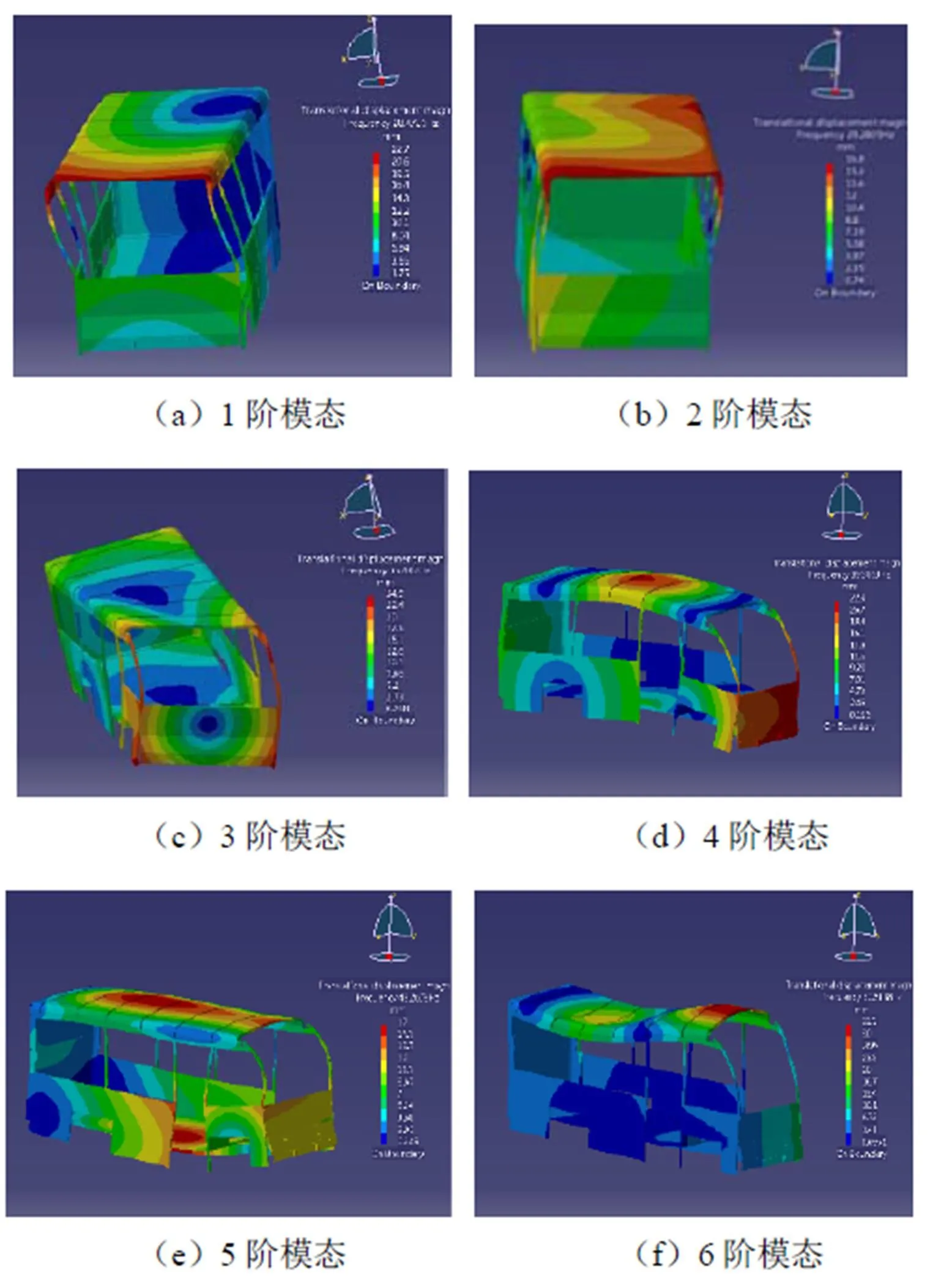
图3 前6阶车身结构模态振型

由结构模态振型可以看出，每一阶模态振型中顶棚都表现出局部振动。1阶模态频率为28.47 Hz，表现为顶棚的摆动，车身整体振幅较大，顶棚由后至前振动依次增强；2阶模态频率为29.28 Hz，仍表现为顶棚的摆动，相对于1阶模态来说整体振幅较小；3阶模态频率为35.48 Hz，整体模态表现为1阶扭转变形，车身前半部分振动较强烈；4阶模态频率为39.39 Hz，表现为整体弯曲变形，前围和车顶棚中部变形较大；5阶模态频率为48.26 Hz，表现为车身的弯曲变形，顶棚和底板部分变形最为明显；6阶模态振幅有所减小，频率为60.51 Hz，表现为车顶棚局部弯曲变形，尤其是驾驶员上方顶棚位置变形尤为强烈，振幅较大。综上，车身顶棚的变形比较明显，说明其刚度比较差，在外界力的作用下易发生振动变形。顶棚刚度差可能是因为车顶棚横梁或纵梁数量太少或钢板厚度不足，导致在汽车行驶过程中发生较大的振动变形。

通常情况下，汽车振动的最大激励源来自于发动机的振动和路面对轮胎的冲击力，尤其在发动机怠速运行时，最容易引起汽车整车共振；因此，在进行汽车设计时，结构模态的固有频率应避开发动机怠速时的激励频率。该型客车相关车身技术参数为：车身和悬架的共振频率为2.0～3.4 Hz，发动机怠速频率约为32 Hz，由模态结果可知，该车车身结构固有频率与发动机怠速频率不相同且不在车身和悬架的频率范围内，同时，路面激励通常情况下小于20 Hz；因此，理论上可以避免整个客车发生共振。

4 客车车身谐响应分析

谐响应分析主要是计算一种稳态响应，即线性结构受到随时间做正弦规律变化的载荷的稳态响应，可以得到在一定频率段下的位移响应曲线，进而获得峰值响应及其所对应的频率等。

发动机是汽车振动的重要激励源，在车身模态结果的基础上进行谐响应分析，其结果可以为车身结构的减振以及整车设计改进提供依据。

4.1 发动机激励力的确定

由于试验条件限制，发动机激励力很难准确得到，因此计算时所用激励力用单位简谐力代替。力的作用点选择发动机悬置的左右两点，力的方向选择左右相反来平衡力矩[4]。

对于4缸直列式发动机，其一个工作周期内产生两次惯性不平衡力。因而惯性力的频率可表示为

式中：为惯性力的频率，Hz；为发动机转速，r/min。

发动机正常工作时其转速范围是800～3 600 r/min，与其对应的2阶惯性力的频率范围是26.7～120.0 Hz，所以进行谐响应计算时力的频率范围选择为0～200 Hz。

4.2 边界条件的设定

为了消除刚体运动，获得准确的位移解，进行谐响应分析时要进行约束设置，但若施加的边界约束条件太多，则可能会出现不存在的附加约束力，进而影响计算结果。经综合考虑，车身的约束条件见表3。

表3 车身约束条件

注：U为横向自由度；U为纵向自由度；U为垂直自由度。

4.3 车身结构谐响应计算结果分析

经计算得到车身各处谐波振动响应。选取车身上7个点查看结果，7个观测点的具体位置见表4。

表4 响应点位置

计算得到各关键点的振动响应结果如图4所示。

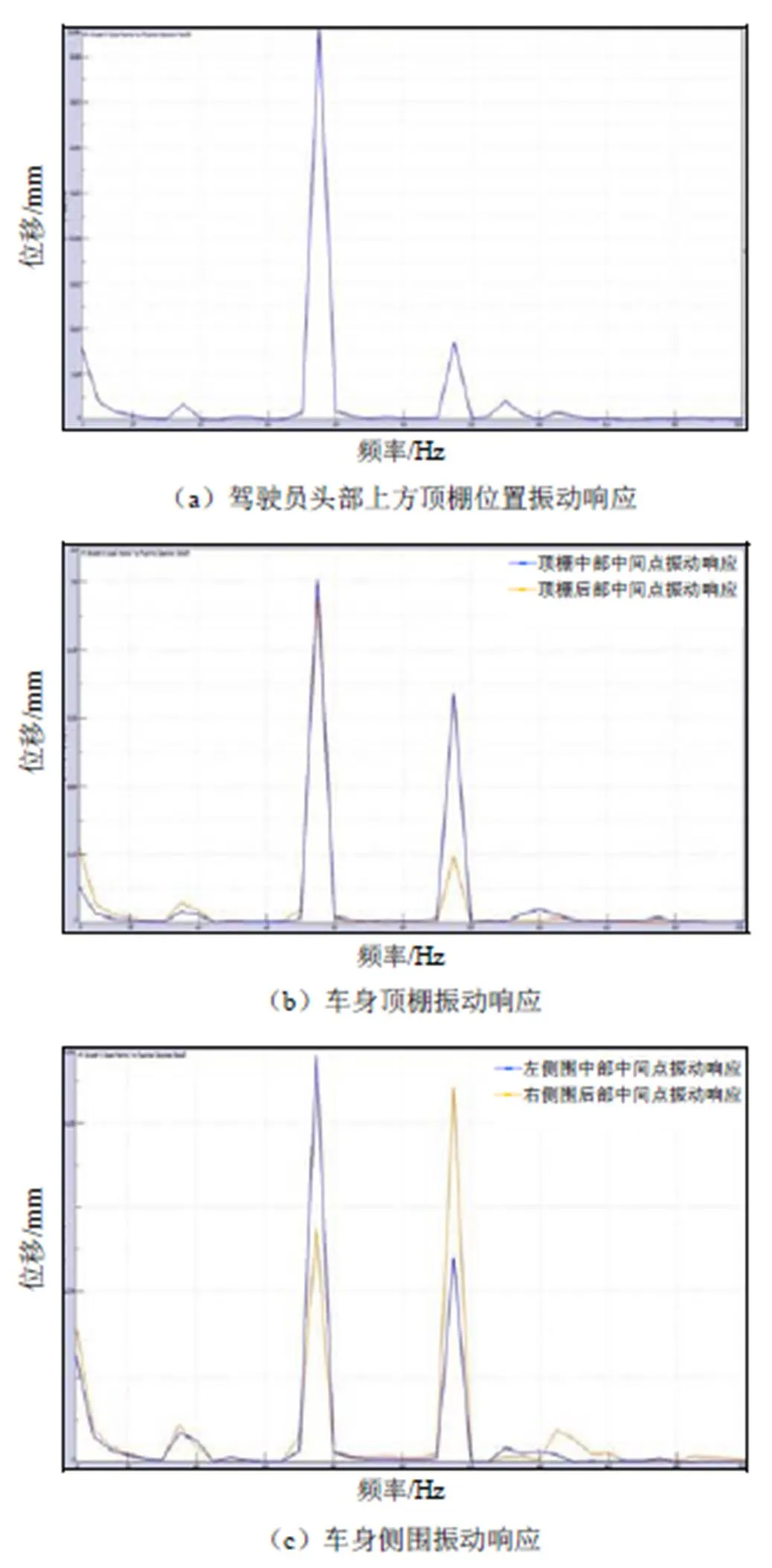
由以上结果可知：驾驶员上方顶棚的最大振动峰值出现在75 Hz附近，振动位移约为0.086 mm；车身顶棚的振动峰值主要出现在75 Hz和115 Hz附近，在75 Hz附近达到最大振动位移约为0.101 mm；车身两侧的振动峰值主要出现在75 Hz和115 Hz附近，在75 Hz附近达到最大位移量约为0.06 mm；车身底板中部处的振动峰值主要出现在5 Hz和70 Hz附近，在5 Hz附近达到振动位移最大约为0.009 mm，在底板后部的振动峰值主要出现在75 Hz附近，最大位移量约为0.005 mm。

综上可得，车身顶棚的振动位移量最大，其次是车身两侧，客车底板的振动位移量最小。车身顶棚（包括驾驶员上方顶棚部分）振动剧烈，会给车内带来辐射噪声，壁板两侧和底板的振动也会增加车内噪声，要降低车顶棚及侧面的振动，需要加大其刚度。可以增加车身顶棚及两侧的蒙皮钢板厚度，也可增加车顶及侧面横梁和加强筋的数量，通过加大零件的厚度或更换为强度更高的钢材来减小振动。

从频率来看，车身顶棚和两侧壁板振动峰值均出现在75 Hz和115 Hz附近，车身底板位移峰值所对应的频率也出现在75 Hz附近，此频率所对应的发动机转速在2 250 r/min附近；因此，为了降低车身壁板的振动，驾驶员应尽量避免使发动机长时间工作在2 250 r/min转速附近。

5 总 结

以一款城镇客车为研究对象，建立客车车身结构有限元模型，并对其进行模态计算和谐响应分析，得到车身结构的固有频率和振型以及振动响应结果。经分析可知，车身顶棚、两侧和车身前部的振动变形大，尤其是顶棚，刚度较差。车身壁板在75 Hz等频率时振动响应比较剧烈，所以驾驶员应尽量避免使发动机长时间工作在此频率所对应的2 250 r/min转速附近。

[1]陈龑，林建平，胡小舟，等. 基于模态分析的某客车车身NVH性能优化[J]. 现代制造工程，2013（6）：51-54.

[2]付长虎. 客车车身振动和声学特性的仿真及改进研究[D]. 镇江：江苏大学，2013.

[3]束元，周毅，周鋐. 基于模态分析的某客车白车身结构改进[J]. 佳木斯大学学报（自然科学版），2012（5）：687-690.

[4]胡强，张健，胡朝辉. 基于典型工况的发动机悬置优化设计[J]. 企业科技与发展，2013（17）：12-14.

湖北省教育厅科学研究计划指导性项目（B2017395）；武汉华夏理工学院校级科研基金项目（16023）。

1002-4581（2019）01-0011-05

U463.82

A

10.14175/j.issn.1002-4581.2019.01.004

2018−09−25