谷值电流控制的H桥逆变器的非线性现象

吴荣华，江 伟

(东华理工大学 江西省新能源工艺与装备工程技术研究中心，江西 南昌 330013)

电力电子电路是一种典型的非线性系统，表现出相当复杂的非线性动力学行为，如次谐波振荡、周期跳跃、各种类型的分岔及混沌现象[1-5].逆变器是一种基本的电力电子电路，在工程中会发生一些不稳定现象，如运行状况突变、刺耳电磁噪声、系统突然崩溃等[6].因而，对逆变器中的非线性现象进行研究有重要的意义.

近年来，对逆变器非线性现象的研究已开展，文献[7]研究了H桥逆变器在比例控制下的非线性现象；文献[8]深入分析了H桥直流斩波变换器边界碰撞分岔的机理；文献[9]应用频闪映射图、迭代图、分岔图分析了工作在比例调节下的逆变器出现的非线性现象；文献[10]研究了逆变电路在数字控制下发生振荡的内在机理；文献[11]运用斜坡补偿的方法，控制了单相SPWM逆变器的快标分岔.

目前，对H桥逆变器的非线性研究，主要针对正弦脉宽控制，对于谷值电流控制的H桥逆变器的非线性现象研究未见报道.谷值电流控制属于电流控制的一种，兴起于20世纪60年代后期，其暂态闭环响应快，具有简单自动的磁通平衡功能[12].因此，笔者以谷值电流控制的H桥逆变器为研究对象，分析其工作原理，建立离散模型，采用频闪图、折叠图、分岔图和Lyapunov指数谱等方法，研究非线性动力学行为的演变过程，运用Jaconbian矩阵法分析系统的稳定性，为该逆变器的合理设计提供指导.

1 谷值电流控制的H桥逆变器的工作原理及离散模型

谷值电流控制的H桥逆变器的工作原理如图1所示，其主电路由直流电压源E、开关管VT1～ VT4、感性负载R及L构成.采用电流反馈控制，将参考电流iref和负载电流i的比较结果送入RS触发器的S端，比较结果信号与R端的时钟脉冲信号一起控制开关管的导通与截止.在每个周期的开始，时钟脉冲给出的触发信号使RS触发器输出低电平，开关管VT1，VT3截止，VT2，VT4导通，逆变器工作在状态1，负载电流下降；当i下降至iref时，RS触发器置位，输出高电平，开关管VT1，VT3导通，VT2，VT4截止，逆变器工作在状态2，负载电流开始上升，等待下一个时钟脉冲的到来，如此循环往复.

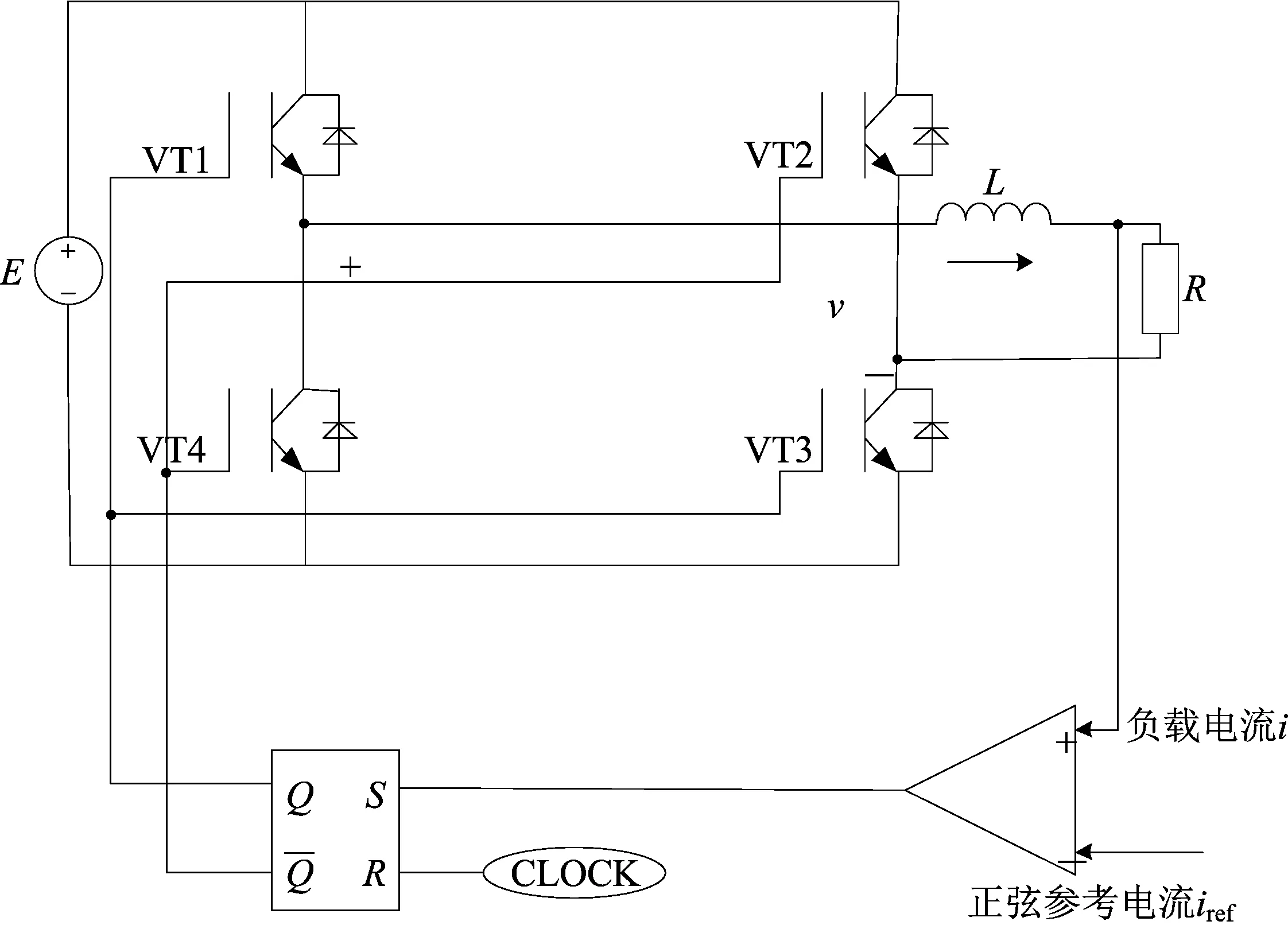
图1 谷值电流控制的H桥逆变器的工作原理图

开关管VT1，VT2，VT3，VT4以互补的方式工作，逆变器有2种工作状态.状态1的状态方程为

(1)

状态2的状态方程为

(2)

图2为负载电流波形.由图2可知，在RS触发器的控制下，系统在两种状态之间转换，TS=1/fS是触发器开关的时钟周期，在第n个时钟脉冲周期内，TS-tn表示状态1时间，tn表示状态2时间.参考电流iref=Isin(2πft)，且fS≫f，因此，iref在每个开关周期TS内可近似看作常量.

图2 负载电流波形

对式(2)积分可得第n个时钟周期状态2的占空比为

(3)

其中：α=E/R，β=(R×TS)/L，in为负载电流i在采样时刻nTS的值.

频闪映射理论建模的核心为：选择一个迭代初值，利用状态方程求解下一周期的解，如此循环往复，最终得到用第n个开关周期状态变量表示第n+1个开关周期状态变量的表达式[13].由式(1)～(3)导出的电路离散模型为

in+1=(iref-α)e-β(1-Dn)+α，

(4)

其中：in+1为负载电流i在采样时刻(n+1)TS的值.

2 谷值电流控制的H桥逆变器的非线性分析

采用频闪采样图、分岔图、折叠图和Lyapunov指数谱等方法，分析逆变器的非线性现象.取控制器的开关频率fS=10 kHz，参考电流iref的幅值I=1 A，频率f=50 Hz，则iref=sin(100 πt).电路的其他参数为：R=10 Ω，L=10 mH，直流电压为1～40 V.

2.1 频闪采样图

频闪采样图能快速反映系统的稳定性，其绘制方法如下：基于式(4)的离散模型，对迭代稳定后的状态变量在开关周期TS=0.1 ms下采样并保存采样值，得到不同输入电压下的频闪采样图，如图3所示.由图3(a)可知，当E=10 V时，逆变器的频闪图存在杂乱的采样点，说明此时系统的状态是混沌的；由图3(b)可知，当E=35 V时，频闪图是一条单值线，说明此时系统的状态是稳定的.

(a)：E=10 V; (b)：E=35 V.图3 不同输入电压下的频闪采样图

2.2 分岔图

分岔图是研究系统复杂动力学行为的有效途径，它不仅能描绘出系统由稳定向混沌的演变，还能得到系统稳定与不稳定的临界点.以上述的频闪图为基础，取输入电压E为可变量，其他参数固定不变，对50个正弦周期的[(3/2)π,2π]区域采样绘制系统的分岔图，可得负载电流i随输入电压变化的分岔图(见图4).由图4可知，在输入电压E从1 V增大至40 V的过程中，系统由混沌状态突然向稳定的周期运动状态转变：当E<19 V时，采样结果密集分布在一定区域内，说明系统处于混沌状态；当E>19 V时，每次的采样结果都重叠，形成一条单直线，表明系统突变进入稳定状态，该结论与图3的一致.

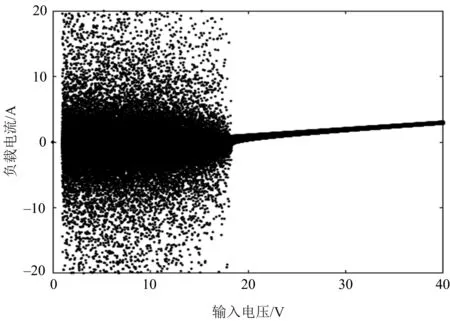
图4 负载电流i随输入电压变化的分岔图

2.3 折叠图

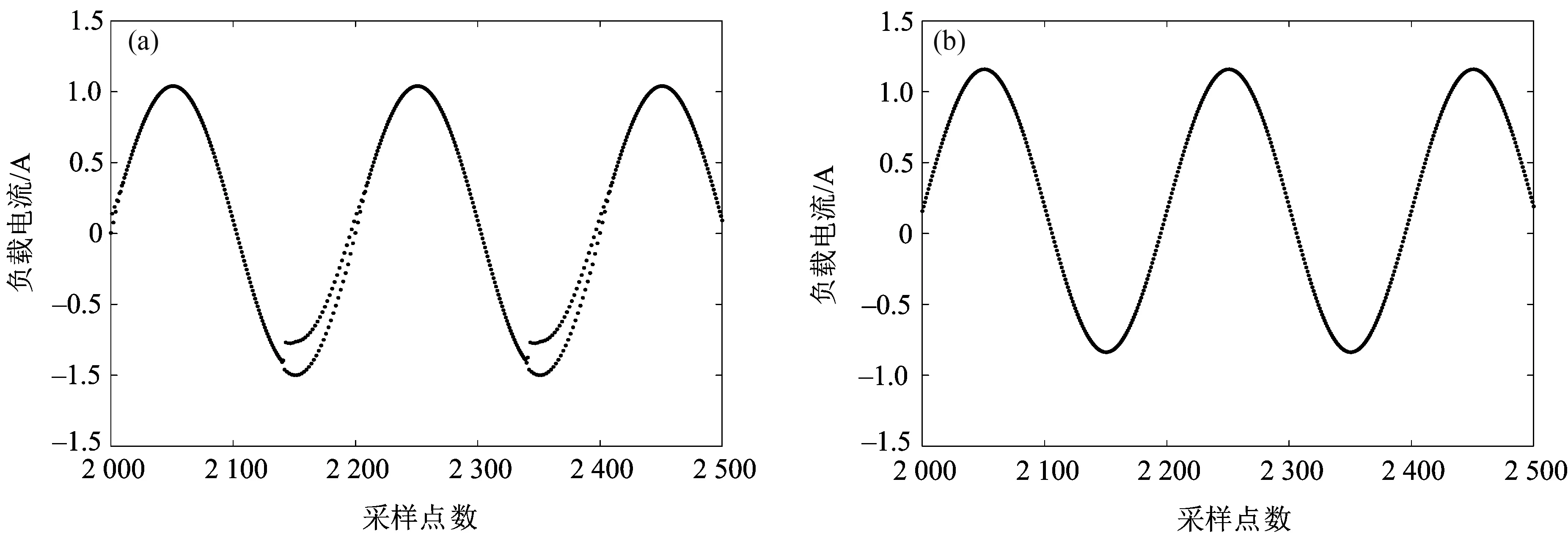
折叠图能直观反映出系统的非线性现象，其绘制方法如下：选取初值代入系统的离散方程进行迭代，对每个正弦周期采样M个点(M=fS/f=200)，将稳定后的数个正弦周期按采样时刻对齐后折叠[14].图5为系统在不同输入电压下的折叠图.由图5(a)可知，当E=10 V时，折叠图中部分采样点杂乱无章，表明此时系统处于混沌状态；由图5(b)可知，当E=35 V时，每个采样点均重叠，形成一条稳定、光滑的正弦曲线，表明此时系统处于稳定状态.折叠图的分析结论与图4的一致.折叠图更形象刻画了不同输入电压下系统的非线性动力学行为.

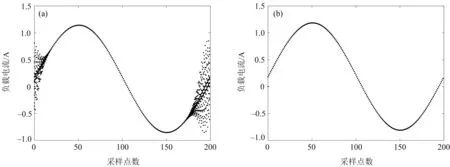
(a)：E=10 V; (b)：E=35 V.图5 不同输入电压下的折叠图

2.4 Lyapunov指数谱

Lyapunov指数是一种定量描述系统运动的特征量，能有效判定系统分岔点的位置.根据Lyapunov指数的定义，对于1维映射xn+1=f(xn)，其Lyapunov指数为

(5)

当LE<0时，系统处于稳定状态；当LE>0时，系统处于不稳定状态；LE=0对应系统稳定与不稳定的分界点，即分岔点.

根据上述对1维映射的Lyapunov指数定义，由式(4)可得谷值电流控制的H桥逆变器的Lyapunov指数为

(6)

令输入电压E由1 V变化到40 V，步长为0.05 V，在每个输入电压E值下迭代100次，绘制负载电流i随输入电压变化的Lyapunov指数谱(见图6).由图6可知，当E<19 V时，Lyapunov指数都大于零，系统处于混沌状态；在E≈19 V处，Lyapunov指数曲线过零点，可知此位置是系统由混沌进入稳定的临界点；此后，Lyapunov指数总是小于零，系统处于稳定状态.

图6 负载电流i随输入电压变化的Lyapunov指数谱

2.5 不同输入电压对系统稳定性的影响

为了分析不同输入电压对系统稳定运行范围的影响，取输入电压E为变量，绘制出负载电流i随负载电阻R和电感L变化的分岔图(二者分别见图7，8).由图7～8可知，当E=10 V时，系统状态由稳定迅速向混沌转变；当E=35 V时，负载电流i随电阻R变化的分岔图稳定运行的范围比E=10 V时的大；E=35 V时的负载电流i随电感L变化的分岔图一直是稳定的，该结论与图4的一致.

(a)：E=10 V; (b)：E=35 V.图7 不同电压下负载电流i随电阻变化的分岔图

(a)：E=10 V; (b)：E=35 V.图8 不同电压下负载电流i随电感变化的分岔图

3 谷值电流控制的H桥逆变器的稳定性分析

对离散迭代模型xn+1=f(xn,dn)(其中xn为第n次迭代值，xn+1为第n+1次迭代值)，基于Jacobian矩阵定义，可得

(7)

其中：XQ，DQ为系统的稳态解.

在谷值电流控制的H桥逆变器中，参考电流值iref在每个TS均发生变动，因此无法对每个开关周期进行Jacobian矩阵稳定分析，但该文的参考电流值iref是在每个周期的固定时刻采样的，可认为是恒定的，因而取iref为控制参数，可知in+1=f(in,iref)，in+1=in是逆变器的稳定点.

由Jacobian矩阵定理可得

(8)

其中：λmax为Jacobian矩阵最大模特征值.当|λmax|<1时，系统是稳定的；当|λmax|>1时，系统是不稳定的；|λmax|=1是系统稳定与不稳定的临界点.

将式(3)代入式(4)，可得

(9)

由式(9)可得系统的不动点为

(10)

将式(9)～(10)代入式(8)，可得

(11)

根据式(11)，取E=19 V，λmax=-1，其他参数保持不变，可得iref=0.142 A.保持iref=0.142 A不变，取E=10 V，可得|λmax|=1.204>1，可知此时系统是不稳定的.取E=35 V，可得|λmax|=0.981 3<1，可知此时系统是稳定的.上述分析结果与数值仿真结论一致，从理论上分析了谷值电流控制的H桥逆变器产生不稳定的原因.

4 结束语

笔者研究了谷值电流控制的H桥逆变器中的非线性动力学行为，建立了离散模型，运用频闪图、分岔图、折叠图及Lyapunov指数谱详细分析了该逆变器的非线性现象，从数理角度出发，采用Jacobian矩阵理论分析了逆变器稳定性发生变化的原因.研究结果表明：谷值电流控制的H桥逆变器的动力学演化过程具有典型的非线性特征，其稳定性受多个电路参数影响，逆变器稳定运行范围随输入电压E变化而变化，合理选择电路参数能提高逆变器的稳定性.研究结论对于谷值电流控制的H桥逆变器的设计具有指导意义.