椭圆曲线y2=x3+135x-278的整数点

崔保军

(甘肃民族师范学院 数学系,甘肃 合作 747000)

设N+是全体正整数的集合.近年来,寻找椭圆曲线整数点的问题引起了人们的关注,这方面的成果也有着广泛的应用[1-2].文献[3]提出了椭圆曲线

y2=x3+27x-62

(1)

的整数点问题.文献[4]运用代数数论的P-adic分析方法证明了椭圆曲线(1)仅有整数点(x,y)=(2,0)和(28 844 402,±154 914 585 540).文献[5]运用Pell方程和二元四次Diophantine方程的一些已知结果,给出了上述结论的一个简洁证明.文献[6]运用初等方法给出了式(1)的一种推广形式的整数点.论文运用同余、平方剩余等初等方法得出了定理.

定理椭圆曲线

y2=x3+135x-278

(2)

有整数点(x,y)=(2,0),(14,±66),(284 594,±151 823 364).

1 若干引理

引理1[7]若D是一个非平方的正整数,则Pell方程

u2-Dv2=1,u、v∈N+

(3)

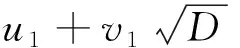
引理2[8]若D是一个非平方的正整数,则方程

X2-DY4=1,X,Y∈N+

(4)

至多有2组解(X,Y),而且恰有2组解的充要条件是D∈{1 785,28 560}或者2u1和v1都是平方数,其中(u1,v1)是(3)式的最小解.

引理3[10]当D=12时,方程y2=Dx4+1无正整数解.

引理4[11]方程3x4-y2=2仅有正整数解(x,y)=(1,1).

引理5方程

3(a2+1)2+46=b2

(5)

仅有整数解a=0,a=2和a=308.

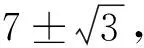
a2=7vn+un-1

(6)

或

a2=7vn-un-1.

(7)

易验证下列关系式成立

un+m=unum+3vnvm,

vn+m=umvn+vmun，

v2n=2unvn，

un+2rt≡(-1)tun(modur)，

vn+2rt≡(-1)tvn(modur).

对(6)式取模16,得剩余类序列周期为8,当n≡0,3,4,5,6,7(mod8)时，有7vn-un-1≡14， 14,6,12,12,6(mod16),但a2≡0,1,4,9(mod16)，故有n≡1,2(mod8).对(6)式取模7,其剩余类序列周期为8,当n≡2(mod8)时，有7vn-un-1≡6(mod8),但a2≡0,1,2,4(mod7)，故有n≡1(mod8). 令n=8m+1,有

a2=7v8m+1-u8m+1-1=7(u8m+2v8m)-(2u8m+3v8m)-1=5u8m+11v8m-1=

令d=gcd(2u4m+9v4m,u4m+v4m),则d|(u4m+v4m,7).又(u4m+v4m,7)=1,故d=1,有

2u4m+9v4m=2e2,u4m+v4m=f2,

其中：a=2ef,e，f∈Z.

由上式得

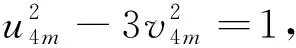
对(7)式,当n≡0(mod2)时,令n=2i,有

由于2⫮(3vi+7ui),(vi,3vi+7ui)=(vi,7ui)=1或7,由上式有

vi=2c2,3vi+7ui=d2,a=2cd,c,d∈Z.

(8)

vi=14c2,3vi+7ui=7d2,a=7cd,c,d∈Z.

(9)

对(7)式,如果n≡1,3(mod4),则un+7vn-1≡0,2(mod4).而a2≡0,1(mod4),故n≡1(mod4).当n≡0,1,2(mod3)时，有un+7vn-1≡0,3,4(mod5),因此n≡0,2(mod3).取模13,可得n≡0,3,5,10(mod12).综上仅需考虑n≡5(mod12).

当n≡5(mod12)时,令n=5+2·6s,此时

a2=7v5+2·6s+u5+2·6s-1≡±(u5+7v5)-1≡±1 825-1(modu6).

但193|u6,而

矛盾.引理得证.

2 定理的证明

设(x,y)是(2)式的解,从(2)式可得

y2=(x-2)(x2+2x+139).

(10)

因为x2+2x+139=(x+1)2+138>0,所以，从(10)式可知x≥2.当x=2时,由(10)式可知(2)式有整数点(x,y)=(2,0).因此,以下仅需考虑x>2且y≠0时的情况.

设d=gcd(x-2,x2+2x+139),易知d|147.故有d∈{1,3,7,21,49,147}.

以下分6种情况进行讨论：

(1) 当d=1时,从(10)式可知

x-2=a2,x2+2x+139=b2,y=±ab,gcd(a,b)=1,a,b∈N+.

(11)

从(11)式中第二个等式得(x+1)2+138=b2,知x+1≡b(mod2),但此时可得2≡b2-(x+1)2≡0(mod4)，矛盾.

(2) 当d=3时,从(10)式可知

x-2=3a2,x2+2x+139=3b2,y=±3ab,gcd(a,b)=1,a,b∈N+.

(12)

从(12)式可得3(a2+1)2+46=b2,由引理5知该方程仅有解a=0,a=2和a=308.故方程(2)有解(x,y)=(2,0),(14,±66),(284 594,±151 823 364).

(3) 当d=7时,从(10)式可知

x-2=7a2,x2+2x+139=7b2,y=±7ab,gcd(a,b)=1,a,b∈N+.

(13)

从(13)式可得

7a4+6a2+21=b2.

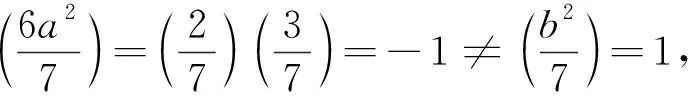
(4) 当d=21时,从(10)式可知

x-2=21a2,x2+2x+139=21b2,y=±21ab,gcd(a,b)=1,a,b∈N+.

(14)

从(14)式可得

21a4+6a2+7=b2.

同d=7的情况知,此时(14)式无解.

(5) 当d=49时,从(10)式可知

x-2=49a2,x2+2x+139=49b2,y=±49ab,gcd(a,b)=1,a,b∈N+.

(15)

从(15)式可得

3(a2+1)2+46a4=b2.

(16)

如果2⫮a,则从(16)式可知2|b,但此时有0≡b2≡3(a2+1)2+46a4≡2(mod4)，矛盾.

如果2|a,则从(16)式可知2⫮b,但此时有1≡b2≡3(a2+1)2+46a4≡3(mod4)，矛盾.

(6) 当d=147时,从(10)式可知

x-2=147a2,x2+2x+139=147b2,y=±147ab,gcd(a,b)=1,a,b∈N+.

(17)

从(17)式可得

(3a2+1)2+138a4=b2.

(18)

若2⫮a,则从(18)式可知2|b，但是从(16)式可得0≡b2≡(3a2+1)2+138a4≡2(mod4)，矛盾.

可知2|a.令

a=2e,e∈N+.

(19)

将(19)式代入(18)式可得

(12e2+1)2+2208e4=b2.

(20)

(21)

其中

s∈{2,6,16,46,48,138,368,1 104}.

(22)

以下按(22)式给出的8种情况进行讨论：

当s=2时,从(21)式可知

b=552f4+g4,12e2+1=552f4-g4.

(23)

从(23)式中第二个等式可知3⫮g,但此时可得1≡12c2+1≡552f4-g4≡-1(mod3).矛盾.

当s=6时,从(21)式可知

b=184f4+3g4,12e2+1=184f4-3g4.

(24)

从(24)式中第二个等式可知5⫮g.否则若5|g,则5|e,由gcd(f,g)=1知5⫮f.(24)式中第二个等式得1≡184f4≡4(mod5),矛盾.同理可知5⫮f.此时由于12e2+1≡3或4(mod5),而184f4-3g4≡1(mod5),知(24)式中第二个等式不成立.当s=16及s=46时,同s=6的情形可知此时(21)式均无解.

当s=48时,从(21)可知

b=23f4+24g4,12e2+1=23f4-24g4.

(25)

从(25)式中第二个等式可知3⫮f,但此时可得1≡12e2+1≡23f4-24g4≡2(mod3)，矛盾.

当s=138时,从(21)式可知

b=8f4+69g4,12e2+1=8f4-69g4.

(26)

从(26)式中第二个等式可知2⫮g,但此时可得1≡12e2+1≡8f4-69g4≡-1(mod4)，矛盾.

当s=1 104时,从(21)式可知

b=f4+552g4,12e2+1=f4-552g4.

(27)

从(27)式中第二个等式可得

(f2-6g2)2-588g4=1.

(28)

从(28)式可知

X2-588Y4=1

(29)

有解

(X,Y)=(|f2-6g2|,g).

(30)

因为方程

u2-588v2=1,u,v∈N+

(31)

的最小解(u,v)=(97,4),所以，根据引理2可得方程(29)至多有1组解(X,Y).比较(29)和(31)式：若(X,Y)是(29)式的解,则方程(31)必有解有(u,v)=(X,Y2).而根据引理1,从(31)式可得

(32)