载体行进间对准杆臂误差补偿算法*

王律化,石志勇,宋金龙,王海亮

(陆军工程大学石家庄校区，河北 石家庄 050003)

0 引言

装有惯性器件的载体在行进间完成初始对准时，理想情况是惯性器件和相应的辅助测量设备安装在载体中心。但是,由于载体的设计和使用的需求，惯性测量器件和相应的辅助设备一般不能安装在一起。同时,载体在行进间初始对准的过程中，由于载体自身的晃动和线运动，不在载体运动中心的惯性器件和辅助测量器件由于安装位置使得器件的测量值中含有杆臂误差。

针对上述问题，文献[1]分析了杆臂误差产生的机理，并运用线性卡尔曼滤波对于微幅晃动条件下的杆臂误差进行了补偿。高精度捷联惯导中，惯性测量器件不能等效为“点器件”[2-4]，因此，惯性器件内部也会存在杆臂误差，称为内杆臂误差。为此，文献[5-6]分析了惯性测量器件的内杆臂误差，得出内杆臂误差与加速度计距离3个加速度计敏感轴焦点的距离有关。当载体处在晃动条件下时，为了进一步提高对于载体杆臂误差的补偿，文献[7-9]提出了杆臂效应的力学补偿模型，但是由于安装误差和实际测量工具的原因[10-11]，使得在杆臂长度的确定中，存在不确定杆臂[12]，杆臂数值的准确测量变得十分困难。文献[13]根据晃动基座的对准原理，运用TRIAD(three-axis attitude determination)[14]双矢量定姿算法，给出了载体在晃动条件下确定杆臂长度，并利用杆臂效应的力学补偿算法对于杆臂误差进行在线补偿。当载体存在线运动条件时，由于载体自身晃动和线运动加速度的存在，使得按照上述方法解算杆臂长度存在困难。

为解决载体行进间杆臂误差的在线补偿问题，在分析杆臂误差产生的机理基础上，推导了基于里程计辅助条件下惯性系统自对准过程中解算杆臂长度的方法。同时，载体行进间对准的过程中，考虑到航向失准角为大角度，不能对于非线性的误差模型线性化，因此要采用非线性滤波的方法对于杆臂误差进行在线估计。本文在补偿算法上采用5阶CKF(cubature Kalman filter)非线性滤波算法进行在线补偿。仿真和实验结果表明，该方法可以很好地补偿由于杆臂所造成地行进间对准误差，提高初始对准精度。

1 杆臂误差机理

为说明杆臂效应对于惯性测量器件的影响，根据文献[1]杆臂效应的机理如图1所示。

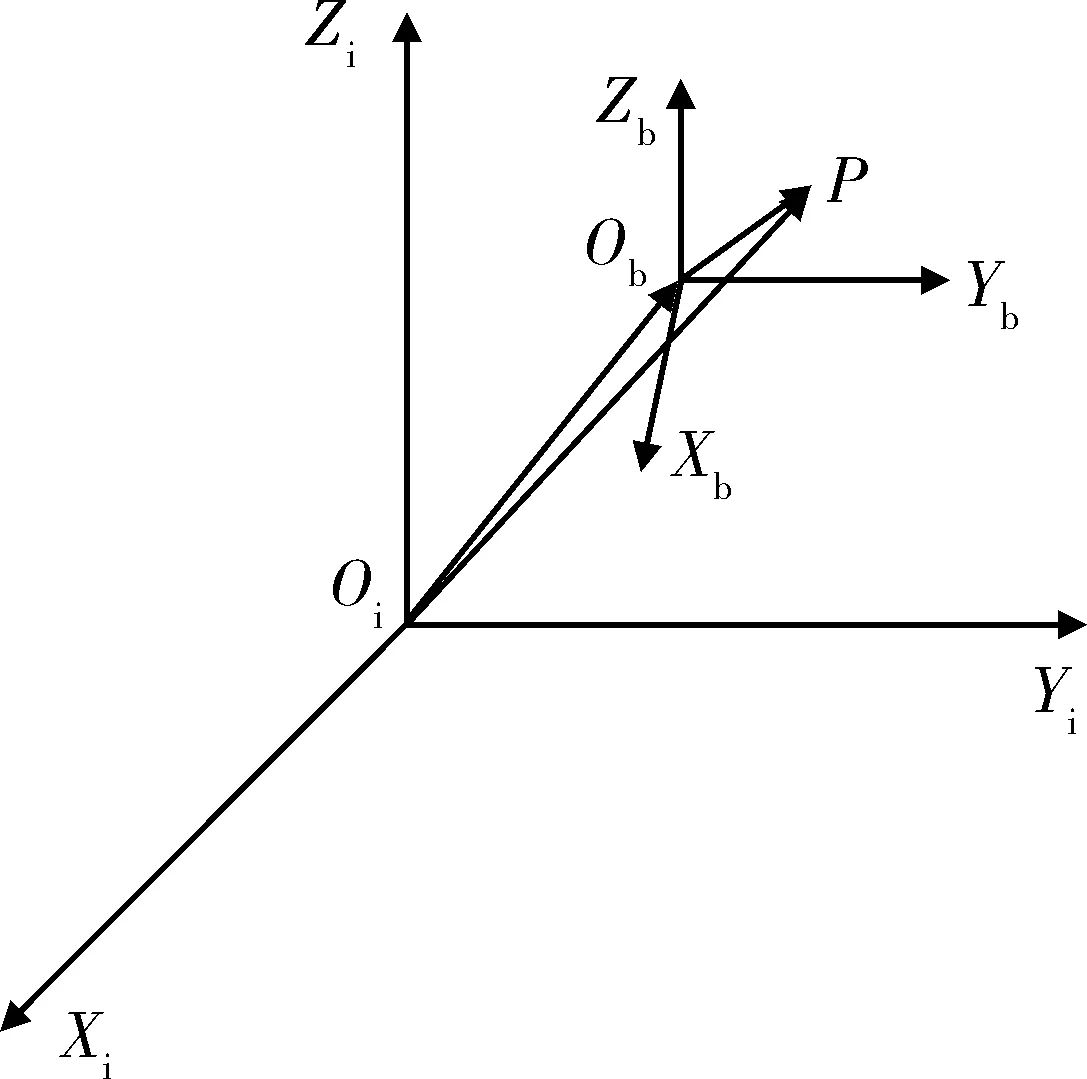
图1 杆臂效应原理图Fig.1 Principle of lever arm effect

图中，OiXiYiZi为惯性坐标系，ObXbYbZb为载体坐标系，加速度计安装于载体坐标系的P点处。载体坐标系相对于惯性坐标系存在晃动，晃动角速度为ωib，同时令OiOb=rb，OiP=RP，ObP=rP。

因此，杆臂误差可以表示为[1]

(1)

由于惯性器件固定在载体上，所以

因此，式(1)可以化简为

(2)

对于式(2)进行变形得

(3)

由式(3)可知，由于杆臂效应引起的加速度计的测量误差为

(4)

由式(4)可知，载体的杆臂误差主要和载体姿态变化的角速度有关。为了实现行进间杆臂效应的精确补偿，需要对于式(4)中的rp进行精确的测量。在此基础上，运用惯性导航系统提供的载体的转动角速度和角度，进行载体的力学补偿。

2 行进间杆臂误差的力学补偿

载体行进过程中，rp的准确测量成为实现杆臂误差力学补偿的关键。为保持载体的机动性，随时停车测量杆臂是不现实的，同时由于不确定性杆臂[12]的存在，使得杆臂长度的准确计算变得十分困难。

当载体处在运动状态下的时，根据文献[14]，载体的运动机械方程可以表示为

(5)

杆臂的力学误差δfb根据式(4)可以表示为

(6)

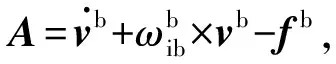
(7)

(8)

由于载体在初始对准的过程中运用速度为3～5 m/s，粗对准时的时间一般几十秒，相较于所计算的杆臂误差，可以忽略由于载体位置变化所引起的重力加速度的变化。将式(6)带入到式(7)，(8)中，并用两式作差，得

(9)

对于式(9)进行变形：

(10)

将式(10)计算得到的rp带入到式(6)中计算由于杆臂效应所引起的加速度误差。

3 非线性滤波模型建立

载体行进间杆臂效应误差的实时补偿，可以采用滤波的方法进行补偿。考虑到载体在行进过程中，粗对准结果航向失准角为大角度，应采用非线性差模型，并将杆臂所产生的误差项进行考虑。

(11)

式中:

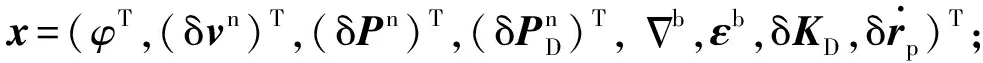
捷联惯导实测位置和里程计的实测位置的差值作为量测值

(12)

综上所述，行进间大方位失准角误差方程为

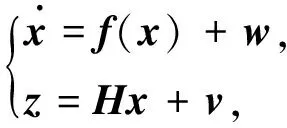
(13)

式中：f(x)的表达式具体看式(1)；噪声向量w和v是零均值，方差为Q和R的高斯白噪声。量测矩阵表示为

H=(03×3,03×3,I3×3,-I3×3,03×3,07×3)T.

4 非线性滤波模型解算方法

处理式(13)的滤波方法一般为贝叶斯滤波。将式(13)进行离散化处理表示为

(14)

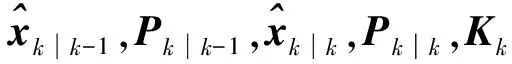
针对式(13)，可以采用贝叶斯估计[15]的方法进行解算，其解算过程中多涉及到如下形式的计算：

(15)

为了解算式(15)，根据文献[16]，高维积分的数值计算可以转化为

(16)

式中:ri和wr,i为径向积分的采样点和采样点对应的权值;sj和ws,j为球面积分的采样点和采样点对应的权值。I(h)的总采样地点为NrNs个，当ri中有一个采样点为0时，I(h)的总采样点数为(Nr-1)·(Ns+1)个。

4.1 5阶球面积分方法

形如IUn(hs)的积分，根据文献[17]，可以按照下列公式进行近似计算

(17)

式(17)为2m+1阶球面积分数值解算方法，式中IUn表示被解算的函数。式中的权值函数和采样点的函数值之和分别为

(18)

(19)

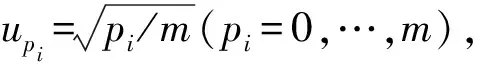
根据文献[16],有

(20)

式中：|k|=k1+k2+…+kn；Γ(z)为伽马函数，其定义为

。

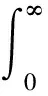
当所要近似的积分阶数是5阶的时候，2m+1=5，则m=2。将结果带入到式(18)中得

(21)

(22)

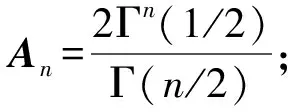
ws1所对应的采样点为

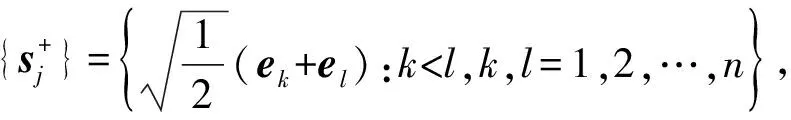
将式(21)和(22)以及采样点代入到式(17)中

(23)

4.2 径向积分法则

对于5阶及5阶以下的高维径向积分，可以使用高斯-拉格朗日积分方法，但是，这个方法不能运用于5维以上的数值解算。为提高径向高维积分解算方法的适用性，采用时矩匹配法解算径向积分。时矩匹配法具体表示为

(24)

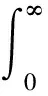
因此，当运用时矩匹配法解算5阶径向高维积分时，得到如下方程：

(25)

式中:Γ(z+1)=zΓ(z)。

由于式(25)中有4个未知数，只有3个方程，同时为了保证采用时矩匹配法数值解算径向积分的采样点数最少，可以令r1=0，于是求得式(25)的解为

(26)

将式(26)，(23)，(16)代入到式(15)中，运用5阶容积规则(Nr=2,Ns=2n2)解算得

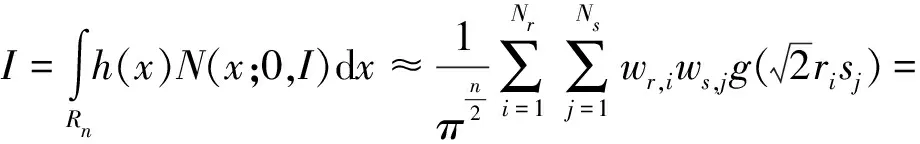
(27)

5 仿真和实验验证

为了充分验证采用力学方程和非线性误差方程结合对于行进间对准过程中对于杆臂长度的估计精度和在补偿杆臂误差后对准过程中位置的影响，通过仿真和实际实验的方法进行验证。

5.1 仿真条件

载体总的精对准仿真时间为400 s，假设载体的初始位置为34.245 1°N/108.908 4°E，高度0 m，陀螺为激光陀螺，其常值漂移为0.015 (°)/h，随机漂移为0.001 (°)/h，加速度计常值零偏为450 μg，随机漂移为10 μg，里程计的刻度系数误差为2‰，并且假设杆臂长度沿载体坐标3个方向的分别长度为：(0.45,0.28,0.57) m，载体在运动过程中的路径仿真如图2,3所示。

5.2 实验验证

通过图3杆臂在载体坐标系下仿真时间内的估计结果可以看出，在100 s以后，对于载体杆臂长度的估计趋于稳定。为表明载体杆臂对于对准精度的影响，通过无人车实际实验的方法验证对准过程中对于杆臂误差的补偿与否对于位置精度的影响。实验过程中，采用高精度差分GPS所测量的实时路线作为路径真值，GPS的输出为1 Hz，定位精度为1 m。通过2次实验对比补偿杆臂误差与否对于估计精度的影响实验结果如图4，5所示。

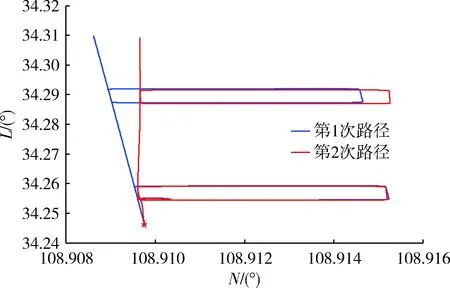
图2 路径仿真图Fig.2 Path simulation

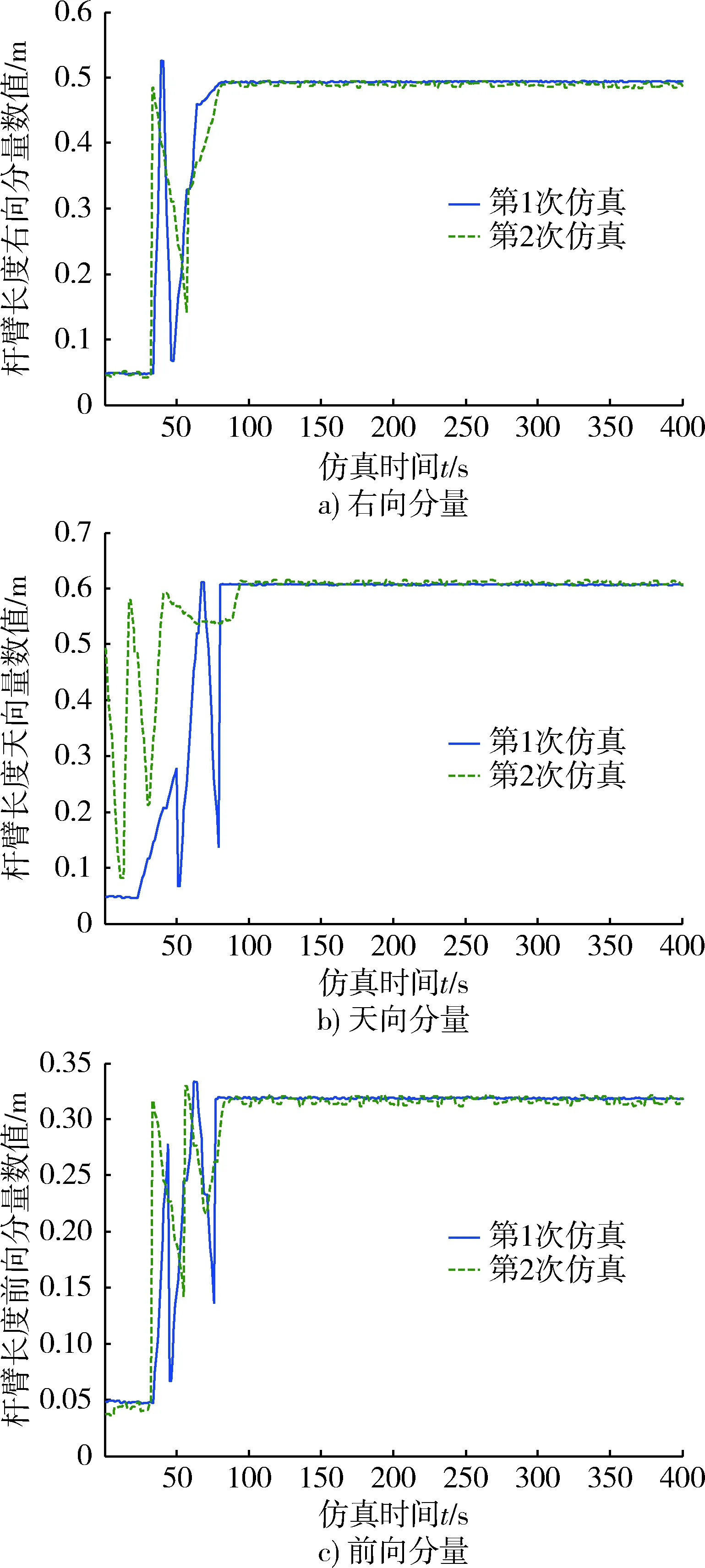
图3 杆臂长度在不同方向上的估计值Fig.3 Estimate of the arm length in different directions

图4 实验用无人车Fig.4 Experiment UGV

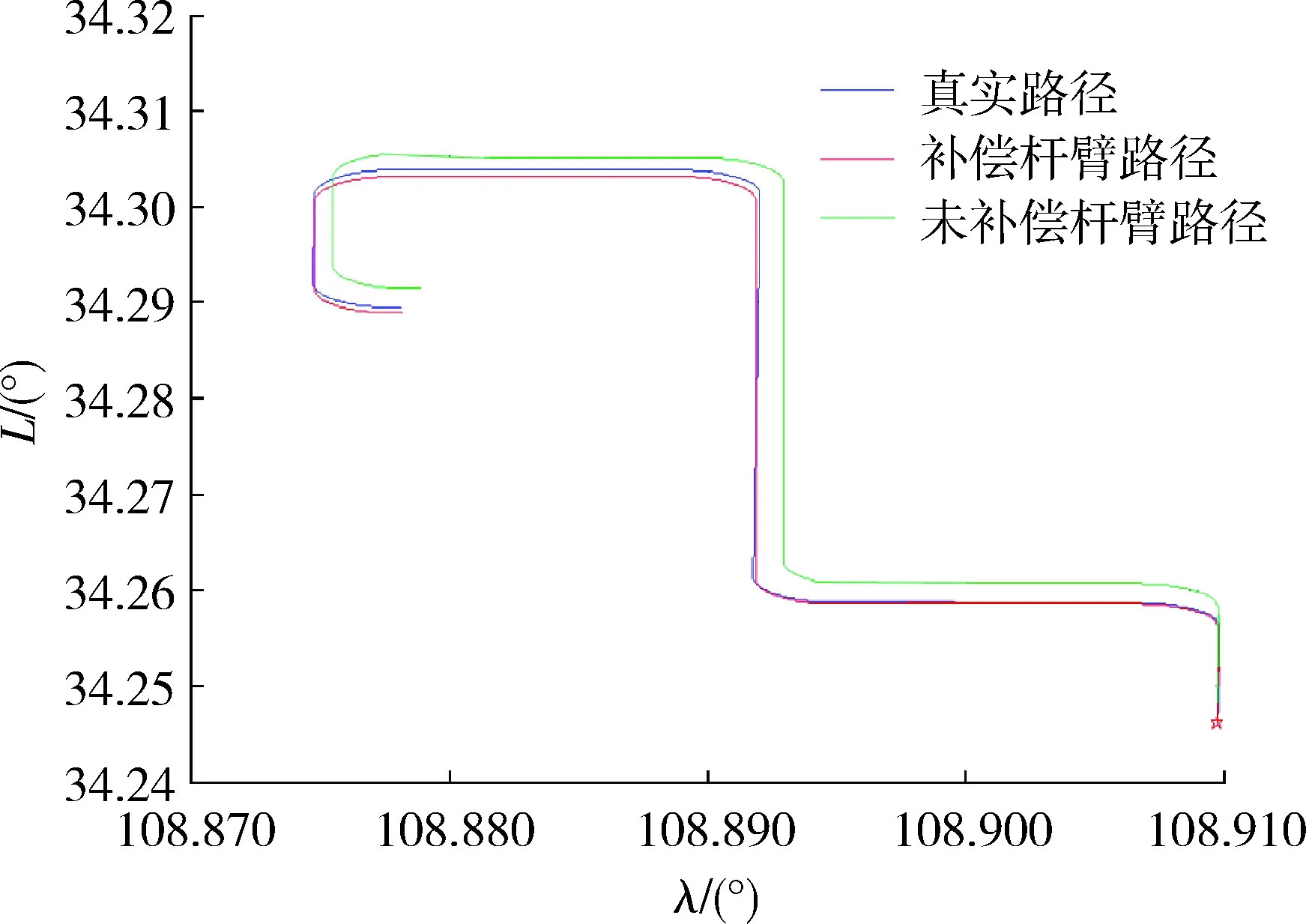
图5 实验路径图Fig.5 Experimental path

从以上图中不难看出，杆臂效应对于载体对准时位置估计精度的影响主要是在转弯运动时，当载体直线运动状态，即载体的姿态变化不大的情况下，杆臂效应对于载体定位误差的影响不大。

6 结束语

通过对于载体行进间对准过程中杆臂长度和误差补偿的仿真和实验表明：行进间对准过程中，对于载体杆臂误差主要受到载体姿态变化角速度的影响，采用5阶CKF滤波算法，将杆臂误差考虑到滤波的状态方程中，可以有效地提高载体在对准过程的定位精度，并且通过此算法，可以实现杆臂误差的实时补偿。